随着计算机图形图像处理能力的进步与发展, 人脸识别成为近年科研人员研究的热点之一, 人脸识别常用的技术方案有两种[1], 一种是基于人脸的全局特征进行识别, 能够有效的反映脸部特征的整体概况, 比较典型的方法有主成分分析(PCA)[2]、线性判别分析(LDA)[3]等. 另一种是基于人脸的局部特征进行识别, 侧重于体现脸部的细节信息, 比较典型的有局部二值模式(LBP)[4]、尺度不变特征变换(SIFT)[5]、梯度方向直方图(HOG)[6].
针对第二种方法, 研究人员做了大量的探索与改进, 文献[7,8]针对HOG算法进行了不同程度的改进, 在光照、旋转等方面取得较好的效果; 文献[9]将分块LBP应用于人脸识别中取得了良好的识别效果; 文献[10]提出一种通过提取MSF-VQ特征进行人脸识别的算法; 文献[11]提出一种通过改进加权稀疏进行人脸识别的算法; 文献[12]提出一种基于分块CBP特征和稀疏表示进行人脸识别的算法; 文献[13]提出完备局部二值模式(CLBP)人脸识别算法, 在LBP原基础上增加了局部差异值和中心像素灰度值的分析进行分类识别; 文献[14]提出基于最值平均人脸识别算法, 利用模板方差的大小选择不同的阈值, 提取更多细节信息; 文献[15]提出一种加权核主成分分析(WKPCA)的人脸识别算法, 通过将高、低分辨率人脸图像进行融合后, 形成新的特征进行识别; 文献[16]提出一种基于梯度脸(Gradient Faces, GF)的特征描述方法, 使用人脸的梯度信息进行特征提取, 对光照变化的人脸有较好的识别效果; 文献[17]提出一种基于中心对称梯度幅值相位模式(Center-Symmetric Gradient Magnitude and Phase patterns, CSGMP)的人脸识别算法, 该算法将人脸图像进行梯度变换后, 用CS-LDP算法进行特征提取, 取得了较好的识别效果.
上述算法都能很好的解决人脸识别的问题, 在识别率上有较好的改进与提升, 但在不同程度上存在算法复杂、耗时长等缺陷. 本文提出一种使用图像偏移产生多图像梯度, 对图像梯度进行变换产生若干个梯度算子, 使用梯度算子对原图像进行补偿融合, 然后进行特征提取的IGC (Image Gradient Compensation)算法, 实验结果表明该算法在识别率提升的同时, 其运行效率有非常卓越的表现.
1 基础理论 1.1 图像的梯度一维函数的一阶微分定义为:
| $\frac{{{\rm d}f}}{{{\rm d}x}} = \mathop {\lim }\limits_{\varepsilon - > 0} \frac{{f(x + \varepsilon ) - f(x)}}{\varepsilon }$ | (1) |
一张灰度图像, 将其认为成一个二维函数f(x,y), 分别对x、y求导即有:
| $\frac{{\partial f(x,y)}}{{\partial x}} = \mathop {\lim }\limits_{\varepsilon - > 0} \frac{{f(x + \varepsilon ,y) - f(x,y)}}{\varepsilon }$ | (2) |
| $\frac{{\partial f(x,y)}}{{\partial y}} = \mathop {\lim }\limits_{\varepsilon - > 0} \frac{{f(x,y + \varepsilon ) - f(x,y)}}{\varepsilon }$ | (3) |
因图像是离散的二维函数, ϵ不能无限小, 而图像是按照像素进行离散, 最小的ϵ就是1个像素. 因此, 对式(2)、式(3)化简, 产生式(4)、式(5) (ϵ=1):
| $\frac{{\partial f(x,y)}}{{\partial x}} = f(x + 1,y) - f(x,y) = gx$ | (4) |
| $\frac{{\partial f(x,y)}}{{\partial y}} = f(x,y + 1) - f(x,y) = gy$ | (5) |
式(4)、式(5)分别为图像中g(x, y)点的水平梯度(x方向)和垂直梯度(y方向), 从上面的表达式可以看出来, 当ϵ=1时, 图像的梯度相当于2个相邻像素之间的差值[18].
1.2 本文所涉及梯度概念的定义对于图像的一个像素点, 它在水平方向上有两个不同方向的梯度, 即左梯度、右梯度, 令Grx为水平方向的右梯度、Glx为水平方向的左梯度, 其计算公式分别为:
| $G_{rx} = \left| {f(x + 1,y) - f(x,y)} \right|$ | (6) |
| $G_{lx} = \left| {f(x,y) - f(x - 1,y)} \right|$ | (7) |
同理, 垂直方向上也有两个方向的梯度, 即上梯度、下梯度, 令Guy为垂直方向的上梯度、Gdy为垂直方向的下梯度, 其计算公式分别为:
| $G_{uy} = \left| {f(x,y - 1) - f(x,y)} \right|$ | (8) |
| $G_{dy} = \left| {f(x,y) - f(x,y - 1)} \right|$ | (9) |
水平方向上的左梯度与右梯度之和定义为图像A的水平合成梯度, 记做:
| $ {{{G}}_{{\rm{hor}}}}{\rm{ = }}{{{G}}_{{{rx}}}}{\rm{ + }}{{{G}}_{{{lx}}}} $ | (10) |
垂直方向上的上梯度与下梯度之和定义为图像的垂直合成梯度, 记做:
| $ {{{G}}_{{\rm{ver}}}}{{ = }}{{{G}}_{{{uy}}}}{\rm{ + }}{{{G}}_{{{dy}}}} $ | (11) |
水平方向上右梯度减左梯度的值定义为图像水平方向的差额梯度, 记做:
| $ {{{G}}_{{\rm{hs}}}}{\rm{ = }}{{{G}}_{{{rx}}}}{\rm{ - }}{{{G}}_{{{lx}}}} $ | (12) |
垂直方向上的上梯度减下梯度的值定义为图像垂直方向的差额梯度, 记做:
| $ {{{G}}_{{\rm{vs}}}}{\rm{ = }}{{{G}}_{{{uy}}}}{\rm{ - }}{{{G}}_{{{dy}}}} $ | (13) |
图像A的水平合成梯度与垂直合成梯度之和定义为图像A的合融梯度, 记做:
| $ {{{G}}_{{\rm{fusion}}}}{\rm{ = }}{{{G}}_{{\rm{hor}}}}{\rm{ + }}{{{G}}_{{\rm{ver}}}}{\rm{}} $ | (14) |
水平方向的差额梯度与垂直方向的差额梯度之和定义为图像A的差融梯度, 记做:
| $ {{{G}}_{{\rm{subfus}}}}{\rm{ = }}{{{G}}_{{\rm{hs}}}}{\rm{ + }}{{{G}}_{{\rm{vs}}}} $ | (15) |
为了获得可以更好描述图片的特征, 我们通过以下步骤逐步提取图片的特征信息:
(1) 将图片转换为灰度图img;
(2) 计算图片img上下左右4个方向上的偏移矩阵, 分别求出img在水平方向的左梯度、右梯度, 垂直方向的上梯度、下梯度, 填充对应矩阵, 使上述梯度矩阵与图片img的维度相同; 为了验证上述上、下、左、右梯度提取的图像信息, 对如图1(a)所示的包含正方形等形状的图片进行检测, 分别对其提取4个方向的梯度, 如图1(b)~图1(e)所示, 分析发现, 图像垂直方向的上、下梯度可以提取图片横向特征信息, 水平方向的左、右梯度可以提取纵向特征信息;
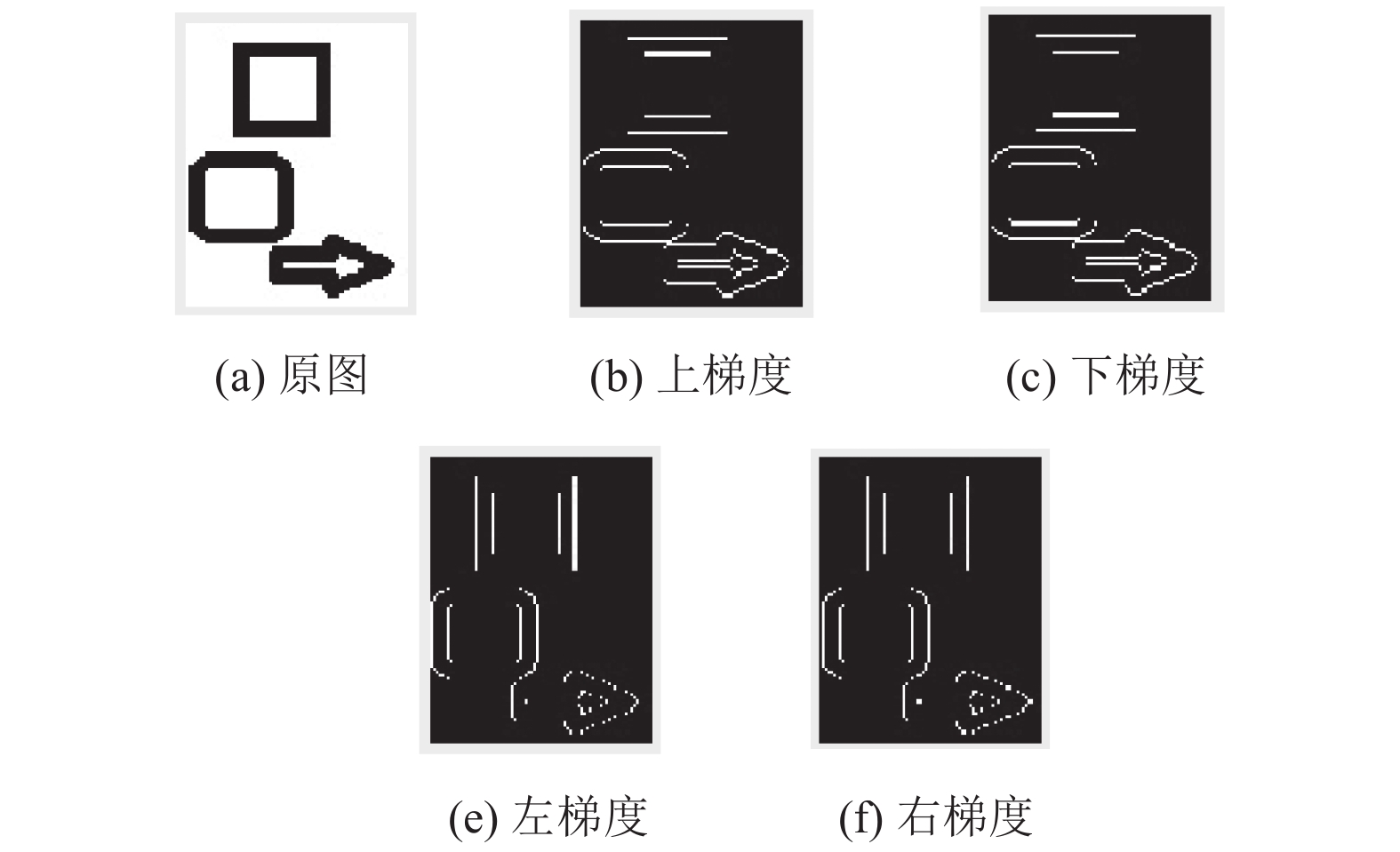
|
图 1 图形图像在各方向上的梯度图像 Fig. 1 graphic image in the sides of the upward gradient image |
(3) 获取图片img的水平合成梯度、垂直合成梯度;
(4) 合成图片的合融梯度Gfusion、差融梯度Gsubfus;
(5) 将合融梯度累加到图片img, 完成对img图像的补偿, 得到强化了图片轮廓信息的img2;
(6) 在img2的基础上, 减去若干次差融梯度Gsubfus, 完成对img图像的负补偿, 得到新的特征图片imgNew, 该图即为本文所述用于img图像特诊提取的特征图像.
2 图像梯度补偿IGC算法 2.1 算法流程首先通过IGC算法提取图片的特征, 其次, 参照文献[14]将图片按照3×3的模板分解为多个子图, 再次分别统计各子图的直方图, 形成特征向量, 然后用PCA进行降维, 最后使用SVM分类法对图片进行分类训练并做出识别, 本文算法所采用的流程如图2、图3所示.

|
图 2 IGC算法流程图 Fig. 2 IGC algorithm flow chart |
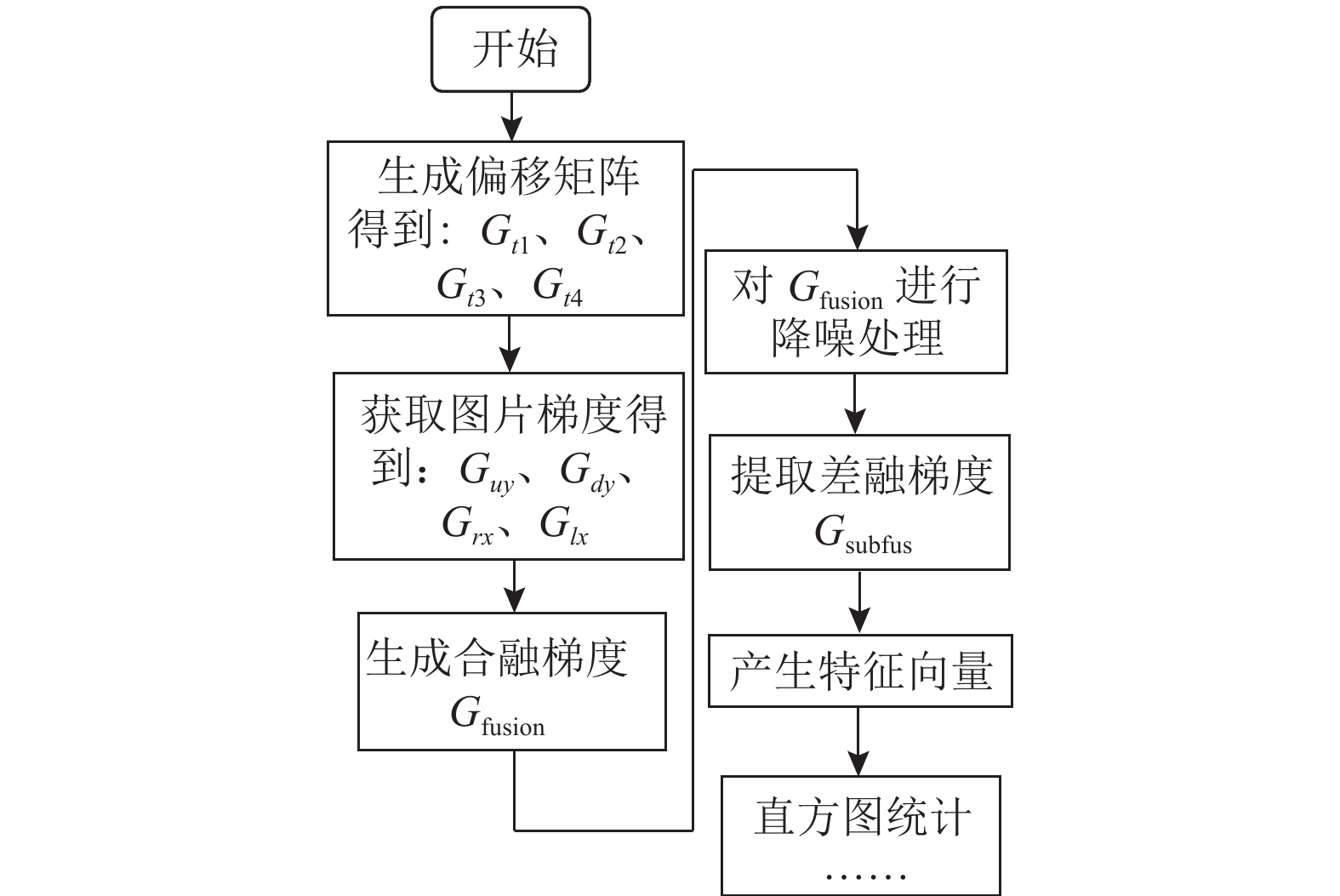
|
图 3 Lena图像的特征向量提取流程图 Fig. 3 Lena image feature vector extraction flow chart |
2.2 梯度补偿算法的实施
读取图片, 并将其转换为灰度图, 获得图片的m×n阶矩阵A.
Step 1. 生成偏移矩阵
将矩阵A的所有元素向Y轴正方向上移1位, 产生矩阵Gt1, 实现过程为:
令i<m、j<=n时, Gt1(i,j)等于矩阵A的第i+1行、第j列的数值, 即A(i+1,j); 令i=m、j<=n时, Gt1(i,j)的值等于Gt1(i–1,j), 得到一个与A同阶的m×n矩阵. 其实现公式为:
| ${{{G}}_{t1}}{\rm{(}}i,j) = \left\{ {\begin{array}{*{20}{l}} {A(i + 1,j),\;{i > = 1\& i < m\& j < = n} } \\ {{G_{t1}}(i - 1,j),\;{i = m\& j < = n} } \end{array}} \right.$ | (16) |
参照上述的方法, 分别取得Y轴负方向下移1位矩阵Gt2、X轴正方向左移1位矩阵Gt3、X轴负方向右移1位矩阵Gt4, 其实现公式分别为:
Gt2的实现公式:
| ${{{G}}_{t2}}{\rm{(}}i,j) = \left\{ {\begin{array}{*{20}{l}} {A(i - 1,j),\;i > 1\& i < = m\& j < = n} \\ {{G_{t2}}(i + 1,j),\;{i = 1\& j < = n} } \end{array}} \right.$ | (17) |
Gt3的实现公式:
| ${{{G}}_{t3}}{\rm{(}}i,j) = \left\{ {\begin{array}{*{20}{l}} {A(i,j - 1),\;{j > 1\& j < = n\& x < = m} } \\ {{G_{t3}}(i,j + 1),\;{j = 1\& x < = m} } \end{array}} \right.$ | (18) |
Gt4的实现公式:
| ${{{G}}_{t4}}{\rm{(}}i,j) = \left\{ {\begin{array}{*{20}{l}} {A(i,j + 1),\;{j > = 1\& j < n\& x < = m} } \\ {{G_{t4}}(i,j - 1),\;{j = n\& x < = m} } \end{array}} \right.$ | (19) |
Step 2. 获取图片梯度
为了提取图像中的轮廓信息, 我们令垂直方向上梯度Guy=|A–Gt1|, 此时, 如果矩阵A中的像素点g(i,j)与其上一行同列像素的值相同或者相近, 运算后Guy(i,j)的值为0或者一个非常小的数值, 如果g(i,j)与其上一行同列像素的值存在较大差距, 表明该像素点很有可能是图像的轮廓, 该值经过绝对值运算之后为正数, 能体现图像轮廓.
用上述方法获取Guy、Gdy、Grx、Glx几个方位的偏移差额图, 其计算公式分别为:
| $ {{{G}}_{{{uy}}}} = \left| {{{A}} - G{_{t1}}} \right| $ | (20) |
| $ {{{G}}_{{{dy}}}} = \left| {{{A}} - {G_{t2}}} \right| $ | (21) |
| $ {{{G}}_{{{rx}}}} = \left| {{{A}} - {G_{t3}}} \right| $ | (22) |
| $ {{{G}}_{{{lx}}}} = \left| {{{A}} - {G_{t4}}} \right| $ | (23) |
对Lena图像提取上述4个方向的梯度后, 其图像结果如图4所示.
Step 3. 提取合融梯度
将上述水平方向的左梯度、右梯度按照式(10)所示进行累加, 得到水平合成梯度Ghor, 将垂直方向的上梯度、下梯度按照式(11)所示进行累加, 得到垂直合成梯度Gver. 然后将Ghor、Gver进行累加, 得到矩阵合融矩阵Gfusion, 其实现过程如式(14)所示. 对Lena头像进行处理后的合融梯度Gfusion图像如图5所示.
Step 4. 对Gfusion进行降噪处理
上述过程所产生的Gfusion中存在较多的散点, 这些散点大多并非图片轮廓相关的特征信息, 为了剔除散点的影响, 我们使用适当算法对该矩阵进行降噪处理; 本文采用均值法, 其算法的实现公式为:
| ${{{G}}_{{\rm{fusion}}}}(i,j) = \left\{ {\begin{array}{*{20}{l}} {{{{G}}_{{\rm{fusion}}}}(i,j),\;{{{{G}}_{{\rm{fusion}}}}(i,j) > = mean}} \\ {0,\;{{{{G}}_{{\rm{fusion}}}}(i,j) < mean} } \end{array}} \right.$ | (24) |
其中,mean为矩阵Gfusion的像素点均值.

|
图 4 Lena图片各方向的梯度图像 Fig. 4 gradient image of each direction of Lena picture |

|
图 5 Lena的合融矩阵图像 Fig. 5 fusion matrix image of Lena |
为验证降噪的必要性, 在ORL数据库中分别验证了使用降噪前的Gfusion和使用降噪后的Gfusion对图片进行特征补偿, 然后提取图像的特征描述进行识别并计算识别率, 根据实验结果, 使用降噪前的Gfusion对图片进行特征补偿作为图片特征描述的识别率为87.5%, 而使用降噪后的Gfusion其识别率为88.75%, 即使用降噪后识别率提升了1.25%.
Step 5. 提取差融梯度
1)提取水平、垂直方向的差额梯度
使用式(12), 对垂直方向的上梯度Guy、下梯度Gdy进行相减, 得到矩阵Gvs, Gvs可以较好的保留纵向(Y轴)方向上更细微的局部特征; 使用式(13), 对水平方向的左梯度Grx、右梯度Glx相减, 得到矩阵Ghs, Ghs可以较好的保留横向(X轴)方向上更细微的局部特征.
2)提取图片的差融梯度
使用式(15)将上述所获得的两个差额矩阵Gvs、Ghs累加, 得到图像的差融梯度Gsubfus, 该矩阵可以描述图片水平、垂直方向上的更细微的特征信息, Gsubfus相对Gfusion而言, 提取的信息更加细腻, 而Gfusion的特征信息更加粗犷; Lena图像的差融矩阵Gsubfus图像如图6所示.
Step 6. 产生特征向量
1)使用Gfusion矩阵对矩阵A进行正补偿
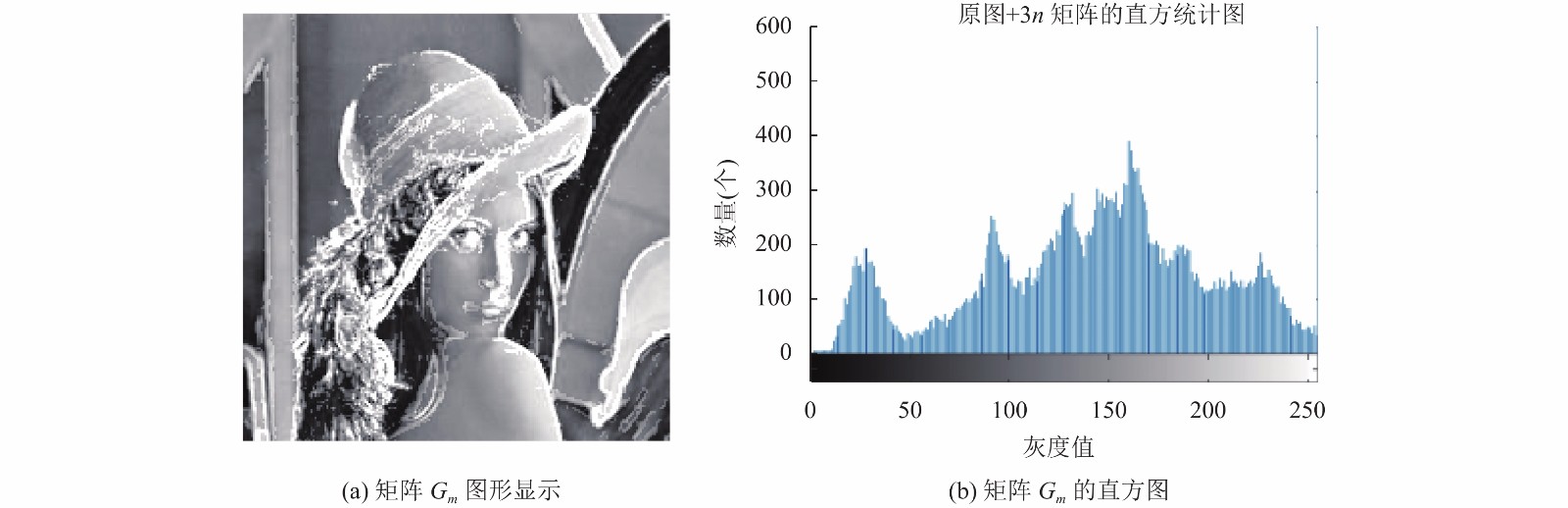
合融梯度Gfusion较好的提取了图片A的轮廓等特征信息, 但该图是否适合直接用作图片的特征值? 研究人员以图像Lena为例, 对Gfusion矩阵分析发现, 灰度值为0的像素点统计数为27357, 占比达到68.4%, 图片中大于等于均值的像素点个数为12643个, 因为图像像素值分布太不均匀, 直接用做图片特征值进行识别的话, 识别率不会很高; 实验证明, 直接使用该图片在ORL人脸数上的识别率为87.5%. 为了进一步提高图像识别率, 使用Gfusion矩阵对原灰度图矩阵A进行正补偿(即对应位置像素值相加), 获得新的矩阵Gm.
| $ {{{G}}_{{m}}}{{ = A + }}{{{G}}_{{\rm{fusion}}}} $ | (25) |
其图像显示及直方图分别如图7所示.

|
图 6 Lena图像的差融矩阵Gsubfus的图像显示 Fig. 6 shows the image of the difference fusion matrix Gsubfus of the Lena image |
|
图 7 Lena图像的Gm图像及其直方图 Fig. 7 Gm image of Lena image and its histogram |
矩阵Gm有以下3个特点: ① 像素点相对均衡; ② 强化了图片中能代表图片特性的轮廓特征; ③ 255像素点附近的数量增多, 这是因为在原矩阵A上正补偿了合融矩阵Gfusion, 导致图片轮廓附近的像素值达到最大值255, 从图片中的亮点可以看到.
因为对图片的训练、识别要用到直方图特性, 而255像素点附近的像素点数量增多, 会在一定程度上会降低图像的识别率, 为了进一步提高图片识别率, 需要通过一定途径进一步降低图像Gm中255像素点的数量.
2)使用Gsubfus对Gm进行负补偿
对比Step 4和Step 7的结果Gm和Gsubfus, 在Gm图像中, 有部分亮点的像素值超过255, 使用Gsubfus对Gm图像亮点部分的像素值进行适当的负补偿(即对应位置像素值的相减), 以增强图片的特征. 因Gm是由原图A叠加Gfusion而来, Gfusion体现的是图片粗狂的轮廓信息, 而Gsubfus能体现图片更细微的轮廓特征, 用Gsubfus对应位置的像素值来减弱Gm的亮点, 可以有效降低亮点的数量, 增强图片的可识别性. 我们令
| $ {{{G}}_{{\rm{fig}}}} = {{{G}}_{{m}}} - {{{G}}_{{\rm{subfus}}}}*{{r}} $ | (26) |
其中, r为补偿系数, 实验证明r取4~12范围内的数字时, 识别效果较好, 图8是r=7时对应的图片效果.

|
图 8 本文算法特征图 Fig. 8 feature graph of the algorithm in this paper |
矩阵Gfig即为本算法用于代表图片特征的最终矩阵, 该矩阵保留了原图更多的细节特征, 有利于图片的识别.
为了验证使用Gsubfus对Gm进行负补偿的有效性, 在ORL数据库中分别验证了使用Gsubfus对Gm进行补偿前和补偿后的识别率, 其他条件不变, 补偿前即直接使用Gm进行识别, 其识别率为88.75%; 使用补偿系数r=1对Gm进行负补偿之后, 其识别率为91.25%, r=2时, 识别率为93.75%. 实验表明, 使用Gsubfus对Gm进行负补偿, 可以有效地提高系统的识别率.
Step 7. 使用特定的模板对上述特征矩阵Gfig进行分块, 并对每个分块的图片进行直方图统计, 然后按照一定的次序将各个分块的直方图进行连接, 形成特征向量, 本文对特征图的分块采用3×3模式.
2.3 PCA降维经过上述IGC算法所获取的特征向量维度较高, 可以达到1000维以上, 过高的维数不利于提高图片的识别效果, 另外, 特征向量的维数越高, 在进行模型训练及识别时, 需要耗费更多的时间及存储资源, 为此, 采用PCA技术对特征向量进行降维处理; PCA主成分分析算法是最常用的降维手段之一[19], 可以有效的降低高维数据并获取最主要的特征信息, PCA就是从原始的空间中顺序地找一组相互正交的坐标轴, 以此找出与原始数据或者坐标轴方差最大的坐标轴, 直到找出n个这样的坐标轴, 其中前k个坐标轴包含了大部分方差, 后面的坐标轴所含的方差几乎为0, PCA提取前k个坐标轴作为特征向量, 从而实现了对高维向量进行降维的目的.
2.4 SVM向量机支持向量机方法是以统计学理论为基础, 通过对有限样本信息的提炼, 从而产生一个可以对其他测试样本进行判别、分类的工具, SVM有很多优点, 如基于结构风险最小化, 克服了传统方法的过学习(overfitting)和陷入局部最小的问题, 具有很强的泛化能力[20]; 采用核函数方法, 向高维空间映射时并不增加计算的复杂性, 又有效地克服了维数灾难(curse of dimensionality)问题. 基于以上各方面的优势, SVM分类算法在人脸识别领域获得了非常广泛的使用[21]. 本文采用的SVM模型为文献[22]中的LIBSVM软件包, 用在Matlab 2016 a上进行人脸识别分类实验.
3 实验与结果分析 3.1 实验环境本文试验操作平台硬件配置CPU为四核i3-2370M, 主频2.4 GHz, 内存8 GB (其中显存分配1 GB), Win7旗舰版64位操作系统, 开发软件选用Matlab 2016a, 实验数据使用ORL和CMU_PIE人脸数据库完成测试.
3.2 相关参数设置 3.2.1 补偿系数r在式(26)中, 补偿系数r的取值, 会在一定程度上影响算法识别的准确率, 为了得到更合理的取值, 对r取不同数值时对测试结果的影响进行对比, 其结果如表1所示.
| 表 1 不同补偿系数r在各个数据库上的识别率(%) Table 1 recognition rates of different compensation coefficient r on each database % |
分析实验结果表明, r的值过大或者过小, 都会对识别率造成一定的影响, 较合理的取值范围在4–12之间. 这是因为: r值过小, 强化了特征补偿原图的亮点数量减少的不够, 不足以形成一个新的特征; r值过大, 会使得被强化了特部分特征点的值太小, 甚至为0, 对图像的最终识别产生一定的影响.
3.2.2 其他参数设置图片分块模板采用3×3的模板, 然后对各个子图进行直方图统计; 分类器使用文献[22]开发的LIBSVM分类器, 其对应参数设置为“–s 0 –t 2 –c 1.4157 –g 0.00375”.
3.3 实验结果为了分析本文算法的效果, 在不同的数据库上, 分别将经典LBP、文献[13]、文献[14]、文献[15]等几个算法与本文算法进行对比, 实验流程为, 先提取特征图片, 次对特征图进行分块, 再统计各子图的直方图后串联, 然后进行PCA降维, 最后使用LIBSVM分类器进行识别并计算识别率; 各对比算法按照引用文献所提供的参数进行设置.
3.3.1 ORL数据库ORL由40个人, 每人10张在不同光照、不同角度的情况下进行摆拍, 共计400张人脸图组成, 其图片采用92×112规格的灰度图像, 使用每人的前8张图片进行训练, 后2张图片用于测试.
由表2分析可知, 在ORL人脸数据库中, 经典LBP算法识别率为92.5%, 文献[13]算法为86.25%, 文献[14]识别率为80%, 文献[15]识别率为98.75%, 本文算法的识别率为98.75%, 即除文献[15]之外, 本文算法在上述环境下的识别率均高于其他算法, 与文献[15]所述算法的识别率持平.
| 表 2 ORL数据库实验结果数据结果(%) Table 2 experimental results of ORL database data results |
3.3.2 CMU_PIE数据库
CMU_PIE数据库由68个人, 每人24幅不同光照、不同角度情况下进行摆拍的图片组成, 共计1632张人脸图组成, 其图片采用64×64规格的灰度图像, 使用每人的20张图片进行训练, 其余图片用于测试样本.
由表3分析可知, 在CMU_PIE人脸数据库中, 经典LBP、文献[13]、文献[14]、文献[15]的识别率分别是82.35%、97.426%、90.75%、61.40%, 本文算法的识别率为91.54%, 在CMU_PIE数据库中, 文献[13]表现出较好的识别率, 其算法的识别率高于本文算法6.886个百分点, 文献[14]的表现也不错, 可达到90.75%, 而本文算法识别率为91.54%, 超过了除文献[13]算法之外的其他算法.
| 表 3 CMU_PIE实验结果数据结果(%) Table 3 data results of CMU PIE experiment /% |
为了进一步对比各个算法的综合表现, 我们将上述算法在ORL、CMU_PIE数据库上的识别率求平均值, 其结果如表4所示, 分析表4可知, 综合两个数据库的表现, 虽然文献[15]在ORL数据库中的识别率与本文所述算法持平、文献[13]所述算法在CMU_PIE数据库的人脸识别率上比本文算法表现更好, 但是, 综合两个数据库的结果, 本文算法的综合表现要优于上述文献的算法.
| 表 4 ORL与CMU_PIE人脸库综合对比(%) Table 4 comprehensive comparison between ORL and CMU PIE face library /% |
3.3.3 时间复杂度分析
为了对比不同算法的计算效率, 使用Matlab软件的计时功能, 分别记录了经典LBP算法、文献[13]、文献[14]、文献[15]算法及本文算法从提取特征值开始到提取结束所消耗的总时长, 其结果如表5所示.
| 表 5 实验结果耗时数据分析(单位: s) Table 5 data analysis of experimental results |
分析表5可知, 在ORL数据库中, 文献[15]提取特征值所消耗的时间最短, 为7.9852 s, 除文献[15]之外, 本文算法在运行耗时方面低于其他算法, 提取特征速度是文献[13]算法的1.75倍, 是经典LBP算法的4.14倍, 同时也远远高于其他算法的运行速度; 在CMU_PIE数据库中, 在ORL数据库中表现优异的文献[15]算法, 耗时为86.853, 该值为研究者多次反复求证的结果, 与ORL数据库中提取特征信息运行效率的表现差别较大. 本文算法耗时仅为17.109 s, 此外, 在除本文算法之外的其他算法中, 文献[13]算法用时最短为61.679 s, 是本文的3.61倍. 综合两个数据库的平均耗时, 本文算法为13.815 s, 远远高于其他算法的运行时间.
4 结语本文提出一种基于图像梯度变换产生若干梯度算子, 使用梯度算子与原图像融合进行特征提取的人脸描述与识别算法. 仿真实验结果表明, 本文所提的IGC图像梯度补偿算法在ORL和CMU_PIE人脸数据库上取得较高识别率, 其运行效率具有非常卓越的表现, 同时算法具有较强的人脸特征描述功能, 对光照、人脸表情和位置的变化具有较高的鲁棒性.
| [1] |
万源, 李欢欢, 吴克风, 等. LBP和HOG的分层特征融合的人脸识别. 计算机辅助设计与图形学学报, 2015, 27(4): 640-650. |
| [2] |
Bartlett MS, Movellan JR, Sejnowski TJ. Face recognition by independent component analysis. IEEE Transactions on Neural Networks, 2002, 13(6): 1450-1464. DOI:10.1109/TNN.2002.804287 |
| [3] |
Belhumeur PN, Hespanha JP, Kriegman DJ. Eigenfaces vs. Fisherfaces: Recognition using class specific linear projection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(7): 711-720. DOI:10.1109/34.598228 |
| [4] |
Ojala T, Pietikäinen M, Harwood D. A comparative study of texture measures with classification based on featured distributions. Pattern Recognition, 1996, 29(1): 51-59. DOI:10.1016/0031-3203(95)00067-4 |
| [5] |
Lowe DG. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision, 2004, 60(2): 91-110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [6] |
Dalal N, Triggs B. Histograms of oriented gradients for human detection. Proceedings of 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego, CA, USA. 2005. 886–893.
|
| [7] |
杨超, 伍世虔, 方红萍. 基于Fechner定律和梯度特征的人脸识别算法及实现. 计算机应用与软件, 2019, 36(1): 227-231. |
| [8] |
蒋政, 程春玲. 基于Haar特性的改进HOG的人脸特征提取算法. 计算机科学, 2017, 44(1): 303-307. |
| [9] |
黄金钰, 张会林, 闫日亮. LBP直方图与PCA的欧式距离的人脸识别. 计算机系统应用, 2012, 21(6): 202-204, 198. |
| [10] |
魏陆奇, 廉东本. 改进的MSF-VQ人脸特征提取方法. 计算机系统应用, 2018, 27(3): 283-287. DOI:10.15888/j.cnki.csa.006264 |
| [11] |
王林, 邓芳娟. 改进的加权稀疏表示人脸识别算法. 计算机系统应用, 2018, 27(6): 134-139. DOI:10.15888/j.cnki.csa.006385 |
| [12] |
马杰, 蔡轶珩, 盛楠. 基于分块CBP特征和稀疏表示的三维人脸表情识别. 计算机系统应用, 2019, 28(2): 196-200. DOI:10.15888/j.cnki.csa.006692 |
| [13] |
王宪, 张彦, 慕鑫, 等. 基于改进的LBP人脸识别算法. 光电工程, 2012, 39(7): 109-114. |
| [14] |
付波, 徐超, 赵熙临, 等. 基于最值平均的人脸识别LBP算法. 计算机应用与软件, 2019, 36(9): 209-213. |
| [15] |
李魁英, 赖惠成. 基于加权KPCA和融合极限学习机的人脸识别. 现代电子技术, 2019, 42(11): 36-39, 44. |
| [16] |
Zhang TP, Tang YY, Fang B, et al. Face recognition under varying illumination using gradientfaces. IEEE Transactions on Image Processing, 2009, 18(11): 2599-2606. DOI:10.1109/TIP.2009.2028255 |
| [17] |
杨恢先, 翟云龙, 蔡勇勇, 等. 基于中心对称梯度幅值相位模式的单样本人脸识别. 光电子·激光, 2015, 26(5): 969-977. |
| [18] |
杨朝霞, 逯峰, 李岳生. 图像梯度与散度计算及在边缘提取中的应用. 中山大学学报(自然科学版), 2002, 41(6): 6-9. |
| [19] |
张蓓, 王顺芳. 基于MCD稳健估计的PCA人脸识别算法. 计算机工程与设计, 2015, 36(3): 778-782. |
| [20] |
梁路宏, 艾海舟, 徐光祐, 等. 人脸检测研究综述. 计算机学报, 2002, 25(5): 449-458. |
| [21] |
高攀. 基于改进LBP算子的图像纹理分类研究[硕士学位论文]. 成都: 西南交通大学, 2018.
|
| [22] |
Chang CC, Lin CJ. LIBSVM: A library for support vector machines. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): 1-27. |
 2020, Vol. 29
2020, Vol. 29



