随着大数据时代的到来, 数据资源呈现出快速增长的趋势, 数据的存储容量也随之不断增加. 传统的数据存储系统已经不能适应当前海量数据存储, 分布式存储系统逐渐成为主流存储方式. 通过将海量数据分散的存储在多台互相独立物理设备上, 分布式存储系统不仅很好的分担了存储负载, 而且成本低廉, 可扩展性能好, 但是分布式存储系统中的这些物理存储设备容易发生故障, 可造成大量数据丢失. 因此, 如何提高数据存储的可靠性就成为了分布式存储亟需解决的问题^[1-3].

为保证数据存储时的高可靠性和高可用性, 传统的分布式存储系统中生成冗余数据的策略通常有“复制”和“纠删码”策略^[4,5]. 谷歌文件系统和Hadoop系统运用了三副本复制策略, 将原始数据块复制成三个副本然后存储在系统中来保证存储的可靠性, 这样会导致存储开销过大; 为了减小存储开销, 在实际系统中引入纠删码的冗余策略, 但该策略在修复故障节点时会带来巨大的带宽开销. 针对上述问题, Dimakis等将网络编码的思想运用到分布式存储中, 提出了再生码的概念^[6], 有效减少了存储开销和修复带宽开销. 目前对再生码的研究表明, 主要表现在存储和带宽均衡曲线上的两个极值点, 一个极值点对应最小存储再生码MSRC (Minimum Storage Regenerating Code), 另一个极值点对应最小带宽再生码MBRC (Minimum Bandwidth Regenerating Code). 文献[7-9]给出了一些好的再生码的构造方法.

但是, 再生码的缺陷在于, 在进行故障节点修复时, 需要大量基于有限域上的计算, 计算复杂度高, 修复局部性复杂. 为解决上述问题, EI Rouayheb和Ram chan dram在MBRC的研究基础上提出了一种新型码——部分重复码(Fractional Repetition Codes, FRC)^[10], 该码可以进行精确无编码有效的修复. 一般意义上的FRC由两部分组成: 外部的编码是最大距离可分码 (Maximum Distance Sparable, MDS)和内部是重复码, 该码修复故障节点无需任何编码操作, 可以很好地降低故障修复时所需的带宽和磁盘I/O开销. 目前对FRC的研究主要有基于组合设计构造的FRC^[11], 基于图构造的FRC^[12], 基于偏序集构造的FRC^[13], 基于二分图构造的局部修复的FRC^[14], 这些构造算法复杂, 并且大多只能构造同构的FRC, 不能得到异构的FRC.

为此, 本文提出了两种构造方法, 一种是基于矩阵变换构造的异构FRC, 该构造用于构造重复度为2, 节点存储容量异构的FRC, 该方法计算复杂度低, 只需进行简单的异或运算就可得到节点存储容量异构的FRC, 相比现有的运用正则图构造的同构FRC, 该构造在节点存储容量上更符合现实的存储系统; 另外, 本文还提出了运用可调节环构造的FRC, 该方法根据一定的存放规则能得到不同重复度的FRC, 主要构造重复度 的情况, 因为大部分对部分重复码的研究中重复度都是2或3, 同时该方法也可灵活的调节节点存储容量, 即可得到节点存储容量同构的FRC也可得到节点存储容量异构的FRC, 可大范围选择参数, 构造结构简单直观. 同时本文上最大的应用价值在于能无编码的修复节点存储容量异构的分布式存储系统中的故障节点, 应用前景好, 具有很好的实用价值.

1 基础知识

目前研究表明, 对MDS码的研究已经十分成熟了, 各种参数的MDS码都可得到. 所以对部分重复码的研究主要体现在内部重复码的构造上. FRC实际上是复制倍数为 $\rho $ 的 $\theta $ 个数据块在节点上的一种排列组合, 复制生成的数据块都分别存储在不同的系统节点上. 内部的重复码可用 $(n,k,d,\theta ,\rho ,\alpha )$ FRC表示, 其中n表示存储系统的节点数, $\theta $ 表示存储在节点中的数据块个数, $\rho $ 表示数据块的复制次数, $\alpha $ 表示每个节点的存储容量, $d$ 表示修复一个失效节点需连接的存活节点数, 一般认为 $\alpha = d$ . 数学上的定义如下:

定义1^[15]. 参数为 $(n,k,d)$ 分布式存储系统的部分重复码 $C = (M,U)$ , 复制倍数为 $\rho $ , 是指特定的n个子集的集合 $U = \{ {U_1},{U_2},\cdots,{U_n}\}$ , 每个子集的元素均来自于符号集 $M = \{ 1,2,\cdots,\theta \}$ . 并且节点存储容量同构的FRC还需要满足下面条件:

1)每个子集的大小均为d;

2) M中的每一个元素都属于U中的子集, 每个子集数大小为 $\rho $ ;

3)同构的FRC满足 $n\alpha = \rho \theta $ .

定义2^[16]. $({d_1},{d_2},\cdots,{d_m})$ 正则图 $G(V,E)$ 是一个无向图, 其中 $\left| V \right| = n$ , ${V_1},{V_2},\cdots,{V_m} \subset V$ , 并且 $\displaystyle\sum\nolimits_{i = 1}^\theta {\left| {{V_i}} \right|} = n, {V_i} \cap {V_j} = \emptyset $ . 顶点 ${V_i}$ 的度为 ${d_i}$ $(1 \le i \le m)$ , 若 $G(V,E)$ 所有顶点的度都等于 $d$ , 则该 $G(V,E)$ 叫作 $d$ -正则图, 若 $G(V,E)$ 顶点的度不相等分别为 ${d_1},{d_2},\cdots,{d_m}$ , 则称该 $G(V,E)$ 为 $({d_1},{d_2},\cdots,{d_m})$ -正则图, 也叫部分正则图.

2 基于矩阵变换的异构部分重复码构造

本节运用矩阵变换的思想, 结合部分正则图提出了一种新的节点存储容量异构的部分重复码, 相比文献[10]和文献[16]中运用正则图和部分正则图构造的部分重复码, 本构造能得到节点存储容量更加多样的FRC, 和传统RS码相比, 在修复单节点故障时, 修复局部性更好, 修复复杂度更优, 无需任何编码操作, 计算复杂低. 具体构造算法如下:

该构造主要用于构造节点存储容量异构的FRC, 适用于分布式存储系统节点数n为奇数的情况, 且构造的FRC中数据块的重复度 $\rho $ 等于2; 具体步骤如下:

步骤1. 定义一个 $n$ 阶的二进制循环置换矩阵 ${C_n}\left( {d - 1} \right)$ , 其中 $n$ 代表节点数, $d - 1$ 表示每个节点存储容量同时也表示矩阵中每一行1的个数, 且需满足的条件为 $d > 3$ , $d$ 为奇数; 同时我们设定 ${C_n}\left( {d - 1} \right)$ 矩阵的第一行在数学上满足的表达式为: $c\left( t \right) = t + {t^2} + \cdot \cdot \cdot + {t^{(d - 1)/2}} + {t^{n - (d - 1)/2}} + \cdot \cdot \cdot + {t^{n - 1}}$ .

在矩阵的第一行确定后, 矩阵后面的每一行依次向右移动一位, 共移动 $n - 1$ 次, 最后生成 ${C_n}\left( {d - 1} \right)$ 矩阵;

步骤2. 为得到节点存储容量异构的FRC, 在步骤1的基础上引入矩阵 ${S_n}$ 去调节步骤1中的 ${C_n}\left( {d - 1} \right)$ 矩阵, ${S_n}$ 矩阵生成方法为: 在 $(n - 1)$ 阶副对角线都为1, 其他元素全为0的方阵后面加一行0和一列0, 生成 $n \times n$ 阶的 ${S_n}$ 矩阵;

步骤3. 将步骤1中的矩阵 ${C_n}\left( {d - 1} \right)$ 和步骤2中的矩阵 ${S_n}$ 进行模2运算, 得到二进制矩阵 $P = {C_n}\left( {d - 1} \right) + {S_n}$ $({\rm{mod}}\; 2)$ , 矩阵 $P$ 和部分正则图存在相关联的关系, 用 $P = {({m_{ij}})_{n \times n}},\;1 \le i,j \le n$ 表示部分正则图的关联矩阵, 关联规则如下:

${m_{ij}}{\rm{ = }}\left\{ {\begin{array}{*{20}{l}} 1,&{{\text{图中第}}i{\text{顶点与第}}j{\text{个顶点相连}}}\\ 0,&{{\text{顶点}}i{\text{和}}j{\text{不相连}}} \end{array}} \right.$

由上面关系可知, 部分正则图的每一个顶点的度和矩阵的每一行中1的个数是相等的, 经过算法的验证, 发现矩阵 $P$ 的不同行中会出现有 $d,d - 1,d - 2$ 个1的情况, 因此对应的部分正则图的度有 $d,d - 1,d - 2$ 三种情况, 记作 $(d,d - 1,d - 2)$ -部分正则图, 也就对应着构造的FRC的节点存储容量有 $d,d - 1,d - 2$ 三种情况.

对构造的FRC的故障节点修复进行分析可知, 因为该FRC的重复度 $\rho = 2$ , 所以本构造能容忍单个节点出现故障, 又由于异构FRC的节点容量有 $d,d - 1,d - 2$ 三种情况, 所以分以下3种情况讨论:

1) 若存储容量为 $d$ 的节点出现故障, 那么只需要从另外的 $d$ 个节点分别下载一个数据块即可直接修复;

2) 若存储容量为 $d - 1$ 的节点出现故障, 那么只需要从另外的 $d - 1$ 个节点分别下载一个数据块即可直接修复;

3) 若存储容量为 $d - 2$ 的节点出现故障, 那么只需要从另外的 $d - 2$ 个节点分别下载一个数据块即可直接修复.

当系统中出现故障节点, 只需直接从其他存活的节点下载数据块修复, 修复选择性高, 无编码操作, 计算复杂度低. 根据上述构造算法给出如下具体实例.

例1. 给定 $n = 7,d = 5$ , 根据构造方法步骤1得到矩阵 ${C_7}\left( 4 \right)$ , 其中 ${C_7}\left( 4 \right)$ 是一个 $7 \times 7$ 的二进制矩阵且第一行表示为 $c\left( t \right) = t + {t^2} + {t^5} + {t^6}$ , 第一行确定后, 后面的每一行依次向右移动一位, 最后生成 ${C_7}\left( 4 \right)$ 矩阵, 如下所示:

${C_7}(4) = \left( {\begin{array}{*{20}{c}} { 0}&{1}&{1}&{0}&{0}&{1}&{1} \\ { 1}&{0}&{1}&{1}&{0}&{0}&{1} \\ { 1}&{1}&{0}&{1}&{1}&{0}&{0} \\ { 0}&{1}&{1}&{0}&{1}&{1}&{0} \\ { 0}&{0}&{1}&{1}&{0}&{1}&{1} \\ { 1}&{0}&{0}&{1}&{1}&{0}&{1} \\ { 1}&{1}&{0}&{0}&{1}&{1}&{0} \end{array}} \right)$

进一步运用矩阵 ${S_7}$ 调节矩阵 ${C_7}\left( 4 \right)$ , ${S_7}$ 矩阵是在6阶副对角线都为1, 其他元素全为0的矩阵后面加一行0和一列0生成的, 如下所示:

${S_7} = \left( {\begin{array}{*{20}{c}} { 0}&{0}&{0}&{0}&{0}&{1}&{0} \\ { 0}&{0}&{0}&{0}&{1}&{0}&{0} \\ { 0}&{0}&{0}&{1}&{0}&{0}&{0} \\ { 0}&{0}&{1}&{0}&{0}&{0}&{0} \\ { 0}&{1}&{0}&{0}&{0}&{0}&{0} \\ { 1}&{0}&{0}&{0}&{0}&{0}&{0} \\ { 0}&{0}&{0}&{0}&{0}&{0}&{0} \end{array}} \right)$

得到 ${S_7}$ 矩阵后, 通过 $P = {C_7}(4) + {S_7}$ $({\rm{mod}}\; 2)$ 算得矩阵P, 如下所示:

$P = \left( {\begin{array}{*{20}{c}} { 0}&{1}&{1}&{0}&{0}&{0}&{1} \\ { 1}&{0}&{1}&{1}&{1}&{0}&{1} \\ { 1}&{1}&{0}&{0}&{1}&{0}&{0} \\ { 0}&{1}&{0}&{0}&{1}&{1}&{0} \\ { 0}&{1}&{1}&{1}&{0}&{1}&{1} \\ { 0}&{0}&{0}&{1}&{1}&{0}&{1} \\ { 1}&{1}&{0}&{0}&{1}&{1}&{0} \end{array}} \right)$

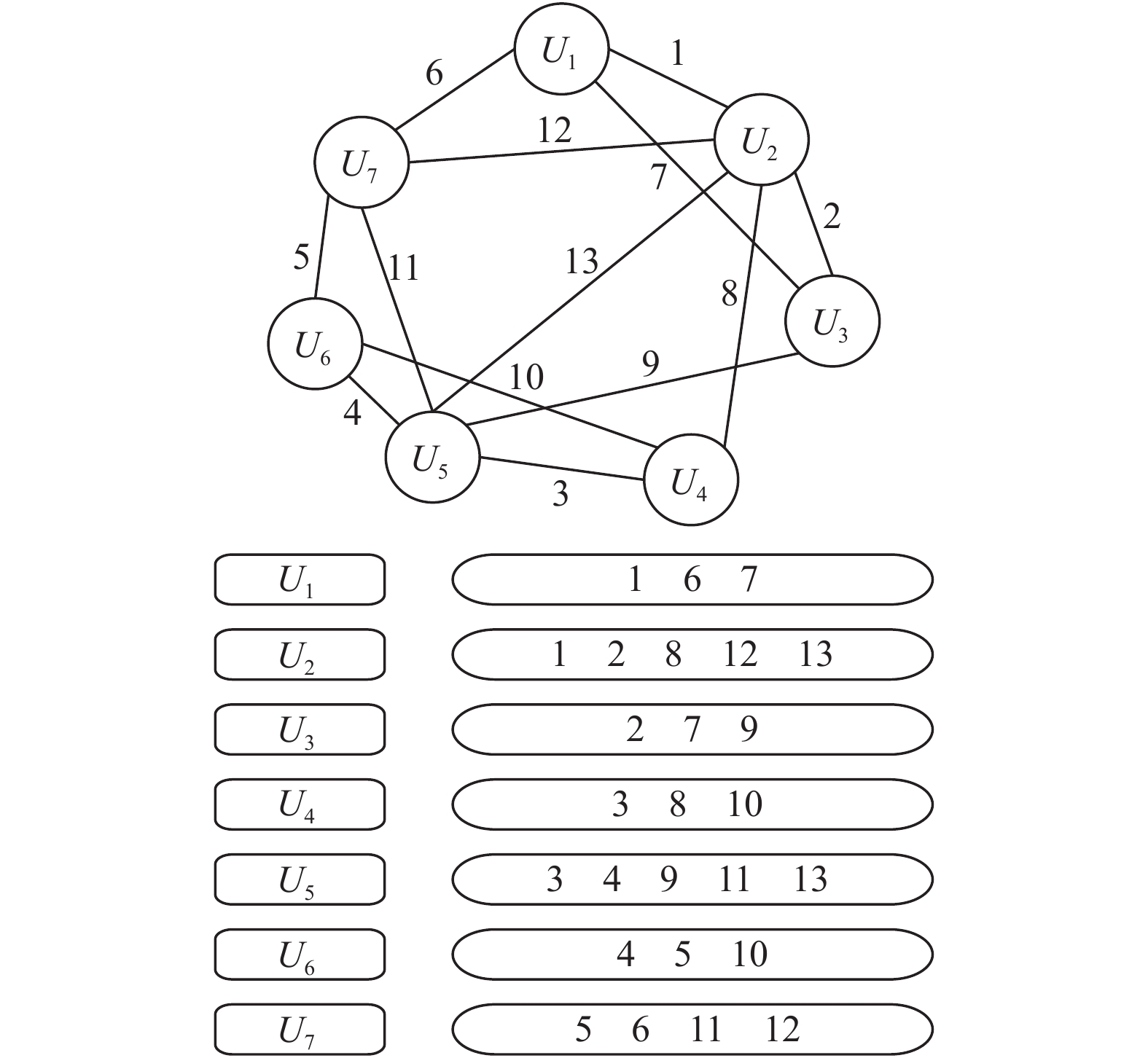
根据矩阵P能得到 (3, 4, 5)-部分正则图, 即部分正则图的度有5, 4, 3这三种情况, 也就对应节点存储容量有5, 4, 3三种情况, 如图1所示.

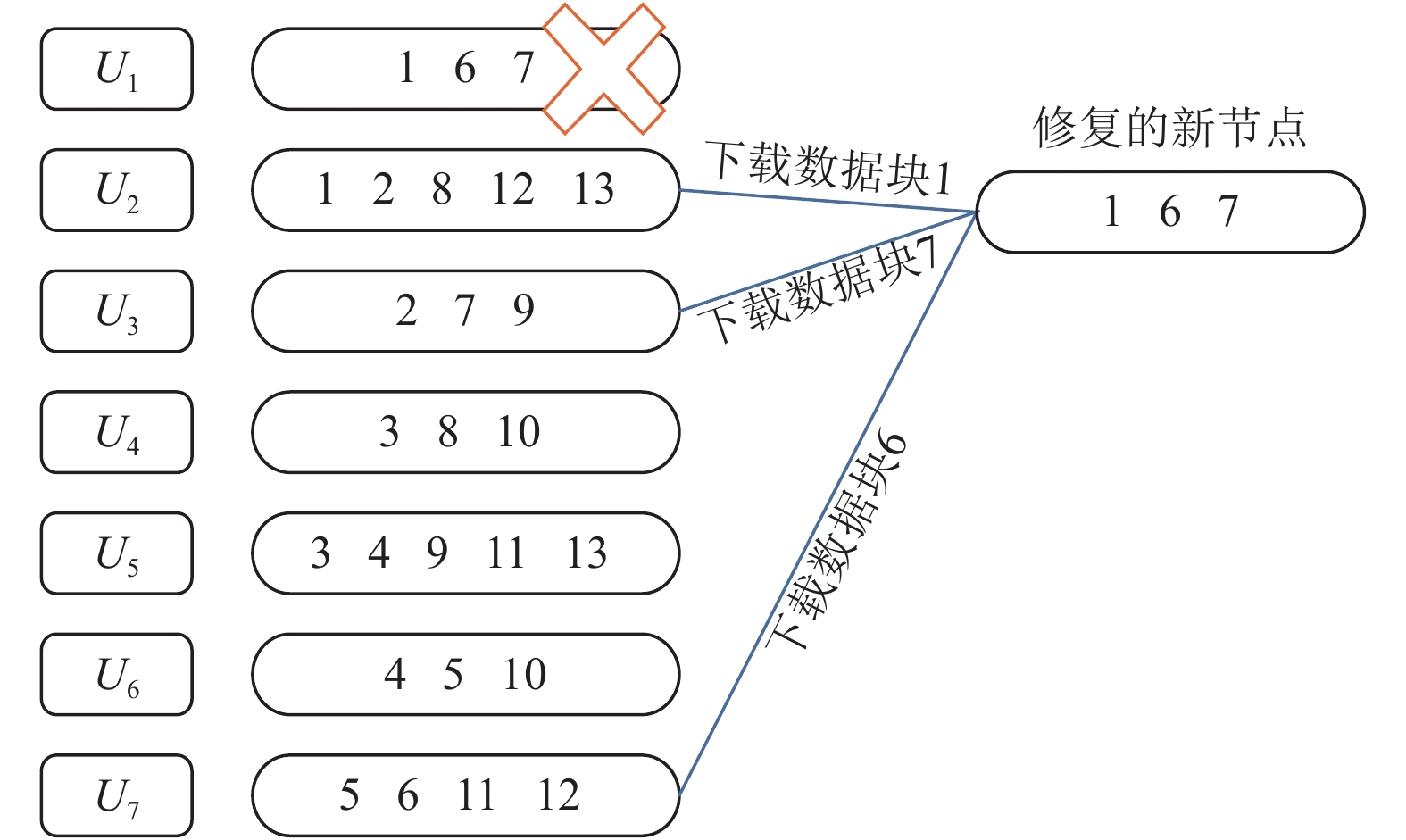
若节点U₁发生故障, 需连接U₂, U₃, U₇这3个节点进行修复, 即从U₂, U₃, U₇这3个节点下载1, 6, 7数据块进行修复, 修复过程如图2所示. 同理, 其他节点发生故障也可用相同的方法进行修复.

3 基于可调节环的FRC构造

本节运用可调节环结构构造FRC, 根据一定的存放规则去调节重复度的大小和节点存储容量, 规则是将数据元素放入相邻的节点所在环的边之间, 规定当每一个数据块依次放在两个相邻的节点之间时, 此时FRC的重复度为 $\rho = 2$ ; 当每一个数据块都放在3个相邻的节点之间, 此时FRC的重复度为 $\rho = 3$ , 同理可用相同的存放规则去调节重复度. 由同构FRC参数满足的条件 $n\alpha = \rho \theta $ 可知, 当给定的参数满足该条件时, 可得到同构的FRC, 若该等式不成立, 则可用可调节环构造节点存储容量异构的FRC, 根据已有的对FRC的研究中发现, 大部分只考虑重复度为2, 3的情况, 具体构造算法如下.

3.1 用可调节环去构造重复度 $\rho = 2$ 的FRC

假设系统中节点用 ${U_1},{U_2},\cdots,{U_n}$ 表示, 节点中的数据块用 $\theta $ 表示, 且 $\left[ \theta \right] = \{ 1,2,\cdots,\theta \}$ , 将数据块按一定规则放入环中, 即从节点 ${U_1}$ 开始, 将数据块1放在 ${U_1}$ 和 ${U_2}$ 所在的边上, 将数据块2放在 ${U_2}$ 和 ${U_3}$ 所在的边上, 数据块3放到 ${U_3}$ 和 ${U_4}$ 所在边上, 以此类推, 直到将 $\theta $ 个数据块放完为止.

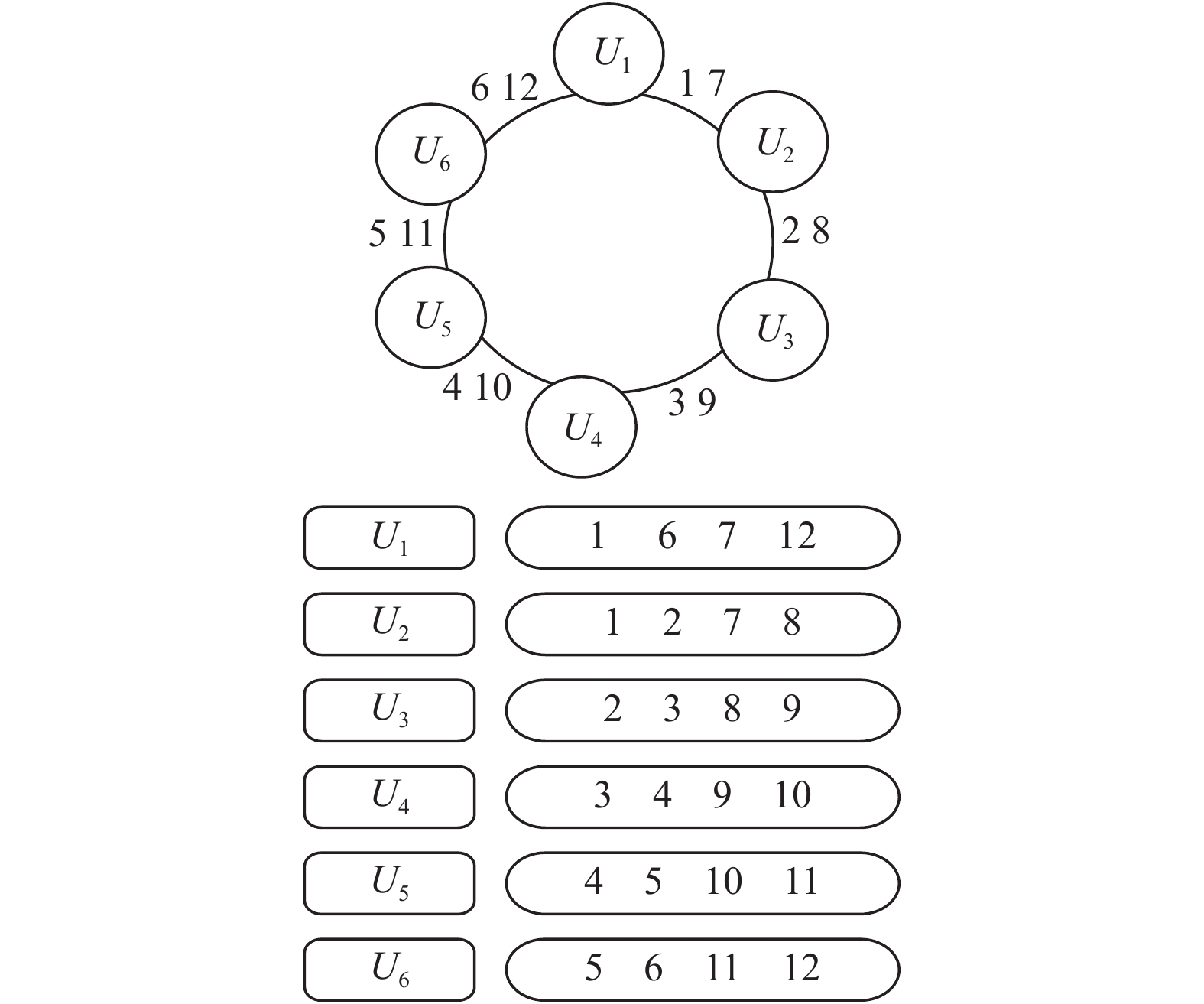
根据上述算法可以得到重复度 $\rho = 2$ 的FRC. 因为每一个数据块存在于相邻的2个节点所在环的边上, 每个数据块都会被两个节点所共有, 即得到的是重复度 $\rho = 2$ 的FRC. 若所给参数满足 $n\alpha = \rho \theta $ , 用可调节环可以构造节点存储容量同构的FRC, 否则用可调节环可以构造节点存储容量异构的FRC. 具体实例如下, 其中, 例2给定的是用可调节环构造的重复度 $\rho = 2$ 的同构FRC, 例3给定的是用可调节环构造的重复度 $\rho = 2$ 的异构FRC.

例2. 给定 $n = 6,\theta = 12$ , 用可调节环去构造FRC, 环结构和节点存储结构, 如图3所示.

由节点存储结构图可知该FRC满足 $n\alpha = \rho \theta $ , 是同构的FRC, 重复度 $\rho = 2$ , 节点储存容量为 $\alpha = 4$ , 若节点U₁故障, 需要从U₂下载数块1, 7, 从U₆下载数据块6和12修复U₁, 其他节点故障也可用相同的修复方式进行修复, 无需编码操作.

例3. 给定 $n = 8,\theta = 21$ , 用可调节环去构造FRC, 环结构和节点存储结构图, 如图4.

由节点存储结构图可知, 该FRC不满足 $n\alpha = \rho \theta $ , 是异构的FRC, 且重复度 $\rho = 2$ , 节点存储容量有4, 5, 6三种情况, 可修复单节点故障, 修复方式是直接从存活节点下载相应数据块进行修复.

3.2 用可调节环去构造重复度 $\rho = 3$ 的FRC

若分布式存储系统的节点用 ${U_1},{U_2},\cdots,{U_n}$ 表示, $\theta $ 表示存储在节点中的数据块, 且 $\left[ \theta \right] = \{ 1,2,\cdots,\theta \}$ , 将 $\theta $ 个数据块按一定的规则放入环中, 即从 ${U_1}$ 节点开始, 将数据块1分别放到 ${U_1}$ ${U_2}$ 和 ${U_2}$ ${U_3}$ 所在的边上, 将数据块2分别放到 ${U_2}$ ${U_3}$ 和 ${U_3}$ ${U_4}$ 所在边上, 数据块3放到 ${U_3}$ ${U_4}$ 和 ${U_4}{U_5}$ 所在边上, 以此类推, 直到将 $\theta $ 个数据块放完为止.

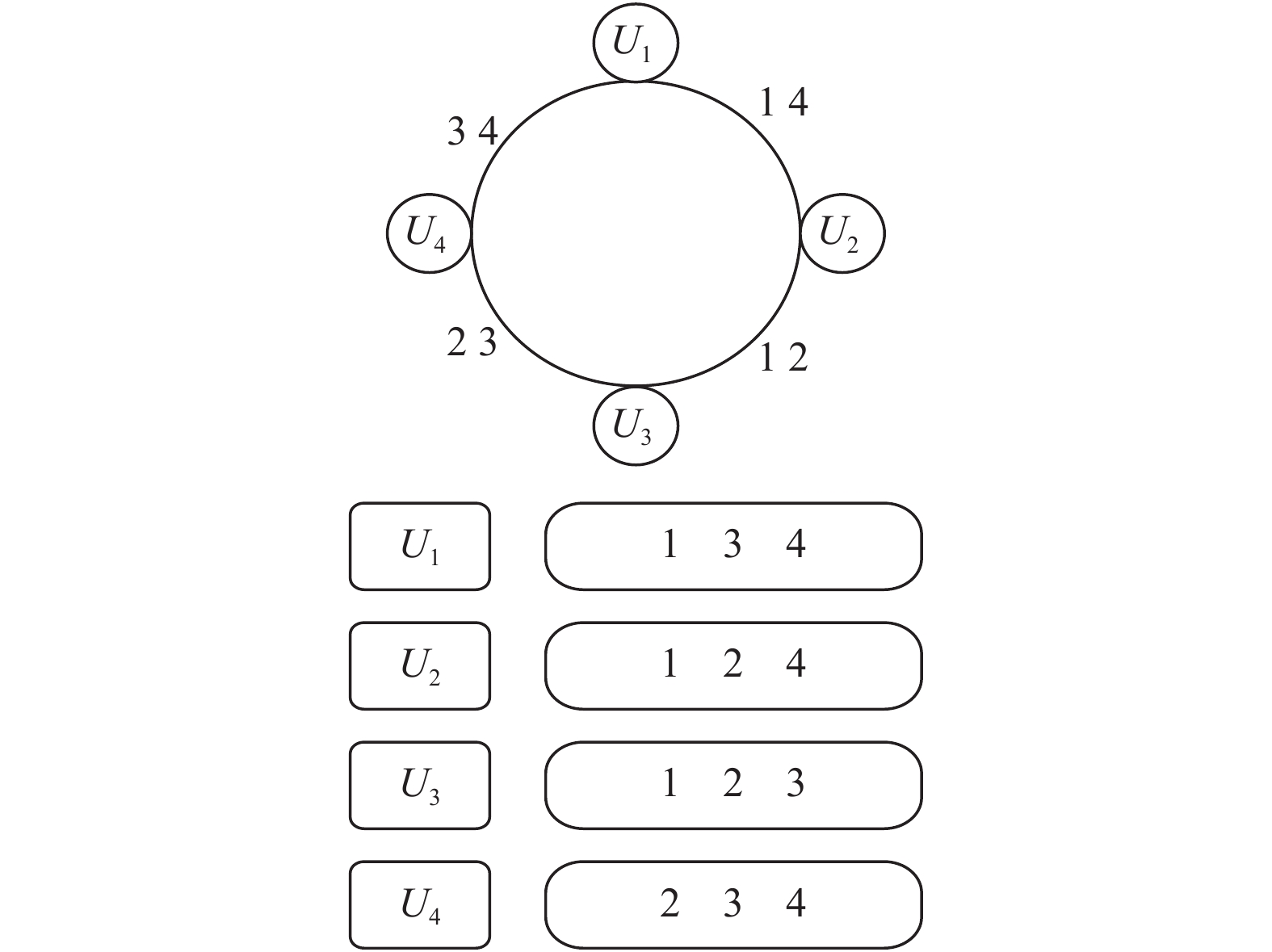
根据上述算法可得到重复度 $\rho = 3$ 的FRC. 因为每一个数据块存在于相邻的3个节点所在的环之间, 即每个数据块都会被3个节点共有, 则得到的是重复度 $\rho = 3$ 的FRC. 若所给参数满足 $n\alpha = \rho \theta $ , 用可调节环可以构造节点存储容量同构的FRC, 否则可以构造节点存储容量异构的FRC. 具体实例如下, 其中, 例4给定的是用可调节环构造的重复度 $\rho = 3$ 的同构FRC, 如图5所示, 例5给定的是用可调节环构造的重复度 $\rho = 3$ 的异构FRC, 如图6所示.

例4. 给定 $\theta = n = 4$ , 则用可调节环去构造FRC, 结构如下.

由上面的可调节环结构图和节点存储图可知, 构造得到的码是重复度 $\rho = 3$ , 节点存储容量为3的同构FRC. 该FRC的故障节点修复方式为, 当U₁发生故障, 可以直接重U₃中下载1, 3两个数据块, 再从U₂或U₄中下载4这个数据块; 当U₁和U₂同时发生故障时, 可以直接从U₃和U₄节点中下载数据块进行修复, 修复方式简单, 无需任何编码.

例5. 给定 $\theta = 16,n = 8$ , 用可调节环去构造FRC, 结构如下.

由上面的可调节环结构图和节点存储图可知, 构造得到的FRC是重复度 $\rho = 3$ , 节点存储容量异构的FRC, 节点容量出现7,6,5三种情况. 该FRC的故障节点修复方式为, 直接从存活节点下载数据块, 可最多修复两个故障节点.

4 性能分析

对本文提出的两种新的构造进行性能分析, 主要与现有的FRC对比分析, 发现本文构造的FRC在节点存储容量上具有异构的特点, 修复局部性好, 同时在构造算法运算复杂度低, 可以大范围的选择参数, 构造结构简单直观.

4.1 节点存储容量对比分析

对矩阵变换构造的异构FRC和已有的用正则图和部分正则图构造的FRC进行对比分析, 主要分析节点存储容量, 如表1.

表1只列举了部分情况, 可以发现本文提出的基于矩阵构造的异构FRC相比于正则图构造的FRC在节点存储容量上是异构的, 并且本文提出的构造方法在节点修复选择度上更优.

对基于可调节环构造的FRC进行对比分析, 相比于文献[10]提出的运用正则图构造的FRC本构造在重复度上的选择性更灵活, 正则图只能构造 $\rho = 2$ 的同构FRC, 用可环结构可以得到重复度多样的同构或异构的FRC, 构造算法更简单直观.

4.2 参数选择对比分析

根据已有研究表明, 大多数构造FRC的方法都对参数有明显的限制, 对比分析得本文提出的基于可调节环构造的FRC, 在参数选择上更具有灵活性, 对比分析结果, 如表2. 分析结果. 表2中各参数含义解释如下: $\alpha $ 是FRC的节点存储容量, $d$ 表示修复单个节点时需要连接的节点数, 一般意义上 $\alpha = d$ , $\rho $ 表示FRC的数据重复度, $\theta $ 表示系统中数据块, $n$ 表示系统中的节点数, $q$ 是素数, $h$ 是Hadamard矩阵的阶数.

4.3 修复局部性对比分析

修复局部性是指在修复故障节点时需要连接的存活节点数. 当单节点出现故障时, 运用正则图构造的FRC需要连接的节点数为d, 即修复局部性为d, 运用基于矩阵变换构造的异构FRC需要连接的节点数有 $d,d - 1,d - 2$ 三种情况, 即修复局部性为 $d,d - 1,d - 2$ 三种情况, 修复局部性更好. 另外, 当出现单节点故障时, (n, k)RS码需要连接k个节点先恢复原始文件来修复出现故障的节点, 修复局部性为k; 基于矩阵变换构造的异构FRC需要连接的节点数有 $d,d - 1,d - 2$ 三种情况, 修复局部性为 $d,d - 1,d - 2$ 三种情况, 又由于研究的FRC都是 $d < k$ , 所以可知和(n, k)RS对比, 基于矩阵变换构造的异构FRC具有更好的修复局部性.

图7给定的实例是基于矩阵变换构造的异构FRC和(n, k)RS码的在修复局部性方面的对比情况, 当修复节点存储容量为 $d(d < k)$ 的节点时, 可知基于矩阵变换构造的异构FRC的修复局部性恒为 $d(d < k)$ , 但RS码的修复局部性与k (正整数)是一次线性关系.

4.4 构造算法运算复杂度

衡量一个算法的优劣, 通常需要考虑算法构造时涉及的运算复杂度, 即将算法写成程序在实际的计算机系统中运行时, 涉及的计算量. 本文基于矩阵变换的异构FRC, 由构造算法可知, 构造一个异构的FRC需要进行 $d - 1$ 次加法运算和 ${n^2}$ 次模2加运算; 运用可调节环构造的FRC, 构造时不需要任何计算量, 只需在环上直接进行调节即可, 相比于基于矩阵变换的异构FRC, 用可调节环得到的FRC, 在构造算法运算复杂度表现的更优.

将基于矩阵变换的异构FRC和运用偏序集构造的FRC^[10]在构造算法运算复杂度进行对比分析, 在文献[10]中, 构造算法时运用到了加法, 乘法运算和基于集合上的运算, 明显可知本文算法运算复杂度更低.

5 结论

考虑实际的分布式存储系统大多需要满足异构的特性. 为此, 本文提出了两种构造方法, 一种是基于矩阵变换构造的异构FRC, 该构造主要用于构造重复度为2, 节点存储容量异构的FRC, 相比用正则图构造的同构FRC, 该构造更符合现实的存储系统; 另外, 本文还提出了运用可调节环构造的FRC, 构造得到了重复度为2或3的FRC, 该方法即可得到节点存储容量同构的FRC也可得到节点存储容量异构的FRC. 与现有的FRC对比分析, 发现本文构造的FRC在节点存储容量上具有异构的特点, 修复局部性好, 同时在构造算法运算复杂度低, 可以大范围的选择参数, 构造结构简单直观. 将来如何去构造更多样的异构FRC是研究的热点.