2. 武夷学院 认知计算与智能信息处理福建省高校重点实验室, 武夷山 354300;
3. 智慧农林福建省高校重点实验室, 福州 350002
2. Key Laboratory of Cognitive Computing and Intelligent Information Processing of Fujian Education Institutions, Wuyi University, Wuyishan 354300, China;
3. Key Laboratory of Smart Agriculture and Forestry of Fujian Education Institutions (Fujian Agriculture and Forestry University), Fuzhou 350002, China
大数据时代, 各个领域时刻都在产生大量的数据, 这些数据通常都是无标签的, 要确定每一个样本的标签通常是困难的. 机器学习算法中的无监督学习可以对无标签的数据进行学习, 以期能够揭示数据之间的联系或存在的内在规律. 聚类算法是无监督学习的代表, 可通过数据的相似属性将数据进行分组, 帮助人们增进对数据的理解, 如利用聚类技术发现具有类似功能的基因组, 检测疾病的时空分布模式等.
传统的聚类算法可大致划分为基于划分的方法, 基于层次的方法, 基于密度的方法, 基于谱图划分的方法和其他方法[1]. K-means是分割聚类的最早也是最出名的研究, 其对初始的质心选择有较强的依赖性, 且倾向于寻找圆形集簇. K-means只考虑了连通性, Kuwil等[2]提出一种重心聚类算法(Gravity Center Clustering, GCC), 同时兼顾连通性和内聚性, 且无需提供聚类的簇数. 基于密度的方法中, DBSCAN (Density-Based Spatial Clustering of Application with Noise)[3]可以对任意形状的数据聚类, 但确定其半径和包含的样本数量是一个难点, 且在簇间混合度较大时对样本标签误判的概率较高. 郭艳婕等[4]提出一种改进的GS-DBSCAN算法, 通过计算数据的分布特性, 可自适应确定半径和半径内包含的样本数。层次聚类算法包括分裂法和凝聚法, 其中, CURE (Clustering Using REpresentative)算法[5]能够处理形状和尺寸差别较大的簇, 对噪音点不敏感, 但对特殊形状的类簇识别能力较差. 基于图分割方法的谱聚类(Spectral Clustering)算法[6]也可以对任意形状的样本进行聚类, 且通常能够收敛于全局最优解, 但其计算的时间复杂度较高, 需要预先知道簇的数量, 构建合适的相似度矩阵是一个难点. 胡卓娅等[7]通过构造本征间隙序列, 可确定聚类的簇数. 最新的研究中, Xie等[8]提出一种互为最近邻的层次聚类算法(Reciprocal-nearest-neighbors Supported Clustering, RSC), 其假设互为最近邻居的两个样本一定会划分在同一个簇中.
对于高维数据, 要通过低维空间上的可视化观察其聚类特性是困难的, 这对传统聚类方法提出了挑战. 近年来, 基于复杂网络的机器学习方法得到了研究者的关注[9]. 将向量化的数据转换为以网络表示的数据, 其过程是无损的. 以网络表示的数据相比以向量表示的数据拥有更多的信息, 如样本之间的关系结构或者拓扑信息. 通过观测网络的拓扑结构, 更易于发现样本的聚类特性.
以Iris数据集为例, 从每个类别中抽取其中的前10个样本, 通过网络构建, 得到的结果如图1所示. 其中, 类别标签为Iris-virginica的节点中, 样本21和26的特征与类别Iris-versicolor非常接近, 经网络构建后, 其与类别Iris-versicolor中样本的联系较为紧密. 其余节点都能与同类别的节点保持稠密的连边关系.

|
图 1 Iris数据集部分样本的拓扑图 |
通过图1中的拓扑结构, 可以看到样本较为清晰的划分为3个簇, 同一簇中节点间的连边密度较大, 而簇之间的连边较为稀疏.
对向量表示的数据进行网络化后, 一种有效的聚类方法是进行社区发现[10]. 通常意义上, 社区内部的节点之间连边稠密, 而社区之间的连边稀疏.
Raghavan等[11]于2007年将一种半监督学习算法标签传播算法(Label Propagation Algorithm, LPA)[12]用于社区发现, 取得了良好的效果. LPA算法具有接近线性的时间复杂度, 这对规模越来越大的社交网络研究具有重要的意义. 然而, LPA算法为每个节点初始化一个标签, 容易造成标签传播的随机性, 并增加了传播过程的迭代次数. 将数据集进行网络化, 节点间的连边较为稀疏, 用LPA发现的社区数量一般远大于真实的类簇数量, 聚类准确度较差.
鉴于LPA具有接近的线性时间复杂度, 将LPA算法应用于数据聚类是一种有意义的尝试. 通过将向量表示的数据集构建为网络(数据集中的一个样本对应网络中的一个节点), 再用改进的LPA算法进行社区发现, 将网络中的节点划分到不同社区, 即实现了数据集中样本的聚类. 本文提出一种低随机性的改进LPA算法(Low Randomness Label Propagation Algorithm, LRLPA), 用于对网络化后的数据进行聚类. LRLPA算法主要针对LPA的两个不足进行改进. (1)对于LPA随机性较大的问题, 采用标签预处理和融入节点影响力的标签传播过程, 可有效降低其随机性. (2) LPA算法在稀疏网络上可能会产生较多的社区, 本文提出一种社区内聚度的社区质量衡量指标, 对内聚度低的社区进行优化合并, 可使得划分的社区质量更高, 且社区数量更接近真实的情况. 同时, LRLPA算法还保留了LPA的高效性.
1 相关工作 1.1 社区发现算法社区发现的相关算法中, 早期, 研究者主要基于图论及矩阵论, 提出用图分割和谱分析方法进行社区划分, 如KL算法[13]和谱划分算法[14,15]. 基于机器学习中聚类算法思想的延伸, Lin等[16]提出一种整数规划方法用于检测网络中的分层社区结构, SCAN算法[17]是基于密度聚类的经典社区发现算法. 基于模块度[18]优化的社区发现算法中, BGLL[19]在稀疏网络上有接近线性的时间复杂度, 克服了此类算法时间复杂度较大的缺点. 基于信息论的方法中, Infomap算法[20]利用网络上信息传播的规律来识别社区, 与Infomap算法类似, CDID算法[21]通过模拟网络中的信息交换来发现社区.
1.2 LPA算法LPA算法[11]的基本思想: 统计节点的邻居节点的社区归属情况, 某个标签对应的节点数量最多, 则选择该标签作为当前节点的标签. 其算法步骤如下.
步骤1. 为各节点选择一个唯一的标签, 通常将各节点标签初始化为节点的编号.
步骤2. 将所有节点随机洗牌后, 逐一更新节点标签. 根据当前节点的邻居节点标签情况, 选择对应节点数量最多的标签作为目标标签, 用以更新当前节点的标签. 如果满足条件的标签有多个, 则随机选择一个标签.
步骤3. 重复步骤2, 直到每一个节点的标签都不再发生变化为止.
步骤4. 将具有相同标签的节点划分为同一个社区, 算法终止.
1.3 LeaderRank算法LeaderRank[22,23]是基于PageRank[24]提出的用于网络中节点排序的算法. 与PageRank相比, 其增加了背景节点(ground node) g. 在有向网络中, 将g与所有其他节点双向连接, 而在无向网络中就是将g与所有节点建立连边. 计算每个节点的LR值, 该值越大, 表示该节点越重要. 社交网络中,
算法初始设定LRg(0)=0, LRi(0)=1, 即节点背景节点g的初始LR值为0, 网络中的其他节点初始的重要性相同, 都为1单位LR值. 在t时刻, 节点vi的LR值根据式(1)计算:
| $ L{R_i}(t) = \sum\limits_{{v_j} \in {\Gamma _i}}^{} {\frac{{{\delta _{ji}}}}{{k_j^{\rm out}}}} L{R_j}(t - 1) $ | (1) |
其中, Γi表示节点vi的邻居节点集合, kjout表示节点vj的出度, LRj(t–1)表示vj在t–1时刻的LR值. 在有向图中, vj是指向vi的节点, 在无向图中, vj是vi的邻居节点, 所以δij=1.
重复式(1)的计算直至LR值不再发生变化或变化程度小于阈值, 再根据式(2)修正所有节点的LR值.
| $ L{R_i} = L{R_i}({t_c}) + \frac{{L{R_g}({t_c})}}{N} $ | (2) |
其中, tc是式(1)收敛的迭代次数, LRg(tc)表示节点g迭代至收敛状态时的LR值.
2 算法定义与实现 2.1 网络构建一个包含n个样本的数据集表示为X={x1, x2, ···, xn}, xi表示第i个样本, 其具有r个属性, 即xi=(xi1, xi2, ···, xir). 将X中的样本构建为无权无向的全连接网络, 其对应的网络用G=(V, E)表示, V={v1, v2, ···, vn}是网络中节点的集合, E={e1, e2, ···, em}表示网络中边的集合, em={(vi, vj)|vi≠vj˄vi, vj
网络构建的目标是将空间中具有较近距离的样本之间建立连边关系, 且构建出的网络是一个连通图, 节点之间的连边尽量稀疏. 本文采用kNN和
kNN方法对样本xi寻找欧氏空间中距离最近的k个样本NNi={xj|与xi最近的k个节点}, 并在对应的网络中构建节点vi与NNi中样本对应节点的连边. kNN方法保证空间中处于边缘的点(噪音点)也能够与网络中其它节点建立连边关系, 使得数据集X中的所有样本都能出现在网络中.
2.2 标签预处理LPA算法步骤1中, 初始标签分布散乱, 标签传播的随机性较大, 容易导致标签误传播, 并增加算法的迭代次数. 一种可行的方法是对标签进行预处理, 使得相似度较高的节点具有相同的标签, 提升后续标签传播的稳定性, 缩减迭代次数.
用节点的共同邻居数衡量节点的相似度是一种常用的方法, 其定义如式(3):
| $ C{N_{i,j}} = \left| {{\Gamma _i} \cap {\Gamma _j}} \right| $ | (3) |
其中, vj∈Γi, 即只计算当前节点vi和邻居节点的相似度.
定义1. 标签初始化规则. 对于
| $ k = \mathop {\arg \max }\limits_{j \in {\Gamma _i}} C{N_{i,j}} $ | (4) |
| $ l{b_i} = \left\{ {\begin{array}{*{20}{l}} {l{b_k},}&{|k| = 1} \\ {l{b_{rand(k)}},}&{|k| > 1} \end{array}} \right. $ | (5) |
其中, rand(k)表示从集合k中随机选择一个.
2.3 融合节点影响力的标签传播标签传播阶段, LPA算法选择标签的方法是统计邻居节点的标签, 一个标签对应一组节点, 选择对应节点数最多的标签作为当前节点的标签. 有多个标签满足条件的, 就随机选择一个标签. 在节点连边较为稀疏的情况下, 尤其是当节点处于两个社区的连接路径上时, 以上方法容易造成标签误传播. 引入节点影响力, 在需要随机选择的情况下, 依据标签对应的节点LR值之和进行辅助选择, 进一步消除标签传播的随机性.
定义2. 融合节点影响力的标签传播规则. 节点vi的邻居节点中可能存在多个标签, 统计每个标签对应的节点数量, 某个标签对应的节点数量最多, 则选择该标签作为vi的标签. 式(6)统计节点vi邻居节点的标签归属情况, 并选出最大者:
| $ maxk = \mathop {\arg \max }\limits_k \sum\limits_{j \in \Gamma _i^k} {{\delta _{ij}}} $ | (6) |
当|maxk|=1时, lbi=lbmaxk. 当|maxk|>1时, 进一步计算每个标签对应节点的影响力(LR)之和, 选择节点LR值之和最大的标签作为目标标签. 式(7)计算标签对应的节点影响力之和, 并选择LR值之和最大者l作为节点vi的标签:
| $ l = \mathop {\arg \max }\limits_{k \in maxk} \sum\limits_{j \in \Gamma _i^k} {L{R_j}} $ | (7) |
其中, Γik表示节点vi的邻居节点中标签为k的节点集合. 因为此处讨论的节点vj是vi的邻居节点, 所以δij=1.
2.4 社区优化合并将向量表示的数据集进行网络化, 一般情况下要求构建的网络在确保全连通的前提下尽量稀疏, 网络中节点度通常不满足幂律分布. 用社区发现算法进行节点聚类, 在未指定社区数量的情况下, 得到的社区数通常会大于真实的簇的数量, 所以需要进行优化合并.
定义3. 内度与外度. 假设C={c1, c2,···, cl}是G的一次社区划分结果, cl称为一个社区. 节点vi
定义4. 社区内聚度. 社区内聚度定义为社区c中的节点的内度之和与外度之和的比值, 比值越大, 表示内聚度越高, 社区质量越好. 当比值小于设定的阈值时, 该社区需要与相邻社区合并. 社区内聚度表示为cohc:
| $ co{h_c} = \frac{{\displaystyle\sum\limits_{i \in c} {d_i^{\rm in}(c)} }}{{\displaystyle\sum\limits_{i \in c} {d_i^{\rm out}(c)} }} $ | (8) |
定义5. 社区优化合并规则. 当cohc<
| $ t = \mathop {\arg \max }\limits_l \sum\limits_{i \in c} {{\rm{|}}d_i^{\rm out} \in {c_l}{\rm{|}}},c \ne {c_l} $ | (9) |
当|t|=1时, lbi∈c=t; 当|t|>1时,lbi∈c=rand(t).
2.5 算法伪代码根据以上定义, 本文算法分为4个步骤: 首先对数据集进行网络化; 之后, 利用节点相似度对节点标签进行预处理, 以提高后续标签传播的稳定性; 在标签传播阶段, 用节点影响力辅助标签选择, 进一步降低标签传播的随机性; 最后, 通过对社区的内聚度进行判断, 对内聚度较小的社区进行合并优化, 以提高社区的质量.
算法1. CreatGraph
输入: X,y, maxk, eps
输出: G
1 X=MinMaxScaler(X)
2 dist=kNN(X, maxk)
3 Foreach xi∈X do
4 NBi={xj|dist(xi, xj)<eps}
5 if |NBi|≥k then
6 G.addEdge(xi, NBi)
7 else
8 NNi={xj|与xi最近的k个节点}
9 G.addEdge(xi, NNi)
10 end
11 end
12 return G
算法1用于将数据集转换为对应的网络, 其主要步骤如下:
1)首先对数据进行最大最小值归一化, 即将各列特征值缩放到[0,1]之间, 以消除列之间特征值量纲不同引起的问题, 归一化的公式为:
| $ {x_{norm}} = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} $ | (10) |
2)利用kNN算法求样本之间的距离, 并使用k-d树进行求解. 对于高维数据, 用k-d树可将时间复杂度降低为O(NlogN)(第2行);
3)求与样本xi的距离在半径eps范围内的样本点(第4行);
4)如果在半径距离内的样本数大于等于k, 在图G中添加节点vi与NBi中所有样本对应的节点的边; 否则计算NNi, 并建立vi与NNi中节点的连边. 其中addEdge函数用于在节点对之间建立边, 因为构建的是无向图, 两个节点之间最多只建立一条边(第5–10行);
5)最后返回构建完成的网络G(第12行).
算法2. InitLabel
输入: G=(V, E), γ
输出: LB
1 LB={lbi=i|vi∈V}
2 Foreach vi ∈V do
3
4 if |k|==1 then
5 lbi=lbk
6 else
7 lbi=lbrand(k)
8 end
9 update(LB, lbi)
10 end
11 return LB
算法2根据相邻节点间的共同邻居数对节点进行标签初始化, 主要步骤如下:
1)初始化节点标签为其对应的编号(第1行);
2)计算节点vi与邻居节点的共同邻居数, k中保留与vi具有最多共同邻居数的节点标签(第3行);
3)根据定义1对标签进行预处理(第4–8行);
4)用新的标签更新标签集合LB, 此处采用异步更新(第9行).
算法3. InfluLPA
输入: G, LB
输出: C
1 LR=LeaderRank(G)
2 finished=false
3 LBO=LB
4 While not finished do
5 LBN=Φ
6 Foreach vi ∈V do
7
8 if |maxk|=1 then
9 lbi=lbmaxk
10 else
11
12 lbi=lbl
13 end
14 LBN=LBN
15 end
16 if LBN==LBO then
17 finished=true
18 else
19 LBO = LBN
20 end
21 end
22 C=part(LBO)
23 return C
算法3的主要步骤如下:
1)用LeaderRank算法计算节点的LR值, 用于后续的标签选择(第1行);
2)根据定义2进行一趟标签传播(第6–15行);
3)一趟标签传播后, 如果所有标签未发生变化, 迭代结束; 否则进行下一趟的标签传播(第16–20行);
4) part函数根据节点的标签将节点划分为不同的社区(第22行).
算法4. CombComm
输入: C,
输出: C’
1 C’=C
2 Foreach c ∈ C do
3
4 if cohc<
5
6 if |t|==1 then
7 lbi∈c=t
8 else
9 lbi∈c=rand(t)
10 end
11 ct=ct
12 C'=updata(C', c, ct)
13 end
14 end
15 return C'
算法4根据社区内聚度进行社区优化合并, 其主要步骤如下:
1)复制原始社区C到C'(第1行);
2)根据定义4计算当前社区的内聚度(第3行);
3)当内聚度小于阈值
4)对C'中的社区进行更新, 删除社区c, 用更新后的社区ct更新C'(第11–12行).
2.6 时间复杂度分析算法1中进行数据归一化的时间复杂度为O(N); 利用基于k-d树的kNN算法求N个节点的最近邻节点和距离的时间复杂度为O(NlogN); 第3–11行构建图的时间复杂度为O(N). 算法1的总体时间复杂度为O(NlogN).
算法2中初始化节点标签的时间复杂度为O(N); 设节点的平均度为k, 计算无向图中相邻节点的共同邻居数的时间复杂度为O(k), 每个节点需要与k/2个邻居节点求交集, 则求N个节点与邻居节点相似度的时间复杂度为O(Nk2/2). 之后, 当前节点从邻居节点中选择一个标签的时间为O(k), 为N个节点选择标签的时间复杂度为O(kN). 算法2的总体时间复杂度为O(Nk2/2+Nk+k), 又因为k=2M/N, 则总时间复杂度可简单表达为O(kM).
算法3中, 计算节点的LR值的时间复杂度为O(M+N), 第2–21行的主体是LPA算法, 其时间复杂度为O(TM+N), T为迭代次数. 第11行需要计算节点的LR值之和, 最坏情况下, 一次计算的时间复杂度为O(k), 一般需要执行该计算的次数小于0.1×N, 本文研究中的k值一般小于10, 即最坏情况下该步骤的时间复杂度为O(N); 最后, 将节点划分到社区所需的计算量为O(N). 所以, 算法3总的时间复杂度为O(TM+N).
算法4中, 计算一个节点的内度和外度所需时间为O(k), 计算所有社区的内聚度需要计算所有节点的内度和外度, 其时间复杂度为O(kN); 对于不满足内聚度的社区, 需要查询节点外度的归属社区, 所需查询的节点数小于N, 则该步骤所需的计算机小于O(kN); 第12行更新社区的计算量为O(N). 算法4的总体时间复杂度为O(kN), 即O(M).
综上, 以上4个步骤的总体时间复杂度为O(NlogN+kM+TM+N+M), 实验结果表明, 迭代次数T一般小于10, 节点度k也一般小于10, 则时间复杂度可简化为O(M+NlogN).
3 实验及结果分析为验证算法的有效性, 本文选取Sklearn工具包中的K-means, DBSCAN和Spectral Clustering (SC) 3个算法作为对比算法, 各算法在不同数据集上的参数设定以取得最大NMI值为准则进行设置. 实验数据为15次运行结果的平均值。
实验环境: Intel(R) Core(TM) i7-8650U CPU, 16 GB内存, Windows 10操作系统, 算法采用Python 3.7实现.
3.1 实验数据集本文用Sklearn工具包中的make_blobs函数生成4个人工数据集, 用make_circles函数生成一个数据集, 并选择UCI上的Iris, Wine, Letter-recognition(LR), WDBC和Glass等5个数据集进行实验. 真实数据集的样本数量、特征数和簇数如表1所示, make_blobs的参数值设定如表2所示, make_circles的参数设定为n_samples=160, noise=0.1, factor=0.5. 为方便后续描述, 将make_circles生成的数据集命名为N5.
| 表 1 真实数据集 |
| 表 2 make_blobs参数值 |
3.2 评价指标
对于已知样本标签的数据集, 可采用标准化互信息(NMI)和调整兰德系数(ARI)两个指标对聚类算法准确性进行评价.
NMI定义为:
| $ NMI(A,B) = \dfrac{{ - 2\displaystyle\sum\limits_{i = 1}^{{C_A}} {\displaystyle\sum\limits_{j = 1}^{{C_B}} {{M_{ij}}\log \left(\frac{{{M_{ij}}N}}{{{M_{i \cdot }}{M_{ \cdot j}}}}\right)} } }}{{\displaystyle\sum\limits_{i = 1}^{{C_A}} {{M_{i \cdot }}\log \left(\frac{{{M_{i \cdot }}}}{N}\right) + \displaystyle\sum\limits_{j = 1}^{{C_B}} {{M_{ \cdot j}}\log \left(\frac{{{M_{ \cdot j}}}}{N}\right)} } }} $ | (11) |
其中, A是样本真实标签, B是算法聚类后的样本标签, N是样本数. CA是真实簇数量, CB是经算法聚类的簇数量. M是混淆矩阵, Mi·是矩阵M中第i行元素之和, 表示A中第i个簇的样本数. 相应的, M·j表示B中第j个簇的样本数, 即矩阵M中第j列元素之和. Mij表示A中第i个簇的样本属于B中第j个簇的样本数. NMI的值域为[0,1], 值越大则表示算法的聚类效果越好, 当NMI(A, B)=1时, 表示A和B的结构完全相同.
ARI定义为:
| $ \begin{split} & ARI = \\ & \dfrac{{{{\displaystyle\sum\limits_{ij} {\left( {\begin{array}{*{20}{c}} {{n_{ij}}} \\ 2 \end{array}} \right)} - \left[ {\displaystyle\sum\limits_i {\left( {\begin{array}{*{20}{c}} {{n_{i \cdot }}} \\ 2 \end{array}} \right)\displaystyle\sum\limits_j {\left( {\begin{array}{*{20}{c}} {{n_{ \cdot j}}} \\ 2 \end{array}} \right)} } } \right]} \Bigg/ {\left( {\begin{array}{*{20}{c}} n \\ 2 \end{array}} \right)}}}}{{\dfrac{1}{2}\left[ {\displaystyle\sum\limits_i {\left( {\begin{array}{*{20}{c}} {{n_{i \cdot }}} \\ 2 \end{array}} \right) + \displaystyle\sum\limits_j {\left( {\begin{array}{*{20}{c}} {{n_{ \cdot j}}} \\ 2 \end{array}} \right)} } } \right] - {{\left[ {\displaystyle\sum\limits_i {\left( {\begin{array}{*{20}{c}} {{n_{i \cdot }}} \\ 2 \end{array}} \right)\displaystyle\sum\limits_j {\left( {\begin{array}{*{20}{c}} {{n_{ \cdot j}}} \\ 2 \end{array}} \right)} } } \right]} \Bigg/ {\left( {\begin{array}{*{20}{c}} n \\ 2 \end{array}} \right)}}}} \end{split} $ | (12) |
其中, n是混淆矩阵, nij表示混淆矩阵中第i行第j列元素, ni·是混淆矩阵中第i行元素之和, n·j是混淆矩阵中第j列元素之和,
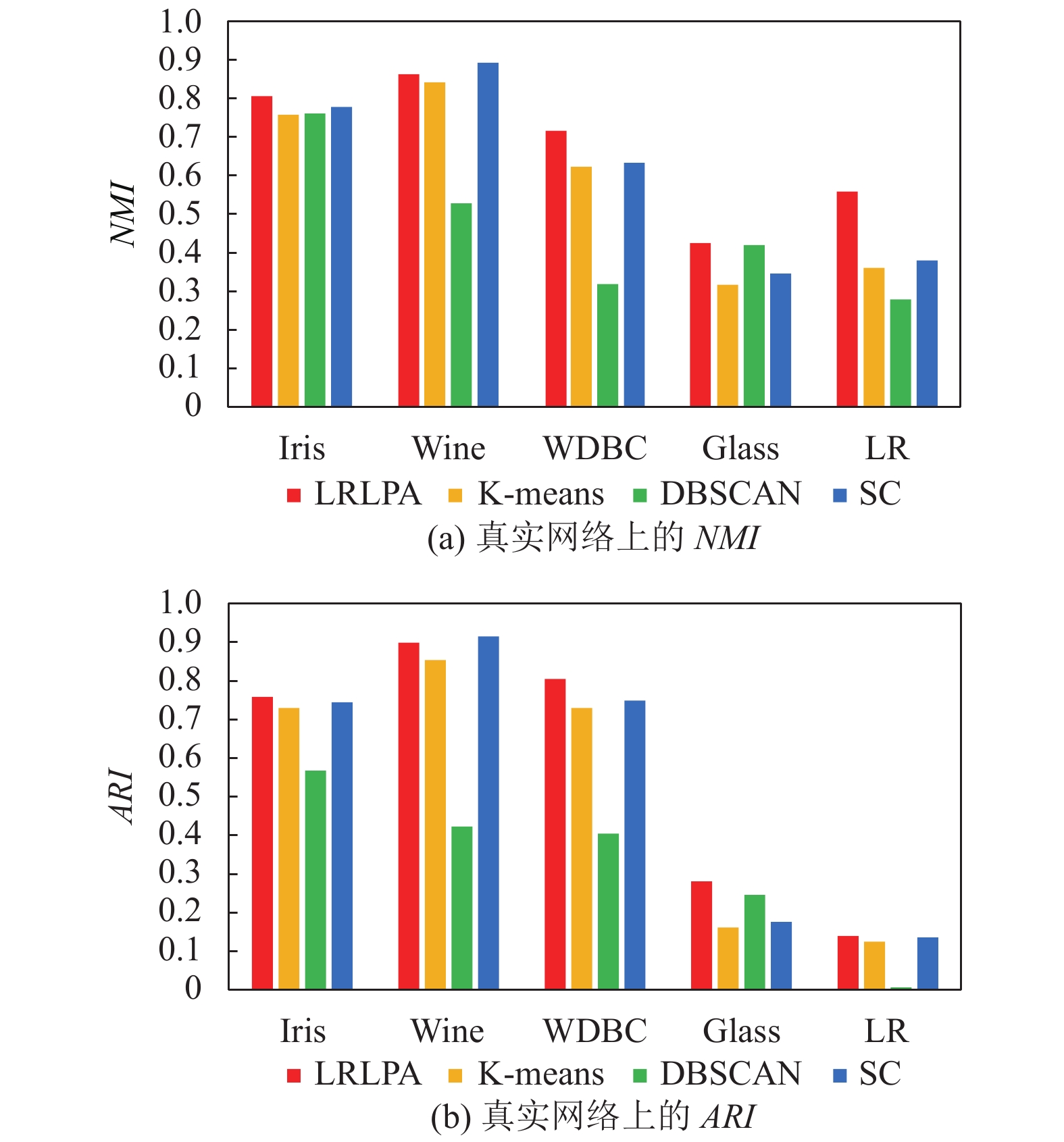
在Iris等5个真实网络上的实验结果如图2所示, 图2(a)是算法得到的NMI值, 图2(b)是算法得到的ARI值. 对于NMI指标, 本文算法在Iris, WDBC, Glass和LR等4个数据集上获得最优值. 在Wine数据集上, Spectral Clustering算法取得最优值, 本文算法得到的结果优于K-means和DBSCAN. 在ARI指标上得到的实验结果与在NMI上得到的结果类似.
|
图 2 不同算法在真实网络上的精度实验 |
在人工数据集上, 本文算法也取得了较好的结果. 图3(a)中, 在N1数据集上, 本文算法和Spectral Clustering都能够完全正确的对数据进行划分, 得到的NMI和ARI值都是1. 在N2数据集上, 本文算法得到的结果与K-means和Spectral较为接近. 在N3和N4数据集上, 本文算法得到的结果明显优于对比算法. 图3(b)中的ARI实验结果与NMI的结果类似.

|
图 3 不同算法在人工网络上的精度实验 |
在前4个数据集中, 都存在标准差为3的簇, 使得数据集中存在较多的噪音点, DBSCAN算法依赖于于样本密度, 对噪音点的识别能力较弱, 所以在4个数据集上的准确性都比较差. 本文算法在网络构建过程同时考虑了密度和k个最近邻样本, 保证了距离簇中心较远的样本也能与该簇中节点保持较多的连边, 有利于后续的社区发现. N5数据集是两个同心圆, 两个圆之间有部分节点重叠, Spectral Clustering算法无法区分簇之间的界限, 划分出的结果与真实情况差别较大, K-means算法对这种特殊类型的图形无法识别, 得到的NMI和ARI都为0, 而LRLPA和DBSCAN基于密度, 能够在密度较小的区间进行划分, 所以两者得到的结果比较接近.
3.4 算法稳定性实验LRLPA和LPA两种算法在人工数据集上的实验结果如图4所示. 无论是在NMI还是ARI指标上, 本文提出的LRLPA都比原始LPA具有更高的精确度, 且具有更小范围的误差. 对数据集X进行网络化后, 一般会比较稀疏, LPA识别出的社区数较多, 使得准确度指标不高. 而LRLPA最后一步根据内聚度进行优化合并, 使得社区数与真实簇数相同或接近, 提高了算法的精确度. 同时, 标签预处理与融入节点影响力的标签传播对降低算法随机性有较为明显的效果, 在4个数据集上的波动范围都小于2%.

|
图 4 LRLPA和LPA的精度即稳定性实验 |
4 结论与展望
本文提出了一种基于网络社区发现的低随机性标签传播聚类算法LRLPA. 在5个真实数据集和5个人工数据集上进行了实验, 与其他算法相比, LRLPA算法在大部分数据集上都具有最大的NMI和ARI值. 与LPA的对比中, 本文算法的准确率和稳定性都高于LPA.
下一步研究中, 一个改进的方向是通过动态网络构建, 将LRLPA算法应用于增量式聚类. 另一个值得注意的方向是改进标签传播方式, 将标签选择过程并行化, 提高算法效率, 以适应大规模数据集的应用.
| [1] |
雷小锋, 陈皎, 毛善君, 等. 基于随机kNN图的批量边删除聚类算法. 软件学报, 2018, 29(12): 3764−3785. DOI:10.13328/j.cnki.jos.005327 |
| [2] |
Kuwil FH, Atila Ü, Abu-Issa R, et al. A novel data clustering algorithm based on gravity center methodology. Expert Systems with Applications, 2020, 156: 113435. |
| [3] |
Ester M, Kriegel HP, Sander J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise. Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining. Portland, OR, USA. 1996. 226−231.
|
| [4] |
郭艳婕, 杨明, 侯宇超, 等. 基于相似性度量的改进DBSCAN算法. 数学的实践与认识, 2020, 50(6): 164-170. |
| [5] |
Guha S, Rastogi R, Shim K. CURE: An efficient clustering algorithm for large databases. Proceedings of 1998 ACM SIGMOD International Conference on Management of Data. Seattle, WA, USA. 1998. 73−84.
|
| [6] |
Ng AY, Jordan MI, Weiss Y. On spectral clustering: Analysis and an algorithm. Advances in Neural Information Processing Systems. Vancouver, BC, Canada. 2001. 849−856.
|
| [7] |
胡卓娅, 翁健. 基于人工蜂群算法的自适应谱聚类算法. 重庆理工大学学报(自然科学), 2020, 34(3): 137-144. |
| [8] |
Xie WB, Lee YL, Wang C, et al. Hierarchical clustering supported by reciprocal nearest neighbors. Information Sciences, 2020, 527: 279-292. |
| [9] |
Silva TC, Zhao L. High-level pattern-based classification via tourist walks in networks. Information Sciences, 2015, 294: 109-126. |
| [10] |
Girvan M, Newman MEJ. Community structure in social and biological networks. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12): 7821-7826. |
| [11] |
Raghavan UN, Albert R, Kumara S. Near linear time algorithm to detect community structures in large-scale networks. Physical Review E, 2007, 76(3): 036106. |
| [12] |
Zhu X, Ghahramani Z. Learning from labeled and unlabeled data with label propagation. Pittsburgh, PA, USA: Carnegie Mellon University, 2002.
|
| [13] |
Kernighan BW, Lin S. An efficient heuristic procedure for partitioning graphs. The Bell System Technical Journal, 1970, 49(2): 291-307. |
| [14] |
Fiedler M. Algebraic connectivity of graphs. Czechoslovak Mathematical Journal, 1973, 23(2): 298-305. |
| [15] |
Newman MEJ. Spectral methods for community detection and graph partitioning. Physical Review E, 2013, 88(4): 042822. |
| [16] |
Lin CC, Kang JR, Chen JY. An integer programming approach and visual analysis for detecting hierarchical community structures in social networks. Information Sciences, 2015, 299: 296-311. |
| [17] |
Xu XW, Yuruk N, Feng ZD, et al. SCAN: A structural clustering algorithm for networks. Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Jose, CA, USA. 2007. 824–833.
|
| [18] |
Newman MEJ, Girvan M. Finding and evaluating community structure in networks. Physical Review E, 2004, 69(2): 026113. |
| [19] |
Blondel VD, Guillaume JL, Lambiotte R, et al. Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment, 2008, 2008(10): P10008. |
| [20] |
Rosvall M, Bergstrom CT. Maps of random walks on complex networks reveal community structure. Proceedings of the National Academy of Sciences of the United States of America, 2008, 105(4): 1118-1123. |
| [21] |
Sun ZJ, Wang B, Sheng JF, et al. Community detection based on information dynamics. Neurocomputing, 2019, 359: 341-352. DOI:10.1016/j.neucom.2019.06.020 |
| [22] |
Lü LY, Zhang YC, Yeung CH, et al. Leaders in social networks, the delicious case. PLoS One, 2011, 6(6): e21202. |
| [23] |
Li Q, Zhou T, Lü LY, et al. Identifying influential spreaders by weighted LeaderRank. Physica A: Statistical Mechanics and Its Applications, 2014, 404: 47-55. |
| [24] |
Brin S, Page L. The anatomy of a large-scale hypertextual web search engine. Computer Networks and ISDN Systems, 1998, 30(1–7): 107-117. |
| [25] |
刘世超, 朱福喜, 甘琳. 基于标签传播概率的重叠社区发现算法. 计算机学报, 2016, 39(4): 716-729. |
 2020, Vol. 29
2020, Vol. 29



