不同类型的磨粒, 由于磨损类型和形成机理不同, 会表现出不同的形态特征, 这些形态特征是判断磨粒所属类型的重要依据. 正常磨粒、球状磨粒和切削磨粒等类型的磨粒一般在尺寸上和轮廓形态特征上具有鲜明的特点, 与其他类型的磨粒区别比较明显, 根据磨粒图像的形状特征对这些类型的磨粒进行分类时, 识别准确率一般都比较高; 而严重滑动磨粒、疲劳剥块和层状磨粒等类型磨粒的轮廓非常不规则, 并且表现出一定的相似性, 采用图像处理技术对这些类型的磨粒进行分类时, 对磨粒图像形状特征的要求就比较高. 因此研究磨粒图像形状特征提取方法, 对于提高磨粒类型识别的准确率具有重要的意义.

高阶统计量是描述随机过程高阶统计特性的一种数学工具, 包括高阶矩、高阶累计量以及它们的傅里叶变换——高阶矩谱和高阶累计谱, 高阶累计谱简称高阶谱. 最常用的高阶谱是三阶谱和四阶谱, 通常称为双谱和三谱. Chandran等^[1]在1993年根据高阶谱, 定义了一系列具有旋转和尺度不变性质的特征参数, 用于一维信号模式识别. 自1997年, Chandran^[2]首次将高阶谱分析推广到二维图像和物体识别领域, 近年来在这些领域得到了成功应用, 例如声纳图像中海矿识别^[3], 电子显微镜图像中病毒识别^[4]和热成像中乳腺癌检测^[5]. 文献[1-5]中都是采用Radon变换将图像映射到一组一维投影, 对一维信号进行双谱分析.

图像识别中的形状信息一般更多的包含在图像的相位而不是幅度之中. 普通的傅里叶变换, 其幅度特征丢失了图像的全部相位, 与之相比, 双谱保留了除线性相位之外的全部信号信息. 双谱分析通过对含高斯噪声序列的双谱估计, 重构频域的幅度与相位, 理论上可以完全去除独立的高斯噪声. 在此基础上本文提出了基于形状标记和双谱分析的形状特征提取方法, 采用形状标记得到图像的一维信号表示, 然后对形状标记进行双谱分析, 在双谱域提取双谱不变量特征作为图像的形状特征.

1 双谱的定义

高于二阶的累积量, 通常称为高阶统计量, 它们的多维傅里叶变换称为多谱. 假设累积量 ${c_{kx}}({\tau _1},{\tau _2}, \cdots ,{\tau _{k - 1}})$ 是绝对可求和的^[6], 即:

$\sum\limits_{{\tau _1}, \cdots ,{\tau _{k - 1}} = - \infty }^\infty {\left| {{c_{kx}}({\tau _1},{\tau _2}, \cdots ,{\tau _{k - 1}})} \right|} < \infty $

(1)

则 $k$ 阶谱定义为 $k$ 阶累积量的 $(k - 1)$ 维离散时间傅里叶变换, 即:

$\begin{split} &{S_{kx}}({\omega _1},{\omega _2}, \cdots ,{\omega _{k - 1}}) = \\ &\sum\limits_{{\tau _1} = - \infty }^\infty {\sum\limits_{{\tau _2} = - \infty }^\infty { \cdots \sum\limits_{{\tau _{k - 1}}}^\infty {{c_{kx}}({\tau _1},{\tau _2}, \cdots ,{\tau _{k - 1}})\exp ( - j{{\bf{\omega }}^{\rm T}}{\bf{\tau }})} } } \end{split} $

(2)

式中, ${\bf{\omega }} = {[{\omega _1},{\omega _2}, \cdots ,{\omega _{k - 1}}]^{\rm T}}$ , ${\bf{\tau }} = {[{\tau _1},{\tau _2}, \cdots ,{\tau _{k - 1}}]^{\rm T}}$ .

双谱即三阶谱, 定义为:

${B_x}({\omega _1},{\omega _2}) = \sum\limits_{{\tau _1} = - \infty }^\infty {\sum\limits_{{\tau _2} = - \infty }^\infty {{c_{3x}}({\tau _1},{\tau _2}){e^{ - j({\omega _1}{\tau _1} + {\omega _2}{\tau _2})}}} } $

(3)

对于一个离散时间能量有限的随机信号 $x(t)$ , 将双谱定义为:

${B_x}({\omega _1},{\omega _2}) = X({\omega _1})X({\omega _2}){X^*}({\omega _1},{\omega _2})$

(4)

式中, $X(\omega )$ 为信号 $x(t)$ 的傅里叶变换.

文献[5]指出提取双谱不变量时, 归一化的双谱要比原始的双谱效果好, 本文在提取双谱不变量特征时, 以归一化双谱为基础, 归一化的双谱如下式所示:

${B_N}({\omega _1},{\omega _2}) = \frac{{E\left[ {X({\omega _1})X({\omega _2}){X^*}({\omega _1} + {\omega _2})} \right]}}{{\sqrt {\left[ {P({\omega _1})P({\omega _2})P({\omega _1} + {\omega _2})} \right]} }}$

(5)

式中, $P(\omega )$ 为功率谱.

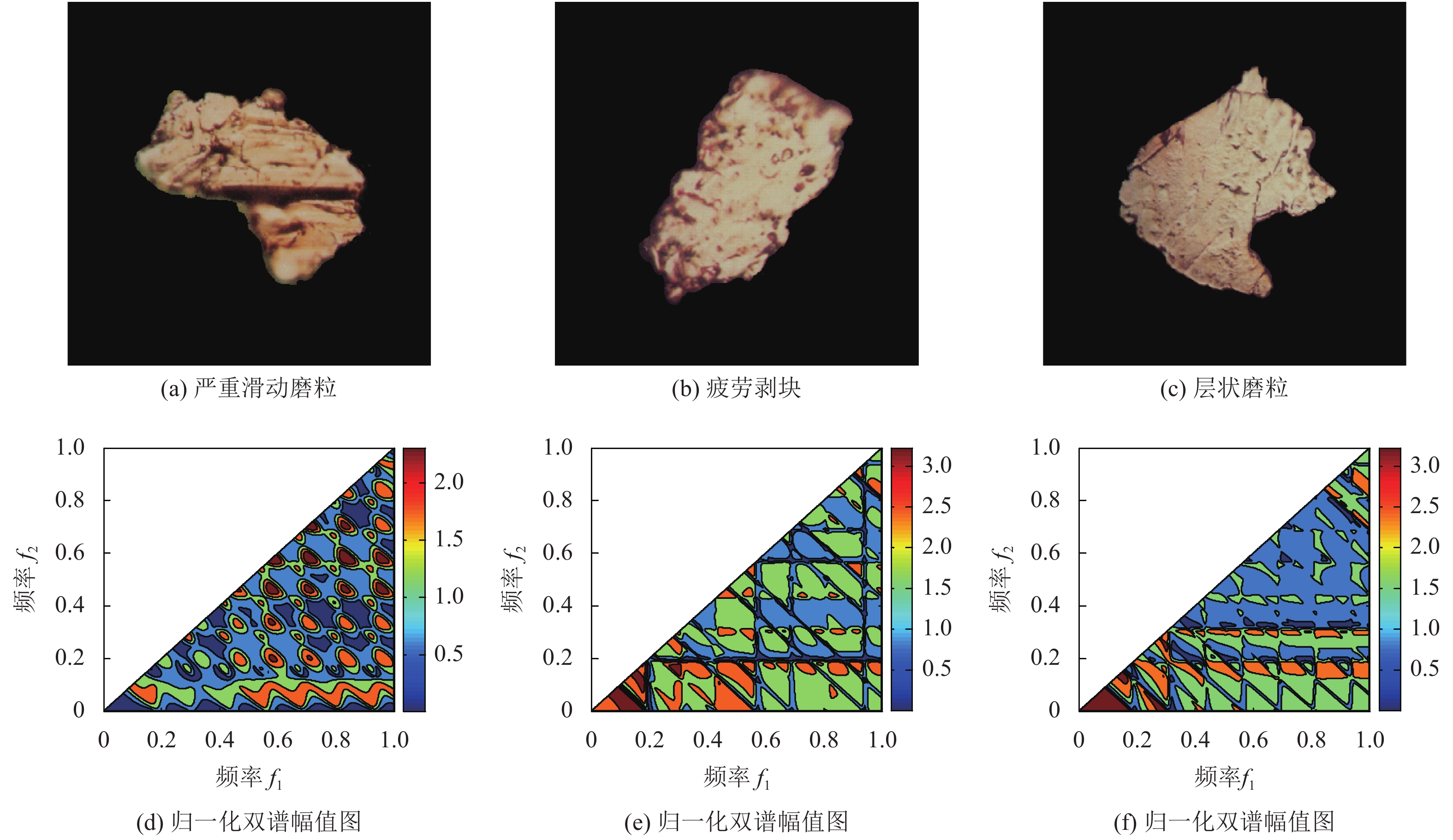
图1(a)、图1(b)和图1(c)分别为文献[7]中经过图像分割之后的3种典型的严重滑动磨粒、疲劳剥块和层状磨粒, 图1(d)、图1(e)和图1(f)分别为3种类型磨粒的归一化双谱的对数幅值图. 此处计算磨粒图像的双谱时, 采用Radon变换的方法将图像变为一维信号, Radon变换投影角度为30°.

对比图1(d)、图1(e)和图1(f)可以发现, 3种磨粒图像的归一化双谱幅值峰在双谱空间中出现的数量、位置以及峰值大小差异明显, 这也说明了根据磨粒图像的双谱, 提取磨粒的形状特征, 对磨粒进行识别是可行的.

2 基于形状标记的双谱分析

形状标记是将二维图像形状边界或区域用一维函数来表示的一种方法, 常用的形状标记方法有: 中心距离函数、面积函数、弦长函数、累积角函数、复坐标函数等. 近年来学者提出的形状标记方法有: 最远点距离函数^[8]、拱高半径复函数^[9]、周横截三角形面积函数^[10]等. 本文提出的基于形状标记的双谱分析方法, 首先计算磨粒形状的形状标记函数, 将二维图像转换为一维信号表示, 然后对得到的一维信号进行双谱分析, 最后得到磨粒形状的归一化双谱. 采用的形状标记方法有中心距离函数、累积角函数、最远点距离函数和三角形区域表示, 并且计算各形状标记时进行了归一化处理.

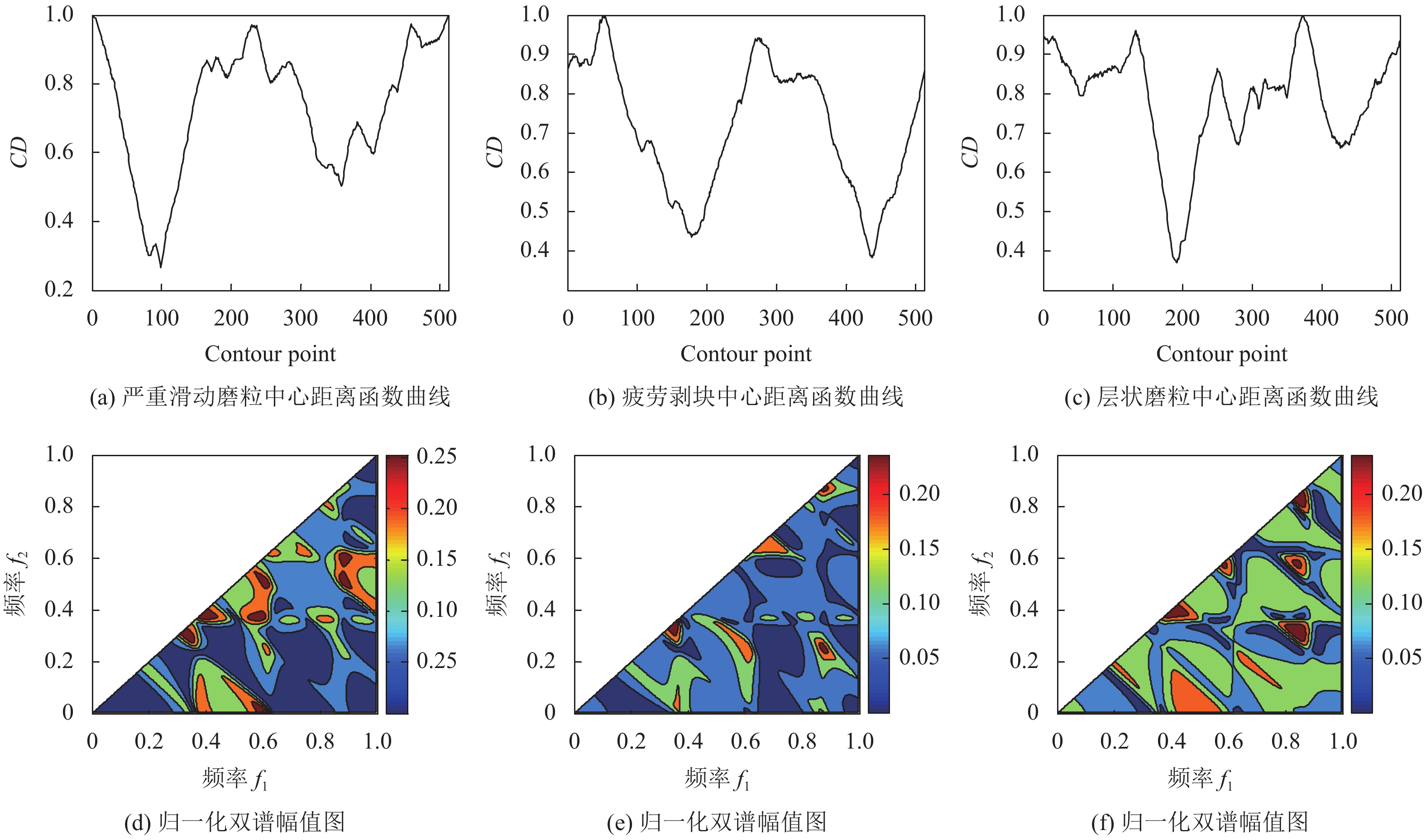
2.1 中心距离函数

中心距离函数(centroid distance)定义为形状轮廓点 $\left( {x(u),y(u)} \right)$ 和形状质心 $\left( {{x_c},{y_c}} \right)$ 之间的距离 $CD(u)$ :

$CD(u) = \sqrt {{{(x(u) - {x_c})}^2} + {{(y(u) - {y_c})}^2}} $

(6)

形状质心为:

${x_c} = \frac{1}{N}\sum\limits_{u = 0}^{N - 1} {x(u)} ,\;\quad {y_c} = \frac{1}{N}\sum\limits_{u = 0}^{N - 1} {y(u)} $

(7)

由中心距离函数的定义可以看出, 中心距离函数反映了形状的整体特征, 但是对形状的局部特征描述不足. 图2(a)、图2(b)、图2(c)分别为图1所示3种磨粒的中心距离函数曲线, 图2(d)、图2(e)、图2(f)分别为3种磨粒中心距离函数曲线的归一化双谱幅值图.

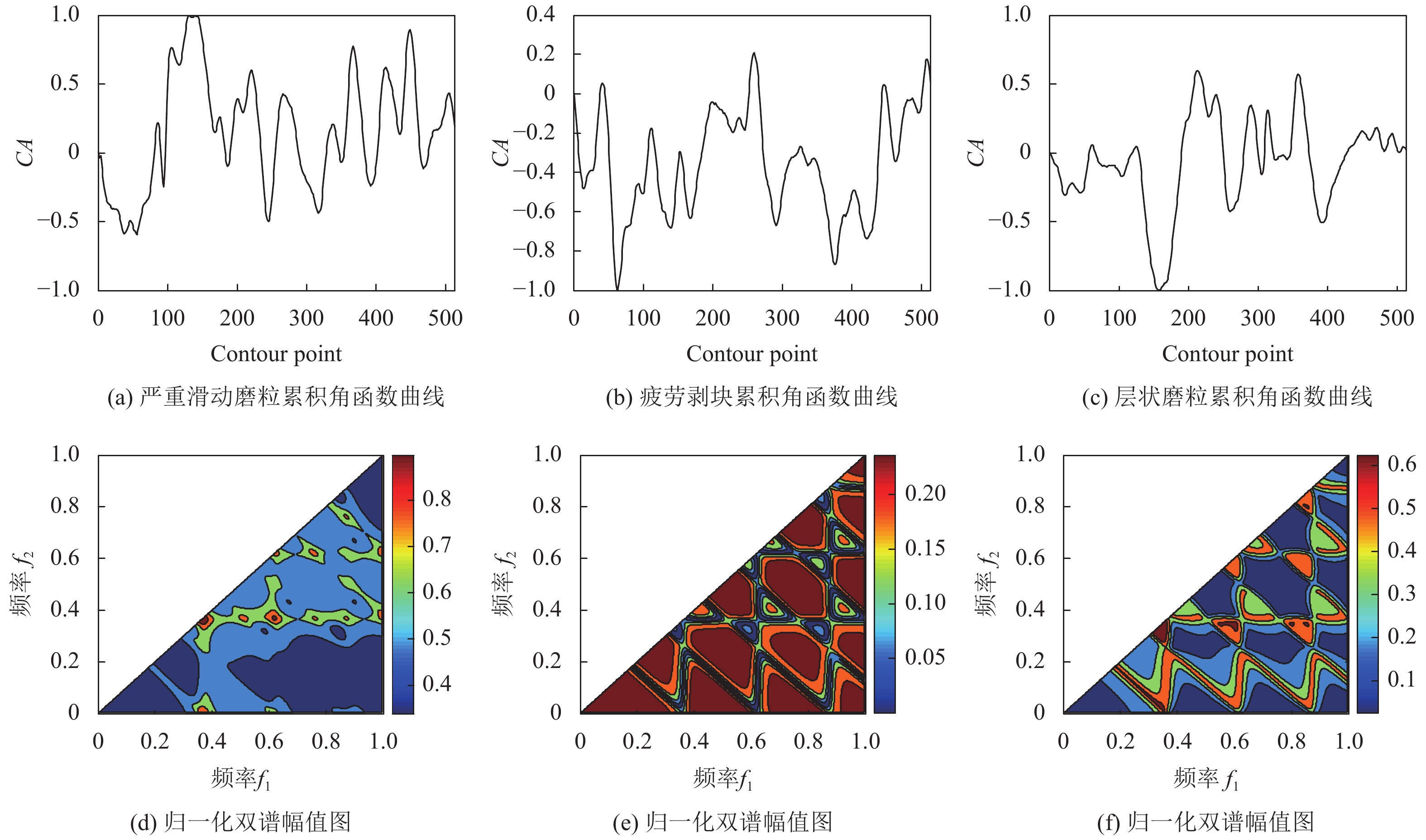
2.2 累积角函数

形状轮廓曲线的描述可以通过角函数 $\varphi (s)$ 参数化来实现, 定义的是正切线的角度方向. 但是角函数不具有连续性, 这是因为角度方向被限定在 $[0,2\pi ]$ 之间, 当角度方向大于或小于0时, 角函数具有不连续性. 这一问题通过Zahn和Roskie^[11]提出的累积角函数(cumulative angular function)的正规化形式得到了解决.

曲线上一点的累积角定义为从起始点开始的角度的变化量, 表示每个点角度变化的总和, 因此称为累积. 角度的变化由角函数 $\varphi (s)$ 的导数给出, 该导数与曲率 $k(s)$ 对应. 点的累积角函数定义为:

$CA(s) = \int_0^S {k(r)dr - k(0)} $

(8)

式中, 参数 $s$ 的取值范围为 $[0,L]$ , L为曲线的长度.

因此, 累积角函数的初始值和终点值分别为 $CA(0) = 0$ 和 $CA(L) = - 2\pi $ . 累积角函数虽然解决了角函数不连续的问题, 但是仍然存在两个问题, 它在终点不连续并且它的值取决于所分析曲线的长度. 这些问题通过定义正规函数 $C{A^*}(t)$ 来解决, $C{A^*}(t)$ 的定义为:

$C{A^*}(t) = CA\left( {\frac{L}{{2\pi }}t} \right) - t$

(9)

式中, $t$ 的取值范围为 $[0,2\pi ]$ , 系数 ${L / {2\pi }}$ 使得角函数正规化.

图3(a)、图3(b)、图3(c)分别为图1所示3种磨粒的累积角函数曲线, 图3(d)、图3(e)、图3(f)分别为3种磨粒的累积角函数曲线的归一化双谱幅值图.

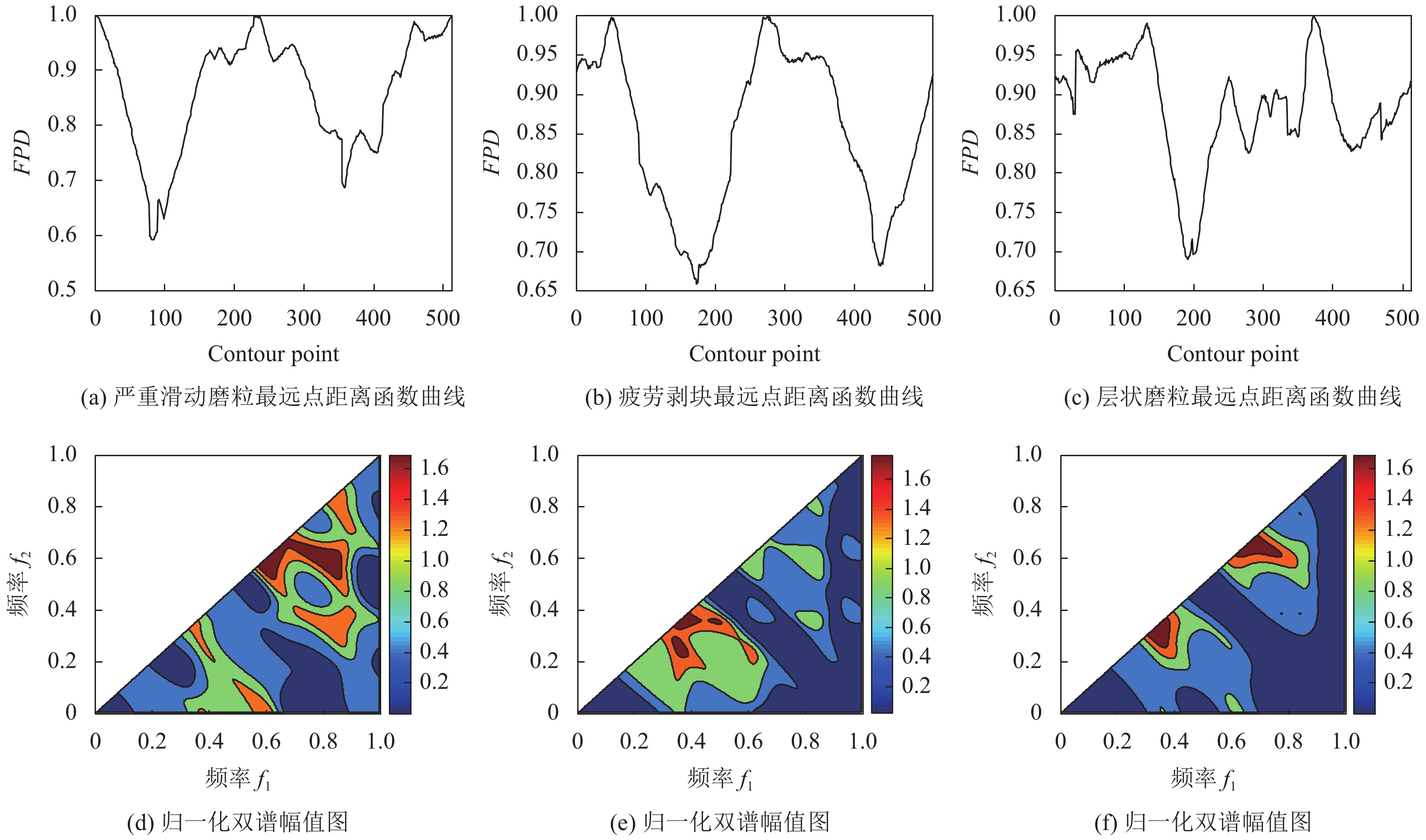
2.3 最远点距离函数

EL-ghazal等^[8]提出的最远距离函数方法(farthest point distance), 是指对于形状轮廓上的一点a, 在轮廓上找到与其距离最大的点b, 则a处的最远点距离函数值为点a与形状质心c的距离, 加上点a对应的最远点b与形状质心c的距离. 因此对于形状轮廓 $(x(u,y(u)),\; u = 0,1, \cdots ,N - 1$ , 最远点距离函数FPD定义为式(10).

$\begin{split} FPD(u) = &\sqrt {{{[x(u) - {x_c}]}^2} + {{[y(u) - {y_c}]}^2}} \\ & +\sqrt {{{[{x_{fp}}(u) - {x_c}]}^2} + {{[{y_{fp}}(u) - {y_c}]}^2}} \\ \end{split} $

(10)

式中, $({x_{fp}}(u),{y_{fp}}(u))$ 为轮廓点 $(x(u,y(u))$ 对应的最远点, $({x_c},{y_c})$ 为形状质心.

最远点距离函数旨在将轮廓的角点信息和轮廓细节信息加入到中心距离函数中, 用于克服中心距离函数对轮廓细节描述不足的缺点.

图4(a)、图4(b)、图4(c)分别为图1所示3种磨粒的最远点距离函数曲线, 图4(d)、图4(e)、图4(f)分别为3种磨粒最远点距离函数曲线的归一化双谱幅值图.

2.4 三角形区域表示

三角形区域表示(triangle area representation)^[12]根据形状轮廓上的点形成的三角形区域来进行计算, 可以用来度量轮廓点处的曲率. 对于轮廓上3个点 $(x(u - 1),y(u - 1))$ , $(x(u),y(u))$ 和 $(x(u + 1),y(u + 1))$ 所构成的三角形区域, 其面积 $TAR(u,k)$ 由下式计算得到:

$TAR(u) = \frac{1}{2}\det \left| {\begin{array}{*{20}{c}} {x(u - 1)}&{y(u - 1)}&1 \\ {x(u)}&{y(u)}&1 \\ {x(u + 1)}&{y(u + 1)}&1 \end{array}} \right|$

(11)

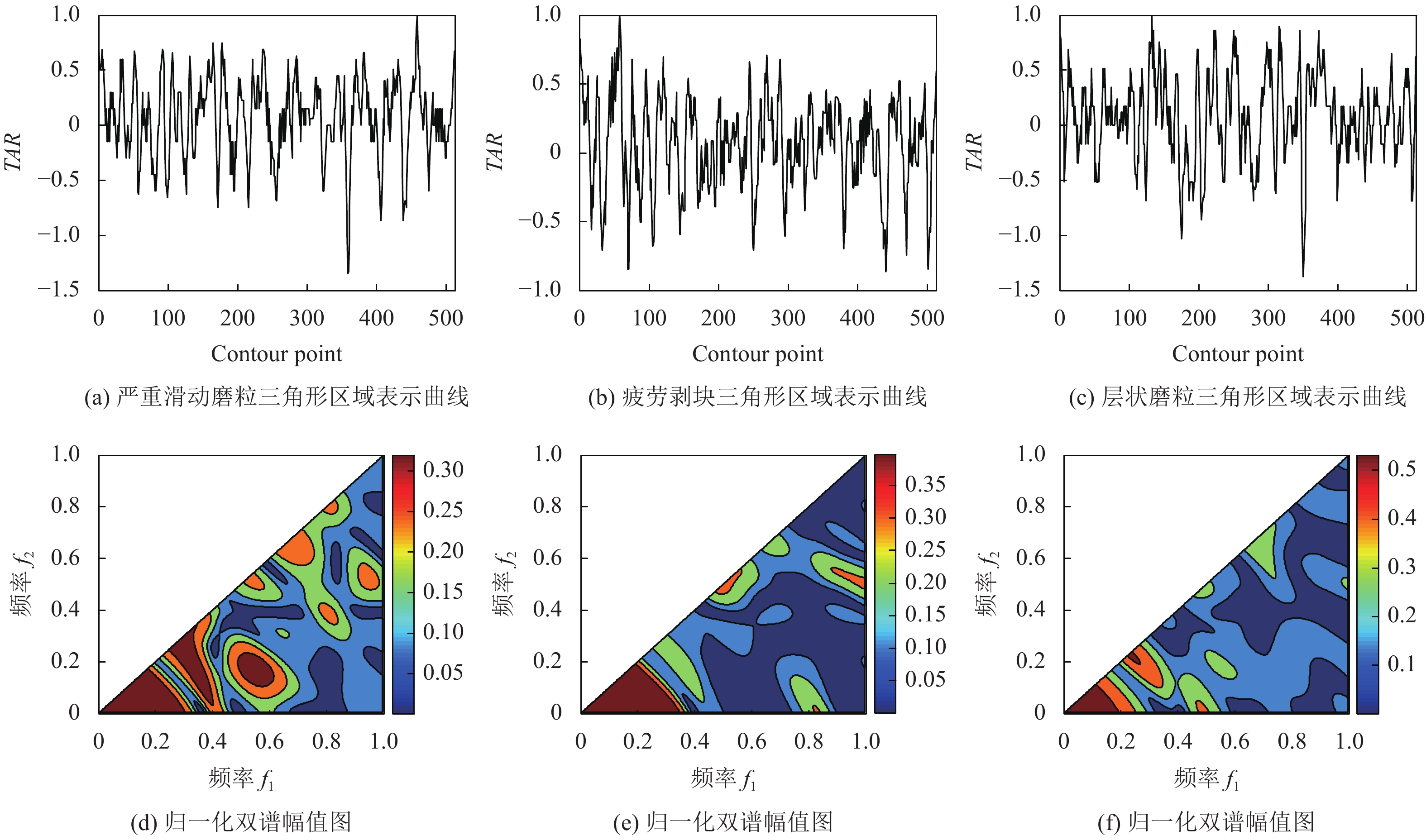
TAR取正值、负值和零值分别对应凸点、凹点和直线点, 表示每一个轮廓点的凹凸性, 图5(a)、图5(b)、图5(c)分别为图1所示3种磨粒的三角形区域表示曲线, 图5(d)、图5(e)、图5(f)分别为3种磨粒的三角形区域表示曲线的归一化双谱幅值图.

与根据Radon变换得到的归一化幅值图对比可以发现, 根据3种类型的磨粒形状标记得到的双谱幅值图, 双谱空间中峰出现的数量、位置以及峰值大小表现出的差异更加明显, 因此结合形状标记和双谱分析得到的形状特征区分能力更加有效.

3 基于形状标记的双谱分析 3.1 双谱不变量

双谱一般为复数, 具有幅值和相位, 即:

${B_x}({\omega _1},{\omega _2}) = \left| {{B_x}({\omega _1},{\omega _2})} \right|{e^{j{\phi _B}({\omega _1},{\omega _2})}}$

(12)

式中, $\left| {{B_x}({\omega _1},{\omega _2})} \right|$ 和 ${\phi _B}({\omega _1},{\omega _2})$ 分别为双谱的幅值和相位.

双谱具有如下对称性:

$\begin{split} & {B_x}({\omega _1},{\omega _2}) = {B_x}({\omega _2},{\omega _1}) = B_x^*( - {\omega _1}, - {\omega _2}) = B_x^*( - {\omega _2}, - {\omega _1}) \\ & \quad \quad \quad \quad \; = {B_x}( - {\omega _1} - {\omega _2},{\omega _2}) = {B_x}({\omega _1}, - {\omega _1} - {\omega _2}) \\ & \quad \quad \quad \quad \; = {B_x}( - {\omega _1} - {\omega _2},{\omega _1}) = {B_x}({\omega _2}, - {\omega _1} - {\omega _2}) \\ \end{split} $

(13)

双谱 ${B_x}({\omega _1},{\omega _2})$ 的对称线如图6所示, 有 ${\omega _1} = {\omega _2}$ , $2{\omega _1} = - {\omega _2}$ , $2{\omega _2} = - {\omega _1}$ , ${\omega _1} = - {\omega _2}$ , ${\omega _1} = 0$ 和 ${\omega _2} = 0$ . 双谱的定义域根据上述的对称线被划分成12个扇形区域. 图6中的阴影部分表示的三角形区域 ${\omega _2} \ge 0,{\omega _1} \ge {\omega _2},{\omega _1} + {\omega _2} \le \pi $ 为双谱 ${B_x}({\omega _1},{\omega _2})$ 在 $({\omega _1},{\omega _2})$ 平面内的主域, 由式(13)所示的双谱的对称性可知, 所有扇形区域的双谱能够根据主域内的双谱进行完全的描述.

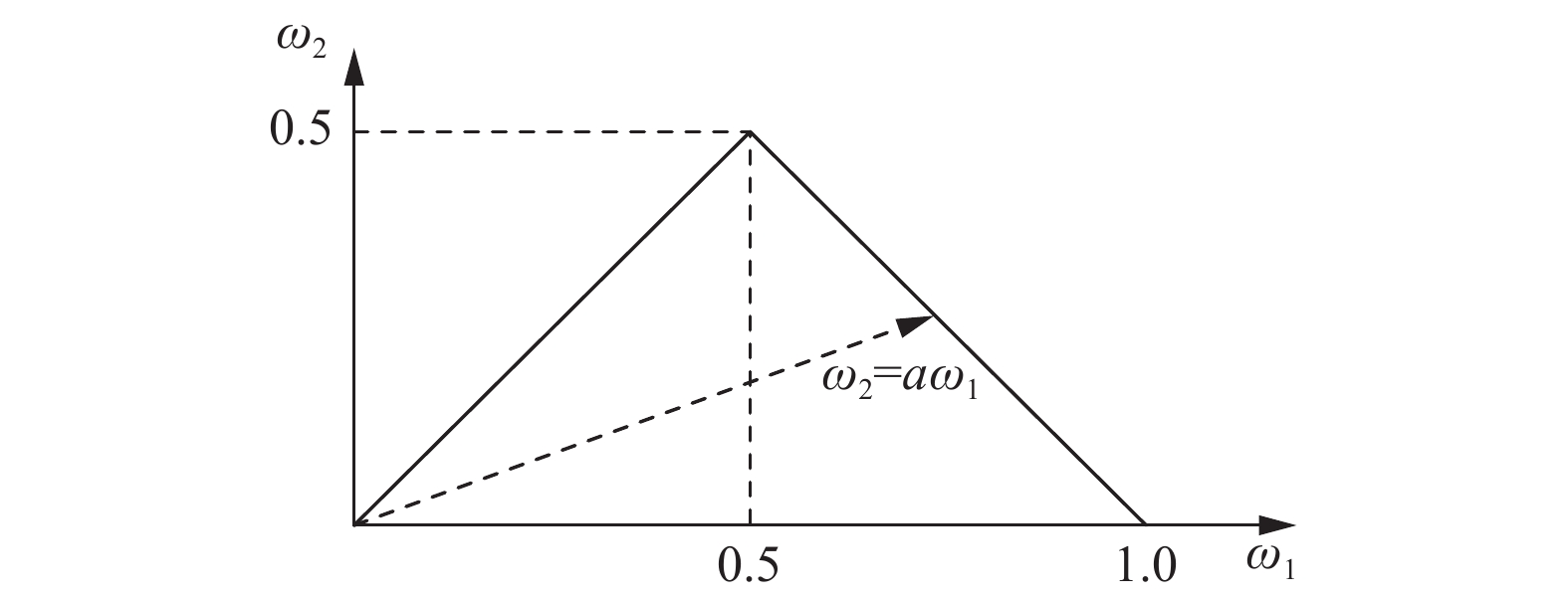
根据双谱的上述性质, 如图7所示在双谱主域内, 计算双谱不变量, 并以双谱不变量作为磨粒的形状特征. 本文在计算双谱不变量时, 采用两种方法: 一是根据双谱积分; 二是根据双谱矩.

根据双谱积分计算双谱不变量时, 在双谱主域内, 沿特定斜率 $a$ 的直线, 对双谱值进行积分得到 $I(a)$ , 以双谱值积分 $I(a)$ 的相位 $\phi (a)$ 作为双谱不变量:

$I(a) = \int\limits_{{\omega _1} = {0^ + }}^{\frac{1}{{1 + a}}} {{B_N}({\omega _1},a{\omega _1})d{\omega _1}} = {I_{{\rm{Re}} }}(a) + j{I_{{\rm{Im}} }}(a)$

(14)

$\phi (a) = \arctan \left( {\frac{{{I_{{\rm{Re}} }}(a)}}{{{I_{{\rm{Im}} }}(a)}}} \right)$

(15)

根据双谱矩计算双谱不变量时, 在双谱主域内计算归一化双谱的 $(p,q)$ 阶矩 $M(pq)$ , 以双谱矩 $M(pq)$ 的相位 $\phi (pq)$ 作为双谱不变量:

$M(pq) = \int {\int {\omega _1^p\omega _2^q{B_N}({\omega _1},{\omega _2})d{\omega _1}d{\omega _2}} } $

(16)

$\phi (pq) = \arctan \left( {\frac{{{M_{{\rm{Re}} }}(pq)}}{{{M_{{\rm{Im}} }}(pq)}}} \right)$

(17)

3.2 形状特征提取

本文采用双谱积分提取磨粒形状特征时, 斜率a的取值为 ${1 / {10}},{2 / {10}}, \cdots ,1$ , 则根据中心距离函数、累积角函数、最远点距离函数和三角形区域表示可分别得到10维形状特征, 分别为:

$\phi {a_{CDF}} = \left\{ { {\phi _{CDF}}\left( {\frac{1}{{10}}} \right),{\phi _{CDF}}\left( {\frac{2}{{10}}} \right), \cdots ,{\phi _{CDF}}(1)} \right\} $

(18)

$\phi {a_{CAF}} = \left\{ { {\phi _{CAF}}\left( {\frac{1}{{10}}} \right),{\phi _{CAF}}\left( {\frac{2}{{10}}} \right), \cdots ,{\phi _{CAF}}(1)} \right\} $

(19)

$\phi {a_{FPD}} =\left\{ {{\phi _{FPD}}\left( {\frac{1}{{10}}} \right),{\phi _{FPD}}\left( {\frac{2}{{10}}} \right), \cdots ,{\phi _{FPD}}(1)} \right\} $

(20)

$\phi {a_{TAR}} = \left\{ { {\phi _{TAR}}\left( {\frac{1}{{10}}} \right),{\phi _{TAR}}\left( {\frac{2}{{10}}} \right), \cdots ,{\phi _{TAR}}(1)} \right\} $

(21)

采用双谱矩提取磨粒形状特征时, $(p,q)$ 的阶数取值为(0,0), (0,1), (1,0), (1,1), (0,2), (2,0), (1,2), (2,1)和(2,2). 则根据中心距离函数、累积角函数、最远点距离函数和三角形区域表示可分别得到9维形状特征, 分别为:

$\phi p{q_{CDF}} = \left\{ { {\phi _{CDF}}(0,0),{\phi _{CDF}}(0,1), \cdots ,{\phi _{CDF}}(2,2)} \right\} $

(22)

$\phi p{q_{CAF}} = \{ {\phi _{CAF}}(0,0),{\phi _{CAF}}(0,1), \cdots ,{\phi _{CAF}}(2,2)\} $

(23)

$\phi p{q_{FPD}} = \{ {\phi _{FPD}}(0,0),{\phi _{FPD}}(0,1), \cdots ,{\phi _{FPD}}(2,2)\} $

(24)

$\phi p{q_{TAR}} = \{ {\phi _{TAR}}(0,0),{\phi _{TAR}}(0,1), \cdots ,{\phi _{TAR}}(2,2)\} $

(25)

根据以上分析, 结合中心距离函数、累积角函数、最远点距离函数、三角形区域表示和双谱分析, 通过双谱积分和双谱矩计算双谱不变量, 以双谱不变量作为磨粒的形状特征, 共可以得到76维形状特征F:

$\begin{array}{l} F = \{ \phi {a_{CDF}},\phi {a_{CAF}},\phi {a_{FPD}},\phi {a_{TAR}}, \\ \quad \quad \phi p{q_{CDF}},\phi p{q_{CAF}},\phi p{q_{FPD}},\phi p{q_{TAR}}\} \\ \end{array} $

(26)

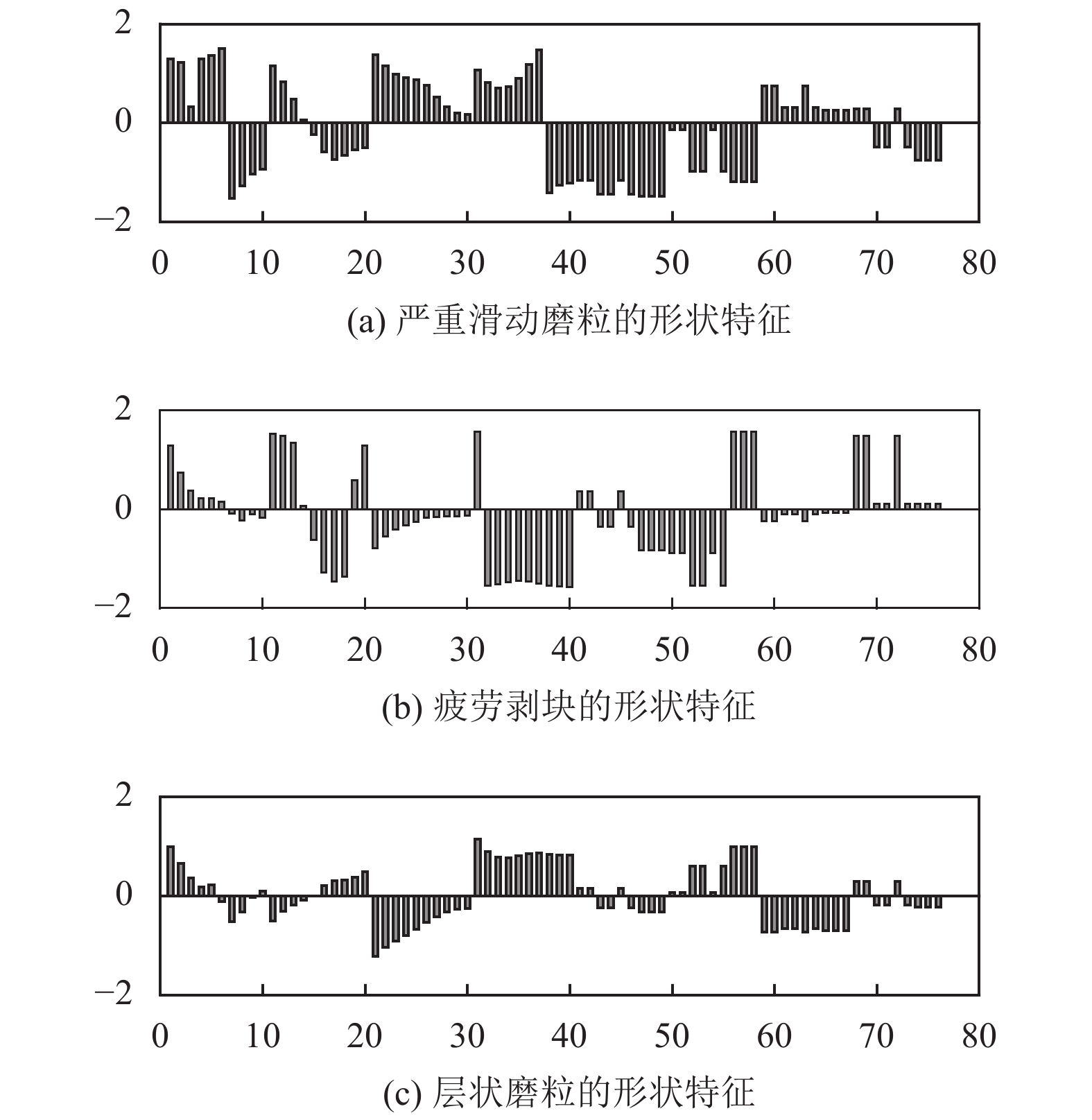
图8为以直方图表示的, 采用本文方法得到的图1所示的3种类型磨粒的形状特征, 直方图的前40个分量为结合中心距离函数、累积角函数、最远点距离函数、三角形区域表示和双谱分析, 通过双谱积分得到的形状特征, 后36个分量为通过双谱矩得到的形状特征. 观察图8可以发现, 3种类型的磨粒采用本文方法得到的形状特征区别明显, 在采用每种形状标记和双谱分析得到的形状特征分量上都表现出了差别.

4 实验结果与分析 4.1 实验设计

为了有效评价所提出的形状特征提取算法的有效性, 本文将所提出的算法在形状识别领域应用广泛的MPEG-7 CE Shape-1 Part B^[13]数据集和Swedish leaf^[14]数据集上进行实验与分析, 并与其它方法进行对比.

本文实验中主要与几种形状标记的方法进行比较, 参与比较的形状特征提取方法包括: 文献[5]的方法、文献[15]的方法和文献[16]的方法. 其中文献[5]的方法是通过Radon变换将图像映射到一组一维投影, 然后对一维信号进行双谱分析得到形状特征; 文献[15]的方法是根据轮廓的多尺度拱高作为形状特征; 文献[16]的方法是根据轮廓的多尺度弹性度作为形状特征. 以上3种方法中, 第一种为采用Radon变换和双谱分析相结合的方法, 后两种都是多尺度形状标记的方法.

4.2 实验过程

为了综合评价各形状特征提取算法的性能, 本文中进行两组实验, 实验1是在原始数据集上进行的, 实验2是在添加高斯噪声的数据集上进行的. 在实验2中, 为了评价各形状特征提取算法的抗噪声干扰能力, 在MPEG-7数据集和Swedish leaf数据集的每幅图片上添加均值为0, 标准差为σ的高斯噪声, 其中σ的取值由0.1变化到1. 由于文献[15]的方法、文献[16]的方法和本文方法都是根据形状轮廓提取形状特征, 因此对图像添加噪声时, 是在形状轮廓的像素上添加高斯噪声, 而文献[5]的方法是根据形状区域提取形状特征, 因此对图像添加高斯噪声时, 是在整幅图像上添加的. 为了便于对各种方法进行比较, 根据本文方法和文献中的方法进行形状识别时, 分类器采用k近邻法, 用留一法交叉验证各形状特征提取方法的性能, 以识别准确率作为评价指标.

4.3 实验结果

实验1的结果如表1所示, 由表1所示的实验结果可以看出, 在MPEG-7数据集和Swedish leaf数据集上, 本文方法和两种多尺度形状标记的方法识别准确率都比较高, 其中文献[16]方法的识别准确率最高, 文献[5]方法得到识别率最低.

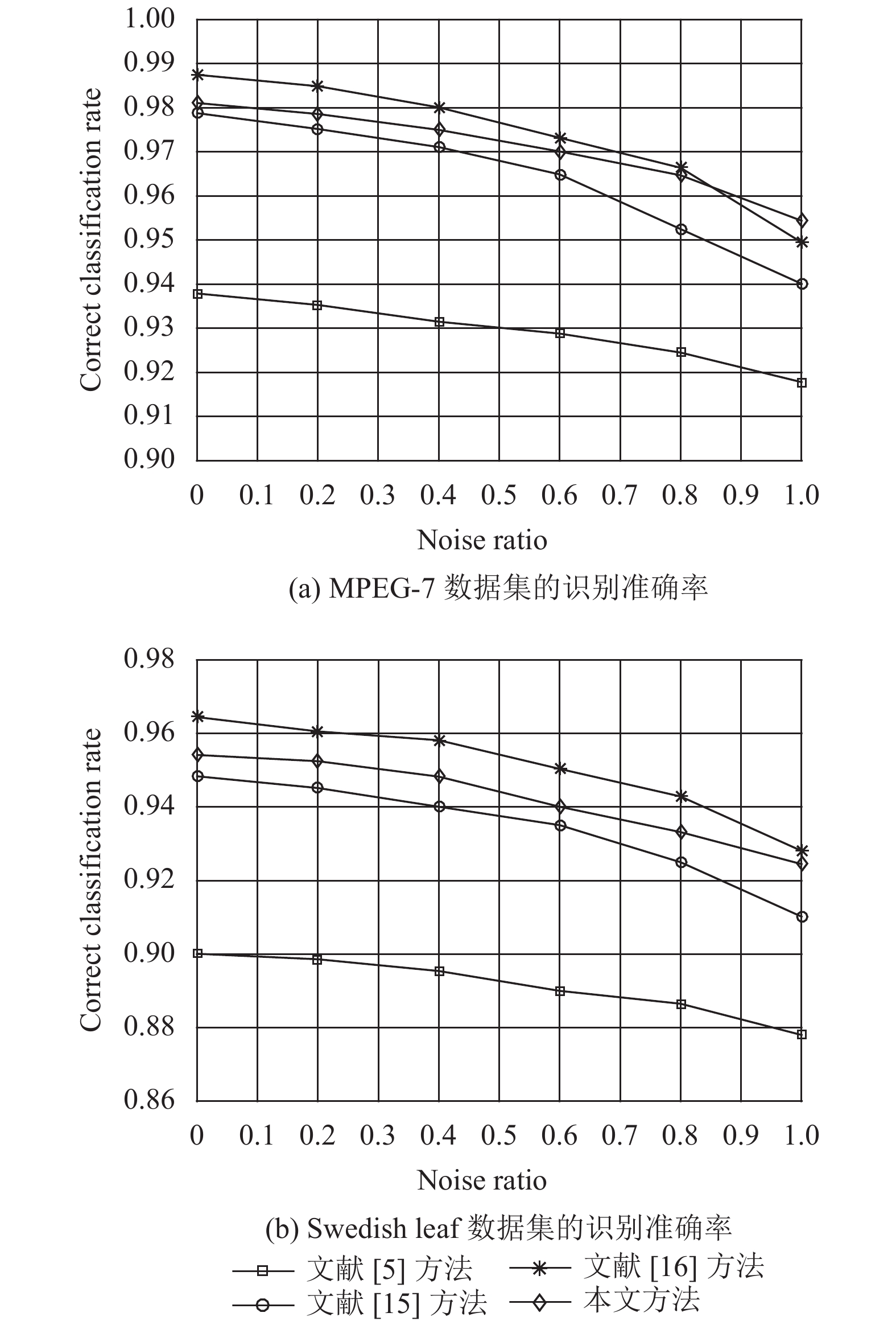
实验2所得实验结果如图9所示. 由图9(a)和图9(b)的对比可以看出, 随噪声水平的增加, 各算法识别准确率在MPEG-7数据集和Swedish leaf数据集上的变化趋势大致相同, 与文献[15]的方法和文献[16]的方法相比, 本文方法和文献[5]的方法随噪声水平的增加, 识别准确率的变化相对较小.

4.4 结果分析

由以上两个实验看出, 在文献[5]方法的基础上, 本文利用形状标记方法将二维图像转换成一维信号, 然后对其进行双谱分析, 以双谱不变量作为形状特征, 可以提高双谱分析用于形状识别时的识别准确率, 同时与基于形状标记的形状特征提取算法相比, 可以显著提高对噪声的抗干扰能力.

5 总结

本文结合形状标记和双谱分析用于提取图像的形状特征. 首先采用4种形状标记方法: 中心距离函数、累积角函数、最远点距离函数和三角形区域表示, 将二维图像转换为一维信号表示; 然后对得到的一维信号进行双谱分析, 得到形状的归一化双谱; 最后在归一化双谱域内, 根据双谱积分和双谱矩计算双谱不变量, 作为图像的形状特征, 共计76维. 为了有效评价所提方法的有效性, 在MPEG-7 CE Shape-1 Part B数据集和Swedish leaf数据集上进行形状识别能力实验与抗噪声能力实验. 实验结果表明: 本文所提方法能够有效提高双谱分析用于形状识别时的识别准确率, 同时与基于形状标记的形状提取方法相比, 能够显著提高抗噪声干扰能力.