近年来, 目标跟踪在视频监控、运动分析、人机交互、自动驾驶及交通安防等领域获得了长足发展. 但大多数目标跟踪算法不但在面对光照变化、运动模糊、快速运动、背景混乱、遮挡等复杂环境下跟踪失败, 而且在目标变形、旋转、姿势变化等剧烈变化时也表现欠佳. 因此, 有必要继续探索健壮的目标跟踪算法.

以往研究表明, 有效的特征一般能较好的表示跟踪目标并快速运算, 代表性的有颜色特征^[1]、纹理特征^[2]、灰度特征^[3]、超像素特征^[4]、Lab特征^[5]等. 得益于特征引入频域, 将矩阵乘法运算转化为点乘运算, 基于相关滤波的目标跟踪算法获得了长足发展. 譬如: 基于单通道灰度特征的MOSSE^[6]和CSK^[7]、基于11通道颜色特征的CN^[8]、基于31通道HOG特征的KCF^[9]、基于42通道特征(31维HOG特征、10维颜色特征、1维灰度特征)的SAMF^[10]、基于HOG特征和颜色特征的Staple^[11]、基于HOG特征和Lab特征的SACFT^[12]等. 这些算法一般将不同特征简单叠加或以固定比例组合, 未考虑实时特征组合对目标跟踪的影响. 针对该问题, 赵高鹏等^[13]基于峰值旁瓣比融合灰度特征和LBP特征, 陈法领等^[14]基于峰值旁瓣比和相邻帧间的响应一致性融合纹理特征和颜色特征, 尹宽等^[15]基于融合特征器的可信度选择合适线性组合方式, 常敏等^[16]基于平均峰值-相关能量方法融合不同特征. 与几位学者从特征类别层面融合特征的做法不同, 本文算法从特征通道层面融合特征, 该算法通过各通道对响应值的贡献度调整权重, 构建实时特征组合, 进而控制特征融合, 从而提升跟踪效果.

本文算法的亮点主要表现在以下几个方面: (1)引入通道权重矩阵, 不破坏循环矩阵性质, 不影响闭合求解; (2)先对特征矩阵和权重矩阵点乘, 不影响框架将矩阵乘运算转化到傅里叶域下求点乘; (3)基于各通道响应值构建权重更新策略, 及时捕捉目标运动状态, 灵活构建特征组合.

相关实验结果表明: 通道权重在特征融合过程中, 发挥着很大的作用; 本文提出的特征融合算法在跟踪目标时能有效提升精确度和成功率.

1 基于通道权重融合特征的目标跟踪算法

为了能够使用多维度特征, Galoogahi等^[17]提出多通道相关滤波算法. 该算法设定:

$\begin{split} E({{h}}) =& \dfrac{1}{2}\displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{j = 1}^D {\left\| {{y_i}(j) - \displaystyle\sum\nolimits_{k = 1}^K {{h^{(k)}}^{\rm{T}} * x_{_i}^k\left[ {\Delta {\tau _j}} \right]} } \right\|}_2^2 } \\ &+\dfrac{\lambda }{2}\displaystyle\sum\limits_{k = 1}^K {\left\| {{h^{(k)}}} \right\|} _2^2 \end{split} $

(1)

式中, N是样本数目, D是循环移位的位数, ${y_i}(j)$ 是期望相关响应的第j个元素, K是特征通道数目, ${{{h}}^{(k)}}$ 是第k通道的过滤器, $x_{_i}^k$ 是第i帧第k通道的向量化, $\Delta {\tau _j}$ 表示循环位移操作, $x_{_i}^k\left[ {\Delta {\tau _j}} \right]$ 是对 $x_{_i}^k$ 做j步的循环位移, $\lambda $ 是规范化系数.

在跟踪过程中, 各个通道对响应值的贡献度不同, 而该算法将各通道等同看待. 因此, 提出基于通道融合特征的目标跟踪算法. 该算法的目标函数如下:

$ \begin{split} E({{h}}) =& \dfrac{1}{2}\displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{j = 1}^D {\left\| {{y_i}(j) - \displaystyle\sum\nolimits_{k = 1}^K {{{{h}}^{(k)}}^{\rm{T}} * (ratio_i^k * x_{_i}^k)\left[ {\Delta {\tau _j}} \right]} } \right\|} _2^2}\\ &+\dfrac{\lambda }{2}\displaystyle\sum\limits_{k = 1}^K {\left\| {{h^{(k)}}} \right\|} _2^2 \end{split} $

(2)

式中, N、D、 ${y_i}(j)$ 、K、 $ratio_i^k$ 、 ${{{h}}^{(k)}}$ 、 $x_{_i}^k$ 、 $\Delta {\tau _j}$ 、 $\lambda $ 同式(1)中变量意义相同, $(ratio_i^k * x_{_i}^k)\left[ {\Delta {\tau _j}} \right]$ 是对 $(ratio_i^k * x_{_i}^k)$ 做j步的循环位移.

1.1 引入特征权重

与式(1)相比, 式(2)中添加了 $ratio_i^j$ . 该项通过各通道响应值占比(见式(3))构建, 与 $x_{_i}^k\left[ {\Delta {\tau _j}} \right]$ 相乘实现自适应特征组合, 一定程度上发挥着特征权重的作用. 具体实现如下:

$ratio_i^k{\rm{ = }}\left\{ \begin{array}{l} {{f}}_i^k{\rm{/}}\displaystyle\sum\limits_{k = 1}^K {{{f}}_i^k} {\rm{, }}\;\displaystyle\sum\limits_{k = 1}^K {{{f}}_i^k} > 0,\;0 < j < K + 1 \\ 0,\;{\rm{ otherwise}} \\ \end{array} \right.$

(3)

式中, $ratio_i^k$ 是第i帧第k通道的响应值占比, ${{f}}_i^k$ 表示第i帧第k通道的响应值, K是特征通道数目, $\displaystyle\sum\limits_{k = 1}^K {{{f}}_i^k}$ 表示第i帧的所有通道响应值之和.

1.2 引入区域评估机制

为保证 $ratio_i^j$ 的准确性, 对式(3)中的 ${{f}}_i^k$ 引入区域评估机制. 该机制基于一个前提和一个区域特性. 该前提设定如下:

$ \begin{array}{l} (po{s_m},po{s_n}) = \mathop {\arg \max }\limits_{(po{s_m},po{s_n})} \displaystyle\sum\limits_{k = 1}^K {{{f}}_i^k(m,n)} ,\\ 0 < m < M + 1,0 < n < N + 1 \end{array} $

(4)

式中, $(po{s_m},po{s_n})$ 是最佳坐标位置, M是搜索区域的宽度, N是搜索区域的高度, ${{f}}_i^k(m,n)$ 是第i帧第k通道 $(m,n)$ 处的响应值.

由于 $\displaystyle\sum\limits_{k = 1}^K {{{f}}_i^k(po{s_m},po{s_n})}$ 最大, 并不能保证 ${{f}}_i^k(po{s_m}, po{s_n})$ 在第i帧第k通道上也是最大值. 但是, 如果 ${{f}}_i^k (po{s_m},po{s_n})$ 在第i帧第k通道上, 小于甚至等于 ${\rm{(}}po{s_m}, po{s_n}{\rm{) }}$ 周围8个位置上的最大响应值, 那么该通道上的位置选择一定是错误的. 所以, 该通道上的响应值 ${{f}}_i^k(po{s_m},po{s_n})$ 对特征组合的贡献度应该为零, 这就是有效通道的区域特性. 而该特性也在一定程度上保证了模型推测的位置至少是在各个通道上是局部最优, 也就是 ${{f}}_i^k(po{s_m},po{s_n})$ 大于 ${\rm{(}}po{s_m},po{s_n}{\rm{) }}$ 周围8个位置上的最大响应值. 该区域特性具体实现如下:

$ \left\{\begin{split} &{{{f}}_{\max }} = \arg \max ({{f}}_i^k{\rm{(}}po{s_{m - 1:m + 1}},po{s_{n - 1:{{n}} + 1}}{\rm{) )}}\\ &{{f}}_i^k{\rm{ = }}\left\{ \begin{array}{l} {\rm{ }}{{f}}_i^k{\rm{(}}po{s_m},po{s_n}{\rm{) , }}\;{{f}}_i^k{\rm{(}}po{s_m},po{s_n}{\rm{) }} > {{{f}}_{\max }}{\rm{ }} \\ {\rm{0 , }}\;{\rm otherwise} \\ \end{array} \right. \end{split}\right. $

(5)

式中, ${{f}}_i^k$ 表示第i帧第k通道的响应值, ${\rm{(}}po{s_m},po{s_n}{\rm{) }}$ 表示模型推测的位置, ${\rm{(}}po{s_{m - 1:m + 1}},po{s_{n - 1:{{n}} + 1}}{\rm{) }}$ 表示 ${\rm{(}}po{s_m}, po{s_n}{\rm{) }}$ 的上、下、左、右、左上、右上、左下和右下共8个位置, ${{{f}}_{\max }}$ 表示第i帧第k通道 ${\rm{(}}po{s_m},po{s_n}{\rm{) }}$ 周围8个位置的最大响应值.

1.3 引入滑动窗口机制

式(2)的 $(ratio_i^k * x_{_i}^k)\left[ {\Delta {\tau _j}} \right]$ 将被拓展转化为 ${{{X}}_\beta }$ (见式(7)有关说明), 构成模型 ${\hat {{\alpha}} _i}$ 的组成部分. 而 ${\hat {{\alpha}} _i}$ 的更新被设定为线性递增, 为了保持 $ratio_i^k$ 与 ${\hat \alpha _i}$ 的同步, $ratio_i^k$ 也被设定为线性递增.

由于式(5)中的 ${{f}}_i^k$ 均大于等于0, 造成 $ratio_i^k$ 均大于等于0. 长期跟踪过程中, 一些通道的权重值将迅速累加, 势必造成模型严重依赖个别通道, 这对模型非常不利.

为缓解这一问题, 引入滑动窗口机制. 该机制限定模型仅依据当前帧及其以前的部分帧, 来更新通道权重. 在减缓通道特征累加风险的同时, 捕捉最近的模型变化, 舍弃较久远的变化. 该机制设定如下:

$ratio_{I + 1}^k{\rm{ = }}\left\{ \begin{array}{l} ratio_0^k{\rm{ + }}rati{o^w}{\rm{*}}\displaystyle\sum\limits_{i = 1}^I {ratio_i^k},\; 0 < I < n + 1 \\ ratio_0^k{\rm{ + }}rati{o^w}{\rm{*}}\displaystyle\sum\limits_{i = i - 99}^I {ratio_i^k} {\rm{ , }}\;n < I \\ \end{array} \right.$

(6)

式中, $ratio_{I + 1}^k$ 是第I+1帧第k通道的权重, $ratio_0^k$ 是第k通道的初始值, $rati{o^w}$ 是权重学习率, $ratio_i^k$ 是第i帧第k通道的权重, n是参与权重更新的帧数目.

2 算法实现

目标函数式(2)可以化简为:

$\frac{1}{2}\left\| {y - {X_\beta }\omega } \right\|_2^2 + \frac{\lambda }{2}\left\| \omega \right\|_2^2$

(7)

式中, $y$ 是回归目标 ${{{y}}_i}$ 的集合, ${{{X}}_\beta }$ 是 $({({{X}}_\beta ^1{\rm{)}}^{\rm T}}{({{X}}_\beta ^2{\rm{)}}^{\rm T}} \cdots {({{X}}_\beta ^k{\rm{)}}^{\rm T}}\cdots {({{X}}_\beta ^K{\rm{)}}^{\rm T}})^{\rm T}$ , $({{X}}_\beta ^k{\rm{)}}$ 是 $(ratio_i^k * x_{_i}^k)\left[ {\Delta {\tau _j}} \right]$ 的循环矩阵, $\omega $ 是线性回归方程的投影矩阵.

2.1 求解线性回归

求解式(7)得:

${{\omega}} = {\rm{ }}{\left( {{{\left( {{{{X}}_\beta }} \right)}^{\rm T}}{{{X}}_\beta } + \lambda I} \right)^{ - 1}}{\left( {{{{X}}_\beta }} \right)^{\rm T}}y$

(8)

式中, ${{X}}$ 、 ${{{X}}_\beta }$ 、 $y$ 同式(7)中对应变量意义相同, I是单位矩阵.

在复数空间的傅里叶域下:

${{\omega}} = {\rm{ }}{\left( {{{({{{X}}_\beta })}^{\rm H}}{{{X}}_\beta } + \lambda {{I}}} \right)^{ - 1}}{({{{X}}_\beta })^{\rm H}}{{y}}$

(9)

式中, ${{{X}}^{\rm H}}$ 是X的复共轭转置, ${{{X}}^{\rm H}} = {({{{X}}^*})^{\rm T}}$ .

2.2 求解非线性回归

引入核机制^[9], 将线性问题的输入映射到非线性空间 ${{\varphi}} \left( {{x}} \right)$ , 则 ${{\omega}}$ 可以表示为:

${{\omega}} = \sum\limits_{{i}} {{{{\alpha}} _i}{{\varphi}} \left( {{{{x}}_i}} \right)} $

(10)

式中, ${{\alpha}}$ 是对偶空间.

将 $f({\textit{z}}) = {{{\omega}} ^{\rm T}}{\textit{z}} = \displaystyle\sum\limits_i^n {{{{\alpha}} _i}k({\textit{z}},{{{x}}_i})}$ 带入式(7), 求解得:

${{\alpha}} = {({{K}} + \lambda {{I}})^{ - 1}}y$

(11)

式中, ${{{K}}_{ij}}{\rm{ = }}k\left( {{{({{{x}}_\beta })}_i},{{({{{x}}_\beta })}_j}} \right) = {\varphi ^{\rm T}}\left( {{{({{{x}}_\beta })}_i}} \right)\varphi \left( {{{({{{x}}_\beta })}_j}} \right)$ .

在傅里叶域下, 有:

$\hat {{\alpha}} = \frac{{\hat {{y}}}}{{{{\hat {{k}}}^{{x_\beta }{x_\beta }}} + \lambda }}$

(12)

式中, 帽 $ \wedge $ 表示对应的离散傅里叶变换.

2.3 核函数选择

选择高斯核^[9]:

$ \begin{split} {{{k}}^{{x_\beta } {x_\beta }'}}\!\!\! =\! \exp \left(\! { - \frac{1}{{{\delta ^2}}}\left( {{\left\| {{{{x}}_\beta }} \right\|^2} + {\left\| {{{{x}}_\beta }'} \right\|^2}}\! \right)}\!- \!{ 2{{\cal{F}}^{ - 1}}\left({{\sum\limits_{j = 1}^C {{{\left(\hat x_\beta ^j\right)}^*} \odot }}\left( \hat x_\beta ^j\right)'}\right)} \right) \end{split} $

(13)

选择线性核^[9]:

${{{k}}^{{x_\beta } {x_\beta }'}} = \exp \left( - 2{{\cal{F}}^{ - 1}}{\left(\sum\limits_{j = 1}^C {{{(\hat x_\beta ^j)}^*} \odot (} \hat x_\beta ^j)'\right)}\right)$

(14)

式中, C表示特征通道数目.

2.4 检测阶段

选择高斯核^[9]:

$ {k^{{x_\beta } {{\textit{z}}_\beta }}} = \exp \left( { - {\frac{1}{\delta ^2}}\left( {\left\| {x_\beta} \right\|^2} + {\left\| {\textit{z}}_\beta \right\|^2} \right) -{2{\cal{F}}^{ - 1}\left(\displaystyle\sum\limits_{j = 1}^C {{{\left(\hat x_\beta ^j\right)}^*} \odot \hat {\textit{z}}_\beta ^j} \right)}} \right) $

(15)

选择线性核^[9]:

${{{k}}^{{x_\beta } {{\textit{z}}_\beta }}} = \exp \left( - 2{{\cal{F}}^{ - 1}}\left(\sum\limits_{j = 1}^C {{{(\hat {{x}}_\beta ^j)}^*} \odot \hat {\textit{z}}_\beta ^j} \right)\right)$

(16)

其中, ${{{\textit{z}}}}$ 为样本的特征矩阵, ${{{{\textit{z}}}}_\beta } = {\textit{z}} \odot \beta $ , ${{{\textit{z}}}}_\beta ^j$ 表示对 ${{{\textit{z}}}}$ 的第j通道施加特征权重, C表示特征通道数目.

$f\left( {\textit{z}} \right) = {{\cal{F}}^{ - 1}}\left( {{{\hat {{k}}}^{{x_\beta }{{\textit{z}}_\beta }}} \odot \hat {{\alpha}} } \right){\rm{ = }}{{\cal{F}}^{ - 1}}\left( {\frac{{{{\hat {{k}}}^{{x_\beta }{{\textit{z}}_\beta }}} \odot \hat {{y}}}}{{{{\hat {{k}}}^{{x_\beta }{x_\beta }}} + \lambda }}} \right)$

(17)

式中, $f\left( {{{\textit{z}}}} \right)$ 表示样本特征 ${{{\textit{z}}}}$ 的响应值, ${{\cal{F}}^{ - 1}}$ 表示反傅里叶变换, 帽 $ \wedge $ 表示对应的离散傅里叶变换.

2.5 更新阶段

根据式(3)、式(5)、式(6)更新 $ratio_i^k$ , 并将 $ratio_i^k$ 代入式(12)得到 ${\hat {{\alpha}} _i}$ , 进一步更新模型:

${\hat {{\alpha}} _i} = (1 - lr)*{\hat {{\alpha}} _{i - 1}} + lr*{\hat {{\alpha}} _i}$

(18)

式中, ${\hat {{\alpha}} _i}$ 是跟踪第i帧后更新的模型, ${\hat {{\alpha}} _{i - 1}}$ 是跟踪第i–1帧后更新的模型, $lr$ 是模型学习率.

2.6 算法流程

具体算法流程如算法1所示.

算法1. 本文算法

输入: 视频序列 $\scriptstyle Fram{e_1}$ , $\scriptstyle Fram{e_{\rm{2}}}$ , …, $\scriptstyle Fram{e_{{N}}}$ ,回归目标 $\scriptstyle {{y}} \in {R^{{{m}} \times {{n}}}}$ , 初始帧的目标中心位置 $\scriptstyle ce{n_0}$ .

输出: 当前帧curframe的目标中心位置 $\scriptstyle ce{n_{\rm curframe}}$ .

For $\scriptstyle {{ 1:N}}$

IF $\scriptstyle frame > 0$

① 在前一帧preframe目标中心位置 $\scriptstyle ce{n_{\rm preframe}}$ 的周围, 划定检测区域并采集样本;

② 对采集到的样本提取纹理特征 $\scriptstyle {{{Z}}_{\rm hog}} \in {R^{m \times n \times 31}}$ 、颜色特征 $\scriptstyle {{{Z}}_{\rm color}} \in {R^{m \times n \times 10}}$ 和灰度特征 $\scriptstyle {{{Z}}_{\rm grey}} \in {R^{m \times n \times 1}}$ , 对特征 $\scriptstyle {{{Z}}_{\rm cur}} = [{{{Z}}_{\rm hog}},{{{Z}}_{\rm color}},$ $\scriptstyle {{{Z}}_{\rm grey}}] \in {R^{m \times n \times 42}}$ 执行 $\scriptstyle {{{Z}}_\beta } = {{{Z}}_{\rm cur}} \odot {\scriptstyle {\beta}}$ 操作, 再对 $\scriptstyle {{{Z}}_\beta }$ 做FFT, 得到频域特征 $\scriptstyle {\hat {{Z}}_\beta }$ ;

③ 使用高斯核时, 利用式(13)、式(15)、式(17)求响应值 $\scriptstyle f\left( {\textit{z}} \right)$ ; 使用线性核时, 利用式(14)、式(16)、式(17)求响应值 $\scriptstyle f\left( {\textit{z}} \right)$ ;

④ $\scriptstyle ce{n_{\rm curframe}} = \mathop {\arg \max }\limits_{{\rm{(}}po{s_m},po{s_n}{\rm{) }}} (f({\textit{z}}))$

End

⑤ 利用式(3)、式(5)、式(6)更新通道权重;

⑥ 使用高斯核时, 利用式(15)、式(12)、式(18)更新外观模型; 使用线性核时, 利用式(16)、式(12)、式(18)更新外观模型;

End

3 实验结果与分析 3.1 实验数据

实验选取了公开数据集OTB-2015^[18]的100组视频序列, 围绕光照变化(Illumination Variation, IV)、尺度变化(Scale Variation, SV)、遮挡(Occlusion, OCC)、变形(Deformation, DEF)、运动模糊(Motion Blur, MB)、快速运动(Fast Motion, FM)、平面内旋转(In-Plane Rotation, IPR)、平面外旋转(Out-of-Plane Rotation, OPR)、超出视野范围(Out-of-View, OV)、背景杂乱(Background Clutters, BC)、低分辨率(Low Resolution, LR)等11种挑战情况进行展开.

3.2 评价指标

本文主要用到3个评价指标, 分别是精确度(precision)、成功率(success rate)和跟踪速度(speed). 精确度是在跟踪序列中准确跟踪到的帧所占的比重, 这些帧的目标中心与真实位置的距离小于某个阈值, 该指标越大越好; 成功率是在跟踪序列中准确跟踪到的帧所占的比重, 这些帧的跟踪框与真实框的重叠率大于某个阈值, 该指标越大越好; 跟踪速度是每秒跟踪的帧数, 一般采用帧/秒(fps)表示.

(1)精确度

精确度求解如下:

$pre(j){\rm{ = }}\dfrac{{\displaystyle\sum\limits_{i = 1}^{frames} {1\left\{ {\sqrt {{{\left( {x_i^T - x_i^G} \right)}^2} + {{\left( {y_i^T - y_i^G} \right)}^2}} \le \varepsilon (j)} \right\} } }}{{frames}}$

(19)

式中, $pre(j)$ 是阈值取 $\varepsilon (j)$ 时的精确度. $1\{ bool\} $ 在 $bool$ 等于true时为1, $bool$ 等于false时为0. $\sqrt {{{\left( {x_i^T\!\!- \!\!x_i^G} \right)}^2}\!\! +\!\! {{\left( {y_i^T\!\! -\!\! y_i^G} \right)}^2}}$ 表示第i帧的目标中心位置 $\left( {x_i^T,y_i^T} \right)$ 与其真实位置 $\left( {x_i^G,y_i^G} \right)$ 的欧式距离. $\displaystyle\sum\limits_{i = 1}^{frames} {1\left\{ { \sqrt {{{\left( {x_i^T - x_i^G} \right)}^2} + {{\left( {y_i^T - y_i^G} \right)}^2}} \le \varepsilon (j)} \right\} }$ 表示所有欧式距离小于 $\varepsilon (j)$ 的帧数, $frames$ 表示某视频序列的帧数.

(2)成功率

成功率求解如下:

$suc(j){\rm{ = }}\frac{{\displaystyle\sum\limits_{i = 1}^{frames} {1\left\{ {\xi (j) \le P\left( {A_i^T \cap A_i^G)/P(A_i^T \cup A_i^G} \right)} \right\}} }}{{frames}}$

(20)

式中, $suc(j)$ 是阈值取 $\xi (j)$ 时的精确度, $1\{ bool\} $ 在 $bool$ 等于true时为1, $bool$ 等于false时为0, $A_i^T$ 表示第i帧的目标框, $A_i^G$ 表示第i帧的真实目标框, $ \cap $ 表示交集, $ \cup $ 表示并集, $P(B)$ 为B框内的像素个数, $\displaystyle\sum\limits_{i = 1}^{frames} 1\left\{ {\xi (j) \le P\left( {A_i^T \cap A_i^G} \right)} \right./$ $\left. {P\left( {A_i^T \cup A_i^G} \right)} \right\}$ 表示像素比大于 $\varepsilon (j)$ 的帧数, $frames$ 表示某视频序列的帧数.

3.3 实验环境及参数设置

实验电脑的处理器是Intel(R) Core(TM) i7-7500U CPU(2.9 GHZ), 内存是8 GB, 开发软件为Matlab R2014b. 算法参数设置如下: 高斯核的方差 $\delta $ 为0.5, Hog特征的细胞单元大小为4×4, Hog特征的方向为9, Hog特征31通道, gray特征1通道, 颜色特征10通道, 模型的学习率 $lr$ 为0.01, 第k通道的初始值 $ratio_0^k{\rm{ = 1}}$ , 通道的权重学习率 $rati{o^{{w}}}{\rm{ = 0}}{\rm{.22}}$ .

3.4 实验结果分析

(1)定量分析

为了定量评估本文算法(WSAMF)的有效性, 我们对比了WSAMF、SAMF、KCF、CN在OTB-2015^[18]数据集的100组视频序列的表现. 我们做了两组实验, 第一组实验取距离阈值 ${\rm{0}} \le \varepsilon (j) \le {\rm{50}}$ 像素、重叠率阈值 ${\rm{0}} \le \xi (j) \le {\rm{1}}$ , 第二组实验取距离阈值 ${\rm{0}} \le \varepsilon (j) \le {\rm{15}}$ 像素、重叠率阈值 ${\rm{0}}{\rm{.5}} \le \xi (j) \le {\rm{1}}$ .

第一组实验用于评估算法的综合性能, 第二组实验用于测试算法的有效性. 因为在实际的目标跟踪过程中, 目标中心位置与实际中心位置的距离超过15像素, 算法基本跟踪失败; 目标框与真实框的重叠率小于0.5时候, 算法基本无效; 所以, 我们在第一组实验的基础上, 做了第二组实验.

第一组实验: 距离阈值 ${\rm{0}} \le \varepsilon (j) \le {\rm{50}}$ 像素、重叠率阈值 ${\rm{0}} \le \xi (j) \le {\rm{1}}$ . 结果如图1所示.

图1(a)为算法执行一次的精度图, 该图显示算法随着距离阈值 $\varepsilon (j)$ 从0像素到50像素的精确度变化. 图1(b)为算法执行一次的成功率图, 该图显示算法随着重叠率阈值 $\xi (j)$ 从0到1的成功率变化. 通过图1可以看出, 相比SAMF、KCF、CN, WSAMF在精确度上分别提升0.78%、8.5%、27.3%, 成功率则分别提升1.3%、21.5%, 42.9%.

为了综合评估本文算法(WSAMF)的性能, 在公开数据集OTB-2015的100个视频序列上, 取距离阈值 ${\rm{0}} \le \varepsilon (j) \le {\rm{50}}$ 像素、重叠率阈值 ${\rm{0}} \le \xi (j) \le {\rm{1}}$ , 对比WSAMF、SAMF、KCF、CN在不同属性下精确度和成功率, WSAMF都取得相对不错的跟踪效果, 具体结果见表1、表2.

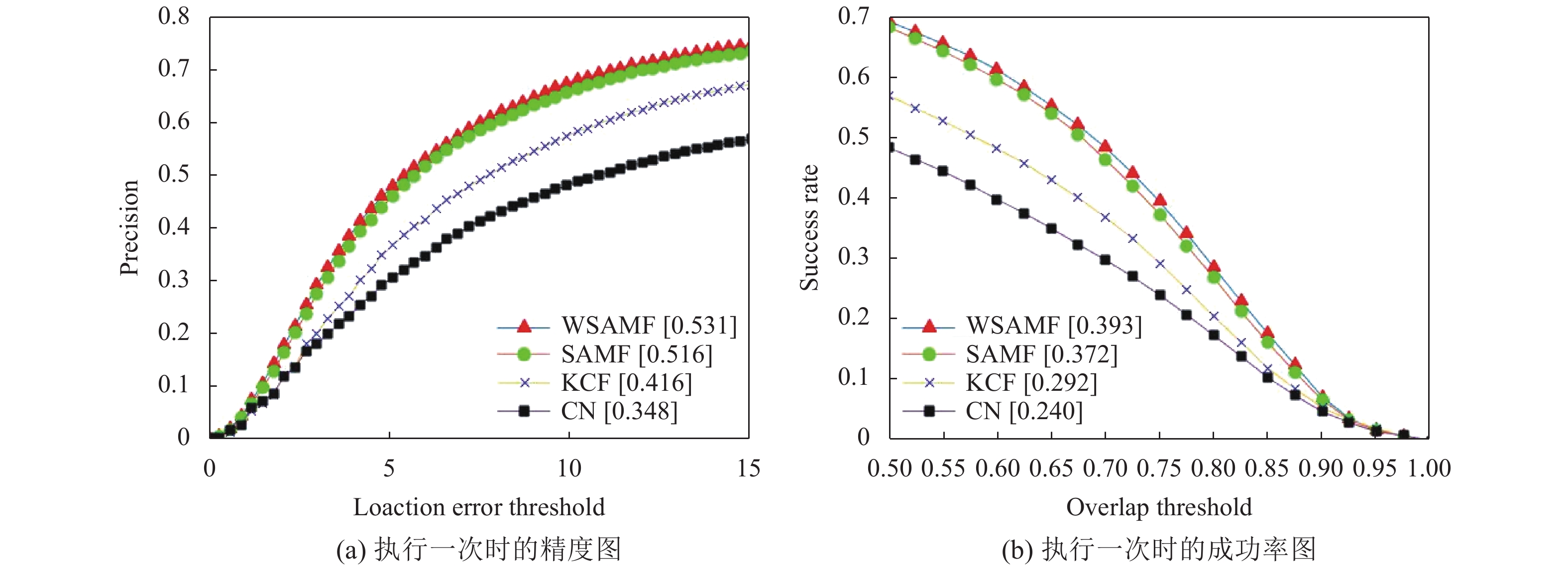
第二组实验: 距离阈值 ${\rm{0}} \le \varepsilon (j) \le {\rm{15}}$ 像素、重叠率阈值 ${\rm{0}}{\rm{.5}} \le \xi (j) \le {\rm{1}}$ . 结果如图2所示.

图2(a)为算法执行一次的精度图, 该图显示算法随着距离阈值 $\varepsilon (j)$ 从0像素到15像素的精确度变化. 图2(b)为算法执行一次的成功率图, 该图显示算法随着重叠率阈值 $\xi (j)$ 从0.5到1的成功率变化. 通过图2可见, 相比SAMF、KCF、CN, WSAMF在精确度上分别提升2.9%, 27.6%, 52.6%, 成功率则分别提升5.6%, 34.6%, 63.8%.

为了测试本文算法(WSAMF)的有效性, 在公开数据集OTB-2015的100个视频序列上, 取距离阈值 ${\rm{0}} \le \varepsilon (j) \le {\rm{15}}$ 像素、重叠率阈值 ${\rm{0}}{\rm{.5}} \le \xi (j) \le {\rm{1}}$ , 对比WSAMF、SAMF、KCF、CN在不同属性下精确度和成功率, WSAMF都取得不错的跟踪效果, 具体结果见表3、表4.

通过以上两组实验可以看出, 本文算法在综合性能、有效性上, 都有一定提升.

(2)定性分析

为了更加直观的评估算法性能, 我们对KCF、CN、SAMF和WSAMF在basketball(DEF)、Jogging-2(OCC)、Car4(IV)、Singer1(IV)、boy(OPR)、doll(SV)和Walking2(SV、OCC)等7个视频序列上进行了定性分析. 为了区分4种算法, 我们选用不同的颜色跟踪框表示. 其中, 红色实线为KCF算法, 绿色虚横线框为CN算法, 蓝色点横线框为SAMF算法, 黑色虚点线框为WSAMF算法.

图3中, 目标在跟踪过程中发生了形变, KCF、CN在第259帧和第266帧只定位目标局部, SAMF在第271帧和第547帧则包含了相对多一点的背景信息, 只有WSAMF能够更好的跟踪这些目标.

图4中, 目标在跟踪过程中发生了遮挡, KCF、CN在第59帧、第60帧、第61帧和第64帧发生漂移, SAMF则包含了相对多一点的背景信息, 只有WSAMF能够更好的跟踪这些目标.

图5中, 目标在跟踪过程中光照变暗, KCF、CN、SAMF在第202帧、第203帧、第218帧和第220帧包含了相对多一点的背景信息, 只有WSAMF能够更好的跟踪这些目标.

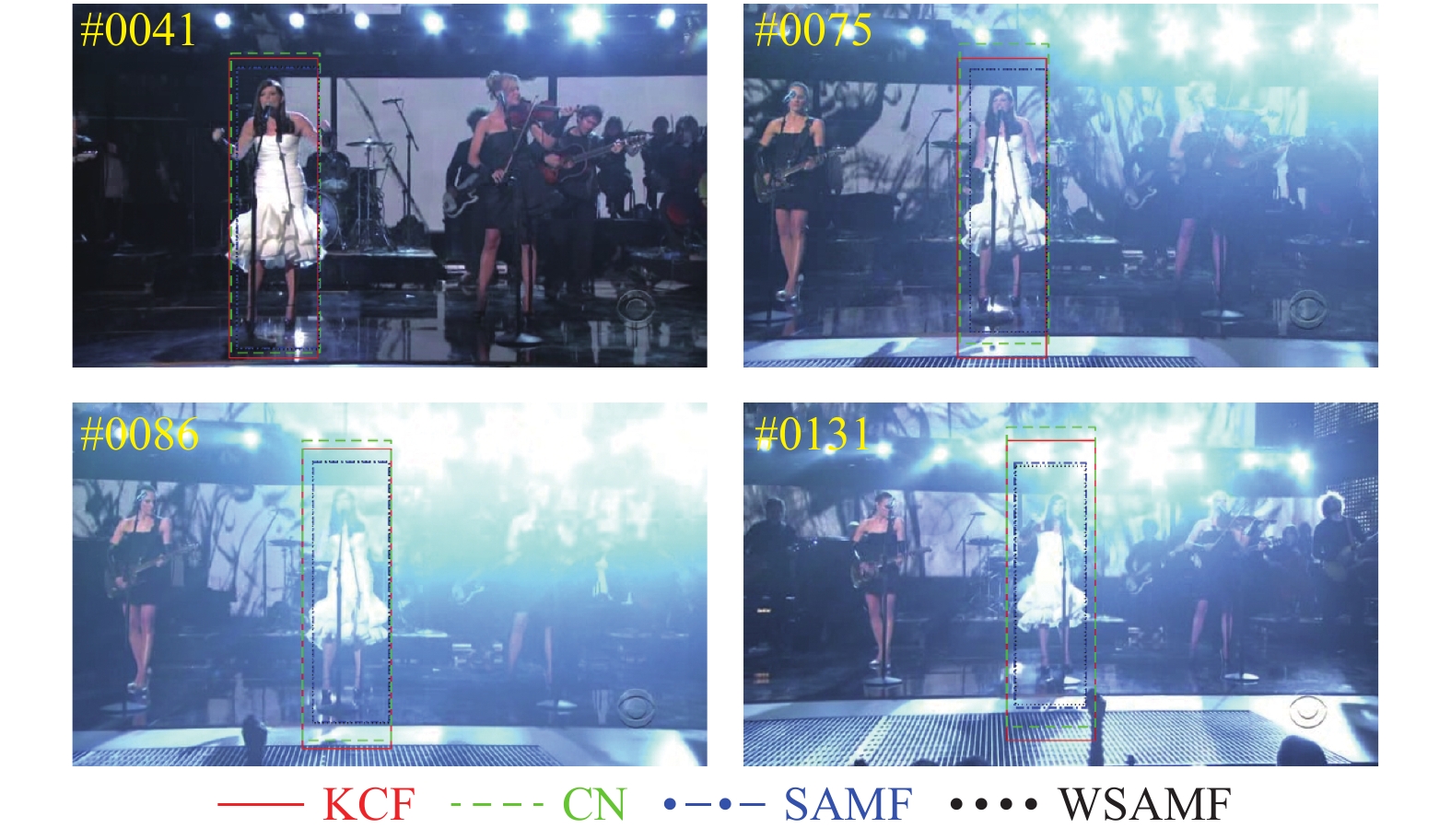
图6中, 目标在跟踪过程中光照增强, KCF、CN在第41帧、第75帧、第86帧和第131帧包含了相对多一点的背景信息, SAMF在第131帧包含了相对多一点的背景信息, 只有WSAMF能够更好地跟踪这些目标.

图7中, 目标在跟踪过程中发生球面外旋转, KCF和CN在第459帧、第462帧、第584帧和第596帧只跟踪到目标的一部分, 而SAMF则跟踪到多一点的背景信息, 只有WSAMF能够更好的跟踪这些目标.

图8中, 目标在跟踪过程中发生尺度变化, KCF、CN在第3526帧、第3669帧、第3721帧和第3737帧发生不同程度的漂移, SAMF跟踪到少一点的目标信息, 只有WSAMF能够更好的跟踪这些目标.

图9中, 目标在跟踪过程中发生遮挡、尺度变化, KCF、CN在第375帧、第487帧和第489帧发生不同程度的漂移, SAMF在第206帧、487帧和489帧跟踪到多一点的背景信息, 只有WSAMF能够更好的跟踪这些目标.

(3)跟踪速度

为了直观的展示跟踪速度, 在OTB-2015数据集上任意选取basketball、Jogging-2、Car4、Singer1、boy、doll和Walking2等7个视频序列上, 对跟踪情况进行对比, 具体情况见表5.

单从表中数据来看, 4种算法都达不到实时要求, 这主要是受电脑硬件条件限制. 在硬件条件获得一定提升后, WSAMF应该可以满足实时性跟踪要求.

另外, 需要补充说明的是, 同一种算法在不同数据集下跟踪速度有一定差异, 这主要是因为不同数据集的跟踪目标、搜索区域数据复杂度不同, 导致计算量不同, 进而导致跟踪速度有差异.

4 结语

本文算法根据各通道对响应值的贡献度调整权重, 构建实时特征组合, 进而控制特征融合. 与现有的基于类别融合特征的算法不同, 该算法从通道层面融合特征. 实验表明该算法能够有效提升目标跟踪的精确度、成功率, 整体性能优于对比算法. 实验中发现, 在目标趋近于完全遮挡的过程过慢时, 由于算法未对目标中背景剔除, 则容易出现不同程度的跟踪漂移甚至失败. 因此, 如何剔除目标中的背景信息或有效区分目标、背景, 将是下一步研究的工作重点.