2. 浪潮集团有限公司 高效能服务器和存储技术国家重点实验室, 北京 100085;
3. 广东浪潮大数据研究有限公司, 广州 510632
2. State Key Laboratory of High-End Server & Storage Technology, Inspur Group Co. Ltd., Beijing 100085, China;
3. Guangdong Inspur Big Data Research Co. Ltd., Guangzhou 510632, China
近年来, 强化学习(Reinforcement Learning, RL)因其强大的探索能力和自主学习能力, 已经与监督学习(supervised learning)、无监督学习(unsupervised learning)并称为三大机器学习技术[1]. 伴随着深度学习的蓬勃发展, 功能强大的深度强化学习算法层出不穷, 已经广泛应用于游戏对抗[2-4]、机器人控制[5,6]、城市交通[7-9]和商业活动[10-12]等领域, 并取得了令人瞩目的成绩. AlphaGo[2]之父David Silver曾指出, “深度学习+强化学习=通用人工智能(artificial general intelligence)”[13], 后续大量的研究成果也表明, 强化学习是实现通用人工智能的关键步骤.
1.1 马尔可夫决策过程(MDP)强化学习的核心是研究智能体(agent)与环境(enironment)的相互作用, 通过不断学习最优策略, 作出序列决策并获得最大回报[14]. 强化学习过程可以描述为如图1所示的马尔可夫决策过程(Markov Decision Process, MDP), 其中参数空间可表示为一个五元组
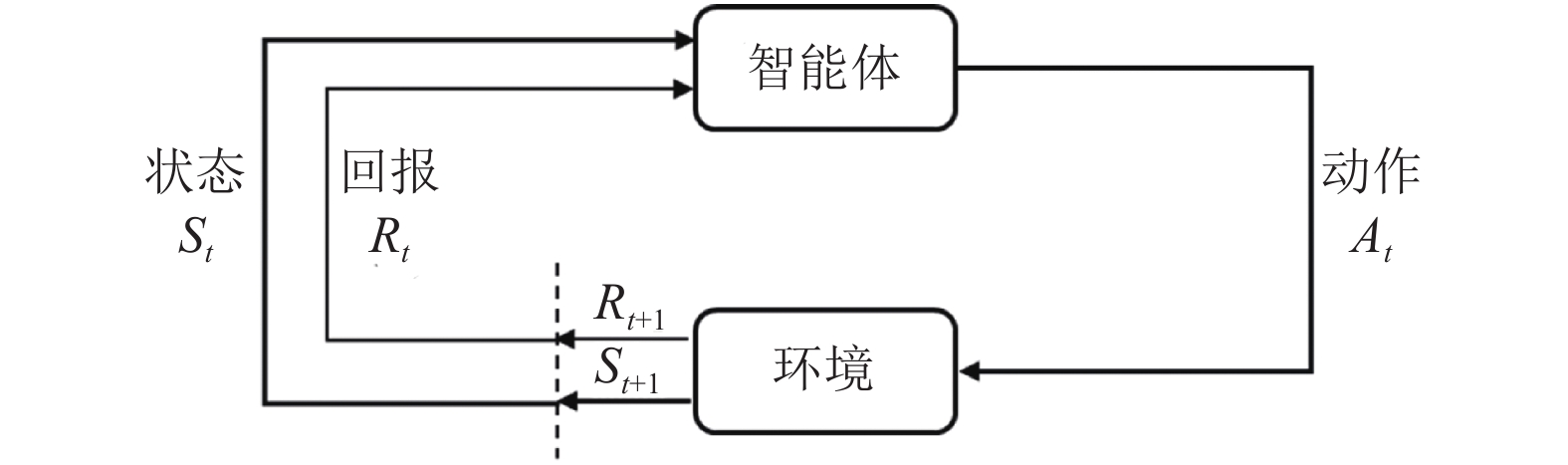
|
图 1 MDP中智能体与环境的交互作用[14] |
具体实施过程中, 智能体在时刻t观测到所处环境和自身当前的状态
| ${s_0},{a_0},{r_1},{s_1},{a_1},{r_2},{s_2},{a_2},{r_3},\cdots,{s_{n - 1}},{a_{n - 1}},{r_n}$ | (1) |
智能体通过不断学习, 找到能够带来最大长期累积回报的最优策略
| ${R_t} = {r_{t + 1}} + \gamma {r_{t + 2}} + \cdots = \sum\limits_{k = 0}^\infty {{\gamma ^k}{r_{t + k + 1}}} $ | (2) |
考虑智能体所处环境的随机性, 以及回报获取存在延迟, MDP使用折扣因子反映越是深入未来的回报, 对当前t时刻累积回报的贡献越小[14].
1.2 价值函数当智能体学习到最优策略
| ${V^{{\pi ^ * }}}(s) = {\rm E}\left[ {{R_t}|{s_t} = s} \right]$ | (3) |
| ${Q^{{\pi ^ * }}}(s,a) = {\rm E}\left[ {{R_t}|{s_t} = s,{a_t} = a} \right]$ | (4) |
将上式转换为贝尔曼最优方程(Bellman optimality equations)形式即为:
| ${V^{{\pi ^ * }}}(s) = \mathop {\max }\limits_a \sum\limits_{s',r} {P\left( {s',r|s,a} \right)\left[ {r + \gamma {V^{{\pi ^ * }}}(s')} \right]} $ | (5) |
| ${Q^{{\pi ^ * }}}(s,a) = \sum\limits_{s',r} {P\left( {s',r|s,a} \right)\left[ {r + \gamma \mathop {\max }\limits_{a'} {Q^{{\pi ^ * }}}(s',a')} \right]} $ | (6) |
获得状态价值函数和动作价值函数后, 理论上可以通过策略迭代的方式获得最优策略, 进而求解价值函数. 但在具体的实践过程中, 策略迭代效率低、计算成本高, 因此通常采用人工设计的线性函数, 或非线性函数(如神经网络)来近似估计价值函数[16].
1.3 探索与利用在强化学习问题中, 智能体需要平衡探索(exploration)与利用(exploitation)的关系来获得最优策略, 进而得到最大累积回报[17]. 采取随机动作来充分探索全部不确定的策略, 可能经历大量较差策略, 导致回报较低; 然而, 持续利用现有最优策略来选取价值最高的动作, 缺乏对状态空间的探索, 可能导致错过全局最优策略, 且回报不稳定.
针对强化学习中的探索与利用问题, 多采用简单的贪婪探索, 即
针对国内外强化学习的研究历程和发展现状, 本文第2章和第3章集中阐述经典强化学习算法与前沿研究方向, 第4章介绍强化学习的应用情况, 第5章给出结论与展望.
2 强化学习经典算法从Bellman提出动态规划方法[19]到AlphaGo打败人类围棋冠军[2],强化学习经历60年的发展, 成为机器学习领域最热门的研究和应用方向. 2006年, 深度学习[20]的提出, 引领了机器学习的第二次浪潮, 在学术界和企业界持续升温, 并成功促进了2010年之后深度强化学习的蓬勃发展.
强化学习算法有众多分类方式, 如根据是否构建模型可以分为无模型(model-free)算法和基于模型(model-based)算法; 依据执行策略与评估策略是否一致, 分为同步策略(on-policy)算法和异步策略(off-policy)算法; 根据算法更新机制, 分为回合更新的蒙特卡洛(Monte-Carlo, MC)算法和单步更新的时间差分(Temporal-Difference, TD)算法. 其中, 无模型(model-free)算法、同步策略(on-policy)算法、时间差分算法(TD)算法, 是各自分类下的主流方向, 不同分类下的算法存在一定交叉. 另外, 依据智能体动作选取方式, 可将强化学习算法分为基于价值(value-based)、基于策略(policy-based), 以及结合价值与策略(actor-critic) 3类, 这也是目前最主流的分类方式[21]. 表1中给出3类主流强化学习算法的对照, 下文将对每一类算法展开介绍.
| 表 1 3类主流强化学习算法对照 |
2.1 基于价值(value-based)的强化学习算法
基于价值(value-based)的强化学习算法通过获取最优价值函数, 选取最大价值函数对应的动作, 隐式地构建最优策略. 代表性算法包括Q-learning[22]、SARSA[23], 以及与深度学习相结合的Deep Q-Network (DQN)算法[24,25]. 此类方法多通过动态规划(dynamic programming)或值函数估计(value function approximation)的方法获得最优价值函数, 且为确保效率采用时间差分(TD)方法进行单步或者多步更新, 而不是蒙特卡洛(MC)回合更新方式. 例如, 异步策略(off-policy)的Q-learning算法使用非探索策略计算时间差分误差(TD error), 而同步策略(on-policy)的SARSA算法使用探索策略计算时间差分误差(TD error). Value-based算法的样本利用率高、价值函数估值方差小, 不易陷入局部最优. 但是, 此类算法只能解决离散动作空间问题, 容易出现过拟合, 且可处理问题的复杂度受限. 同时, 由于动作选取对价值函数的变化十分敏感, value-based算法收敛性质较差.
DQN算法[24]中使用卷积神经网络(Convolutional Neural Network, CNN)估计价值函数, 是第一个深度强化学习算法, 将value-based方法的应用范围拓展到高维度问题和连续空间问题. DQN这种端到端(end-to-end)的强化学习算法中使用经验重放(experience replay)和目标网络(target network)稳定了价值函数估计, 显著降低对特定领域知识的要求, 并提高了算法的泛化能力. 此后, DQN算法演化出众多变体, 如使用不同网络评估策略和估计价值函数的Double DQN算法[26], 差异化不同经验重放频率的优先经验重放(prioritized experience replay)算法[27], 采用竞争网络结构分别估计状态价值函数和相关优势函数、再结合两者共同估计动作价值函数的Dueling DQN算法[28], 添加网络参数噪声以提升探索度的NoisyNet算法[29], 拓展到分布式价值函数的Distributional DQN (C51)算法[30], 以及综合以上各种算法的Rainbow DQN[30]. 这些DQN算法能够有效解决过拟合的问题, 具备更高的学习效率、价值函数评估效果和更充分的空间搜索能力, 以及更广泛的适用性. 图2中展示了DQN算法及各类变种算法的性能对比.

|
图 2 各类DQN算法在Atari游戏(57种)中的表现[31] |
需要指出的是, DQN及其各变体算法(后文简称DQN算法)虽然在以电子游戏为代表的离散动作空间问题上取得了优异的表现, 甚至在一些游戏上以压倒性优势战胜人类玩家[25], 但针对实际生产、生活中大量存在的连续动作空间问题, 如机械手臂控制、车辆驾驶等, 面向离散动作空间的DQN算法无法应对. 同时, 相比SARSA等同步策略算法, 虽然异步策略的DQN算法已经具有较高的样本效率, 但正如图2所示, 即使DQN系列中最先进的Rainbow DQN算法, 在面对简单的Atari游戏时, 仍然需要学习约1500万帧图像(样本)、持续训练1天时间才能达到人类玩家的水平[31], 而人类只需几个小时就能掌握同一游戏. 因此, DQN算法的采样效率问题仍然不可忽视.
2.2 基于策略(policy-based)的强化学习算法基于策略(policy-based)的强化学习算法跨越价值函数, 直接搜索最佳策略. Policy-based算法通过最大化累积回报来更新策略参数, 分为基于梯度(gradient-based)算法和无梯度(gradient-free)算法[41]. 无梯度算法[42,43]能够较好地处理低维度问题, 基于策略梯度算法仍然是目前应用最多的一类强化学习算法, 尤其是在处理复杂问题时效果更佳, 如AlphaGo[2]在围棋游戏中的惊人表现. 相比value-based算法, policy-based算法能够处理离散/连续空间问题, 并且具有更好的收敛性. 与此同时, policy-based方法轨迹方差较大、样本利用率低, 容易陷入局部最优的困境.
经典的策略梯度算法REINFORCE[32]使用蒙特卡洛(MC)方法估计梯度策略, 具有较好的稳定性. 但样本效率较低, 同时MC方法包含整个轨迹上的信息, 会带来较大的策略梯度估计方差. 通过引入少量噪声的无偏估计, 例如在回报中减去基线的方式, 能够有效降低估计方差. Kakade在2002年提出自然策略梯度(natural policy gradient)[44]来提升算法的稳定性和收敛速度, 由此引出了后续的置信域(trust region)方法, 例如著名的置信域策略优化算法TRPO (Trust Region Policy Optimization)[33]和近端策略优化算法PPO (Proximal Policy Optimization)[34]. TRPO和PPO均为同步策略(on-policy)算法, 在经典策略梯度算法的基础上通过人为或自适应的方式选择超参数, 将更新步长约束一定范围内, 以确保每一步回报单调不减, 持续获得更优的策略, 防止出现策略崩溃(Policy Collapse)的问题. 此外, Nachum等在2017年提出了样本效率更高的异步策略(off-policy)置信路径一致性学习算法Trust_PCL (Trust Path Consistency Learning)[15], 同年Heess等将PPO算法推广到分布式策略梯度的Distributed PPO算法[45].
TRPO和PPO算法因其良好的实验效果, 被选为许多研究工作的基础算法[46-49], PPO更是成为了OpenAI的默认算法[1]. 然而, 尽管TRPO和PPO算法具有十分优秀的超参数性能, 在学术研究中获得了广泛关注, 但是作为典型的同步策略算法, 每次策略更新时都需要在当前策略下采样大量样本进行训练和确保算法收敛. 因此, TRPO和PPO算法的局限性也非常明显, 算法采样效率低, 需要大量算力作为支撑, 这些都极大限制了算法在应用领域的推广.
2.3 执行者-评论者(actor-critic)强化学习算法执行者-评论者(actor-critic)算法将value-based (对应评论者, critic)方法与policy-based (对应执行者, actor)方法进行结合, 同时学习策略和价值函数[35]. Actor根据critic反馈的价值函数训练策略, 而critic训练价值函数, 使用时间差分法(TD)进行单步更新. Actor-critic算法的框架如图3所示. 通常情况下, actor-critic被认为是一类policy-based方法, 特殊之处在于使用价值作为策略梯度的基准, 是policy-based方法对估计方差的改进. Actor-critic兼备policy-based方法和value-based方法两方面的优势, 值函数估计方差小、样本利用率高, 算法整体的训练速度快. 与此同时, actor-critic方法也继承了相应缺点, 例如actor (policy-based)对样本的探索不足, critic (value-based)容易陷入过拟合的困境. 并且, 本身不易收敛的critic在与actor结合后, 收敛性质更差. 后续发展的算法中, 通过引入深度学习等手段, 在一定程度上缓解了这些问题.
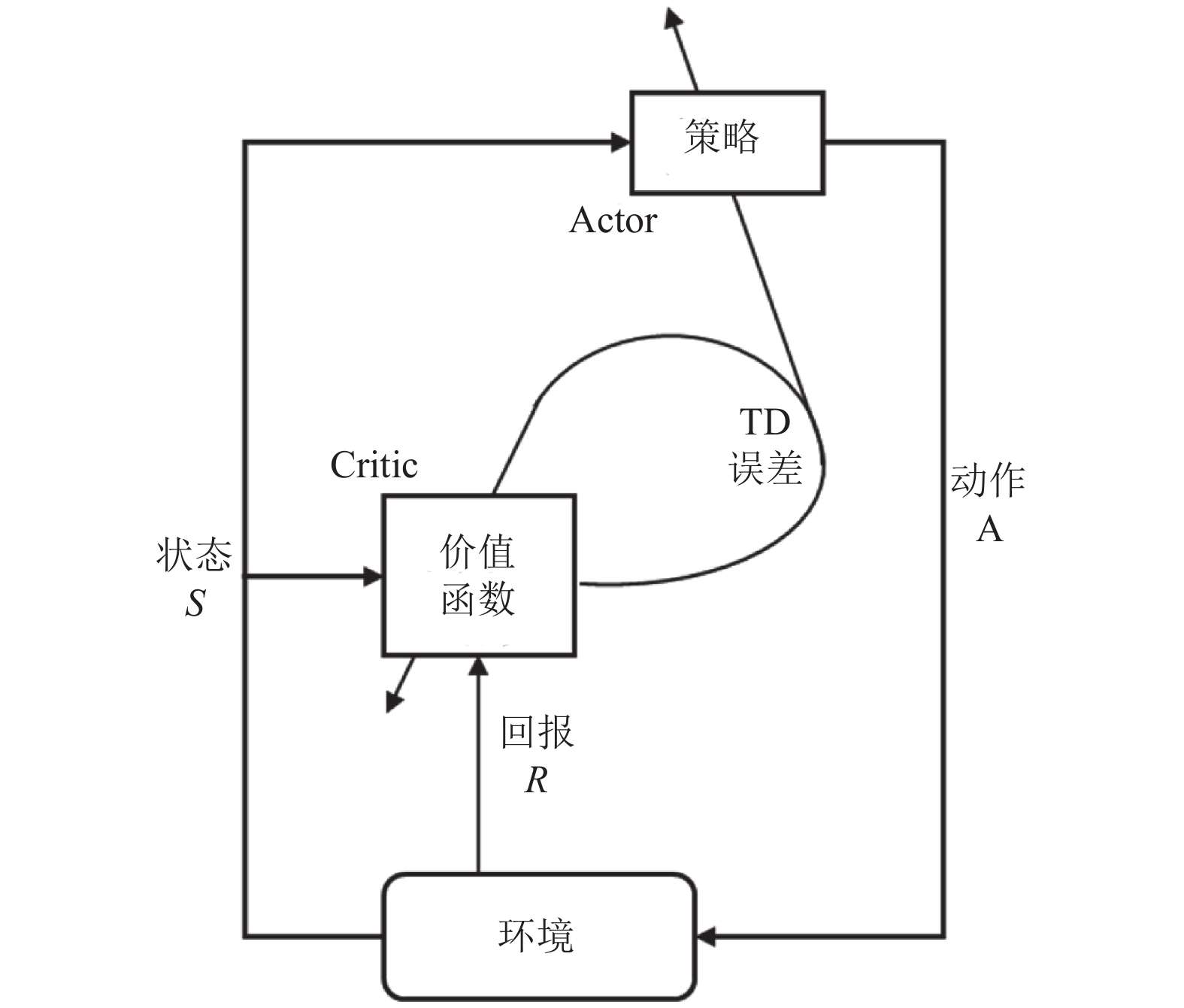
|
图 3 Actor-critic算法框架 |
近年来, 发展出众多改进的actor-critic算法, 最具代表性的算法包括: 确定性策略梯度算法DPG (Deterministic Policy Gradient)[37]及其深度改进版本DDPG (Deep Deterministic Policy Gradient)[38]、异步优势actor-critic算法A3C (Asynchronous Advantage Actor-Critic)[36]、双延迟确定性策略梯度算法TD3 (Twin Delayed Deep Deterministic policy gradient)[39], 以及松弛actor-critic算法SAC (Soft Actor-Critic)[40]等. DPG算法[37]仅在状态空间整合确定性策略梯度, 极大降低了采样需求, 能够处理较大动作空间的问题. DDPG算法[38]继承了DQN的目标网络, 采用异步策略的Critic估计策略梯度, 使训练更加稳定简单. 著名的A3C算法[36]使用在线Critic整合策略梯度, 降低训练样本的相关性, 在保证稳定性和无偏估计的前提下, 提升了采样效率和训练速度. TD3算法[39]在DDPG的基础上, 引入性能更好的Double DQN, 取两个Critic之间的最小值来限制过拟合. 与TD3同期的SAC算法[40]中, Actor在获得最大回报之外, 也具有最大熵, 大大提升算法的探索能力. 图4中对比了几种最先进的policy-gradient算法在同一个强化学习基准问题上的表现, 整体对比效果约为SAC=TD3>DDPG=TRPO=DPG>VPG[50]. 其中, VPG指经典的策略梯度算法, 如REINFORCE[32].

|
图 4 基于策略的强化学习算法(含actor-critic)在Hopper问题的效果对比[50] |
Actor-critic的代表性算法, 如DPG、DDPG、TD3及SAC算法, 其中critic采用了异步策略的Q-learning、DQN算法, 都是典型的异步策略算法, 而A3C可根据critic所采用的算法进行同步/异步训练, 能适用于同步策略、异步策略. 因此, actor-critic算法多是异步策略算法, 能够通过经验重放(experience replay)解决采样效率的问题. 然而, 策略更新与价值评估相互耦合, 导致算法的稳定性不足, 尤其对超参数极其敏感. Actor-critic算法的调参难度很大, 算法也难于复现, 当推广至应用领域时, 算法的鲁棒性也是最受关注的核心问题之一.
3 强化学习前沿研究近年来, 在传统强化学习算法的基础上, 结合多智能体系统理论、元学习、迁移学习等研究手段, 延伸出众多前沿研究方向, 如面向更现实场景的多智能体强化学习(Multi-Agent RL, MARL)、借助元学习泛化能力的元强化学习(Meta RL)、致力于解决大规模问题维度爆炸的分层强化学习(Hierarchical RL), 以及迁移先验知识的强化学习等. 本节选取关注度最高、研究最广泛的多智能体强化学习和元强化学习方向, 介绍其中核心思想和代表性算法.
3.1 多智能体强化学习复杂的现实场景中往往包含多个智能体协作、通信和对抗, 例如生产机器人、城市交通信号灯、电商平台搜索平台等, 都是典型的多智能体系统. 目前, 应用于多智能体系统的强化学习正在逐渐发展成为研究和应用热点[51]. 除了传统强化学习中的稀疏回报和采样效率问题, 多智能体强化学习还面临着更多的挑战, 例如多智能体如何达到纳什均衡[52], 每个智能体如何应对其他智能体造成的非平稳环境, 如何仅凭自身观测到的部分信息做出决策和更新策略[53], 如何实现各个智能体之间的通信[54], 以及在多智能体系统中十分重要的信用分配(credit assignment)问题[51]. 此外, 当智能体数量增多时, 维度爆炸的问题也愈发突出[1].
根据任务的类型, 多智能体强化学习(Multi-Agent RL, MARL)可分为完全合作、完全竞争和混合模式. MARL的关键是学习联合动作价值函数和优秀的分布式策略, 实现系统均衡和回报最优[55]. 早期的MARL算法, 如针对两个智能体零和博弈的MiniMax-Q learning[56]、扩展到多个智能体一般和博弈的Nash-Q learning[57], 以及将一般和博弈转化为两个零和博弈的FFQ (Friend-or-Foe Q-learning)算法[58], 需要使用巨大空间来存储Q值, 同时线性规划也导致算法整体学习速度较慢, 因此多适用于小规模的问题. 此外, Tan在1993年提出IQL (Independent Q-Learning)算法[59], 按照传统强化学习的步骤对每一个智能体分别执行Q-learning. 由于多智能体问题的环境是动态不稳定的, IQL算法无法收敛, 但仍在部分应用中取得良好的效果.
近几年, 以actor-critic架构为基础的MARL算法成为重要发展方向之一. 代表性算法有MADDPG(Multi-Agent Deep Deterministic Policy Gradient)[60]和COMA (COunterfactual Multi-Agent actor-critic)[61]. 此类算法采用集中式训练、分布式执行(centralized training for decentralized execution), 利用联合动作的所有状态信息训练出一个集中的critic, 每个智能体通过自身观测到的历史信息学习策略, 都有自己的回报函数, 并分别执行各自的actor, 能够较好地处理非平衡问题, 可应用于合作任务、对抗任务和混合任务. 然而, 这种中心化算法中critic使用全局信息, 当智能体数目增多时, 算法的可扩展性较差, 集中的critic更难训练, 多智能体信用分配问题更难解决. 同时, 一旦环境中某个智能体学习到较好的策略, 其他智能体将会变得懒惰, 进而影响整体进度.
不同于actor-critic类型的方法中, 每一个智能体都有各自独立的回报函数, 在基于价值分解(value-decomposition)的MARL算法中, 多个智能体通过各自的观测得到局部价值函数, 再合并为联合动作价值函数, 代表性算法有简单加和局部价值函数的VDN(Value-Decomposition Network)[62], 以及采用非线性混合网络(mix network)来联合价值函数的QMIX[63]. 因此, 基于价值函数分解的方法只能应用于合作问题, 在此过程中理解智能体之间的关系尤为关键. 此外, Yang等提出的平均场方法MFMARL (Mean Field Multi-Agent Reinforcement Learning)[64], 将一个智能体与其邻居智能体间的相互作用简化为两个智能体间的关系, 即智能体与其邻居智能体均值的相互作用, 极大减缓了智能体数量增加带来的维数爆炸问题. 平均场方法只能将智能体的动作空间进行维度缩减, 而每个智能体进行策略更新时仍然需要获取全局状态信息.
3.2 元强化学习(Meta RL)尽管强化学习具有很好的研究和应用前景, 但从头开始训练算法时, 获取样本的代价过于高昂, 严重阻碍强化学习研究与应用的发展. “Learning to learn”的元学习(meta-learning)为快速、灵活的强化学习提供了可能[65]. 在元强化学习(meta RL)体系当中, 通过在大量先验任务(prior tasks)上训练出泛化能力强的智能体(agent)/元学习者(meta-learner), 在面对新任务时只需少量样本或训练步即可实现快速适应.
早期的元强化学习研究中多使用循环神经网络(Recurrent Neural Network, RNN)表示智能体[46,66]. 之后, 加州大学伯克利分校的人工智能研究组BAIR(Berkeley Artificial Intelligence Research)提出了著名的模型无关元学习方法(Model-Agnostic Meta-Learning, MAML)[53], 通过“二重梯度”算法找到泛化能力最强的参数, 只需一步或几步梯度下降实现对新任务的快速适应. MAML不限定具体的网络模型, 通过改变Loss函数去解决各类问题, 如回归、分类和强化学习. 之后众多工作以此为基础发展出性能更优的算法, 如增加结构化噪声扩大搜索范围的MAESN (Model-Agnostic Exploration with Structured Noise)算法[48], 识别模型任务分布、调整参数的多模型MMAML (Multimodel Model-Agnostic Meta-Learning)算法[67]. 同时, MAML算法因其良好的泛化性能, 已被推广到自适应控制[68]、模仿学习[69-71]、逆强化学习[72]和小样本目标推理[73]等研究领域. 然而, 以MAML为基础的一系列算法中, “二重梯度”过程极大增加了计算量, 同时外层循环采用TRPO、PPO等同步策略方法, 算法在元训练阶段的采样效率较低.
除了以上同步策略算法之外, Rakelly等提出了一种异步策略的、概率表示的强化学习算法PEARL[74](Probabilistic Embeddings for Actor-critic RL), 极大提高了样本效率, 并采用后验采样提高探索效率, 相比同步策略算法实现了20–100倍的元训练(meta-training)采样效率提升, 以及显著的渐进性能提升. 同时, 由于概率表示量的引入, PEARL算法具有更强的探索能力, 能够很好地解决稀疏回报问题. 需要指出的是, PEARL算法并不针对一个新任务去更新策略参数, 而是利用概率表示的潜在上下文信息泛化到新任务. 一旦新任务与元训练任务间存在较大差异, PEARL算法的表现将大幅下降. 此外, Mendonca等在最近的工作中提出一种新的引导式元策略学习方法GMPS (Guided Meta-Policy Search)[49], 通过多个异步策略的局部学习者(local learner)独立学习不同的任务, 再合并为一个中心学习者(centralized learner)来快速适应新的任务, 同样实现了元训练效率跨量级的提升. 此外, GMPS算法能够充分利用人类示范或视频示范, 适应稀疏回报的操纵性问题. 虽然GMPS算法在采样效率、探索效率、稀疏回报问题上均有十分优异的表现, 但其中的元(训练)策略非常复杂, 进一步增加了异步策略超参数的敏感性, 算法的复现和应用难度极大.
4 强化学习应用从提出至今的60多年里, 强化学习已经在科学、工程和艺术等领域获得了越来越广泛的应用, 并产生了众多成功案例[1]. 本节选取强化学习应用较多的游戏对抗、机器人控制、城市交通和商业等领域, 针对近年来的应用进展作简要介绍.
4.1 强化学习在游戏对抗领域的应用游戏作为人工智能算法绝佳的实验床, 从中诞生了众多代表性算法. 在之前的众多电子游戏中, 强化学习算法取得了不错的成绩, 在一些游戏中甚至超过了人类玩家, 例如DQN及其各类变种在Atari 2600游戏中表现优异[24,31]. 当然, 最著名的还是Silver等提出的针对零和、信息完备的回合制棋类游戏程序AlphaGo、AlphaGo Zero和Alpha Zero[2,75,76]. “Alpha系列”使用蒙特卡洛树搜索(Monte-Carlo Tree Search, MCTS)[77]的基础架构, 将价值网络(value network)、策略网络(policy network)和快速走子(fast rollout)模块结合起来, 形成一个完整的系统. 强化学习拓展了树搜索的深度和宽度, 平衡探索(exploration)与利用(exploitation)的关系, 通过智能体的自我博弈(self-play)获得了非常显著的效果. “Alpha系列”程序先后战胜了当时的人类世界围棋冠军, 并将这种优势推广到中国象棋与日本将棋.
同时, 强化学习算法也被应用于多人参与游戏, 如在非完备信息、涉及心理学的多人博弈游戏——德州扑克中, 利用反事实后悔最小化(Counter Factual Regret minimization, CFR)[3,78]的递归推理, 处理信息不对称的问题, 实现广义的纳什均衡, 并在六人德州扑克游戏中首次战胜了5名人类顶尖选手. 另外, 地图不完全公开的多人电子游戏中, OpenAI Five在高度复杂、局部观测、玩家高度配合的5v5 Dota2游戏中战胜人类高手[79], Pang等设计的程序也在StarCraft II游戏中表现优异[4].
4.2 强化学习在机器人领域的应用机器人是强化学习最经典也最具发展潜力的应用方向[72], 强化学习核心的MDP序列决策特性为机器人复杂的工程设计提供了可能, 如机械臂运动[69-71,80], 直升机、无人机操控[6,81]、机器人自动导航[82,83]等. 在机器人打乒乓球[80]的应用中, 机器人观测到乒乓球的位置、速度变化, 以及手臂关节的位置和速度等状态信息, 通过不断调整挥臂策略和动作, 直至学会将不同方向飞来的乒乓球击回. 近年来, 基于元强化学习的机器人模仿学习获得了快速发展, 在BAIR基于MAML算法[53]的系列工作中[69-71], 分别让机器人观看人类动作示范和视频示范, 通过在大量元任务上训练, 逐步学会根据示范学会元学习策略. 随后, 机器人面对没有见到过的新任务时, 能够很快完成对物品的抓取、归类等动作. 另外, 已经有一些研究开始探索实际生产线上的人机协作问题[84,85].
在实际的应用过程中, 由于样本获取困难, 智能体状态空间维度高, 以及模型很难抓取动态系统的特征等问题, 还没有实现真正的工业级应用[5].
4.3 强化学习在城市交通领域的应用现代城市交通中, 机动车数量日益增多, 部分道路拥堵严重, 行人与非机动车又具有很高的随机性, 路况十分复杂, 对顺畅交通和参与者的安全带来巨大挑战. 由此, 城市交通网络调配和机动车驾驶纷纷将目光投向人工智能技术领域, 发展城市智慧交通和自动/辅助驾驶技术[86]. 其中, 强化学习算法因其核心的MDP过程与城市交通网络调配的需求高度吻合, 获得了越来越多的关注与应用. 最近的一些工作研究了实际城市交通中交通信号灯的统一调控[7,87,88], 以及城市道路设计问题[89], 研究如何改善真实的城市交通. 同时, 机动车自动/辅助驾驶技术深受各大汽车生产厂商和技术公司的关注[90]. 其中, 辅助/自助驾驶控制系统作为MDP过程中的智能体, 通过观测机动车行驶状态、交通信号灯, 以及周围车辆、行人和非机动车的运动和分布情况, 充分感知周围路况信息. 根据观测到的环境状态, 借由基于价值函数或策略的强化学习方法, 控制系统发出方向盘转向、加速、减速、急停、等待等一系列指令, 辅助人类驾驶员实现智能导航、路线规划, 避让行人、非机动车和紧急避险等操作, 保障各交通参与者的安全和道路畅通[8]. 后续工作中, 研究人员进一步针对城市交通中车辆稠密[91,92]和少数极端路况[93]进行自动驾驶汽车模拟.
随着网约车经济的发展, 越来越多的人选择网约车的方式出行. 为提升服务效果, 强化学习被大量应用于网约车派单业务中. 以滴滴出行AI Lab为代表的企业研究院进行了大量的研究工作和应用实践[9,94,95]. 其中, 乘客与潜在司机之间的距离、道路拥堵程度和司机服务评分等多种因素作为环境状态, 派单系统不断优化策略进行派单, 为乘客匹配最合适的司机, 最小化乘客等待时间, 以及减少司机空车等待时间, 获得最大的收益.
4.4 强化学习在商业领域的应用近年来, 搜索引擎、数字媒体、电子商务逐渐深入到人们的日常生活中, 深刻改变了人们的生活方式. 强化学习作为一种有效的基于用户与系统交互过程建模和最大化累积收益的学习方法, 在信息检索、商品推荐、广告推送等场景中都具有十分广阔的应用潜力和众多成功案例[96].
相关性排序是信息检索应用的关键, 而学会排序(Learning-to-Rank, LTR)又是其中的核心技术[97]. 信息检索系统中, 搜索引擎(agent) 在用户(environment)每次请求时做出相应排序决策(action), 用户根据搜索引擎给出的结果反馈点击、翻页等信号. 据此, 搜索引擎在收到新的请求时会做出新的排序决策. 这个决策过程会持续到用户购买商品或退出搜索为止[10,98]. 推荐系统的核心是根据用户的历史行为, 尽可能准确地推荐最符合用户偏好的商品/信息[99]. 在MDP设定下, 用户的偏好即环境状态, 而转移函数则描述一段时间内用户偏好的动态变化属性. 每次系统向用户推荐商品/信息, 用户给出相应的反馈, 如跳过、点击浏览或购买, 其中体现用户对被推荐商品的满意度. 根据用户的历史行为, 系统调整对用户偏好的判定, 即环境状态发生改变, 并做出下一次推荐[100]. 推荐系统的目标是向用户推荐最相符的商品/信息, 实现用户点击率和逗留时间的最大化[11]. 在线广告的目标是将正确的广告推送给正确的用户, 强化学习在其中为广告发布者提供最大化目标的合作策略[101]和竞价策略[12], 从而使广告活动的收入、点击率(Click Through Rate, CTR)或投资回报率(Rate Of Investment, ROI)最大化.
5 结论与展望强化学习作为一种端到端的学习过程, 以MDP为基础做出序列决策和训练最优策略, 具有很强的通用性, 已经吸引了学术界与企业界的广泛关注, 也被认为是实现通用人工智能的关键步骤. 本文综述了强化学习算法与应用的研究进展和发展动态, 重点介绍基于价值函数、基于策略搜索、结合价值与搜索的代表性强化学习方法, 以及多智能体强化学习和元强化学习等前沿研究的最新进展, 这些算法都促进强化学习向着更加通用化、更加便捷的方向发展. 最后, 本文概述了强化学习在游戏、机器人、城市交通和商业领域的成功应用, 展示了强化学习智能决策特性的优势和潜力.
尽管强化学习在研究和应用领域已经取得了一定的成功, 但本质上仍局限于模拟环境中理想、高度结构化的实验数据, 强化学习还不具备类人的自主学习、推理和决策能力. 为了进一步向通用人工智能的目标迈进, 强化学习研究与应用有以下几个努力方向:
(1)借助监督学习手段, 提高强化学习鲁棒性. 基于策略梯度的强化学习算法是现有研究的主流, 然而不可避免地带有方差大的缺点, 对算法的稳定性造成影响. 对此, 可以结合更高效、更稳定的监督学习方法, 如模仿学习(imitation learning)、行为克隆(behavioral cloning), 充分利用专家经验快速训练出更优的策略.
(2)构建更智能的强化学习表示与问题表述方式. 关注算法的数学本质, 设计具有可解释性、简单的强化学习策略, 摒弃单纯“调参”手段, 从根源上拓展算法的适用性, 降低算法复杂度, 突破强化学习中探索与应用、稀疏回报和样本效率等核心问题.
(3)添加记忆模块, 利用上下文信息增强强化学习的自主学习能力. 在强化学习模型中整合不同类型的记忆模块, 如LSTM、GRU等模型, 引入额外的回报和之前的动作、状态信息, 使得智能体学习到更多任务级别信息, 从而使智能体掌握更多的自主学习、推理和决策等功能.
(4)将元学习、迁移学习拓展到多智能体强化学习研究和应用领域. 针对真实任务场景中普遍存在的多智能体系统, 如生产线机器人、城市道路车辆等, 避免大量智能体从头开始训练的高成本与不确定性, 吸收元学习、迁移学习的思想, 利用先验知识训练出快速适应新任务的模型, 缓解MARL对强大算力支撑的需求, 向复杂场景的应用更进一步.
(5)开发针对实体输入的强化学习算法, 应对实际工业生产应用. 实际生产、生活中, 智能体面对高维环境如实际物品、视频画面等实物信息, 而非原始的像素级信息. 在此过程中, 利用无监督学习或其他机器学习技术对实物、实物间关系进行理解和特征提取, 将大幅提高强化学习算法的效率, 促进强化学习算法在真实场景中的应用.
| [1] |
Li YX. Deep reinforcement learning: An overview. arXiv preprint arXiv: 1701.07274, 2018.
|
| [2] |
Silver D, Huang A, Maddison CJ, et al. Mastering the game of go with deep neural networks and tree search. Nature, 2016, 529(7587): 484-489. DOI:10.1038/nature16961 |
| [3] |
Moravčík M, Schmid M, Burch N, et al. DeepStack: Expert-level artificial intelligence in heads-up no-limit poker. Science, 2017, 356(6337): 508-513. DOI:10.1126/science.aam6960 |
| [4] |
Pang ZJ, Liu RZ, Meng ZY, et al. On reinforcement learning for full-length game of starcraft. arXiv preprint arXiv: 1809.09095v1, 2018.
|
| [5] |
Kober J, Bagnell JA, Peters J. Reinforcement learning in robotics: A survey. The International Journal of Robotics Research, 2013, 32(11): 1238-1274. |
| [6] |
Ng AY, Kim HJ, Jordan MI, et al. Inverted autonomous helicopter flight via reinforcement learning. International Symposium on Experimental Robotics (ISER). Singapore City, Singapore. 2004.
|
| [7] |
Wei H, Zheng GJ, Yao HX, et al. IntelliLight: A reinforcement learning approach for intelligent traffic light control. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York, NY, USA. 2018. 2496–2505.
|
| [8] |
Bojarski M, Testa DD, Dworakowski D, et al. End to end learning for self-driving cars. arXiv preprint arXiv: 1604.07316v1, 2016.
|
| [9] |
Li MN, Qin ZW, Jiao Y, et al. Efficient ridesharing order dispatching with mean field multi-agent reinforcement learning. The World Wide Web Conference. San Francisco, CA, USA. 2019. 983–994.
|
| [10] |
Hu YJ, Da Q, Zeng AX, et al. Reinforcement learning to rank in e-commerce search engine: Formalization, analysis, and application. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York, NY, USA. 2018. 368–377.
|
| [11] |
Zheng GJ, Zhang FZ, Zheng ZH, et al. DRN: A deep reinforcement learning framework for news recommendation. Proceedings of the 2018 World Wide Web Conference. Lyon, France. 2018. 167–176.
|
| [12] |
Cai H, Ren K, Zhang WN, et al. Real-time bidding by reinforcement learning in display advertising. Proceedings of the 10th ACM International Conference on Web Search and Data Mining. 2017. Cambridge, UK. 661–670.
|
| [13] |
Silver D. Deep reinforcement learning, a tutorial at ICML 2016. http://icml.cc/2016/tutorials/deep_rl_tutorial.pdf, 2016.
|
| [14] |
Sutton RS, Barto AG. Reinforcement Learning: An Introduction. 2nd ed. Massachusetts: MIT Press, 2018.
|
| [15] |
Nachum O, Norouzi M, Xu K, et al. Bridging the gap between value and policy based reinforcement learning. Annual Conference on Neural Information. Long Beach, CA, USA. 2017.
|
| [16] |
刘全, 翟建伟, 章宗长, 等. 深度强化学习综述. 计算机学报, 2018, 41(1): 1-27. DOI:10.11897/SP.J.1016.2019.00001 |
| [17] |
Wang HR, Zariphopoulou T, Zhou XY. Exploration versus exploitation in reinforcement learning: A stochastic control approach. arXiv preprint arXiv: 1812.01552, 2018.
|
| [18] |
Auer P. Using confidence bounds for exploitation-exploration trade-offs. The Journal of Machine Learning Research, 2003, 3(3): 397-422. |
| [19] |
Bellman RE. Dynamic Programming. Princeton: Princeton University Press, 1957.
|
| [20] |
Hinton GE, Salakhutdinov RR. Reducing the dimensionality of data with neural networks. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647 |
| [21] |
马骋乾, 谢伟, 孙伟杰. 强化学习研究综述. 指挥控制与仿真, 2018, 40(6): 68-72. DOI:10.3969/j.issn.1673-3819.2018.06.015 |
| [22] |
Watkins CJCH, Dayan P. Q-learning
. Machine Learning, 1992, 8(3–4): 279-292. |
| [23] |
Rummery GA, Niranjan M. On-line Q-learning Using Connectionist Systems. Cambridge: University of Cambridge, 1994.
|
| [24] |
Mnih V, Kavukcuoglu K, Silver D, et al. Playing atari with deep reinforcement learning. arXiv preprint arXiv: 1312.5602, 2013.
|
| [25] |
Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning. Nature, 2015, 518(7540): 529-533. DOI:10.1038/nature14236 |
| [26] |
Van Hasselt H, Guez A, Silver D. Deep reinforcement learning with double Q-learning. Proceedings of the 30th AAAI Conference on Artificial Intelligence. Phoenix, AZ, USA. 2016. 2094–2100.
|
| [27] |
Schaul T, Quan J, Antonoglou I, et al. Prioritized experience replay. Proceedings of the 2016 International Conference on Learning Representations. San Juan, UT, USA. 2016. 1–21.
|
| [28] |
Wang ZY, Schaul T, Hessel M, et al. Dueling network architectures for deep reinforcement learning. Proceedings of the 33rd International Conference on International Conference on Machine Learning. New York, NY, USA. 2016. 1995–2003.
|
| [29] |
Fortunato M, Azar MG, Piot B, et al. Noisy networks for exploration. arXiv preprint arXiv: 1706.10295, 2017.
|
| [30] |
Bellemare MG, Dabney W, Munos R. A distributional perspective on reinforcement learning. Proceedings of the 34th International Conference on Machine Learning. Sydney, NSW, Australia. 2017. 449–458.
|
| [31] |
Hessel M, Modayil J, Van Hasselt H, et al. Rainbow: Combining improvements in deep reinforcement learning. Proceedings of the 32nd AAAI Conference on Artificial Intelligence. New Orleans, LA, USA. 2018. 3215–3222.
|
| [32] |
Williams RJ. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine Learning, 1992, 8(3–4): 229-256. DOI:10.1007/BF00992696 |
| [33] |
Schulman J, Levine S, Moritz P, et al. Trust region policy optimization. Proceedings of the 31st International Conference on Machine Learning. Lille, France. 2015. 1889–1897.
|
| [34] |
Schulman J, Wolski F, Dhariwal P, et al. Proximal policy optimization algorithms. arXiv preprint arXiv: 1707.06347, 2017.
|
| [35] |
Konda VR, Tsitsiklis JN. On actor-critic algorithms. SIAM Journal on Control and Optimization, 2003, 42(4): 1143-1166. |
| [36] |
Mnih V, Badia AP, Mirza M, et al. Asynchronous methods for deep reinforcement learning. Proceedings of the 33rd International Conference on International Conference on Machine Learning. New York, NY, USA. 2016. 1928–1937.
|
| [37] |
Silver D, Lever G, Heess N, et al. Deterministic policy gradient algorithms. Proceedings of the 31st International Conference on International Conference on Machine Learning. Beijing, China. 2014. 387–395.
|
| [38] |
Lillicrap TP, Hunt JJ, Pritzel A, et al. Continuous control with deep reinforcement learning. 4th International Conference on Learning Representations. San Juan, UT, USA. 2016.
|
| [39] |
Fujimoto S, Van Hoof H, Meger D. Addressing function approximation error in actor-critic methods. Proceedings of the 35th International Conference on Machine Learning. Stockholm, Sweden. 2018. 1587–1596.
|
| [40] |
Haarnoja T, Zhou A, Abbeel P, et al. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. Proceedings of the 35th International Conference on Machine Learning. Long Beach, CA, USA. 2018. 1861–1870.
|
| [41] |
Arulkumaran K, Deisenroth MP, Brundage M, et al. Deep reinforcement learning: A brief survey. IEEE Signal Processing Magazine, 2017, 34(6): 26-38. DOI:10.1109/MSP.2017.2743240 |
| [42] |
Gomez F, Schmidhuber J. Evolving modular fast-weight networks for control. Proceedings of the 15th International Conference on Artificial Neural Networks: Formal Models and their Applications. Berlin, Germany. 2005. 383–389.
|
| [43] |
Koutník J, Cuccu G, Schmidhuber J, et al. Evolving large-scale neural networks for vision-based reinforcement learning. Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation. Amsterdam, the Netherland. 2013. 1061–1068.
|
| [44] |
Kakade S. A natural policy gradient. Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic. Cambridge, UK. 2001. 1531–1538.
|
| [45] |
Heess N, Dhruva TB, Sriram S, et al. Emergence of locomotion behaviours in rich environments. arXiv preprint arXiv: 1707.02286, 2017
|
| [46] |
Duan Y, Schulman J, Chen X, et al. RL2: Fast reinforcement learning via slow reinforcement learning. arXiv preprint arXiv: 1611.02779, 2016.
|
| [47] |
Finn C, Abbeel P, Levine S. Model-agnostic meta-learning for fast adaptation of deep networks. Proceedings of the 34th International Conference on Machine Learning. Sydney, Australia. 2017. 1126–1135.
|
| [48] |
Gupta A, Mendonca R, Liu YX, et al. Meta-reinforcement learning of structured exploration strategies. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Red Hook, NY, USA. 2018. 5307–5316.
|
| [49] |
Mendonca R, Gupta A, Kralev R, et al. Guided meta-policy search. Advances in Neural Information Processing Systems 32. Vancouver, Canada. 2019.
|
| [50] |
OpenAI: Benchmarks for spinning up implementations. https://spinningup.openai.com/en/latest/spinningup/bench.html#hopper-pytorch-versions. 2018.
|
| [51] |
Foerster JN. Deep multi-agent reinforcement learning [Ph.D Thesis]. Oxford: University of Oxford, 2018.
|
| [52] |
Chen X, Deng XT. Settling the complexity of two-player nash equilibrium. 2006 47th Annual IEEE Symposium on Foundations of Computer Science. Berkeley, CA, USA. 2006. 261–272.
|
| [53] |
Busoniu L, Babuska R, De Schutter B. A comprehensive survey of multiagent reinforcement learning. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2008, 38(2): 156-172. |
| [54] |
Foerster JN, Assael YM, De Freitas N, et al. Learning to communicate with deep multi-agent reinforcement learning. Proceedings of the 30th International Conference on Neural Information Processing Systems. Red Hook, NY, USA. 2016. 2145–2153.
|
| [55] |
杜威, 丁世飞. 多智能体强化学习综述. 计算机科学, 2019, 46(8): 1-8. DOI:10.11896/j.issn.1002-137X.2019.08.001 |
| [56] |
Littman ML. Markov games as a framework for multi-agent reinforcement learning. In: Cohen WW, Hirsh H, eds. Machine Learning Proceedings 1994. Amsterdam: Elsevier, 1994. 157–163.
|
| [57] |
Hu JL, Wellman MP. Nash Q-learning for general-sum stochastic games. Journal of Machine Learning Research, 2004, 4(6): 1039-1069. DOI:10.1162/1532443041827880 |
| [58] |
Littman ML. Friend-or-foe Q-learning in general-sum games. Proceedings of the Eighteenth International Conference on Machine Learning. San Francisco, CA, USA. 2001. 322–328.
|
| [59] |
Tan M. Multi-agent reinforcement learning: Independent vs. Cooperative agents. Proceedings of the Tenth International Conference. Amherst, MA, USA. 1993. 330–337.
|
| [60] |
Lowe R, Wu Y, Tamar A, et al. Multi-agent actor-critic for mixed cooperative-competitive environments. Proceedings of the 31st International Conference on Neural Information Processing Systems. Red Hook, NY, USA. 2017. 6382–6393.
|
| [61] |
Foerster JN, Farquhar G, Afouras T, et al. Counterfactual multi-agent policy gradients. The 32th AAAI Conference on Artificial Intelligence. New Orleans, LA, USA. 2018. 2974–2982.
|
| [62] |
Sunehag P, Lever G, Gruslys A, et al. Value-decomposition networks for cooperative multi-agent learning based on team reward. The 17th International Conference on Autonomous Agents and Multiagent Systems. Stockholm, Sweden. 2018. 2085–2087.
|
| [63] |
Rashid T, Samvelyan M, De Witt CS, et al. QMIX: Monotonic value function factorisation for deep multi-agent reinforcement learning. Proceedings of the 35th International Conference on Machine Learning. Stockholm, Sweden. 2018. 4295–4304.
|
| [64] |
Yang YD, Luo R, Li MN, et al. Mean field multi-agent reinforcement learning. arXiv preprint arXiv: 1802.05438, 2018.
|
| [65] |
Finn C. Learning to learn with gradients [Ph.D Thesis]. Berkeley: University of California, 2018.
|
| [66] |
Wang JX, Kurth-Nelson Z, Tirumala D, et al. Learning to reinforcement learn. arXiv preprint arXiv: 1611.05763, 2016.
|
| [67] |
Vuorio R, Sun SH, Hu HX, et al. Multimodal model-agnostic meta-learning via task-aware modulation. Advances in Neural Information Processing Systems (NIPS 2019). Vancouver, BC, Canada. 2019. 1–12.
|
| [68] |
Nagabandi A, Clavera I, Liu SM, et al. Learning to adapt in dynamic, real-world environments through meta-reinforcement learning. arXiv preprint arXiv: 1803.11347v6, 2019.
|
| [69] |
Duan Y, Andrychowicz M, Stadie BC, et al. One-shot imitation learning. Proceedings of the 31st Conference on Neural Information Processing Systems. Long Beach, CA, USA. 2017. 1087–1098.
|
| [70] |
Finn C, Yu TH, Zhang TH, et al. One-shot visual imitation learning via meta-learning. arXiv preprint arXiv: 1709.04905, 2017.
|
| [71] |
Yu TH, Finn C, Dasari S, et al. One-shot imitation from observing humans via domain-adaptive meta-learning. 6th International Conference on Learning Representations. Vancouver, BC, Canada. 2018.
|
| [72] |
Xu K, Ratner E, Dragan A, et al. Learning a prior over intent via meta-inverse reinforcement learning. arXiv preprint arXiv: 1805.12573, 2018.
|
| [73] |
Xie AN, Singh A, Levine S, et al. Few-shot goal inference for visuomotor learning and planning. Proceedings of the 2nd Conference on Robot Learning. Zurich, Switzerland. 2018. 40–52.
|
| [74] |
Rakelly K, Zhou A, Quillen D, et al. Efficient off-policy meta-reinforcement learning via probabilistic context variables. arXiv preprint arXiv: 1903.08254v1, 2019.
|
| [75] |
Silver D, Schrittwieser J, Simonyan K, et al. Mastering the game of go without human knowledge. Nature, 2017, 550(7676): 354-359. DOI:10.1038/nature24270 |
| [76] |
Silver D, Hubert T, Schrittwieser J, et al. A general reinforcement learning algorithm that masters chess, shogi, and go through self-play. Science, 2018, 362(6419): 1140-1144. DOI:10.1126/science.aar6404 |
| [77] |
Browne CB, Powley E, Whitehouse D, et al. A survey of Monte Carlo tree search methods. IEEE Transactions on Computational Intelligence and AI in Games, 2012, 4(1): 1-43. DOI:10.1109/tciaig.2012.2186810 |
| [78] |
Neller TW, Hnath S. Approximating optimal dudo play with fixed-strategy iteration counterfactual regret minimization. Proceedings of the 13th International Conference on Advances in Computer Games. Berlin, Germany. 2012. 170–183.
|
| [79] |
OpenAI Five 2016–2019. https://openai.com/projects/five/.
|
| [80] |
Mülling K, Kober J, Kroemer O, et al. Learning to select and generalize striking movements in robot table tennis. The International Journal of Robotics Research, 2013, 32(3): 263-279. DOI:10.1177/0278364912472380 |
| [81] |
谢天瑞. 基于强化学习的D2D智能组网[硕士学位论文]. 北京: 北京邮电大学, 2018.
|
| [82] |
Mirowski P, Pascanu R, Viola F, et al. Learning to navigate in complex environments. arXiv preprint arXiv: 1611.03673, 2017.
|
| [83] |
Banino A, Barry C, Uria B, et al. Vector-based navigation using grid-like representations in artificial agents. Nature, 2018, 557(7705): 429-433. DOI:10.1038/s41586-018-0102-6 |
| [84] |
Liu CL, Tomizuka M. Algorithmic safety measures for intelligent industrial co-robots. 2016 IEEE International Conference on Robotics and Automation. Stockholm, Sweden. 2016. 3095–3102.
|
| [85] |
Liu CL, Tomizuka M. Designing the robot behavior for safe human-robot interactions. In: Wang Y, Zhang YM, eds. Trends in Control and Decision-Making for Human-Robot Collaboration Systems. Cham: Springer, 2017. 241–270.
|
| [86] |
Bazzan ALC, Klügl F. Introduction to intelligent systems in traffic and transportation. Synthesis Lectures on Artificial Intelligence and Machine Learning, 2014, 7(3): 1-137. |
| [87] |
杨文臣, 张轮, Zhu F. 多智能体强化学习在城市交通网络信号控制方法中的应用综述. 计算机应用研究, 2018, 35(6): 1613-1618. DOI:10.3969/j.issn.1001-3695.2018.06.003 |
| [88] |
Chu TS, Wang J, Codecà L, et al. Multi-agent deep reinforcement learning for large-scale traffic signal control. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(3): 1086-1095. |
| [89] |
Belletti F, Haziza D, Gomes G, et al. Expert level control of ramp metering based on multi-task deep reinforcement learning. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(4): 1198-1207. DOI:10.1109/TITS.2017.2725912 |
| [90] |
Tesla vehicle deliveries and autopilot mileage statistics. https://lexfridman.com/tesla-autopilot-miles-and-vehicles/.
|
| [91] |
Fridman L, Terwilliger J, Jenik B. DeepTraffic: Crowdsourced hyperparameter tuning of deep reinforcement learning systems for multi-agent dense traffic navigation. Proceedings of the 32nd Conference on Neural Information Processing Systems. Montréal, QC, Canada. 2018.
|
| [92] | |
| [93] |
O’Kelly M, Sinha A, Namkoong H, et al. Scalable end-to-end autonomous vehicle testing via rare-event simulation. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Red Hook, NY, USA. 2018. 9849–9860.
|
| [94] |
Tang XC, Qin ZW, Zhang F, et al. A deep value-network based approach for multi-driver order dispatching. Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. Anchorage, AK, USA. 2019. 1780–1790.
|
| [95] |
Xu Z, Li ZX, Guan QW, et al. Large-scale order dispatch in on-demand ride-hailing platforms: A learning and planning approach. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. London, UK. 2018. 905–913.
|
| [96] |
Zhao XY, Xia L, Tang JL, et al. Deep reinforcement learning for search, recommendation, and online advertising: A survey. ACM SIGWEB Newsletter, 2019, 4. DOI:10.1145/3320496.3320500 |
| [97] |
Yin DW, Hu YN, Tang JL, et al. Ranking relevance in yahoo search. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco, CA, USA. 2016. 323–332.
|
| [98] |
Wei W, Xu J, Lan YY, et al. Reinforcement learning to rank with markov decision process. Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval. Shinjuku, Japan. 2017. 945–948.
|
| [99] |
Zhang S, Yao LN, Sun AX, et al. Deep learning based recommender system: A survey and new perspectives. ACM Computing Surveys, 2019, 52(1): 5. DOI:10.1145/3285029 |
| [100] |
Zhao XY, Zhang L, Ding ZY, et al. Recommendations with negative feedback via pairwise deep reinforcement learning. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. London, UK. 2018. 1040–1048.
|
| [101] |
Wu D, Chen C, Yang X, et al. A multi-agent reinforcement learning method for impression allocation in online display advertising. arXiv preprint arXiv: 1809.03152, 2019.
|
 2020, Vol. 29
2020, Vol. 29



