2. 南京邮电大学, 南京 210023;
3. 国电南瑞南京控制系统有限公司, 南京 211106
2. Nanjing University of Posts and Telecommunications, Nanjing 210023, China;
3. Guodian NARI Nanjing Control System Co. Ltd., Nanjing 211106, China
随着现代化工业的不断发展, 随之而来的是对各种资源的巨大需求[1]. 经济结构的发展也推动了能源消费结构的改变, 以自动控制系统、先进的材料技术、灵活的制造工艺等新技术为基础的可调资源发电技术在负荷调控及优化方面发挥着重要作用. 如何利用可调资源实现横向多源互补、纵向源-网-荷-储协调的台区下多源协调优化调度, 促进电网供需平衡, 减少终端用户电费支出、降低电力公司成本、节约资源、减少环境污染, 同时减少社会对电力建设的投入是今后研究重点.
文献[2]提出以提高风电消纳能力为目标, 考虑源荷多时间尺度的优化调度策略, 构建了源荷储协同调度模型, 并通过算例验证了所提策略的有效性; 文献[3]基于分布式算法提出了一种考虑风光火储和可调控负荷的多区域调度优化模型, 并通过算例验证电储能装置和可调控负荷的参与, 能够降低区域互联系统对发电机组的备用要求, 提高系统的备用能力; 文献[4]提出了以成本最优和设备输出功率调整量最小为混合目标, 建立了多时间尺度的优化调度模型, 该模型可以保证综合能源系统的经济性运行, 又能减轻电网平抑功率波动负担; 文献[5]提出了一种变频空调负荷虚拟同步机群参与微网调频的控制方法, 并验证了负荷虚拟同步机化改造能够有效提升空调负荷参与调频的能力; 文献[6]运用模糊综合评估法构建了多能互补综合能源优化利用评估体系, 并通过算例进行验证, 为多种能源的综合利用提供科学、准确的依据. 上述文献主要从源-网-荷等不同角度开展研究, 对台区下的资源调控与优化有借鉴意义, 但是基于模型预测控制的台区下多源分层分布式协调优化研究相对较少. 本文通过分析台区下资源分层分布式协调运行典型场景, 对分布式电源、储能以及各种辅助设备进行建模, 以成本、效益、新能源消纳率、节能等多目标出发解析不同场景下供能设备的出力情况及储能设备的运行状态; 通过建立基于模型预测控制的分层分布式协调优化模型, 根据协调优化模型开发基于模型预测控制的多源协调优化模型的求解方法, 并通过算例验证该模型的有效性, 为可调资源利用奠定基础.
1 台区下资源分层分布式协调运行典型场景与电网友好互动能够实现对可调资源的优化利用, 而且能够减少分布式能源对配电网的不利影响[7-11].
1.1 场景1. 多源自治运行控制模式自治模式如图1所示. 按照效率最高、经济最优原则, 在安全约束条件下, 自治模式调控中心向各区域下发调控目标, 按照要求各区域进行可调资源的就地消纳, 把运行成本最低作为约束目标进行优化, 同时调控中心以数据平台为依靠, 监测区域负荷和能源状态, 以及网络安全约束校验. 在场景1条件下, 各个区域之间没有负荷以及能量的交互, 因此调控措施受到限制, 如下图的应用场景中, 区域1、2、3之间的调控之间相互没有干扰, 不存在能量与负荷的交互.

|
图 1 自治模式应用场景 |
在该模式下不能够完成区域内能量相互平衡下, 那么为了保持能量平衡, 就会进入场景2, 调度区域之间的能量来实现总能量平衡.
1.2 场景2. 多源协同优化调度模式在网络安全约束为前提的条件下, 各区域在调度中心的统一安排下实现负荷或者能量的转移, 同时监测和展示各个区域负荷和能源状态. 在该调度模式下, 能够执行的调控措施多种多样. 而且每个地区的能源补给与使用的预测、客户用能情况以及调控策略等信息能够实现全局共享、跨能量路由器的潮流调度. 如图2所示为多源协同优化调度模式下的场景, 区域1, 2, 3之间通过主动配电网实现电能的交互.

|
图 2 多源协同优化模式应用场景 |
2 分层分布式协调运行优化建模
通过设立分层分布式优化调度机制, 分别为区域Agent层、局部Agent层, Agent层以主动配电网为核心, 综合各种分布式发电及蓄电设备、分布式冷热能产生和储存设备等, 通过分层多源协调优化调度架构将整个优化模型的目标和约束分散到每一个Agent层, 利用Agent层之间的相互联系及从属关系, 通过主动配电网引导各个区域进行分布式优化调度, 实现可调资源间的相互转换及能源的协调优化控制.
每个区域根据主动配电网下发的调度激励信号, 区域内的各局部Agent: 电源、冷热电负荷、冷热电储能设备及冷热电能源相互转换的辅助设备等, 在满足主动配电网下发的调度目标后, 以总体成本最低为优化目标函数, 实现各个局部Agent的优化调度, 实现区域内部的能量自治平衡.
2.1 目标函数(1)局部Agent层
1)经济效益最优
本文所提出的可调资源优化配置的综合总成本由电网交互的功率成本、设备初始投资、燃料成本、系统运行维护成本组成.
| $\min {f_1} = {C_{\inf }} + {C_{\rm fuel}} + {C_{\rm om}} + {C_{\rm grid}}$ | (1) |
其中, Cgrid为微电网与电网交换的功率成本; Cinf设备初始投资年等值成本; Com为系统设备运行成本; Cfuel为系统燃料成本.
| $\begin{split} {C_{\inf }} = & R \cdot ({P_{\rm cap,GT}}\; \cdot \;{C_{\rm GT}} + {P_{\rm cap,TST}} \cdot {C_{\rm TST}} + {P_{\rm cap,GB}} \cdot {C_{\rm GB}} \\ & + {Q_{\rm cap,AC}} \cdot {C_{\rm AC}}+ {Q_{\rm cap,EC}} \cdot {C_{\rm EC}} + {P_{\rm cap,pv}} \cdot {C_{\rm pv}}\\ & + {P_{\rm cap,BT}} \cdot {C_{\rm BT}}) \\ \end{split} $ | (2) |
| $R = \dfrac{{r{{(1 + r)}^n}}}{{{{(1 + r)}^n} - 1}}$ | (3) |
其中, CTST为蓄热槽单位容量成本; CAC为吸收式制冷机的单位容量成本; CGB为燃气锅炉的单位容量成本; CGT为燃气轮机的投资单位容量成本; CEC为电制冷机单位容量成本; C BT为蓄电池单位容量成本; CPV为光伏电池单位容量成本; 下标cap表示设备额定容量; R为资金年回收率; r为折现率, 表现为加权平均资本成本, 是来测算投资方案的净现值和净现值系数, 实现投资决策; n为设备使用年限.
系统燃料费用包括燃气轮机燃料费用和燃气锅炉燃料费用:
| ${C_{\rm fuel}} = \sum\limits_{j = 1}^M {\sum\limits_{t = 1}^T {\left[ {{F_{\rm GT}}({P_{{\rm GT},j}}\left( t \right)) + {F_{\rm GB}}({P_{{\rm GB},j}}\left( t \right))} \right]} } \cdot {d_j}$ | (4) |
系统运行维护费用包括主要设备维护费如式(5).
| $\begin{split} &{C_{\rm om}} =\\ & \sum\limits_{j = 1}^M {\sum\limits_{t = 1}^T {\left[ {K_{\rm om,GT}} \!\cdot \!{P_{{\rm GT},j}}\left( t \right) \!+\! {K_{\rm om,GB}} \!\cdot \! {Q_{{\rm GB},j}}\left( t \right)\!+ \! {K_{\rm om,TST}} \!\cdot \!|{Q_{{\rm TST},j}}\left( t \right)|\! +\! {K_{\rm om,AC}} \cdot {Q_{{\rm AC},j}}\left( t \right) \!+\! {K_{\rm om,EC}} \!\cdot \!{Q_{{\rm EC},j}}\left( t \right) \!+\! {K_{\rm om,BT}} \cdot |{P_{{\rm BT},j}}\left( t \right)| \right]} } \! \cdot \!{d_j} \end{split}$ | (5) |
系统与大电网交互费用为式(6).
| ${C_{\rm grid}} = \sum\limits_{j = 1}^M {\sum\limits_{t = 1}^T {\left[ ({C_{\rm ph}} + \gamma {C_{\rm se}})/2 \cdot {P_{{\rm ex},j}}\left( t \right) +({C_{\rm ph}} - \gamma {C_{\rm se}})/2 \cdot \left| {{P_{{\rm ex},j}}\left( t \right)} \right| \right]} } \cdot {d_j}$ | (6) |
其中, T表示系统在典型日运行小时数; Kom,i系统设备运行维护费用; dj表示典型日运行天数; M表示第几个典型日; γ值为0或1, 当γ=1时, 表示微电网通过售电给主网获得收益, 当γ=0时, 表示微电网不向主网收取售电功率费用, Pex,j(t)小于0表示微网向电网输出电量, 大于0时表示微网从电网购电; Cph和Cse分别为微电网购售电费用.
2)绿色节能最优
为了减低能源浪费, 提高单位能耗国内生产总值, 以一次能源消耗量最小为目标函数.
| $\min {f_{\rm{2}}} = \left\{ \begin{split} &\sum\limits_{j = 1}^M {\sum\limits_{t = 1}^T {\left[ {P_{{\rm ex},j}}\left( t \right) \cdot {\mu _e} + ({F_{{\rm GT},j}}\left( t \right) + {F_{{\rm GB},j}}\left( t \right)) \cdot {\mu _f} \right]} } \cdot {d_j},\;\; {P_{{\rm ex},j}}\left( t \right) > 0\\ &\sum\limits_{j = 1}^M {\sum\limits_{t = 1}^T {\left[ ({F_{{\rm GT},j}}\left( t \right) + {F_{{\rm GB},j}}\left( t \right)) \cdot {\mu _f} \right]} } \cdot {d_j},\;\; {P_{{\rm ex},j}}\left( t \right) \le 0\\ \end{split} \right.$ | (7) |
其中, μf为天然气一次能源转换系数; μe为电网一次能源转换系数; Pex为系统向电网购买电量[12].
3)新能源消纳率最大
新能源消纳率指的是光伏电池、风机等不可控分布式电源出力的实际利用效率, 它表示为参与系统优化调度的分布式电源出力与实际机组可调度的最大功率的比值, 用以下公式来表示:
| $\min {f_{\rm{3}}} = \dfrac{1}{{24}}\sum\limits_{t = 1}^{24} \left({\frac{{P_t^{WT} + P_t^{ PV}}}{{P_{t,{\rm sche}}^{WT} + P_{t,{\rm sche}}^{PV}}}} \right)$ | (8) |
| $\left\{\begin{array}{*{20}{l}} P_t^{WT} = \displaystyle\sum\limits_{i = 1}^M {P_t^{wt,{\rm zon},i}} ,P_{t,{\rm sche}}^{WT} = \displaystyle\sum\limits_{i = 1}^M {P_{t,{\rm sche}}^{wt,{\rm zon},i}} \\ P_t^{PV} = \displaystyle\sum\limits_{i = 1}^M {P_t^{pv,{\rm zon},i}} ,P_{t,{\rm sche}}^{PV} = \displaystyle\sum\limits_{i = 1}^M {P_{t,{\rm sche}}^{pv,{\rm zon},i}} \end{array} \right.$ | (9) |
其中,
(2)电源Agent层:
电源Agent层优化目标为发电的经济成本最低.
| $\begin{split} {\rm Min}(&{\rho _{\rm wind}} \times {P_{\rm wind}} + {\rho _{\rm GT}} \times {P_{\rm GT}} \\ &+{\rho _{\rm Sun}} \times {P_{\rm Sun}} + {\rho _{\rm ES}} \times {P_{\rm ES}}),\;t \in {N_t} \end{split}$ | (10) |
| $\begin{split} {P_{joi}}(t) =& {P_{\rm Wind}}(t) + {P_{\rm WES,dis}}(t) - {P_{\rm WES,ch}}(t) + {P_{\rm Sun}}(t) \\ &+ {P_{\rm SES,dis}}(t) - {P_{\rm SES,ch}}(t) + {P_{\rm GT}}(t) \end{split}$ | (11) |
| $\left\{\begin{array}{l} 0 \le {P_{\rm RDG}}(t) \le P_{_{\rm RDG}}^{\max }(t) \\ 0 \le {P_{\rm ES,ch}}(t) \le P_{_{\rm ES,ch}}^{\max }(t) \\ 0 \le {P_{\rm ES,ch}}(t) \le P_{_{\rm ES,ch}}^{\max } \\ 0 \le {P_{\rm ES,dis}}(t) \le P_{_{\rm ES,dis}}^{\max } \\ {P_{\rm ES,ch}}(t) \cdot {P_{\rm ES,dis}}(t) = 0 \end{array} \right.$ | (12) |
| $\begin{split} {E_{\rm ES}}(t + 1) = {E_{\rm ES}}(t) + {P_{\rm ES,ch}}(t){\eta _{\rm ES,ch}}\Delta t - \dfrac{{{P_{\rm ES,dis}}(t)}}{{{\eta _{\rm ES,dis}}}}\Delta t \end{split}$ | (13) |
| $E_{\rm ES}^{\min } \le {E_{\rm ES}}(t) \le E_{\rm ES}^{\max }$ | (14) |
| $|{E_{\rm ES}}(t) - {E_{\rm ES}}(0)| \le {\varepsilon _{\rm ES}}$ | (15) |
式中,
台区柔性可调资源往往包含了区域范围内冷能、热能、电能等多种形式能源的生产、传输、转换、消费过程, 因此设置电能平衡约束、冷平衡约束、热平衡约束. 由于本文所提出的可调资源优化配置的综合总成本包含由电网交互的功率成本, 因此要设置与主网交互功率和电压约束条件.
(1)电能平衡等式约束
电能平衡主要由燃气轮机、蓄电池、光伏发电、风力发电和电网满足电负荷和驱动地源热泵、户用空调, 蓄电池的有充放电两种模式, 因此电能平衡方程如下:
蓄电池放电公式如式(16).
| $ {P_{{\rm GT},j}}\left( t \right) + {P_{pv,j}}\left( t \right) + P_{_{{\rm BT},j}}^{\rm disch}\left( t \right) \cdot \eta _{BT}^{\rm disch} + {P_{{\rm wind},j}}\left( t \right) + {P_{\rm grid}}(t) = {P_{{\rm aircon},j}}\left( t \right) + {P_{{\rm pump},j}}(t) + {P_{e,j}}\left( t \right) \\ $ | (16) |
蓄电池充电公式如式(17).
| $ {P_{{\rm GT},j}}\left( t \right) + {P_{pv,j}}\left( t \right) + P_{_{{\rm BT},j}}^{ch}\left( t \right)/\eta _{\rm BT}^{ch} + {P_{{\rm wind},j}}\left( t \right) + {P_{\rm grid}}(t)= {P_{{\rm aircon},j}}\left( t \right) + {P_{{\rm pump},j}}(t) + {P_{e,j}}\left( t \right) $ | (17) |
(2)热能平衡不等式约束
热能平衡主要由燃气锅炉、地源热泵和电储热锅炉满足热负荷的需求, 电储热锅炉有充放热两种模式, 因此热能平衡方程如下:
电储热锅炉放热:
| $ {Q_{{\rm gasboil},j}}\left( t \right) \cdot {\eta _{\rm rec}} + {Q_{{\rm disch},j}}\left( t \right) \cdot \eta _{\rm TST}^{\rm disch} + {Q_{{\rm pump},j}}\left( t \right) \ge {Q_{h,j}}\left( t \right) \\ $ | (18) |
电储热锅炉蓄热:
| ${Q_{{\rm gasboil},j}}\left( t \right) \cdot {\eta _{\rm rec}} + {Q_{{\rm{ch}},j}}\left( t \right)/\eta _{\rm TST}^{\rm ch} + {Q_{{\rm pump},j}}\left( t \right) \ge {Q_{h,j}}\left( t \right) $ | (19) |
(3)冷能平衡等式约束
冷能平衡主要由空调、地源热泵和冰蓄冷满足冷负荷的需求, 冰蓄冷有蓄放冷两种模式, 因此冷能平衡方程如下:
冰蓄冷放冷:
| ${Q_{{\rm aircon},j}}\left( t \right) \cdot {\eta _{\rm rec}} + {Q_{{\rm disch},j}}\left( t \right) \cdot \eta _{{\rm{TST}}}^{\rm disch}+ {Q_{{\rm pump},j}}\left( t \right) \ge {Q_{h,j}}\left( t \right) $ | (20) |
冰蓄冷蓄冷:
| ${Q_{{\rm aircon},j}}\left( t \right) \cdot {\eta _{\rm rec}} + {Q_{{\rm{ch}},j}}\left( t \right)/\eta _{\rm TST}^{{\rm{ch}}} +{Q_{{\rm pump},j}}\left( t \right) \ge {Q_{h,j}}\left( t \right)$ | (21) |
(4)与主网交互功率和电压约束
| $P_{\rm ex}^{\min } \le {P_{{\rm ex},j}}\left( t \right) \le P_{\rm ex}^{\max }$ | (22) |
其中,
| ${U_{\min }} \le U(t) \le {U_{\max }}$ | (23) |
式中,
针对本文分层分布式协调运行优化模型, 以模型预测控制作为优化算法, 可以更大限度地消除微电网中不确定性因素对优化运行调度方案的影响. 通过状态空间模型建立起预测控制, 推导基于状态空间模型的预测方程.
多源协调优化模型求解依据储能SOC和功率平衡方程, 把储能SOC、储能充放电功率、区域互联网与外电网的联络线交换功率和可调度机组出力构成的向量作为状态向量:
| $x(k) = {[{P_{\rm MT}}(k),{P_{\rm FC}}(k),{P_{\rm bat}}(k),{S_B}(k),{P_{\rm grid}}(k)]^{\rm T}}$ | (24) |
以可调度机组和储能的出力增量构成向量为控制变量:
| $u(k) = {[\Delta {P_{\rm MT}}(k),\Delta {P_{\rm FC}}(k),\Delta {P_{\rm grid}}(k)]^{\rm T}}$ | (25) |
以负荷、风电机组及光伏的超短期预测功率增量构成的向量为扰动输入:
| $r(k) = {[\Delta {P_{\rm load}}(k),\Delta {P_{\rm wind}}(k),\Delta {P_{\rm PV}}(k)]^{\rm T}}$ | (26) |
以联络线交换功率和储能SOC构成的向量为输出变量:
| $y(k) = {[{P_{\rm grid}}(k),{S_B}(k)]^{\rm T}}$ | (27) |
建立多输入、多输出状态空间模型如式(28)、式(29).
| $\begin{split} x(k + \Delta t) = &\left[\begin{array}{*{20}{c}} {{P_{\rm MT}}(k + \Delta t)} \\ {{P_{\rm FC}}(k + \Delta t)} \\ {{P_{\rm bat}}(k + \Delta t)} \\ {{S_B}(k + \Delta t)} \\ {{P_{\rm grid}}(k + \Delta t)} \end{array}\right] = \left[\begin{array}{*{20}{c}} 1&0&0&0&0 \\ 0&1&0&0&0 \\ 0&0&1&0&0 \\ 0&0&{ - \dfrac{{\Delta t}}{{{E_{bat}}}}}&{1 - \sigma }0&0\\ 0&0&0&0&1 \end{array}\right]\left[\begin{array}{*{20}{c}} {{P_{\rm MT}}(k)} \\ {{P_{\rm FC}}(k)} \\ {{P_{\rm bat}}(k)} \\ {{S_B}(k)} \\ {{P_{\rm grid}}(k)} \end{array}\right] + \left[\begin{array}{*{20}{c}} 1&0&0 \\ 0&1&0 \\ 0 &0&1\\ 0&0&{ - \dfrac{{\Delta t}}{{{E_{bat}}}}} \\ { - 1}&{ - 1}&{ - 1} \end{array}\right]\left[\begin{array}{*{20}{c}} {\Delta {P_{\rm MT}}(k)} \\ {\Delta {P_{\rm FC}}(k)} \\ {\Delta {P_{\rm bat}}(k)} \end{array}\right]\\ & + \left[\begin{array}{*{20}{c}} 0&0&0 \\ 0&0&0 \\ 0&0&0 \\ 0&0&0 \\ 1&{ - 1}&{ - 1} \end{array}\right]\left[\begin{array}{*{20}{c}} {\Delta {P_{\rm load}}(k)} \\ {\Delta {P_{\rm wind}}(k)} \\ {\Delta {P_{\rm PV}}(k)} \end{array}\right] \\ \end{split} $ | (28) |
| $\begin{gathered} y(k) = \left[\begin{array}{*{20}{c}} {{P_{\rm grid}}(k)} \\ {S{}_B(k)} \end{array}\right] = \left[\begin{array}{*{20}{c}} 0&0&0&0&1 \\ 0&0&0&1&0 \end{array}\right] \cdot \left[\begin{array}{*{20}{c}} {{P_{\rm MT}}(k)}&{{P_{\rm FC}}(k)}&{{P_{\rm bat}}(k)}&{{S_B}(k)}&{{P_{\rm grid}}(k)} \end{array}\right]{^{\rm{T}}} \\ \end{gathered} $ | (29) |
由式(27)和式(28)可知, 通过对该状态空间预测模型反复迭代, 并基于可再生能源和负荷超短期功率预测数据, 直到相前预测p步, 获得储能SOC和联络线在预测时长
| $\begin{split} & {Y_t} \!\!= \!\! \left[P_{\rm grid}^f(k \!\!+\!\! \Delta t),S_B^f(k \!\!+ \!\!\Delta t),\cdots,P_{\rm grid}^f(k\!\! +\!\! p\Delta t),S_B^f(k \!\!+\!\! p\Delta t)\right] \\ \end{split} $ | (30) |
为应对可再生能源和负荷日前预测导致的联络线功率波动, 保证储能在日内调度中遵循日运行能量平衡的约束, 并且确保联络线功率跟踪日前计划值, 在当前时刻向前
| ${R_{da}} = {\left[ \begin{gathered} P_{grid}^{ref}(k + \Delta t),S_B^{ref}(k + \Delta t) \\ \cdots \\ P_{grid}^{ref}(k + p\Delta t),S_B^{ref}(k + p\Delta t) \\ \end{gathered} \right]^{\rm{T}}}$ | (31) |
然后以目标为它们之间的误差最小, 而且还要保证各机组控制调节增量尽可能的小, 于是能够把对应的滚动优化调度转化为二次规划问题.
目标函数:
| $\min J = {({R_{\rm da}} - {Y_f})^{\rm{T}}}{W_{\rm err}}({R_{\rm da}} - {Y_f}) + {U^{\rm{T}}}{Q_u}U$ | (32) |
约束条件:
| $\left\{\begin{array}{l} \Delta P_{\rm MT}^{\min } \le \Delta P_{\rm MT}^t \le \Delta P_{\rm MT}^{\max } \\ P_{\rm MT}^{\min } \le P_{\rm MT}^t \le P_{\rm MT}^{\max } \\ \Delta P_{\rm FC}^{\min } \le \Delta P_{\rm FC}^t \le \Delta P_{\rm FC}^{\max } \\ P_{\rm FC}^{\min } \le P_{\rm FC}^t \le P_{\rm FC}^{\max } \\ \Delta P_{\rm bat}^{\min } \le \Delta P_{\rm bat}^t \le \Delta P_{\rm bat}^{\max } \\ P_{\rm bat}^{\min } \le P_{\rm bat}^t \le P_{\rm bat}^{\max } \\ S_B^{\min } \le S_B^t \le S_B^{\max } \end{array}\right. $ | (33) |
其中,
然后通过利用Matlab优化工具箱的quadprog函数求解模型.
4 算例分析 4.1 算例描述为充分验证上述基于模型预测控制算法进行多源协调优化模型的求解, 本节选取综合能源片区的3个典型多能源互联系统进行案例分析, 各区域内均有居民用户, 商业用户和工业用户, 按照前述的光伏预测法, 得到光伏的出力曲线, 按照前述的聚类分析法, 得到用户负荷曲线.
各区域的设备配置如表1所示, 分布式电源设备有微型燃气轮机、光伏发电、风力发电, 制冷设备有空调、热泵, 制热设备有燃气锅炉和热泵, 蓄能设备有蓄电池、电储热锅炉和冰蓄冷. 分时电价如表2所示.
| 表 1 设备参数表 |
| 表 2 分时电价表 |
该地区采用分时电价计价方式, 平段时间为7:00—8:00, 11:00—18:00; 谷段时间为23:00—7:00, 峰段时间为8:00—11:00, 18:00—23:00; 具体如表2.
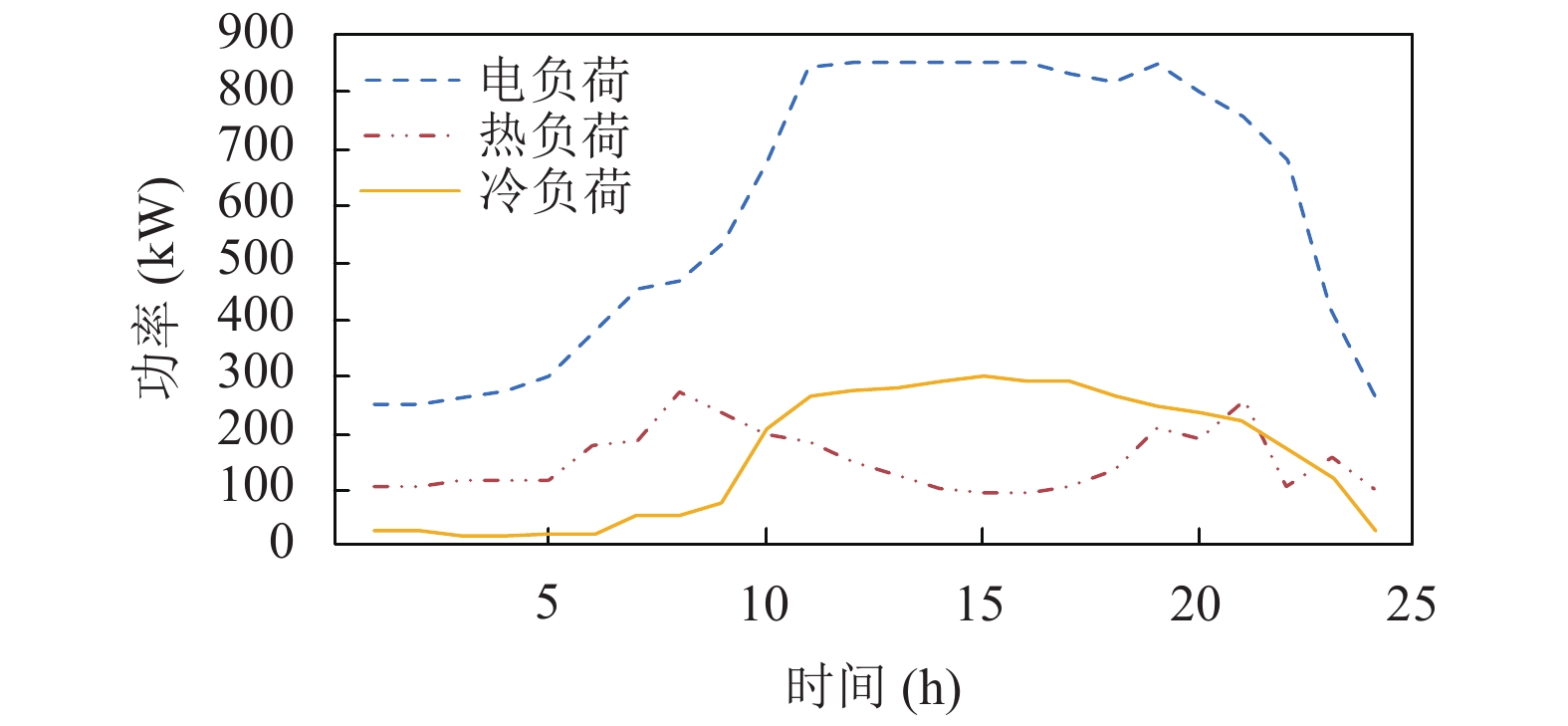
天然气价格为: 3.25元/立方米, 换算为0.33元/kWh. 把各区域的负荷分为电、冷和热负荷. 通过聚类分析以及负荷预测, 获得每个区域的负荷值, 负荷值如图3~图5所示.
根据历史数据预测得到的光伏出力和风电出力的最大值如图6所示.
4.2 算例结果分析场景1. 多源自治运行控制模式.

|
图 3 区域1的冷热电负荷图 |

|
图 4 区域2的冷热电负荷图 |
|
图 5 区域3的冷热电负荷图 |

|
图 6 光伏风电最大出力图 |
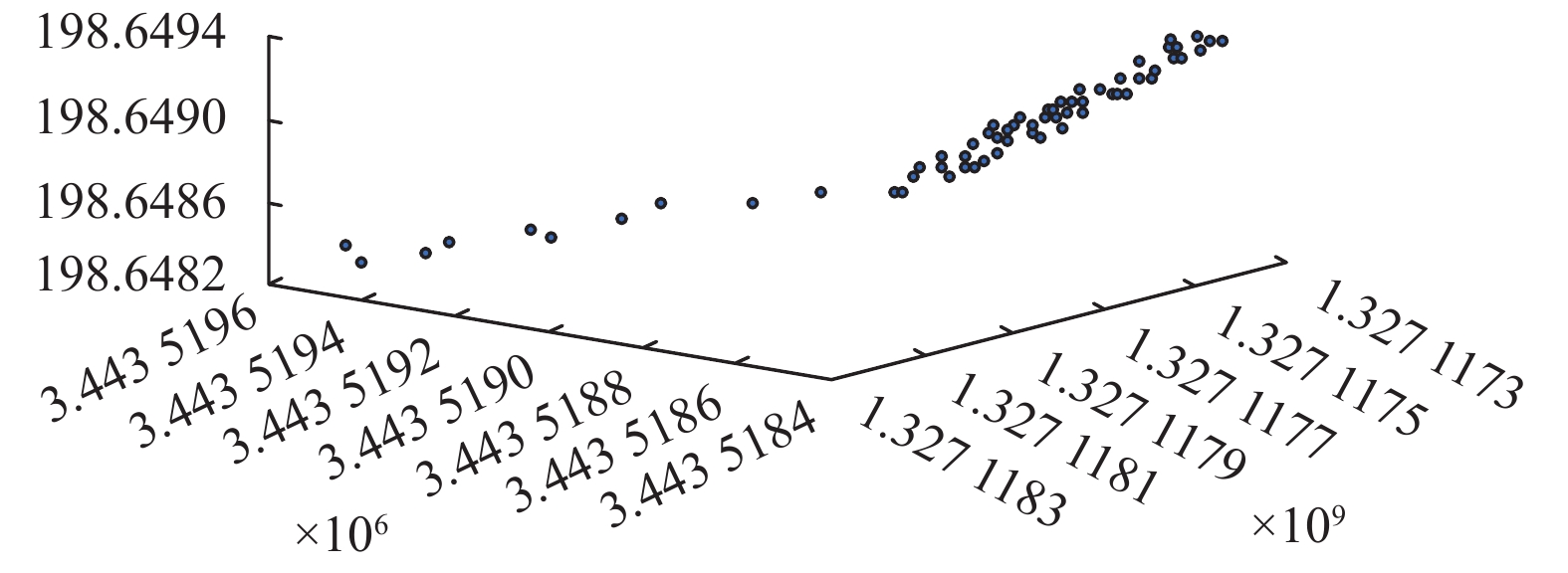
首先, 为了验证基于多智能体的分层分布式协调优化调度的优点, 采用未分层分布式优化调度方式对3个区域进行优化调度, 调度结果如下. 由于本文通过设置多层次多目标进行优化, 因此采用Pareto图来寻找最优解. 各区域的Pareto最优解如图7~图9所示.
|
图 7 区域1的Pareto图 |
各区域的最优解的值如表3所示.
然后, 采用基于多智能体的分层分布式协调优化调度时, 各区域的Pareto最优解如图10~图12所示.
各区域的最优解的值如表4所示.
综合对比最优解值, 未采用基于多智能体的分层分布式协调优化调度时, 总的经济成本为8301元, 燃气耗量为2589 898 J, 新能源的消纳量为8218.6496 kWh, 而采用基于多智能体的分层分布式协调优化调度时, 总的经济成本为8061元, 燃气耗量为2559 898 J, 新能源消纳量为8255.6154 kWh. 因此, 多源自治运行控制模式有良好的优化效果.

|
图 8 区域2的Pareto图 |
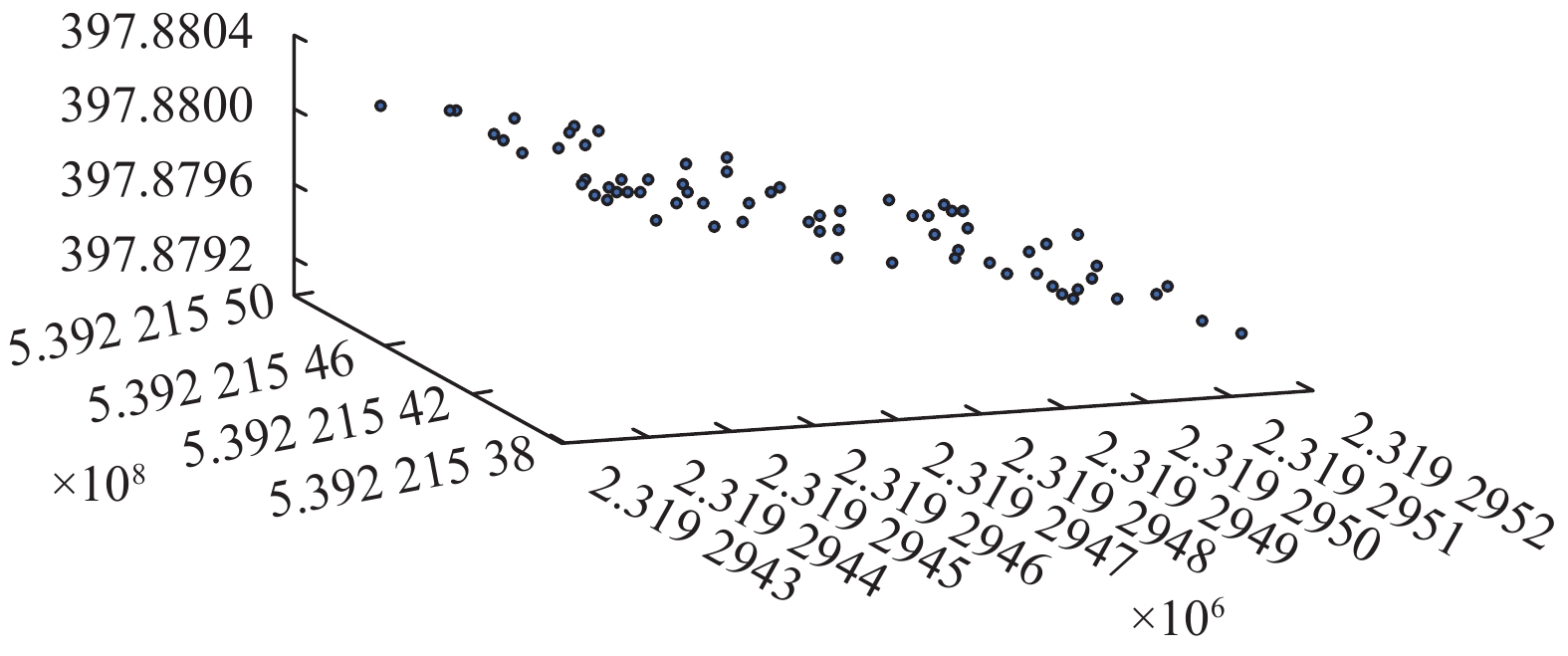
|
图 9 区域3的Pareto图 |
| 表 3 各区域的最优解的值 |

|
图 10 区域1的Pareto图 |

|
图 11 区域2的Pareto图 |

|
图 12 区域3的Pareto图 |
| 表 4 各区域的最优解的值 |
场景2. 多源协同运行控制模式.
全局Pareto最优解如图13.

|
图 13 全局Pareto图 |
各目标的最优解的值及其与场景一对应值的对比如表5.
| 表 5 各目标的最优解的值 |
在多源自治运行控制模式下, 总经济成本为8061元, 燃气耗量为2559 898 J, 新能源消纳量为8255.6154 kWh, 在多源协同运行控制模式下, 总的经济成本为7534元, 燃气耗量为2475 021 J, 新能源消纳量为8337.1667 kWh. 所以, 多源协同运行控制模式比多源自治运行控制模式更优.
因此, 无论是在场景1还是场景2下, 通过分层分布式协调优化调度时, 都有较好的优化效果. 基于全局考虑, 多源协同运行控制模式的优化模式明显能够减少运营成本, 并且提高新能源消纳, 为实现对可调资源的优化利用奠定了基础.
5 结论本文从技术和经济因素层面优化了台区下资源调控及优化的设计模型, 采用分层分布式进行协调优化, 并以模型预测控制作为优化算法进行求解分析. 并通过在场景1: 多源自治运行控制模式下和场景2: 多源协同运行控制模式下进行分析, 得出台区下资源调控及优化的最佳设计模式, 可以通过使用分布式能源发电来提高盈利能力, 同时需要与电网友好互动以提高优化效果. 本研究对制定多源协调优化调度策略、降低电力公司成本、节约资源、减少环境污染, 以及减少社会对电力建设的投入有着重要意义.
| [1] |
张晓静. 浅谈供暖节能新技术及应用. 科技信息, 2012(1): 124. |
| [2] |
崔杨, 张家瑞, 仲悟之, 等. 考虑源-荷多时间尺度协调优化的大规模风电接入多源电力系统调度策略. 电网技术. (2020-02-24).
|
| [3] |
刘敦楠, 李鹏飞, 葛睿, 等. 考虑可调控负荷和储能的区域互联备用优化模型. 电力建设, 2019, 40(12): 22-29. |
| [4] |
何畅, 程杉, 徐建宇, 等. 基于多时间尺度和多源储能的综合能源系统能量协调优化调度. 电力系统及其自动化学报, 2020, 32(2): 77-84, 97. |
| [5] |
徐青山, 王栋, 戴蔚莺, 等. 变频空调负荷虚拟同步机化改造及其参与微网互动调控. 电力自动化设备, 2020, 40(3): 8-14. |
| [6] |
孟显海, 吕红芝, 高辉, 等. 多能互补综合能源优化利用评估技术研究. 电器与能效管理技术, 2019(8): 7-14. |
| [7] |
张跃, 杨汾艳, 曾杰, 等. 主动配电网的分布式电源优化规划方案研究. 电力系统保护与控制, 2015, 43(15): 67-72. |
| [8] |
Gu AL, Zhou XY. Emission reduction effects of the green energy investment projects of China in Belt and Road Initiative countries. Ecosystem Health and Sustainability, 2020, 6(1): 1747947. DOI:10.1080/20964129.2020.1747947 |
| [9] |
Bui N, Castellani AP, Casari P, et al. The Internet of energy: A Web-enabled smart grid system. IEEE Network, 2012, 26(4): 39-45. DOI:10.1109/MNET.2012.6246751 |
| [10] |
黄鹤, 秦岭, 喻洋洋, 等. 水光多能互补清洁能源智能发电技术. 分布式能源, 2020, 5(2): 21-26. |
| [11] |
Lanzisera S, Weber AR, Liao AN, et al. Communicating power supplies: Bringing the Internet to the ubiquitous energy gateways of electronic devices. IEEE Internet of Things Journal, 2014, 1(2): 153-160. DOI:10.1109/JIOT.2014.2307077 |
| [12] |
刘方泽, 牟龙华, 张涛, 等. 微能源网多能源耦合枢纽的模型搭建与优化. 电力系统自动化, 2018, 42(14): 91-98. |
 2020, Vol. 29
2020, Vol. 29



