混合蛙跳算法(Shuffled Frog Leaping Algorithm, SFLA)[1]是Eusuff和Lansey通过模拟青蛙种群的觅食过程而设计出的一种群智能优化算法, 具有概念简单、参数少且全局寻优能力强等优点. 目前, 许多研究学者将其成功应用到不同的工程领域, 雷德明等[2]提出一种新型蛙跳算法(SFLA), 用于求解低碳混合流水车间调度问题, 得到高效率的调度方案. 徐俊等[3]将改进后的混合蛙跳算法(ISFLA)用于求解云工作流调度, 实验证明相同的迭代次数下ISFLA优化的效果更好. 张萍等[4]将人工鱼群与蛙跳算法结合起来改进矢量匹配法, 实现电压传输函数的有理拟合. 陈科尹等[5]提出一种改进的混合蛙跳算法, 有效解决了传统采摘机器人相机标定方法的不足. 蔡宁等[6]提出一种融入Pareto思想的改进混合蛙跳算法(SFLA)用于求解实际资源约束下拆卸线平衡问题, 实验证明改进SFLA具有良好的综合求解优势. 杨哲等[7]将改进实数编码混合蛙跳算法(IR-SFLA)和二进制编码的(IB-SFLA)分别应用到水电站经济负荷分配和机组组合问题, 实验证明IR-SFLA算法能有效提升水资源利用效率, IB-SFLA在求解大规模机组电力调度问题时可获得高质量的解. 张异[8]设计一种求解包装配送问题的混沌蛙跳布谷鸟算法, 实验证明CFLCSA可以得到高效率的配送策略. 艾子义等[9]提出一种新型蛙跳算法(SFLA)用于求解低碳柔性作业车间调度问题, 实验表明新型SFLA具有较强的搜索能力和竞争力. 李荣波等[10]针对标准混合蛙跳算法的不足, 提出一种改进混合蛙跳算法(ISFLA), 来求解梯级水库优化调度问题, 得到了较好的优化结果.
目前, 针对SFLA算法已有了许多先进的研究成果, 但对于离散混合蛙跳算法的理论研究相对较少, 且缺乏相对的实际应用研究. 因此, 本文提出了一种离散混合蛙跳算法(Discrete Shuffled Frog Leaping Algorithm, DSFLA), 在DSFLA算法中引入扰动系数来调控最劣解的跳跃方向, 从而协调迭代过程中算法的全局探索和局部开发能力; 并将扰动系数作为阈值, 引用螺旋更新位置来改进族群内个体的更新策略, 精细算法的局部搜索能力; 同时为了提高算法的全局探索能力, 随机选择种群内的参照个体进行位置更新; 此外采用全局最优解变异提高种群的多样性, 有助于算法跳出局部最优; 最后利用改进的Sigmoid函数对SFLA进行离散化处理保证了个体的多样性. 对改进效果进行仿真验证, 并将DSFLA与其它9种优化算法在求解油田措施规划模型上进行对比, DSFLA取得了很好的寻优效果.
1 离散混合蛙跳算法原理 1.1 基本混合蛙跳算法基本混合蛙跳算法(SFLA)[1]数学模型思想是: 一个湿地里有若干块石头, 青蛙可以在石头上跳跃寻找食物最多的点, 每只青蛙带有不同的信息, 将青蛙种群分为不同的组, 通过不同的青蛙个体进行信息交流, 实现局部搜索, 当局部搜索进行到一定程度时, 混合种群中的各组青蛙, 实现种群内部的信息交换. 根据这一仿生机制, 基本蛙跳算法的寻优过程主要由4部分组成.
(1)种群初始化
在湿地中随机生成N个青蛙组成的初始种群, 其中d维解空间的第i个青蛙表示为
(2)划分族群
通过计算种群内青蛙的适应度值, 根据该值对青蛙进行降序排列; 并将种群划分为m个族群, 每个族群包含n个青蛙, 其中N=m×n.
(3)局部搜索
① 基于局部最优解的族群内个体更新策略
将第
| $ D = rand*({X_{ib}} - {X_{iw}}) $ | (1) |
| $ X'_{iw} = {X_{iw}} + D,\;\;{D_{\min }} \le D \le {D_{\max }} $ | (2) |
② 基于全局最优解的族群内个体更新策略
将种群中适应度最好的解标记为
| $ D = rand*({X_g} - {X_{iw}}) $ | (3) |
| $ X'_{iw} = {X_{iw}} + D,\;\;{D_{\min }} \le D \le {D_{\max }} $ | (4) |
③ 随机生成新个体更新策略
| $ X'_{iw} = rand*{D_{\max }} $ | (5) |
其中,
(4)全局混合
将完成局部搜索后的族群个体重新混合并排序, 再次分组和进行族群内部更新, 直到算法满足结束条件.
1.2 离散混合蛙跳算法原理 1.2.1 族群内个体更新原理改进基本混合蛙跳算法的族群内个体更新策略主要体现在族群内最劣解不断向最优解的位置方向移动. 当迭代到达一定程度后, 族群内最优解和全局最优解难以被更新, 最劣解朝某一固定方向不断跳跃, 易导致算法陷入局部最优. 为了提高算法跳出局部最优的能力, 本文引入扰动系数A来调节个体的跳跃步长, 并将扰动系数A作为概率阈值, 采用标准SFLA族群个体更新位置和螺旋更新位置两种策略来模拟青蛙的觅食行为.
基本混合蛙跳算法的跳跃步长规则如图1所示,可以看出族群中的最劣解
| $ \alpha = 2 - t*((2)/{T_{\max }} $ | (6) |
| $ A = 2\alpha \cdot rand - \alpha $ | (7) |
| $ D = rand*(A*{X_{ib}} - {X_{iw}}),\;\;{D_{\min }} \le D \le {D_{\max }} $ | (8) |
其中, t表示当前迭代次数,
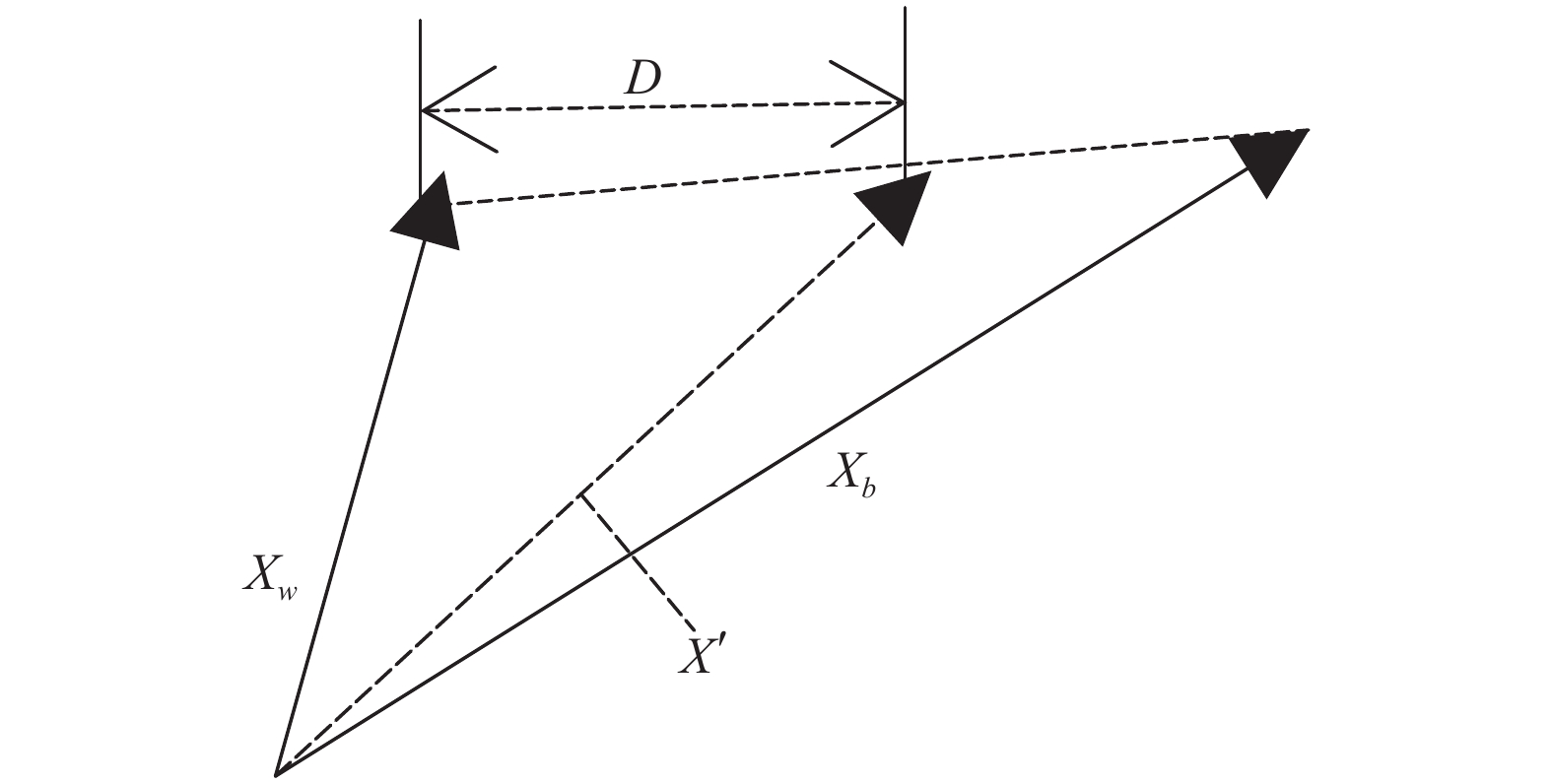
|
图 1 基本跳跃步长规则 |

|
图 2 改进的跳跃步长规则 |
由进化理论可知优秀个体的周围很大程度上存在更多的潜在优秀个体; 基本SFLA算法的迭代后期, 族群内最优解保持不变, 易导致算法陷入局部最优. 为了提高算法的局部搜索能力, 引用螺旋更新位置策略来改进族群内个体的更新方式, 螺旋更新位置策略使最劣解沿着螺旋运动轨迹向最优解的位置方向移动, 螺旋运动方式能对最优解附近区域进行更加全面精细的搜素, 寻找到更多潜在的优秀解. 本文将引入的扰动系数作为阈值, 当
| $ X'_{iw}{\rm{ = }}\left\{ \begin{array}{l} D \cdot {e^{bl}} \cdot \cos (2\pi l) + {X_{ib}},\;\;\left| A \right| \le {\rm{1}} \\ {X_{iw}} + D,\;\;\left| A \right|{\rm{ > 1}} \\ \end{array} \right. $ | (9) |
其中,
在基本混合蛙跳算法迭代过程中, 随机生成新个体的更新策略具有一定的混乱性和无序性, 不利于算法的收敛. 因此本文通过随机选择种群中的一个青蛙个体作为参照青蛙, 以此来寻找其它更优的解. 这样既实现了种群内部信息的充分交流, 同时增强了算法的搜索能力, 使该算法能在全局范围内进行搜索. 其更新公式表达如下:
| $ D = rand*({X_{rand}} - {X_{iw}}) $ | (10) |
| $ X'_{iw} = {X_{iw}} + D,\;\;{D_{\min }} \le D \le {D_{\max }} $ | (11) |
其中,
全局最优解作为重要的信息源会影响整个群体的走势, 但在种群迭代后期, 全局最优解难以被更新, 易导致算法停滞. 因此, 本文借鉴2-opt方法对全局最优解进行变异, 通过让种群内邻域解参与到信息交互中, 从而增加种群的多样性, 有助于算法在迭代后期跳出局部最优. 其更新公式表达如下:
| $ \begin{split} {X_g} = &\left\{ {{x_1},{x_2}, \cdots ,} \right.{x_m},{x_{m + 1}}, \cdots {x_n},{x_{n + 1}}, \cdots ,{x_d}\} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \downarrow \\ {X_g} =& \left\{ {{x_1},{x_2}, \cdots ,} \right.{x_{n + 1}},{x_n}, \cdots ,{x_{m + 1}},{x_m}, \cdots ,{x_d}\} \\ \end{split} $ | (12) |
其中,
根据文献[11]提出的通过计算种群的多样性度量值来评测种群多样性的方法, 在DSFLA算法中引入全局最优解变异策略, 利用式(13)计算的其种群的多样性度量值, 并将结果与标准SFLA算法做对比, 对比结果如图3所示.

|
图 3 种群多样性度量 |
| $ Q(t) = \dfrac{{\displaystyle\sum\limits_{i = 1}^N {\sqrt {\displaystyle\sum\limits_{j = 1}^D {{{(x_{ij}^t - {{\bar X}_j})}^2}} } } }}{{N*{T_{\max }}}} $ | (13) |
其中,
由图3可知, 随着迭代次数的不断增加, DSFLA算法种群多样性度量值逐渐趋向于比SFLA算法较大的一个值, 因此DSFLA 算法的种群性多样性更大.
1.2.4 离散化原理由于实际工程应用中所计算的变量都是离散的, 因此, 本文提出一种离散二进制蛙跳算法编码方式对青蛙位置进行离散化处理. 为了保证迭代过程中青蛙的位置只能取0或1, 通常使用Sigmoid函数[12]将位置压缩到[0, 1]区间, 其公式如式(14)、式(15)所示, 式(14)中的矩阵运算需用到“./”. 利用标准Sigmoid函数对青蛙个体位置映射的结果如图4所示, 可以看出, 映射结果大都集中在0.35~0.65之间, 若直接用标准Sigmoid函数对映射结果离散化处理, 则个体容易产生“靠拢”现象, 会导致算法陷入局部最优, 过早停滞.
| $ s\left( x \right) = 1./(1 + \exp ( - x)) $ | (14) |
| $ x = \left\{ {\begin{array}{*{20}{l}} 1,&{{\rm{rand < }}s(x)}\\ 0,&{{\rm{otherwise}}} \end{array}} \right. $ | (15) |
为了提高算法的搜索能力, 本文通过对最优位置和当前位置的差值进行映射, 同时建立跳跃步长D与位置转换概率间的关系来改进Sigmoid函数; 映射结果如图5所示, 可以看出, 映射结果值分布在0~1之间, 更好的保证了离散化后个体的多样性, 为算法的优化过程奠定了多样性基础. 改进后的Sigmoid函数公式表达如下:
| $ x = 2*rand(VarSize).*({x_g} - x) $ | (16) |
| $ s(x) = \left| {2./(1 + \exp ( - x)) - 1} \right| $ | (17) |
| $ x = \left\{ \begin{array}{l} 1,\;\;D \ge 0,rand \le s(x) \\ 0,\;\;D < 0,rand \le - s(x) \\ \end{array} \right. $ | (18) |
其中,
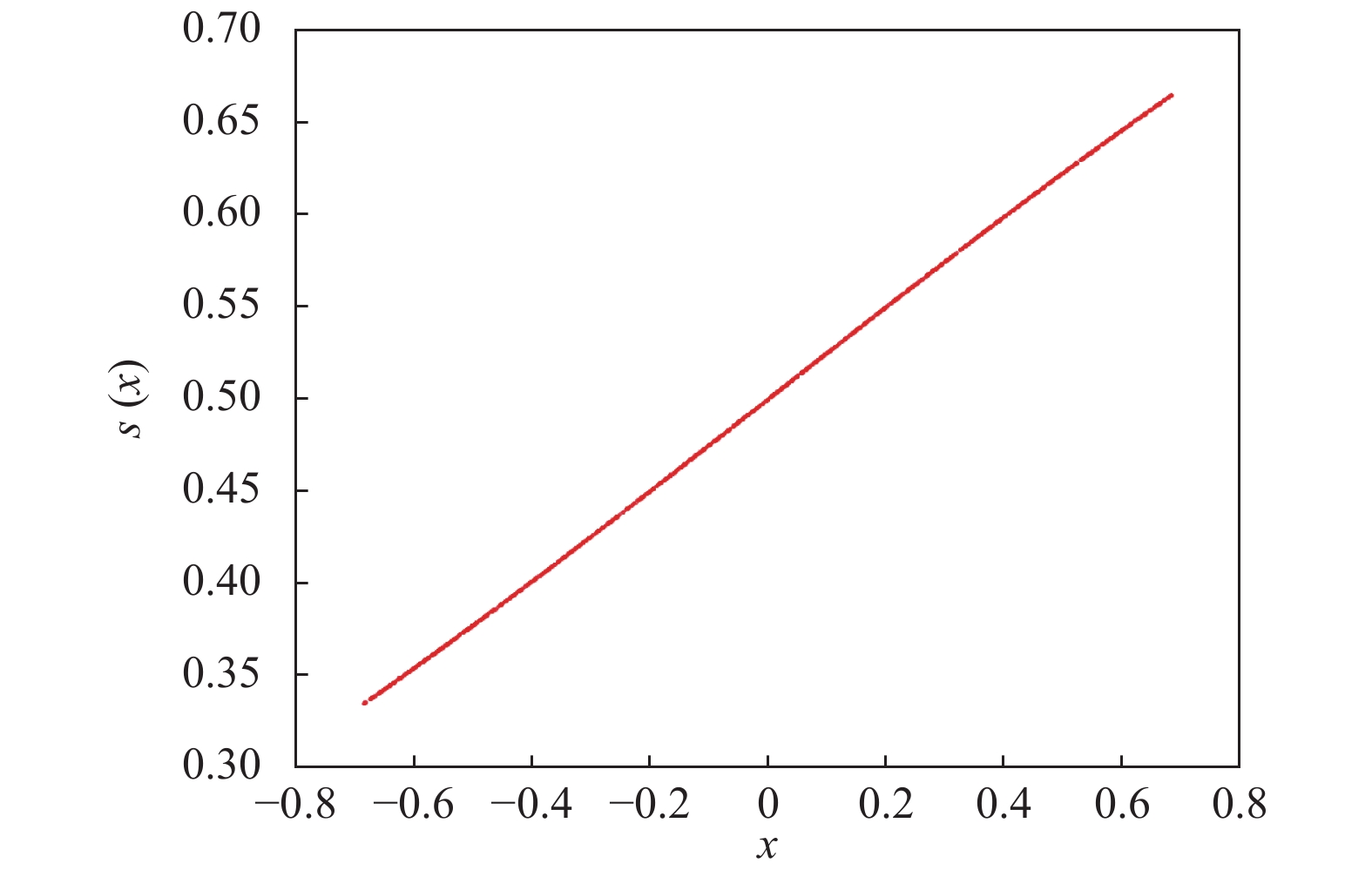
|
图 4 标准Sigmoid函数 |

|
图 5 改进Sigmoid函数 |
1.3 离散混合蛙跳算法
离散混合蛙跳算法(DSFLA)的具体操作步骤如算法1所示.
算法1. 离散混合蛙跳算法
1. 初始化参数(种群规模N, 族群数m, 维数D, 局部搜索次数L, 最大迭代次数Tmax);
2. 随机生成初始青蛙种群;
3.
4. 应用式(6)、式(7)更新参数
5.
6.
7. 计算第i个族群的局部最优解xib, 局部最劣解xiw, 全局最优解xg;
8.
9. 应用式(6)~式(9)得到新的
10.
11 应用式(6)~式(9)得到新的
12.
13. 应用式(15)~式(17)对更新后的个体
14.
15.
16.
17. 应用式(3)、式(4)得到新的
18. 应用式(15)~式(17)对更新后的个体
19.
20.
21.
22. 应用式(10)、式(11)得到新的
23. 应用式(15)~式(17)对更新后的个体
24.
25.
26.
27.
28.
29. 应用式(12)对全局最优解
30.
31
32.
33.
34.
本文选用了9个常用的基准测试函数[13]如表1所示. 将离散混合蛙跳算法(DSFLA), 同基本混合蛙跳算法(SFLA)[1], 鲸鱼优化算法(WOA)[14], 灰狼算法(GWO)[15], 飞蛾扑火算法(MFO)[16], 布谷鸟算法(CSA)[17], 蝙蝠算法(BAT)[18], 多元宇宙算法(MVO)[19], 粒子群算法(PSO)[20], 乌贼算法(CFA)[21] 9种优化算法进行实验对比. 参数设置如表2所示, 最大迭代次数为100, 种群数为60, 重复10次, 采用平均值(mean), 标准差值(std)以及迭代中的最优值(best)来评价算法的性能.
| 表 1 基准测试函数 |
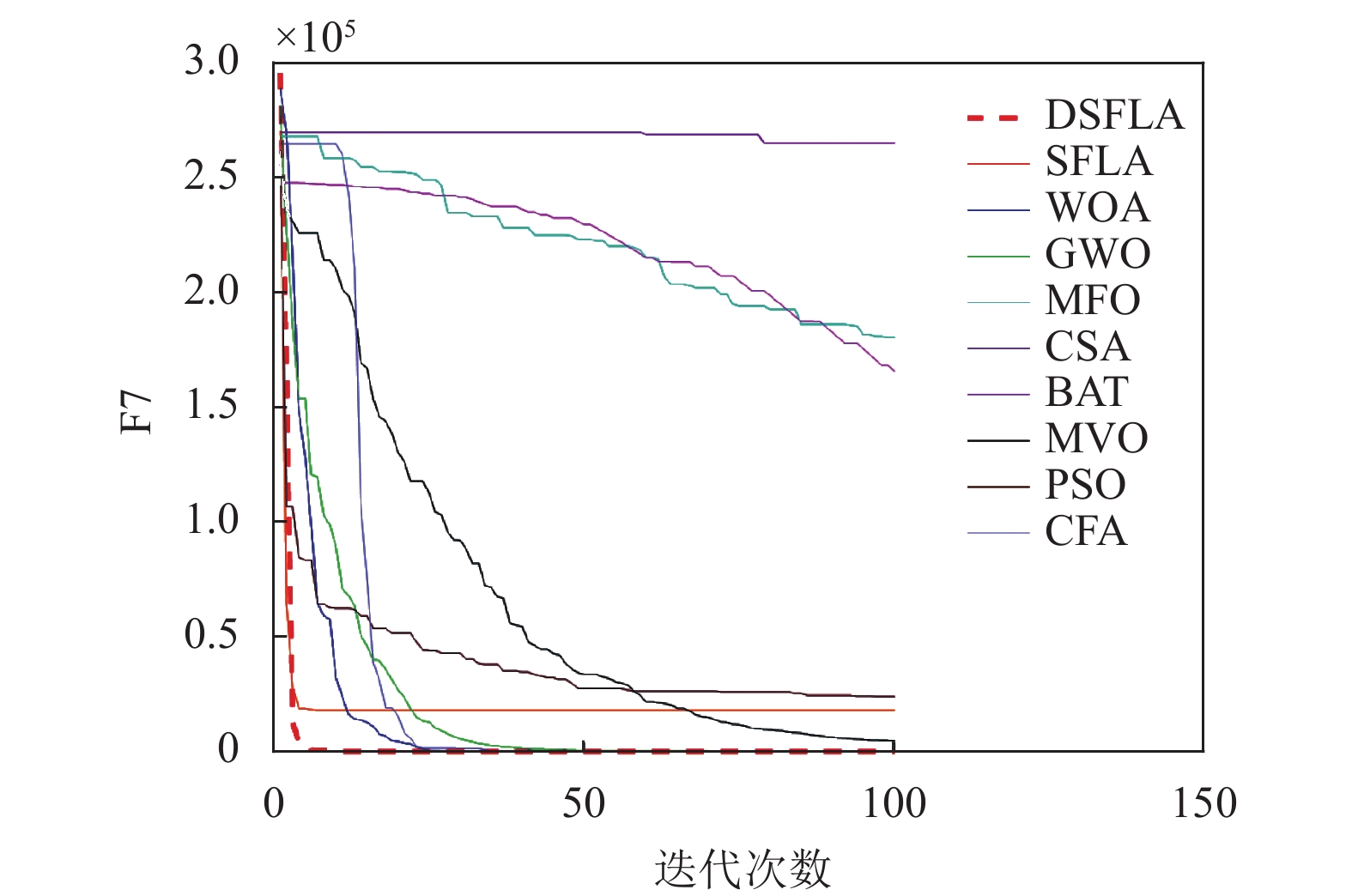
表3为10种优化算法在9个测试函数中的实验结果对比. 图6~图14为对应的迭代图. 以最优值和平均值为评判标准, 通过比较10种算法的优化结果可知, 在函数参数条件设定相同的情况下, DSFLA寻优结果最好. 上述实验结果主要原因是DSFLA引入扰动系数更新策略来随机选取族群最优解的位置作为最劣解的跳跃方向, 可以更好的平衡算法在不同迭代时期的全局搜索和局部开发能力, 使青蛙可以更快的靠近食物; 同时将扰动系数作为阈值, 引用螺旋更新位置来改进族群内个体更新策略, 对最优解位置附近进行精细搜索, 使青蛙能够更准确的找到食物的位置, 从而提高了算法局部搜索的精度.
以方差为评判标准, DSFLA的收敛精度和方差都较优于其它9种算法. 实验结果主要原因是在迭代过程中, 其它个体会逐渐集中在最优个体的位置附近, 导致算法过早停滞; DSFLA算法通过全局最优解变异的方式增加种群的多样性, 避免青蛙个体全部聚集在某个局部最优位置; 同时采用随机搜索策略, 提高算法的全局搜索能力.
综上所述, 针对标准混合蛙跳算法在求解高维复杂函数时存在收敛精度低和寻优速度慢等问题, 本文采用的改进的策略能够明显提高了DSFLA算法的收敛速度和寻优性能.
| 表 2 算法参数设置 |
| 表 3 实验结果对比表 |

|
图 6 F1迭代图 |

|
图 7 F2迭代图 |
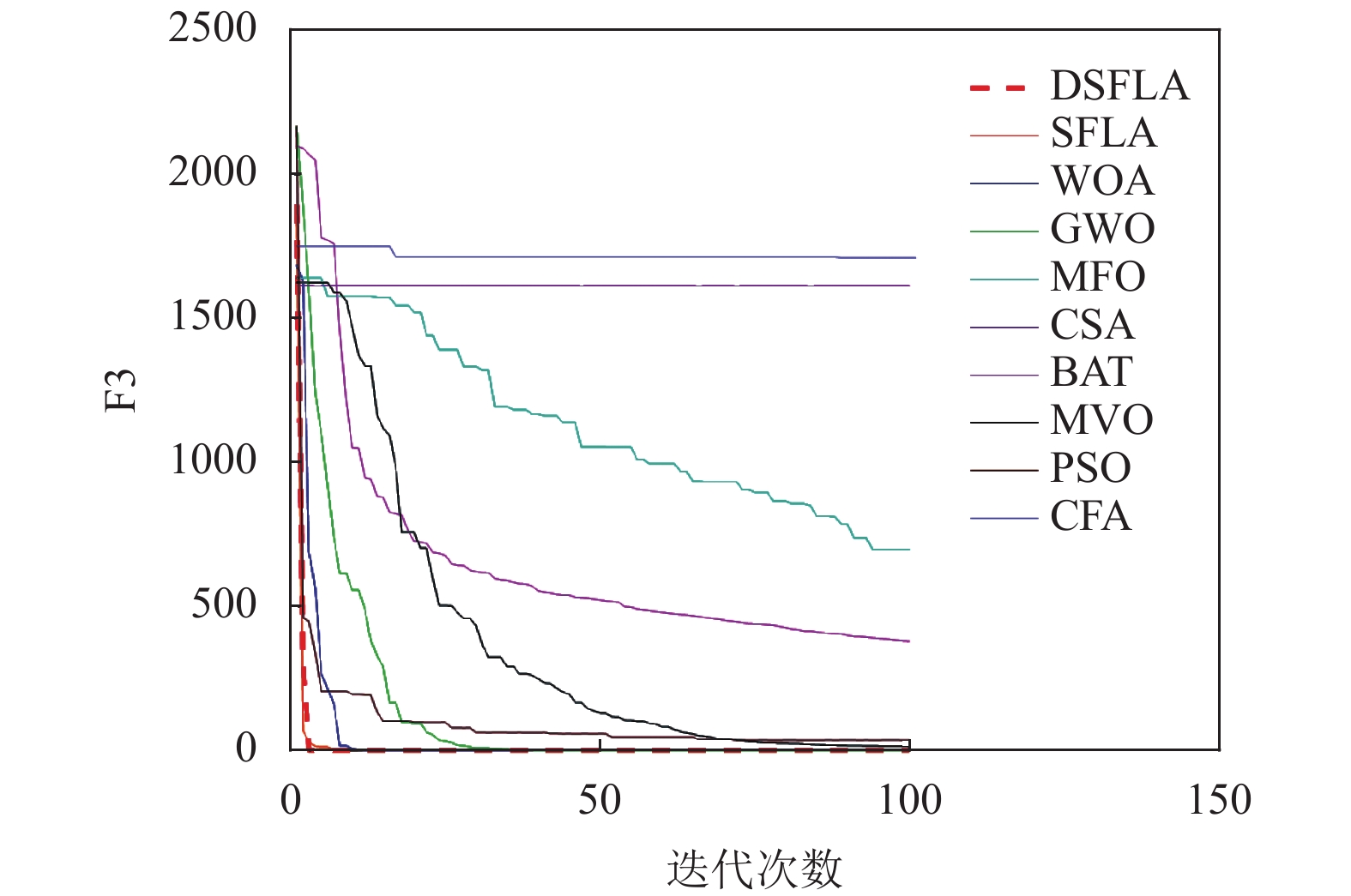
|
图 8 F3迭代图 |

|
图 9 F4迭代图 |
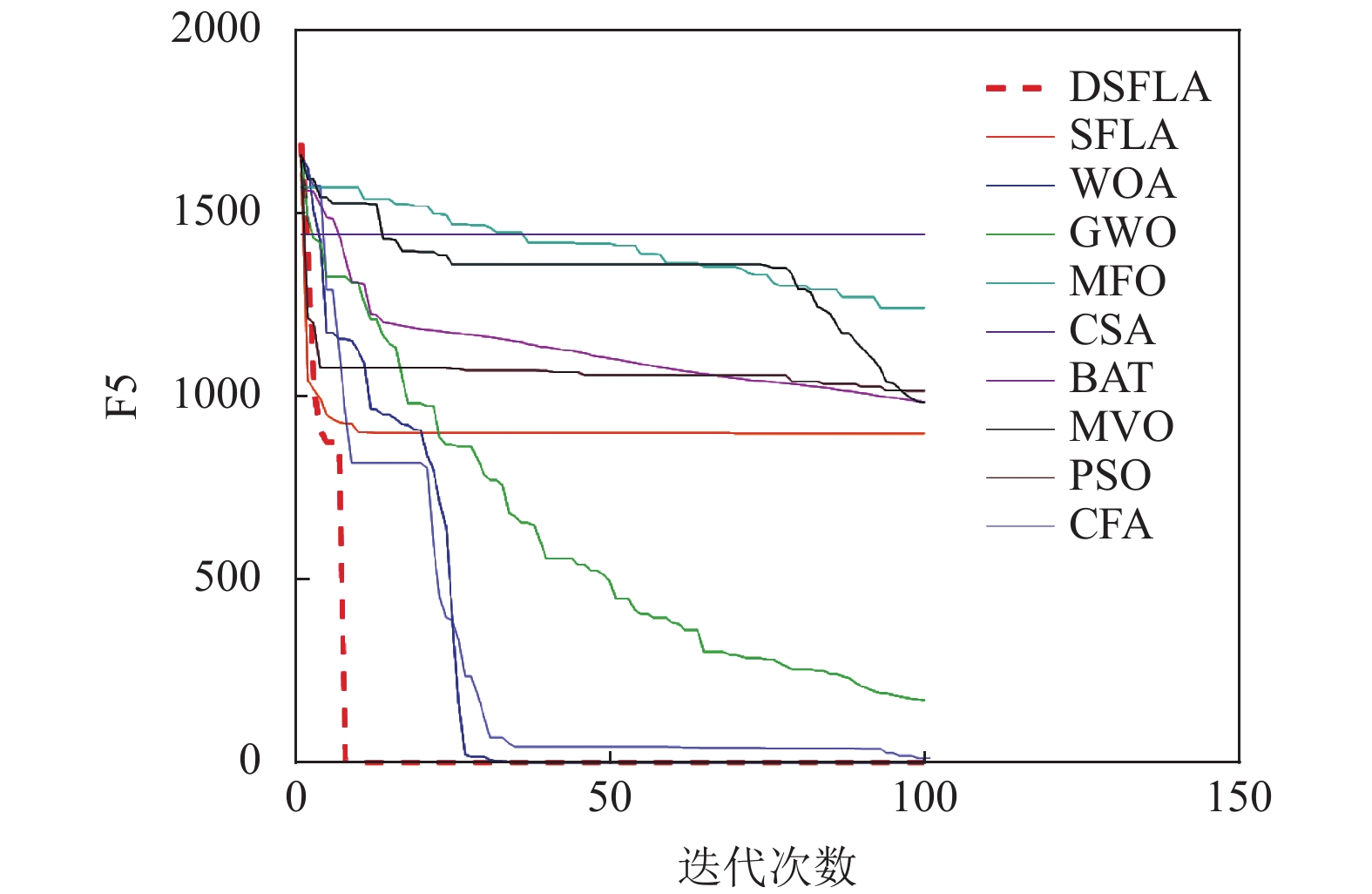
|
图 10 F5迭代图 |

|
图 11 F6迭代图 |
|
图 12 F7迭代图 |

|
图 13 F8迭代图 |

|
图 14 F9迭代图 |
3 基于DSFLA的油田措施方案优化
本文以年度利润和累积利润投入比最大为目标函数, 建立油田措施规划模型, 通过和其它9种算法优化结果进行对比, 分析DSFLA在优化油田措施规划中的性能.
3.1 实验油田措施规划数学模型(1)目标函数
油田措施规划问题是在满足油田开采的约束条件的前提下, 分配开采井组, 使油田的年度利润和累积利润投入比最大, 其目标函数如下:
| $ \max \;\;{F_1} =\frac{{\displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{j = 1}^K {{e^{ - dt}}*(x{{\rm{1}}_{ij}} \!+\! y{{\rm{1}}_{ij}})*a \!-\! \displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{j = 1}^K {{\textit{z}}{{\rm{1}}_{ij}}*b \!-\! } } } } \displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{j = 1}^K {w{{\rm{1}}_{ij}}*c} } }}{{\displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{j = 1}^K {{e^{ - dt}}*(x{{\rm{1}}_{ij}}*pric{e_{ij}} + } } y{{\rm{1}}_{ij}}*pric{e_{ij}})}} $ | (19) |
| $ \max \;\;{F_{\rm{2}}} =\frac{{\displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{j = 1}^K {{e^{ - dt}}*(x{{\rm{2}}_{ij}} \!+\! y{{\rm{2}}_{ij}})*a \!-\! \displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{j = 1}^K {{\textit{z}}{{\rm{2}}_{ij}}*b \!-\! } } } } \displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{j = 1}^K {w{{\rm{2}}_{ij}}*c} } }}{{\displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{j = 1}^K {{e^{ - dt}}*(x{{\rm{2}}_{ij}}*pric{e_{ij}} + } } y{{\rm{2}}_{ij}}*pric{e_{ij}})}} $ | (20) |
式中,
(2)约束条件
1)措施增油量约束
| $ \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {{e^{ - dt}}*x{{\rm{1}}_{ij}} = {t_o}} } $ | (21) |
| $ 0 \le \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {{e^{ - dt}}*y{{\rm{1}}_{ij}} - {t_e} \le {t_e}*\partial } } $ | (22) |
式中,
2)措施增液量和增注量约束
| $ \left| {{t_l} - \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {{\textit{z}}{{\rm{1}}_{ij}}} } } \right| \le {t_l}*\partial $ | (23) |
| $ \left| {{t_i} - \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {w{{\rm{1}}_{ij}}} } } \right| \le {t_i}*\partial $ | (24) |
式中,
3)措施数上限约束
| $ 0 \le \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {{K_{ij}} \le Limi{t_{ij}}} } $ | (25) |
式中,
为验证所提算法在求解油田措施规划模型中的性能, 本章采用10种优化算法针对2490口措施井进行方案分配. 算法的参数设置如表1所示, 最大迭代次数为1000, 种群大小为100, 实验结果如图15, 图16所示. 图15, 图16表示的是10种优化算法迭代情况图. 表4, 表5表示10种优化算法得到的最优值、最差值、平均值和标准差.

|
图 15 年度利润对比图 |

|
图 16 累积利润对比图 |
| 表 4 年度利润F1算法结果对比 |
| 表 5 累积利润F2算法结果对比 |
由表4和表5的实验结果可知, 从最优值、最差值方面来看, DSFLA得到的优化结果最好. 在迭代过程中, DSFLA算法引入扰动系数更新策略, 更好的调控族群内最劣解和最优解之间的距离; 并将扰动系数作为阈值, 使用基于族群最优解的个体更新位置和螺旋更新位置两种策略, 精细算法的局部搜索能力; 此外, 为了增加种群多样性, 采用全局最优解变异的方式; 同时, 采用随机搜索策略来提高算法的全局搜索能力; 为了保证离散化处理后青蛙种群的多样性, 采用改进的Sigmoid函数离散化位置向量, 避免种群的多样性不会在离散化处理后突然骤减, 提高了算法跳出局部最优的能力.
从标准差和平均值方面可知, DSFLA算法相较于其它算法有较好的稳定性. 此外, 从图15和图16中可知, 相较于其它算法, CSA算法最早陷入局部最优, BAT、GWO、MFO、WOA和PSO算法在600代左右停滞, SFLA算法在700代以后也不再变化, 而DSFLA算法的收敛曲线在700以后仍有上升的趋势, 由于最优解变异和随机搜索策略提高了DSFLA在迭代后期跳出局部最优能力, 并且扰动系数更新策略扩大DSFLA算法的搜索空间, 因此同其他9种算法相比, DSFLA可以得到高质量的解.
综上所述, DSFLA算法在求解油田措施规划模型时, 能够显著提升油田开采的经济效益.
4 结论与展望本文提出一种离散混合蛙跳算法(DSFLA), 该算法引入扰动系数、螺旋位置更新策略、随机搜索策略以及全局最优解变异策略来对标准混合蛙跳算法的更新策略进行改进, 此外,为了让改进的算法更适合求解离散优化问题, 利用改进的Sigmoid函数对位置进行离散化处理. 通过9个基准测试函数的实验结果表明了改进策略的高效性, 并成功的将其应用到油田措施规划模型优化问题中, 结果表明, 与其它9种算法的优化结果相比, DSFLA算法求解质量更优. 今后将进一步研究本算法在其它工程领域的应用.
| [1] |
Eusuff MM, Lansey KE. Optimization of water distribution network design using the shuffled frog leaping algorithm. Journal of Water Resources Planning and Management, 2003, 129(3): 210-225. |
| [2] |
雷德明, 杨冬婧. 基于新型蛙跳算法的低碳混合流水车间调度. 控制与决策, 2019, 35(6): 1329-1337. |
| [3] |
徐俊, 项倩红, 肖刚. 基于改进混合蛙跳算法的云工作流负载均衡调度优化. 计算机科学, 2019, 46(11): 315-322. DOI:10.11896/jsjkx.181001866 |
| [4] |
张萍, 李婷, 张宏伟, 等. 基于人工鱼群和蛙跳混合算法的特高压电力变压器的建模研究. 电瓷避雷器, 2018(6): 7-12, 19. |
| [5] |
陈科尹, 邹湘军, 关卓怀, 等. 基于混合蛙跳优化的采摘机器人相机标定方法. 农业机械学报, 2019, 50(1): 23-34. DOI:10.6041/j.issn.1000-1298.2019.01.002 |
| [6] |
蔡宁, 张则强, 张颖, 等. 资源约束下拆卸线平衡问题的建模与改进混合蛙跳算法. 中国机械工程, 2019, 30(17): 2091-2099. DOI:10.3969/j.issn.1004-132X.2019.17.011 |
| [7] |
杨哲, 杨侃, 吴云, 等. 改进二进制-实数编码混合蛙跳算法在水电机组短期发电调度中的应用. 天津大学学报(自然科学与工程技术版), 2019, 52(9): 979-989. |
| [8] |
张异. 基于包装配送问题的混沌蛙跳布谷鸟算法研究. 包装工程, 2019, 40(5): 174-179. |
| [9] |
艾子义, 雷德明. 基于新型蛙跳算法的低碳柔性作业车间调度. 控制理论与应用, 2017, 34(10): 1361-1368. DOI:10.7641/CTA.2017.60768 |
| [10] |
李荣波, 纪昌明, 孙平, 等. 基于改进混合蛙跳算法的梯级水库优化调度. 长江科学院院报, 2018, 35(6): 30-35. |
| [11] |
韩超, 段纬然, 贾长治, 等. 基于改进多种群PSO算法的火炮随动系统调节器参数优化. 火力与指挥控制, 2020, 45(6): 56-61, 66. |
| [12] |
Saremi S, Mirjalili S, Lewis A. How important is a transfer function in discrete heuristic algorithms. Neural Computing and Applications, 2015, 26(3): 625-640. |
| [13] |
龚文引. 差分演化算法的改进及其在聚类分析中的应用研究[博士学位论文]. 武汉: 中国地质大学(武汉), 2010.
|
| [14] |
Mirjalili S, Lewis A. The whale optimization algorithm. Advances in Engineering Software, 2016, 95: 51-67. |
| [15] |
Kennedy J, Eberhart R. Particle swarm optimization. Proceedings of International Conference on Neural Networks (ICNN’95). Perth, Australia. 1995. 1942–1948.
|
| [16] |
Mirjalili S, Mirjalili SM, Hatamlou A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Computing and Applications, 2016, 27(2): 495-513. |
| [17] |
Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Advances in Engineering Software, 2014, 69: 46-61. |
| [18] |
Mirjalili S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowledge-Based Systems, 2015, 89: 228-249. |
| [19] |
Yang XS, Deb S. Cuckoo search via Lévy flights. Proceedings of 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC). Coimbatore, India. 2009. 210–214.
|
| [20] |
Yang XS. A new metaheuristic bat-inspired algorithm. In: González JR, Pelta DA, Cruz C, et al, eds. Nature Inspired Cooperative Strategies for Optimization (NICSO 2010). Berlin: Springer, 2010. 65–74.
|
| [21] |
Eesa AS, Brifcani AMA, Orman Z. Cuttlefish algorithm–A novel bio-inspired optimization algorithm. International Journal of Scientific & Engineering Research, 2013, 4(9): 1978-1986. |
 2020, Vol. 29
2020, Vol. 29



