随着人工智能技术的发展, 燃气公司的智能化成为全球燃气行业关注的焦点. 天然气负荷预测的结果是燃气集团对燃气系统进行决策的依据. 燃气负荷预测可用于燃气系统的生产调度和安全评估. 准确的预测结果有助于提高燃气系统的效率, 降低运营成本, 促进整个燃气行业健康地发展. 国内外许多研究学者都在燃气负荷预测领域投入大量的精力[1]. 美国能源信息署(EIA)预测了美国长期的天然气资源需求, 发现美国的天然气需求在2035年将达到7518亿立方米, 年需求量将增加0.7%. 因此天然气作为清洁能源, 其准确的预测对于燃气系统的健康发展具有重要的意义.
在过去的二十年中, 燃气负荷的常用方法主要有时间序列模型、线性回归模型、SVM和神经网络模型. 但是, 与单模型方法相比, 组合模型可以更好地发挥各个模型的优势, 规避缺点, 在解决复杂的非线性问题中展现了更高的可靠性和准确性[2].
燃气负荷预测的难点在于具有燃气变化趋势具有较大的复杂性和特征因子具有较大的冗余性.
集合经验模态分解法 (Ensemble Empirical Mode Decomposition, EEMD) 是针对传统 EMD 在处理非平稳的时间序列信号时会出现模态混叠的情况而提出的改进算法, 将离散无序信号分解成不同频率的相互独立平稳的特征模态函数[3]. 剥离出来的有限本征模函数IMF分量代表了原始信号不同时间尺度的特征, 这非常适合复杂的, 非平稳、非线性的时间序列数据[4]. 邓带雨等[5]在预测电力负荷的时候通过集合经验模态分解将电力负荷数据分解为频率由高到低的不同本征模态函数, 可以预测随机性较强的局部特征. 王晓霞等[6]通过EEMD算法将非平稳非线性的负荷序列分解后进行预测, 预测精度有了明显的提高. 总之, IMF函数具有与采样频率相关的特点可以摆脱傅里叶变换的局限性, 很好地捕捉负荷数据内部特性, 降低负荷数据的复杂性.
天然气负荷受多种因素影响, 当全面收集这些数据难免包含了大量的冗余信息, 这会提高过拟合的风险, 降低预测准确性. 在能源预测领域中, 主成分分析(Principal Component Analysis, PCA)可以删除数据冗余特征, 可以大大地提升预测精度[7]. Bianchi等[8]使用PCA进行数据降维, 再将数据放入回声状态网络进行罗马电力短期负荷的预测. 在与单一的ESN的比较中, PCA-ESN的误差减少了7.34%. 但是在传统的PCA中只考虑特征与特征之间的相关性而摒弃了特征与预测标签的相关性, 即PCA算法在选取主成分个数的时候, 仅仅考虑了原始数据的方差贡献率, 没有考虑到主成分与预测标签的相关性, 这可能在降维过程中丢失与预测标签更为相关的特征, 导致次要信息的丢失. 为了解决这一问题, 文献[9]在主成分分析的基础上加入相关性分析, 以皮尔逊相关系数为指标, 选取了与燃气负荷值皮尔逊相关系数更高的主成分作为模型的输入, 既去除了特征与特征之间的相关性, 又筛选出与预测标签更为相关的特征. 但是, 皮尔逊相关系数仅仅只能计算特征与预测标签的线性关系, 然而燃气负荷预测据有非线性的特点[10], 所以皮尔逊相关系数不能很好地作为衡量特征与负荷标签的关系. 互信息可以测量随机变量之间的任意函数关系. 针对上述问题, 本文在主成分分析中加入了互信息(Mutual Information, MI)分析, 使用互信息代替皮尔逊相关系数作为评价主成分和预测标签的指标, 可以更好的捕捉到主成分和预测标签的任意函数关系.
在燃气负荷领域中, 神经网络模型目前的应用最为广泛, 其中典型的BP神经网络、RBF神经网络都取得了不错的效果. 但是, 这些神经网络存在一个缺点, 它们不能保存上个时刻的信息, 由于燃气负荷受历史负荷的影响较大, 所以这种类型的网络在处理时间序列预测问题还使存在着一定的局限性. 对于上述浅层结构的神经网络对于复杂的燃气负荷预测出现的问题, 文献[11]分析了浅层神经网络在时间序列分析预测的不足. 随着深度学习的发展, 深层次的神经网络在复杂的问题面前具有更好的泛化能力. LSTM 算法是 1997 年被提出, 用于语言处理方面的研究, LSTM存在一个记忆单元可以存储之前时刻的计算信息, 使LSTM可以在多维度时间序列的预测问题中得到了较好的实验结果[12], 所以本文使用LSTM神经网络作为燃气短期负荷预测模型, 证明LSTM在燃气负荷预测的有效性.
综上所述, 本文提出了一种新型的组合模型, 主要通过EEMD、MIPCA和LSTM进行组合进行燃气负荷的日预测. 该模型采用EEMD将复杂的燃气负荷序列分解为简单的IMF分量, 并通过MIPCA进行特征的降维, 避免了特征之间冗余性的问题, 使用LSTM模型产生最后的预测结果. 本文首次通过将 EEMD 算法、MIPCA和 LSTM 神经网络组合进行对燃气负荷数据的预测, 使得 LSTM 模型更能把握历史负荷数据的内在规律, 提高预测的精度.
1 研究方法 1.1 EEMD集合经验模态分解法 (Ensemble Empirical Mode Decomposition, EEMD)是一种自适应信号时频分解方法, 它针对传统 EMD 在处理间歇性的时间序列信号时容易出现模式混淆情况而提出的改进算法[13]. 由于自身对数字信号处理的强大优势, 在能源预测领域的具有高可靠性. EEMD在EMD的基础上加入了白噪声辅助信号的处理, 将真实时间序列和白噪声进行混合, 分解后的 IMF 分量应满足近似为周期函数并包含了原信号的不同时间尺度的局部特征信号. EEMD 的处理流程如下:
Step 1. 在原始时间序列x(t)多次添加随机的白噪声序列, 得到复合的时间序列数据xi(t).
| ${x^i}(t) = x(t) + {o^i}(t),\;i = 1,2,3,\cdots,n$ | (1) |
Step 2. 使用EMD算法将加入白噪声的信号分解为各IMF分量.
| ${x^i}(t) = \sum\nolimits_{i = 1}^n {{c_i}(t) + {r_n}(t)} $ | (2) |
其中, n为EMD分解的阶数,
Step 3. 重复Step 1和Step 2, 每次加入不同的随机白噪声序列, 最终得到多组IMF分量集合.
Step 4. 对IMF分量集合进行平均得到最终EEMD信号分解结果.
| ${c_n}(t) = \frac{1}{N}\sum\limits_{i = 1}^n {{c_{i,n}}(t)} $ | (3) |
| ${r_m}(t) = \frac{1}{N}\sum\limits_{i = 1}^n {{r_{i,m}}(t)} $ | (4) |
最终的分解结果为:
| $x(t) = \sum\limits_{i = 1}^m {{c_n}(t) + {r_m}(t)} $ | (5) |
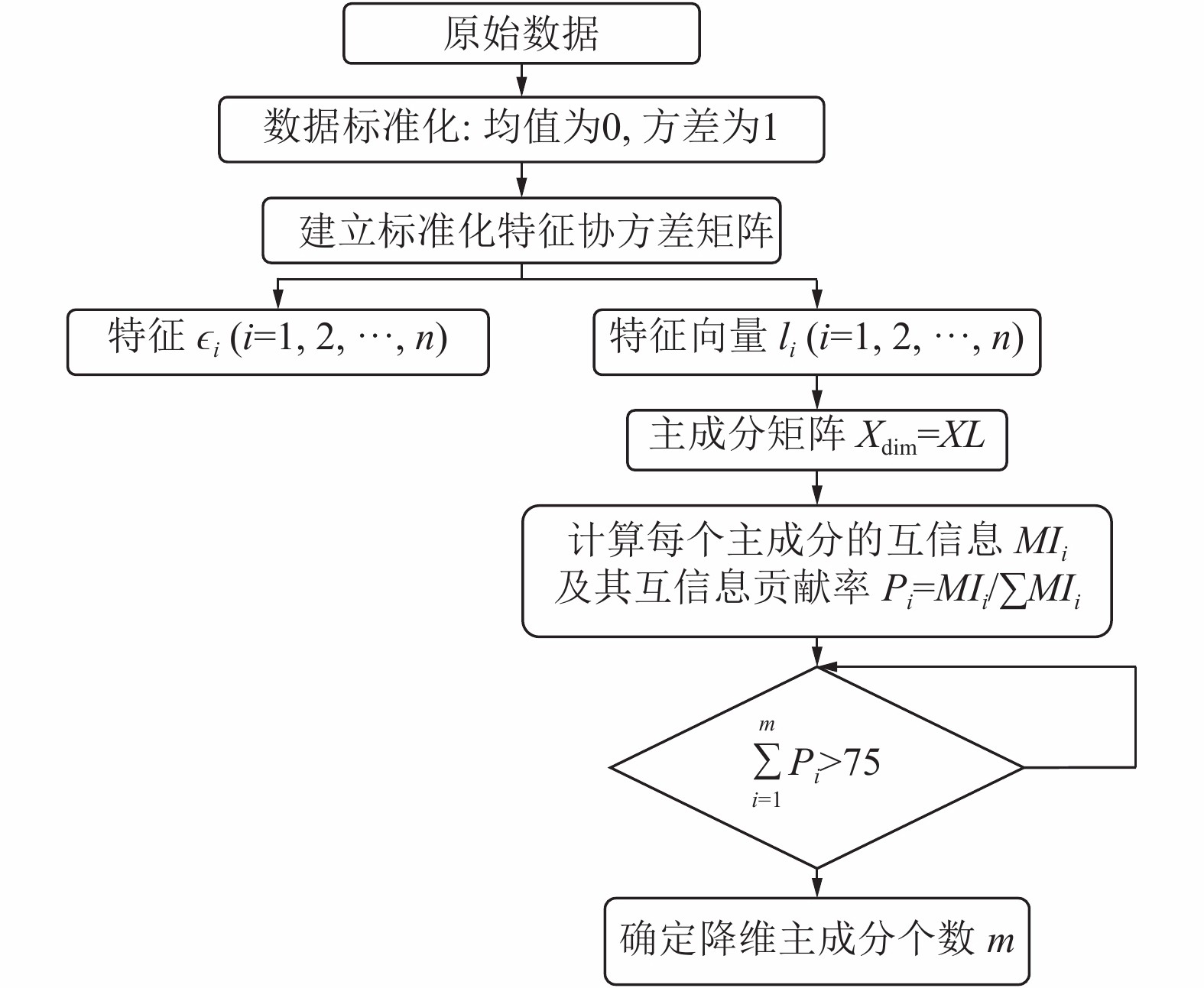
在主成分分析过程中加入了互信息分析, 充分考虑特征与预测标签的关系. 互信息主成分分析法通过结合互信息分析和协方差方法, 可以自动的在原始数据中提取与燃气负荷更为相关的特征, 是一种有效的数据预处理技术. 主要分为4个步骤:
Step 1. 数据标准化, 在大型数据分析项目中, 数据的量纲和来源不同, 为了使数据有更好的可比性, 需要对数据进行标准化处理.
| $x_{\rm stand}^i = \frac{{{x^i} - x_{\rm mean}^i}}{{x_{\rm std}^i}}$ | (6) |
其中, i=1, 2, ···, n为原始数据的特征个数,
Step 2. 计算特征之间的协方差矩阵, 通过矩阵的特征分解, 计算协方差矩阵的特征值向量
| $ c = \frac{1}{m}{x^{\rm T}}x $ | (7) |
Step 3. 使用式(8)计算出每个主成分与燃气负荷的互信息
于阈值的时候, n就作为主成分的个数, 本文选择75%作为阈值. 互信息PCA整体流程如图1所示.
| $I(m;y) = H(Y) - H(Y|m) = \sum\limits_{y \in Y}^{} {\sum\limits_{{m_i} \in X}^{} {P(m,y)\log (\frac{{P(m,y)}}{{P(m)P(y)}})} } $ | (8) |
|
图 1 MICPA流程图 |
1.3 LSTM
长短期记忆网络(LSTM)因为含有特殊的记忆单元, 可以更好地保存过去时刻中数据的信息. LSTM是RNN的一种完善, 解决RNN中容易出现梯度消失的问题. LSTM与其他神经网络的最主要的区别是隐藏层的神经元并不是相互独立的, 隐藏层神经元不仅要接收这个时刻的输入还要接受之前时刻的时序输入. 这个特点可以很好处理与时间序列预测等相关问题.
LSTM单元结构如图2所示. LSTM单元内存在cell存储当前LSTM单元的内部状态. LSTM单元存在3个控制门, 分别是遗忘门、输出门和输入门. 遗忘门(forget gate) 用来控制上一单元状态的被遗忘程度.
| ${f_t} = \sigma ({W_f}*[{h_{t - 1}},{X_t}] + {b_f})$ | (9) |
式中,

|
图 2 LSTM单元结构 |
输入门对当前输入的信息保存在记忆单元的新信息量, 并于过去时间节点的信息进行结合.
| ${i_t} = \sigma ({W_t}*[{h_{t - 1}},{X_t}] + {b_i})$ | (10) |
| $ {C}_{t}^{\sim}={\rm tanh}({W}_{c}*\left[{h}_{t-1},{X}_{t}\right]+{b}_{c}) $ | (11) |
| ${C_t} = {f_t}*{C_{t - 1}} + {i_t}*C_t^\sim$ | (12) |
输出门产生下一时刻传递到神经元的信号量.
| ${h_t} = \sigma ({W_o}*[{h_{t - 1}},{X_t}] + {b_o})*\tanh {C_t}$ | (13) |
使用EEMD-MIPCA-LSTM模型用于短期燃气负荷预测. 该模型采用EEMD将复杂的燃气负荷序列分解为简单的IMF分量, 并通过MIPCA进行特征的降维, 避免了特征之间冗余性的问题, 使用LSTM模型产生最后的预测结果. 具体流程入图3所示.

|
图 3 燃气预测流程 |
2 实验对比
为了验证本文方法的可行性, 使用了上海吴淞地区2005年到2014年共3114天的日燃气负荷数据, 燃气负荷值如图4所示. 数据的特征包括天气类型(平均温度、温差、加热系数和天气状况)和日期类型(星期几、季度、月份). 数据集中2749条数据作为训练集进行模型的训练、365条数据作为测试集.

|
图 4 上海吴淞地区燃气负荷值 |
2.1 基于互信息主成分分析的LSTM模型
为了在降维过程中考虑特征对燃气负荷的影响, 采用互信息分析对上海燃气负荷数据中预先选择的7个特征进行降维和分析, 提取影响上海燃气负荷的关键因子. 根据前文的步骤采用Python 3.7得到了各主成分的互信息的贡献率, 如图5所示. 前3个主成分的互信息累计贡献率达到了77.35%, 大于选取主成分个数的累计互信息贡献率的阈值, 故确定主成分个数为3个, 使数据的维度减少了4维.

|
图 5 主成分的互信息和累计互信息贡献率 |
因为燃气负荷数据之间的相关性极强, 采用互信息极大旋转, 计算出各主成分在各个特征上的成分负载, 如表1所示. 对于燃气负荷而言, 天气因素和时间都会对燃气负荷产生影响. 温差对第 2 主成分的相关系数绝对值超过了0. 85, 相对其他因子贡献较大; 月份对第1主因子贡献最大; 加热系数对第 3 主因子贡献最大. 在温度因素上, 城市短期负荷主要受到温差和加热系数的影响, 当温差或加热系数变大的时候, 燃气负荷会呈现出明显的上升趋势. 在时间因素上, 月份在冬季的时候需要更多的燃气来满足人们的日常需求.
| 表 1 互信息PCA的主成分荷载矩阵 |
对比一下MIPCA和PCA的降维数据如图6所示. 两种降维方法后每个主成分与燃气负荷的互信息, 两种降维方式都去除掉特征与特征之间的相关性, 但是在互信息PCA中保留住互信息为0.373的主成分, 而在传统的PCA中不存在此主成分. 所以相比于传统PCA而言, 使用互信息作为选取主成分的标准不仅可以在降维地过程中考虑特征与预测值的关系, 还可以更好地提取与燃气负荷值更为相关的特征.

|
图 6 两种降维后数据与燃气负荷的互信息 |
2.2 EEMD分解结果
针对燃气时间序列数据非平稳、非线性的特点, 使用EEMD对数据信号进行平稳化处理, 将包含大量高频分量、噪声的燃气数据分解为IMF分量, 减少模型拟合的难度.
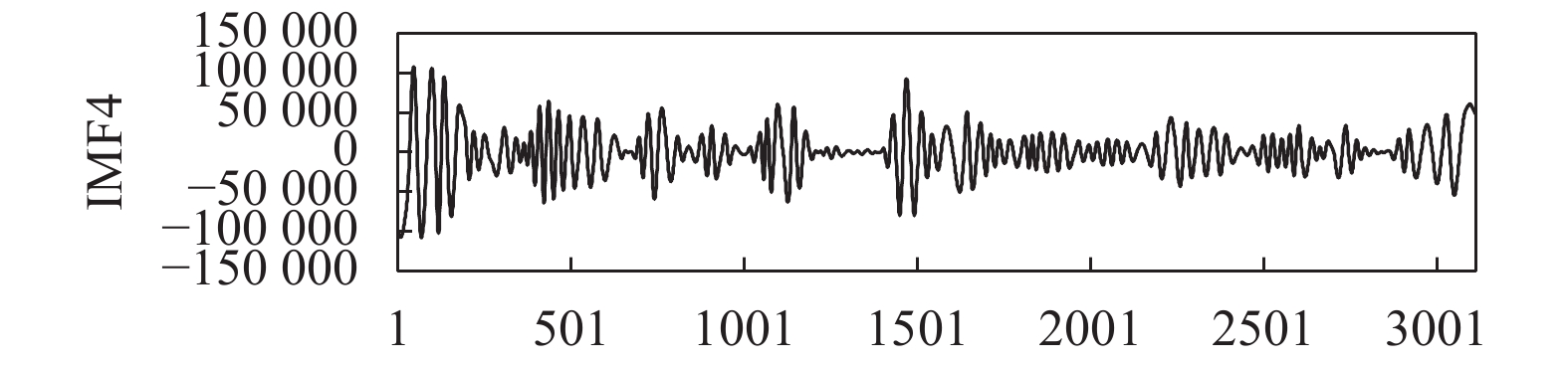
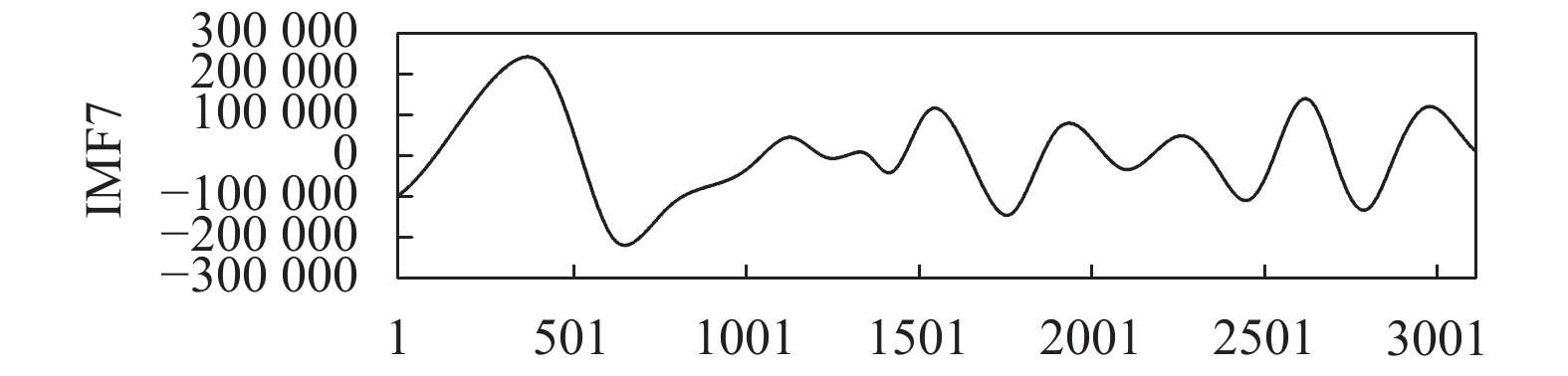
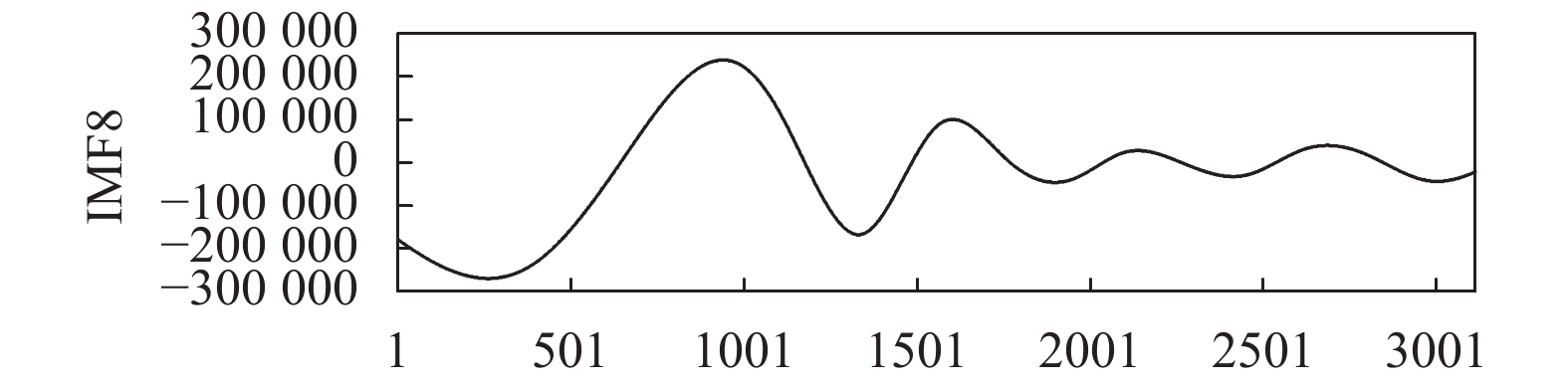
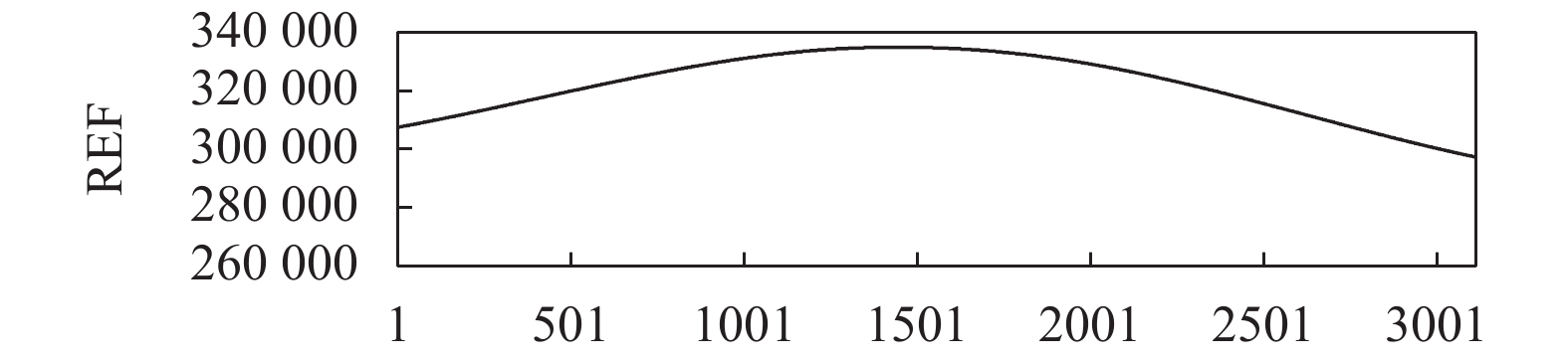
将上海2005年的燃气数据座位实例进行EEMD分解, 得到10组频率由高到低的本征模态函数及余波, 如图7~图16所示. 在EEMD分解后, 各个IMF分量频率比较稳定, 并没有出现明显的模态混叠现象. IMF1到IMF4为燃气数据的高频分量, 主要收到随机人为因素影响, 预测较为困难. IMF5到IMF8为中频分量, 具有一定的周期性. 剩余为中低频分量, 表示了燃气的总体趋势和变化规律. EEMD模型通过将原始燃气序列分解为含有负荷不同波动局部特征的若干IMF分量, 作为模型的输入再进行预测.

|
图 7 EEMD 分解结果-IMF1 |

|
图 8 EEMD 分解结果-IMF2 |

|
图 9 EEMD 分解结果-IMF3 |
|
图 10 EEMD 分解结果-IMF4 |

|
图 11 EEMD 分解结果-IMF5 |

|
图 12 EEMD 分解结果-IMF6 |
|
图 13 EEMD 分解结果-IMF7 |
|
图 14 EEMD 分解结果-IMF8 |

|
图 15 EEMD 分解结果-IMF9 |
|
图 16 EEMD 分解结果-REF |
2.3 模型参数与预测结果
建立LSTM模型采用rmsprop优化器和MAE损失函数进行训练. LSTM有两层, 每层的节点数分别为5和3, 使用前7天的标准化后的数据预测下一天的燃气负荷值, 模型训练的迭代过程入图17所示.

|
图 17 模型训练迭代过程 |
为了验证 EEMD-MIPCA-LSTM 算法的可靠性, 本文还采用LSTM算法、PCA-LSTM算法、PCCA-LSTM[9]算法和MIPCA-LSTM算法来预测上海吴淞地区日燃气负荷量. 根据图18所示, 本文所提方法在燃气急剧变化的时期, 预测精度较高, 在时间序列 1 到 150之间的预测数据较平稳的燃气真实值动荡较大, 导致预测曲线与真实数据有一定的偏差, 和LSTM、PCA-LSTM、PCCA-LSTM以及MIPCA-LSTM相比较, EEMD-MIPCA-LSTM预测精度有明显的提升, 如图19所示.

|
图 18 EEMD-MIPCA-LSTM预测结果 |

|
图 19 模型对照结果 |
使用平均绝对误差、均方根误差和平均绝对百分比误差作为衡量指标, 如式(14)~式(16), 计算结果如表2所示.
| 表 2 仿真误差 |
平均绝对误差(MAE):
| $MAE = \frac{1}{n}\sum\limits_{i = 1}^n {\left|{y_i} -{\hat{ y_i}} \right|} $ | (14) |
均方根误差(RMSE):
| $RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({y_i} - {\hat{y_i}} )}^2}} } $ | (15) |
平均绝对百分比误差(MAPE):
| $MAPE = 100\frac{1}{n}\sum\limits_{i = 1}^n {\left|\frac{{{y_i} - {\hat{y_i}}}}{{{y_i}}}\right|} $ | (16) |
其中,
根据表2的数据, 可以得到以下结论:
(1)准确的燃气负荷预测是困难的, 主要原因是它受到多种因素影响, 主要包括: 天气因素和时间因素. 这两大因素难以量化. 在通过LSTM和PCA-LSTM的对比中, PCA-LSTM减少数据的纬度并减少特征之间相关性, 提升了燃气负荷预测的精度.
(2) 在PCCA和PCA的比较中, 不仅去除特征之间的相关性, 还提取出与燃气负荷皮尔逊相关系数高的主成分, 提高了燃气的预测精度[9].
(3) 燃气预测具有非线性的特征, 使用皮尔逊相关系数并不能发掘出特征与燃气负荷之间的关系, 通过加入互信息分析, 更好地挖掘出燃气负荷与特征的关系, 在MIPCA-LSTM和PCCA-LSTM对比中, MIPCA-LSTM的预测精度更高.
(4) 燃气负荷数据易受多种因素的影响而呈现时空分布不均匀, 难以进行较精准的短期负荷预测. EEMD预测模型通过将原始燃气序列分解为含有负荷不同波动局部特征的若干IMF分量, 作为模型的输入再进行预测. 结果表明此模型不仅能提高燃气负荷的精准度, 减少预测模型复杂度, 而再以组合的形式分开输入时可以最大改善预测效果, 预测误差为6.36%, 优于其他模型.
3 实验分析本文围绕上海燃气负荷预测提出了一种针对高频分量多, 周期性弱的能源预测方法, 使用EEMD分解将高频燃气数据分解为频率从高到低的若干IMF分量.
在外部因素的处理中, 结合燃气数据非线性的特点, 在PCA中加入互信息分析, 在去除特征之间相关性的同时, 找到与负荷数据更具有任意函数关系的特征. 最后, 使用LSTM对分解后的各IMF分量进行预测, 将所有结果依次叠加, 实现高可靠性的准确预测. 实验结果表明, 本文提出的方法相对于单一的预测模型以及PCA-LSTM等组合模型更能预测出燃气负荷的变化趋势, 对负荷的局部细节也具有较高的预测精度.
| [1] |
Tamba JG, Essiane SN, Sapnken EF, et al. Forecasting natural gas: A literature survey. International Journal of Energy Economics and Policy, 2018, 8(3): 216-249. |
| [2] |
Laib O, Khadir MT, Mihaylova L. Toward efficient energy systems based on natural gas consumption prediction with LSTM recurrent neural networks. Energy, 2019, 177: 530-542. |
| [3] |
Wu ZH, Huang NE. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. |
| [4] |
刘晓琼, 孙曦亮, 刘彦随, 等. 基于REOF-EEMD的西南地区气候变化区域分异特征. 地理研究, 2020, 39(5): 1215-1232. DOI:10.11821/dlyj020190387 |
| [5] |
邓带雨, 李坚, 张真源, 等. 基于EEMD-GRU-MLR的短期电力负荷预测. 电网技术, 2020, 44(2): 593-602. |
| [6] |
王晓霞, 徐晓钟, 张彤, 等. 基于集成深度学习算法的燃气负荷预测方法. 计算机系统应用, 2019, 28(12): 47-54. DOI:10.15888/j.cnki.csa.007168 |
| [7] |
Feldman D, Schmidt M, Sohler C. Turning Big data into tiny data: Constant-size coresets for k-means, PCA and projective clustering. Proceedings of the 24th Annual ACM-SIAM Symposium on Discrete Algorithms. New Orleans, LA, USA. 2018. 1434–1453.
|
| [8] |
Bianchi FM, De Santis E, Rizzi A, et al. Short-term electric load forecasting using echo state networks and PCA decomposition. IEEE Access, 2015, 3: 1931-1943. |
| [9] |
Wei N, Li CJ, Duan JH, et al. Daily natural gas load forecasting based on a hybrid deep learning model. Energies, 2019, 12(2): 218. |
| [10] |
徐玚, 徐晓钟. 基于ESN和改进RBFNN的城市燃气负荷预测. 计算机系统应用, 2019, 28(3): 28-35. DOI:10.15888/j.cnki.csa.006798 |
| [11] |
董浩, 程鹏, 李玲玲. 深度学习算法在电力系统短期负荷预测中的应用. 电气时代, 2017(2): 82-84. |
| [12] |
陈亮, 王震, 王刚. 深度学习框架下LSTM网络在短期电力负荷预测中的应用. 电力信息与通信技术, 2017, 15(5): 8-11. |
| [13] |
Fan GF, Peng LL, Zhao XJ, et al. Applications of hybrid EMD with PSO and GA for an SVR-based load forecasting model. Energies, 2017, 10(11): 1713. DOI:10.3390/en10111713 |
 2020, Vol. 29
2020, Vol. 29



