2. 中国铁路西安局集团有限公司 宝鸡供电段, 宝鸡 721015
2. Baoji Power Supply Section, China Railway Xi’an Bureau Group Co. Ltd., Baoji 721015, China
弓网系统之间接触压力的波动直接影响着高速列车受流能力, 接触压力过大将增大弓网的磨耗, 过小将造成弓网之间的离网使机车断电, 压力的波动将增大弓网的离网率. 为了提高高速列车的受流能力降低离网率, 传统的解决方法是提高接触网的刚度增加接触线的张力, 但是此类方法成本过高不易实施, 近几年国内外很多学者开始研究受电弓的主动控制, 利用先进的控制算法使受电弓在适当的压力范围内进行自适应控制, 以提高系统的动态性能, 改善高速列车的动态受流能力[1]. 在受电弓的主动控制中弓网耦合系统要求有较高的鲁棒性和动态性能, 因此采用线性二次型最优控制(Linear Quadratic Regulator, LQR). 在控制器的设计中只需要设定适合系统动态响应的状态变量和接触压力的加权矩阵, 最终得出系统的状态反馈控制率, 进一步提高系统的动态响应[2]. 但在LQR设计过程中, 权矩阵Q和R的计算往往是设计者根据以往经验采用尝试法来确定[2-4].
近几年在LQR的设计过程中提到了很多改进策略, 文献[5]通过提高系统的可控范围和动态性能, 结果过于局限, 应用于其他系统效果不理想, 文献[6]通过对Q和R进行粒子群理论的优化, 导致结果出现局部过小得不到全局最优的目的. 本文选择一种高效的全局搜索算法即遗传算法(Genetic Algorithm, GA), 通过弓网系统的动态性能设计合适的目标函数, 得出全局优化的权矩阵Q和R, 进一步算出适合系统的最优状态反馈控制率K, 通过Matlab/Simulink仿真对数据分析得出该方法的正确性与有效性.
1 弓网耦合动力学模型弓网耦合动力模型[7]是研究受电弓主动控制的必要条件, 由于弓网动力学模型的构建与计算很复杂, 因此在研究受电弓主动控制时, 接触网模型的建立采用有限元法, 受电弓模型的建立采用归算质量法[8].
1.1 接触网模型采用我国经常使用的接触网类型简单链型悬挂方式, 接触网模型的建立关键在于其刚度的计算, 由于随着机车速度的变化两根接触网柱之间以及接触网柱附近的接触网刚度都在不断地变化, 因此为了简化便于模型的建立, 文献[9]将接触网作为变刚度弹性系统, 通过有限元方法计算出实际刚度曲线, 利用最小二乘法对刚度曲线进行拟合运算, 最终得到简化后的接触网刚度公式:
| $ \begin{split} k(t) \!=\! &\mathop k\nolimits_0 \left[ {[1 \!+\! \mathop \varepsilon \nolimits_1 \cos \left(\frac{{2\pi v}}{H}t\right) \!+\! \mathop \varepsilon \nolimits_2 \cos \left(\frac{{2\pi v}}{{\mathop H\nolimits_1 }}t \right) \!+\! \mathop \varepsilon \nolimits_3 \mathop {\cos }\nolimits^2 \left(\frac{{2\pi v}}{H}t \right) } \right.\\ &\!+\!\left. {\mathop \varepsilon \nolimits_4 \mathop {\cos }\nolimits^2 \left(\frac{{2\pi v}}{H}t \right) + \mathop \varepsilon \nolimits_5 \mathop {\cos }\nolimits^2 \left(\frac{{2\pi v}}{{\mathop H\nolimits_1 }}t \right)} \right] \end{split} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!$ | (1) |
其中, k0为接触网的平均刚度, 单位为N·m–1, v为机车的运行速度, 单位为m/s, H为两根接触网柱之间的距离, 即为跨距, 单位为m, H1为接触网中相邻两个吊弦之间的距离, 单位为m,
| 表 1 接触网参数 |
通过Matlab/Simulink软件仿真分析, 机车在不同运行速度下接触网的刚度变化曲线如图1所示. 仿真分析得知, 在机车速度一定的条件下, 接触网的刚度数值在一个跨距的变化趋势为由大到小再到大的过程, 这是因为一个跨距两端由于支柱和限位器的作用使接触网线处于绷紧状态, 此时接触网刚度值呈现较大的数值, 随着跨距的距离增大接触网线由于其重力和侧拉力的作用出现松动现象, 此时接触网刚度值呈现降低趋势, 在跨距中间点处接触网刚度值达到最小, 仿真结果符合实际情况.

|
图 1 接触网刚度变化 |
随着机车速度的提高, 机车通过一个跨距的时间缩短, 接触网刚度值变化的周期也逐渐缩短, 表2列出了机车在不同速度下接触网刚度值的评价性能指标, 其数值也各不相同, 说明接触网的刚度值与机车速度成非线性关系.
| 表 2 不同速度刚度值评价性能指标 |
1.2 弓网系统模型
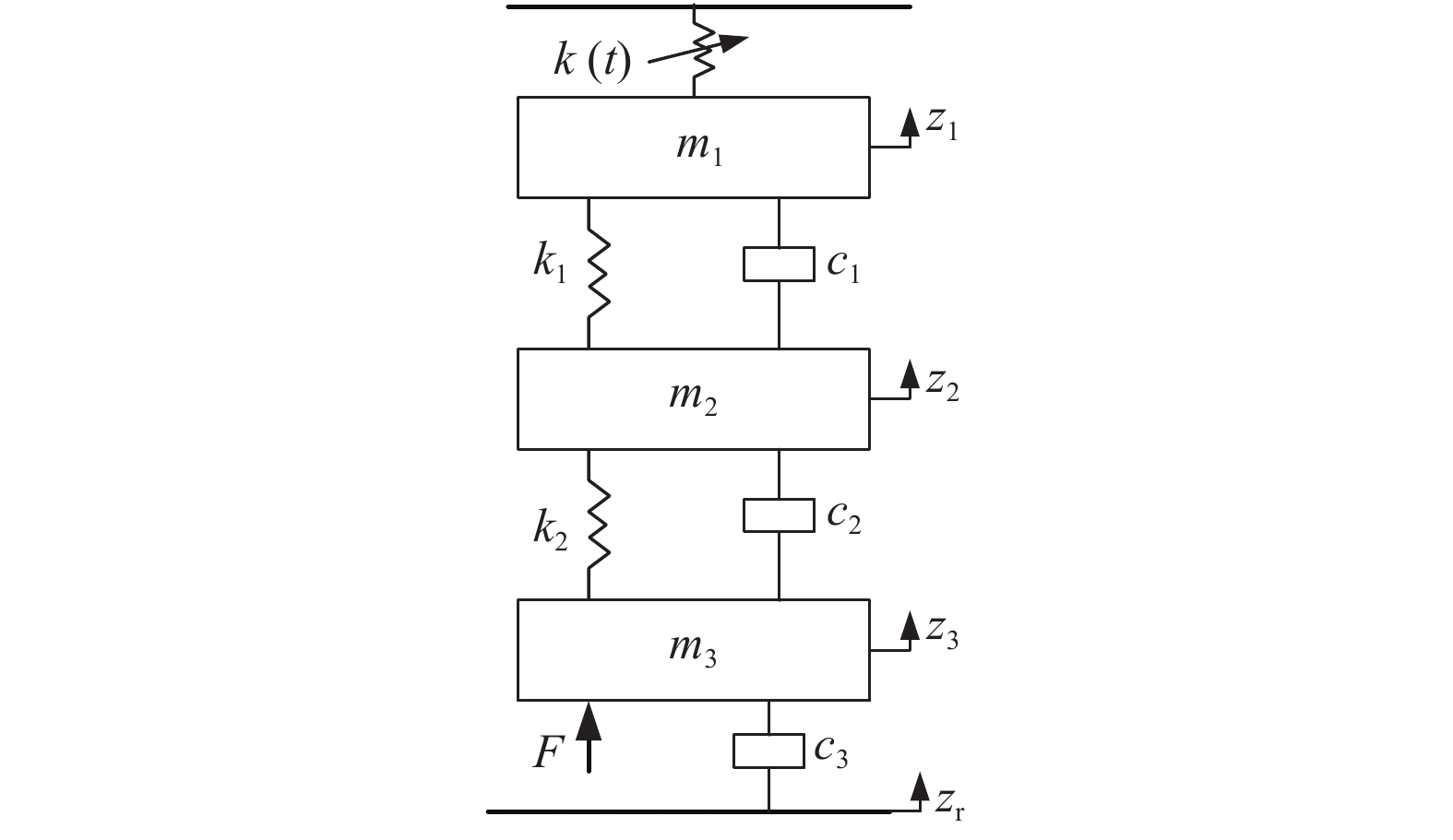
对受电弓建立模型时, 由于其是一个系数可变的非线性系统[9,10], 为了简化模型的建立, 通常采用归算质量法, 也就是将受电弓作为线性处理, 根据受电弓中重要的质量模块分为一元质量模型、二元质量模型、三元质量模型, 一般质量模块越多对受电弓模型的建立越精确, 往往在线性模型建立的过程中取受电弓三个部位的质量参数, 即三元质量模型, 如图2所示.
|
图 2 受电弓三元质量模型 |
根据受电弓的三元质量模型及其受力分析得到弓网系统的微分方程:
| $\left\{ {\begin{array}{l} \!\! \!\!{\mathop m\nolimits_1 \mathop {\mathop {\textit{z}}\nolimits_1 }\limits^{ \cdot \cdot } + \mathop k\nolimits_1 (\mathop {\textit{z}}\nolimits_1 - \mathop {\textit{z}}\nolimits_2 ) + \mathop c\nolimits_1 {( \mathop {\mathop{\textit{z}}\nolimits_1 }\limits^ \cdot }- \mathop {\mathop {\textit{z}}\nolimits_2 }\limits^ \cdot ) + k(t)\mathop {\textit{z}}\nolimits_1 = 0} \\ \!\!\!\!{\mathop m\nolimits_2 \mathop {\mathop {\textit{z}}\nolimits_2 }\limits^{ \cdot \cdot } \!+\! \mathop k\nolimits_1 (\mathop {\textit{z}}\nolimits_2 \!-\! \mathop {\textit{z}}\nolimits_1 ) \!+\! \mathop k\nolimits_2 (\mathop {\textit{z}}\nolimits_2 \!-\! \mathop {\textit{z}}\nolimits_3 ) \!+\! \mathop c\nolimits_1 {(\mathop {\mathop{\textit{z}}\nolimits_2 }\limits^ \cdot} \!-\! \mathop {\mathop {\textit{z}}\nolimits_1 }\limits^ \cdot ) + \mathop c\nolimits_2 {(\mathop {\mathop{\textit{z}}\nolimits_2 }\limits^ \cdot }- \mathop {\mathop {\textit{z}}\nolimits_3 }\limits^ \cdot ) = 0} \\ \!\!\!\!{\mathop m\nolimits_3 \mathop {\mathop {\textit{z}}\nolimits_3 }\limits^{ \cdot \cdot } + \mathop k\nolimits_2 (\mathop {\textit{z}}\nolimits_3 - \mathop {\textit{z}}\nolimits_2 ) + \mathop c\nolimits_2 {(\mathop {\mathop{\textit{z}}\nolimits_3 }\limits^ \cdot} - \mathop {\mathop {\textit{z}}\nolimits_2 }\limits^ \cdot ) + \mathop c\nolimits_3 {(\mathop {\mathop{\textit{z}}\nolimits_3 }\limits^ \cdot} - \mathop {\mathop {\textit{z}}\nolimits_r }\limits^ \cdot ) = F} \end{array}} \right.$ | (2) |
根据质量模型理论, m1, m2, m3分别为受电弓等效三元质量模型中的弓头质量, 上框架质量, 下框架质量; ki(i=1,2), ci(i=1,2,3)分别表示弓头与上框架以及下框架的等效刚度及其阻尼值; 受电弓的静抬升力为F, zr机车对受电弓的干扰与振动, 在此可以模拟为噪声信号. 接触网的等效刚度值为k(t). 弓网系统的微分方程是一个时变参激振动系统, 为了便于分析与仿真, 将其写成状态方程的形式, 其状态变量为:
| $\begin{split} X & =\mathop {[\begin{array}{*{20}{c}} {\mathop x\nolimits_1 }&{\mathop x\nolimits_2 }&{\mathop x\nolimits_3 }&{\mathop x\nolimits_4 }&{\mathop x\nolimits_5 }&{\mathop x\nolimits_6 } \end{array}]}\nolimits^{\rm T}\\ &= [\begin{array}{*{20}{c}} {\mathop {\textit{z}}\nolimits_1 }&{\mathop {\mathop {\textit{z}}\nolimits_1 }\limits^ \cdot }&{\mathop {\textit{z}}\nolimits_2 }&{\mathop {\mathop {\textit{z}}\nolimits_2 }\limits^ \cdot }&{\mathop {\textit{z}}\nolimits_3 }&{\mathop {\mathop {\textit{z}}\nolimits_3 }\limits^ \cdot } \end{array}] \end{split}$ | (3) |
则, 状态方程有:
| $\left\{ {\begin{array}{l} {\mathop x\limits^ \cdot (t) = Ax(t) + Bu(t) + Dw(t)} \\ {y(t) = cx(t)} \end{array}} \right.$ | (4) |
其中,
| $ A = \left[ {\begin{array}{*{20}{c}} 0\!\!\!\!&\!\!\!\!1\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!0 \\ { - \dfrac{{\mathop k\nolimits_1 + k(t)}}{{\mathop m\nolimits_1 }}}\!\!\!\!&\!\!\!\!{ - \dfrac{{\mathop c\nolimits_1 }}{{\mathop m\nolimits_1 }}}\!\!\!\!&\!\!\!\!{\dfrac{{\mathop k\nolimits_1 }}{{\mathop m\nolimits_1 }}}\!\!\!\!&\!\!\!\!{\dfrac{{\mathop c\nolimits_1 }}{{\mathop m\nolimits_1 }}}\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!0 \\ 0\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!1\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!0 \\ {\dfrac{{\mathop k\nolimits_1 }}{{\mathop m\nolimits_2 }}}\!\!\!\!&\!\!\!\!{\dfrac{{\mathop c\nolimits_1 }}{{\mathop m\nolimits_2 }}}\!\!\!\!&\!\!\!\!{ - \dfrac{{\mathop k\nolimits_1 + \mathop k\nolimits_2 }}{{\mathop m\nolimits_2 }}}\!\!\!\!&\!\!\!\!{ - \dfrac{{\mathop c\nolimits_1 + \mathop c\nolimits_2 }}{{\mathop m\nolimits_2 }}}\!\!\!\!&\!\!\!\!{\dfrac{{\mathop k\nolimits_2 }}{{\mathop m\nolimits_2 }}}\!\!\!\!&\!\!\!\!{\dfrac{{\mathop c\nolimits_2 }}{{\mathop m\nolimits_2 }}} \\ 0\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!1 \\ 0\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!{\dfrac{{\mathop k\nolimits_2 }}{{\mathop m\nolimits_3 }}}\!\!\!\!&\!\!\!\!{\dfrac{{\mathop c\nolimits_2 }}{{\mathop m\nolimits_3 }}}\!\!\!\!&\!\!\!\!{ - \dfrac{{\mathop k\nolimits_2 }}{{\mathop m\nolimits_3 }}}\!\!\!\!&\!\!\!\!{ - \dfrac{{\mathop c\nolimits_3 + \mathop c\nolimits_2 }}{{\mathop m\nolimits_3 }}} \end{array}} \right], $ |
| $ B = \mathop {\left[\begin{array}{*{20}{c}} 0&0&0&0&0&{\dfrac{1}{{\mathop m\nolimits_3 }}} \end{array}\right]}\nolimits^{\rm T}, $ |
| $ \begin{split} & C = \left[ {\begin{array}{*{20}{c}} {k(t)}&{0}&{0}&{0}&{0}&{0} \end{array}} \right],\\ & D = {\left[ {\begin{array}{*{20}{c}} 0&{0}&{0}&{0}&{0}&{\dfrac{{{\rm{ }}{c_3}}}{{{\rm{ }}{m_3}}}} \end{array}} \right]^{\rm T}}. \end{split} $ |
根据弓网系统耦合动力学模型的状态方程, 以DSA350型受电弓为研究对象, 其参数如表3所示, 设定列车在不同速度下, 以100 N的静态升力为参考数值, 通过Matlab/Simulink软件仿真弓网系统中影响受电弓主动控制的两个重要动态性能参数, 即弓头位移和接触压力的变化.
| 表 3 DSA350型受电弓参数 |
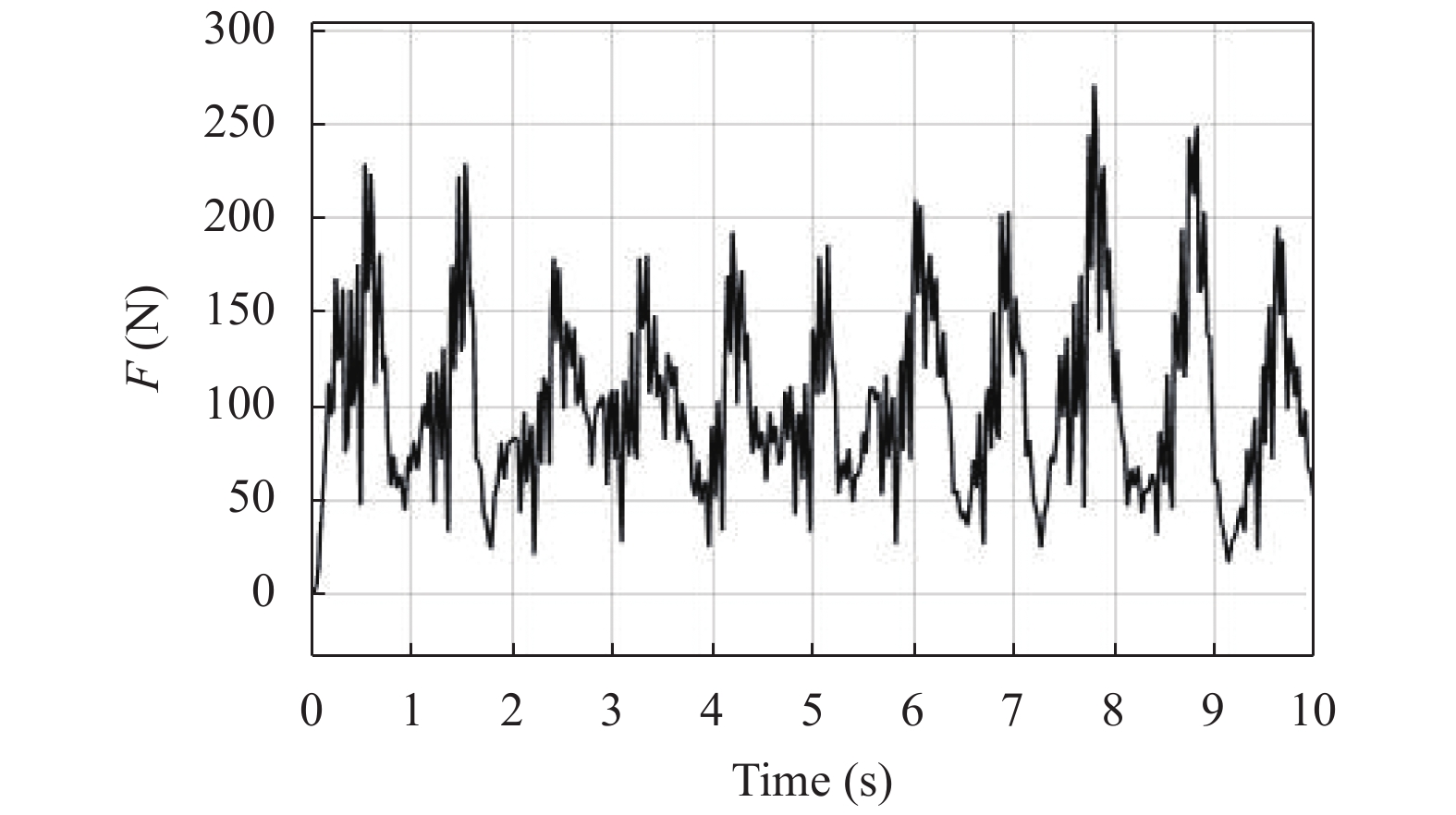
图3、图4分别为列车在速度200 km/h下受电弓弓头的位移和接触压力的变化曲线仿真结果. 通过仿真结果得出接触压力在100 N的静抬升力附近波动, 其波动范围为(0, 271), 弓头随着接触压力的波动而持续波动, 其波动范围(0, 0.108), 对速度120 km/h、200 km/h、250 km/h仿真结果, 列出其接触网压力以及弓头位移评价性能参数, 如表4、表5所示, 以及相对应的柱状对比图如图5, 图6所示. 由表4可知随着速度的增大接触压力逐渐增大. 由表5可知弓头的移动位移逐渐增大, 当达到250 km/h时弓头的波动位移减小.
2 最优控制器的设计由图3、图4仿真结果可知, 机车在运行时随着速度的不断提高弓网之间接触压力与弓头位移的波动逐渐加大, 导致弓网离线率升高, 最终影响机车的正常运行, 为了减小波动的幅值与频率降低离网率, 提高高速列车的受流能力, 在受电弓主动控制中引入最优控制器利用系统的耦合动力学模型, 采用线性二次型最优控制理论(LQR)设计受电弓主动控制器.
|
图 3 接触网压力的变化 |

|
图 4 弓头位移的变化 |
| 表 4 接触网压力评价性能参数 |
| 表 5 弓头位移评价性能参数 |

|
图 5 接触压力参数柱状图比较 |

|
图 6 弓头位移参数柱状图比较 |
最优控制器设计[11]的目的就是系统利用恒定的静抬升力来控制系统最终的状态值, 使系统最终的接触压力与弓头位移的误差和能量最小化. 因此LQR的设计应首先确定性能指标, 系统的状态方程如下:
| $\left\{\begin{split} & \mathop x\limits^ \cdot = Ax + Bu \\ & \mathop y\limits^ \cdot = Cx + Du \\ \end{split} \right.$ |
一般情况下, 控制的目标是使系统性能指标达到最小化, 那么设定一个状态反馈规律:
| $u(t) = - Kx(t)$ |
即弓网耦合系统输入最优控制力为:
| $\mathop F\nolimits_u = - KX = \mathop { - R}\nolimits^{ - 1} \mathop B\nolimits^{\rm T} PX(t)$ |
式中, P为Riccati方程的解, 即:
| $ - PA - \mathop A\nolimits^{\rm T} P + P\mathop {BR}\nolimits^{ - 1} \mathop B\nolimits^{\rm T} P - Q = 0$ |
式中, Q, R分别为权矩阵; K为反馈矩阵.
根据线性二次型最优控制理论[12], 结合弓网耦合动力学模型, 随着列车速度的提高, 相应的受电弓各质量部件运动速度也不断提高. 为了限制弓头质量模块和框架质量模块的运动速度, 应当在加权矩阵相应的位置选取较大的数值来抑制其运行的速度, 而随着列车运行过程中由于线路等工况使弓头和框架随着接触网高度的变化而变化, 因此其位移的变化要具有一定的灵活性, 在加权矩阵相应的位置不需要设置加权数值, 即不需要对其进行抑制.
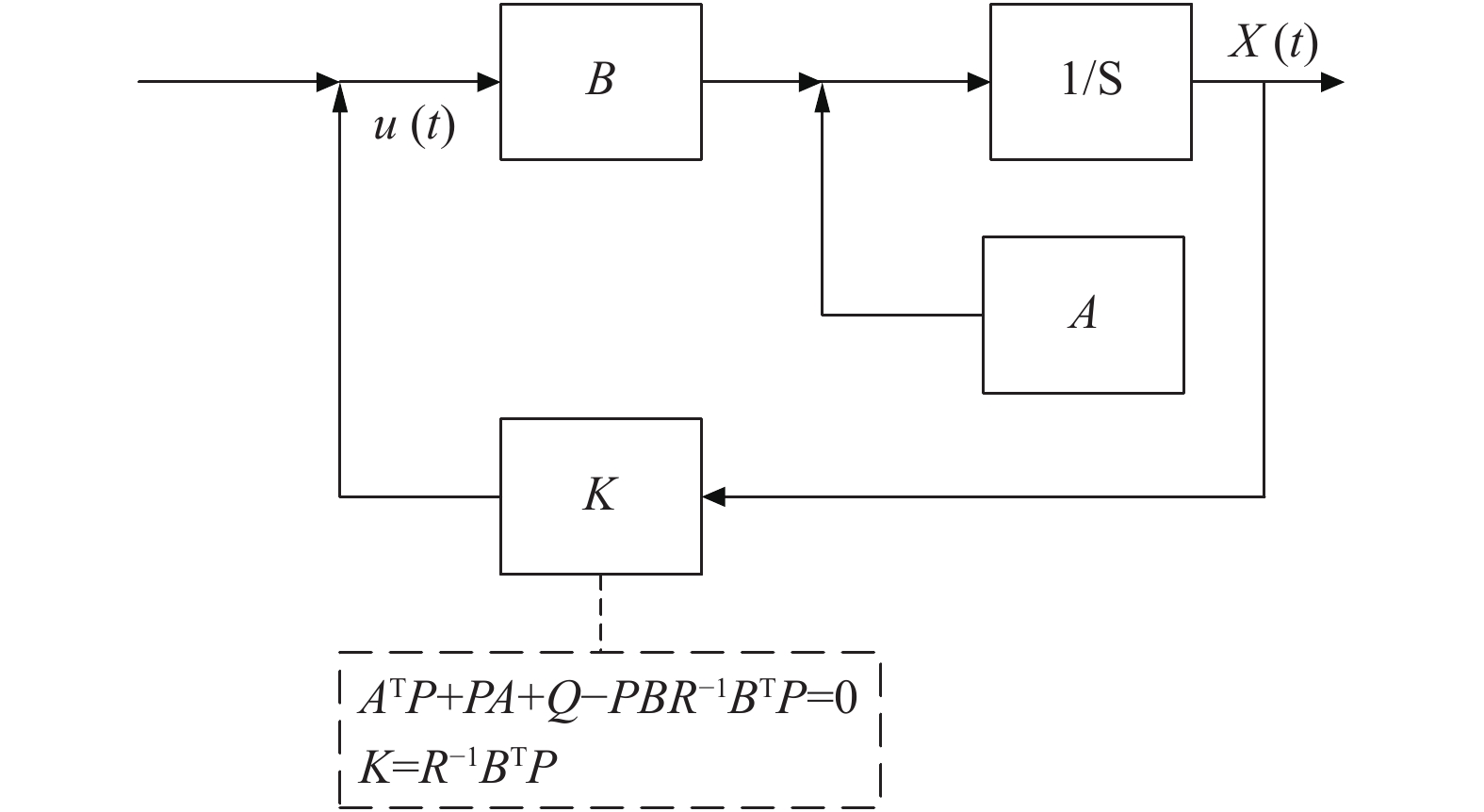
以DSA350型受电弓参数为基础, 根据LQR结构框图如图7所示, 得出计算反馈矩阵K的步骤:
(1) 选择参数矩阵Q, R;
(2) 求解Riccati方程得到矩阵P;
(3) 计算
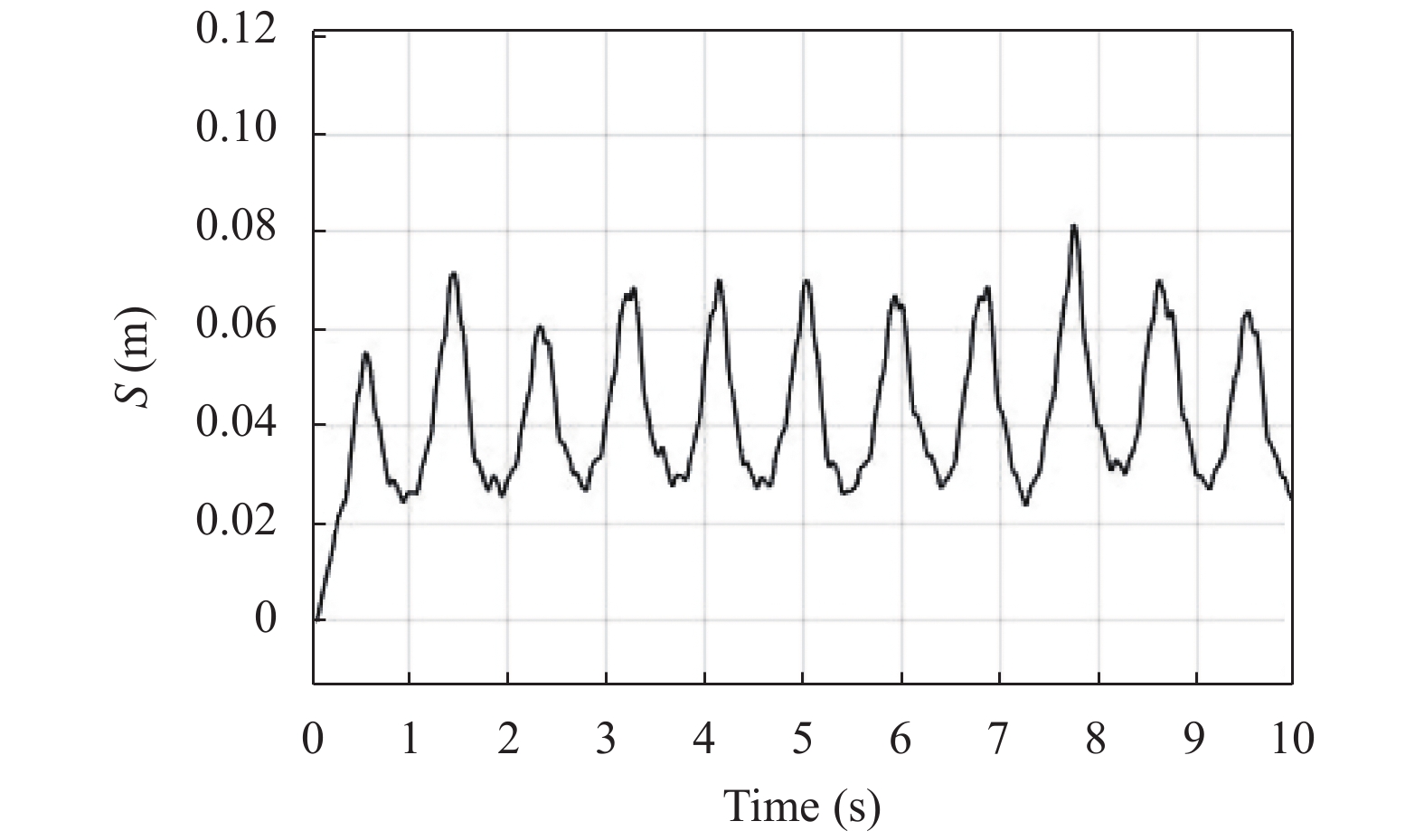
依据以上求解过程及其LQR结构图, 通过Matlab/Simulink软件仿真得到受电弓在最优主动控制器作用下弓网系统接触压力与弓头位移波动变化曲线, 如图8, 图9所示, 通过仿真波形的分析得出接触压力和弓头位移的波动程度得到降低.
|
图 7 LQR结构图 |

|
图 8 基于LQR接触网压力波动曲线 |
|
图 9 基于LQR弓头位移波动曲线 |
由表6可知, 基于LQR控制器的弓网系统与无主动控制器的弓网系统相比接触压力最大值标准差值分别减小27.1%与19.75%, 平均值增大9.9%, 表明接触压力的波动范围减小, 弓头位移最大值、平均值以及标准差分别减小25%, 3.3%, 40.5%, 表明弓头位移的波动范围也减小, 说明LQR控制器有效地抑制了接触网压力与弓头位移的波动, 稳定性得到提高, 由于在弓网模型中加入了噪声的扰动, 说明控制系统对噪声有一定的鲁棒性.
| 表 6 与无主动控制LQR各参数对比 |
3 基于GA对加权矩阵的优化
根据LQR控制器对受电弓的主动控制仿真图分析可知, 接触网压力与弓头位移的波动幅度减小程度效果不明显, 主要是由于LQR的求解过程中加权矩阵Q和R的计算是建立在经验尝试的基础之上[13,14], 使得结果呈现局部最优解, 因此为了达到更好抑制系统接触力与弓头位移波动, 利用GA理论的全局最优搜索能力, 来确定加权矩阵, 最终提高控制器的效率与性能. 由弓网耦合动力学模型可知, 该系统有6个状态变量, 属于多变量系统, 根据受电弓弓网系统的动态性能参数, 选取R=10–6,
| $ Q = \left[ {\begin{array}{*{20}{c}} {\mathop Q\nolimits_{11} }&{}&{}&{}&{}&{}\\ {}&{\mathop Q\nolimits_{22} }&{}&{}&{}&{}\\ {}&{}&{\mathop Q\nolimits_{33} }&{}&{}&{}\\ {}&{}&{}&{\mathop Q\nolimits_{44} }&{}&{}\\ {}&{}&{}&{}&{\mathop Q\nolimits_{55} }&{}\\ {}&{}&{}&{}&{}&{\mathop Q\nolimits_{66} } \end{array}} \right],\;{{R}} = {10^{ - 6}} $ |
在进行GA-LQR算法求解加权矩阵时, 需要引入约束处理条件[15], 即加权系数适应度函数值, 由于受电弓主动控制过程中, 接触力和弓头位移是影响弓网系统的两个主要因素, 因此在设定适应度函数值时, 只需要对接触力和弓头位移进行条件约束, 加权系数适应度函数值:
| $\left\{\begin{split} &\min L = \frac{{JY(X)}}{{\mathop {JY}\nolimits_{{\rm{pas}}} }} + \frac{{GT(X)}}{{\mathop {GT}\nolimits_{{\rm{pas}}} }},\;{X \in (0,1)} \\ &{\rm s.t.}\left\{ {\begin{array}{*{20}{c}} {JY < \mathop {JY}\nolimits_{\rm pas} } \\ {GT < \mathop {GT}\nolimits_{\rm pas} } \end{array}} \right. \end{split}\right.$ |
其中, JY, GT分别代表了弓网之间的接触力和弓头位移的均方根, JYpas, GTpas为弓网系统相应的性能.
基于GA对加权矩阵Q的优化步骤如图10所示.

|
图 10 GA-LQR程序结构 |
依据以上求解过程及其GA-LQR算法步骤结构图, 通过Matlab/Simulink软件仿真得出Q值:
通过LQR的运算程序, 计算得到K值:
| $ \begin{split} {{K}} =& 1.0{\rm{e}} + 03\\ &*\left[ { - 0.8782\;0.0848\; - 3.9298\;0.1130\;3.7418\;0.5062} \right] \end{split} $ |
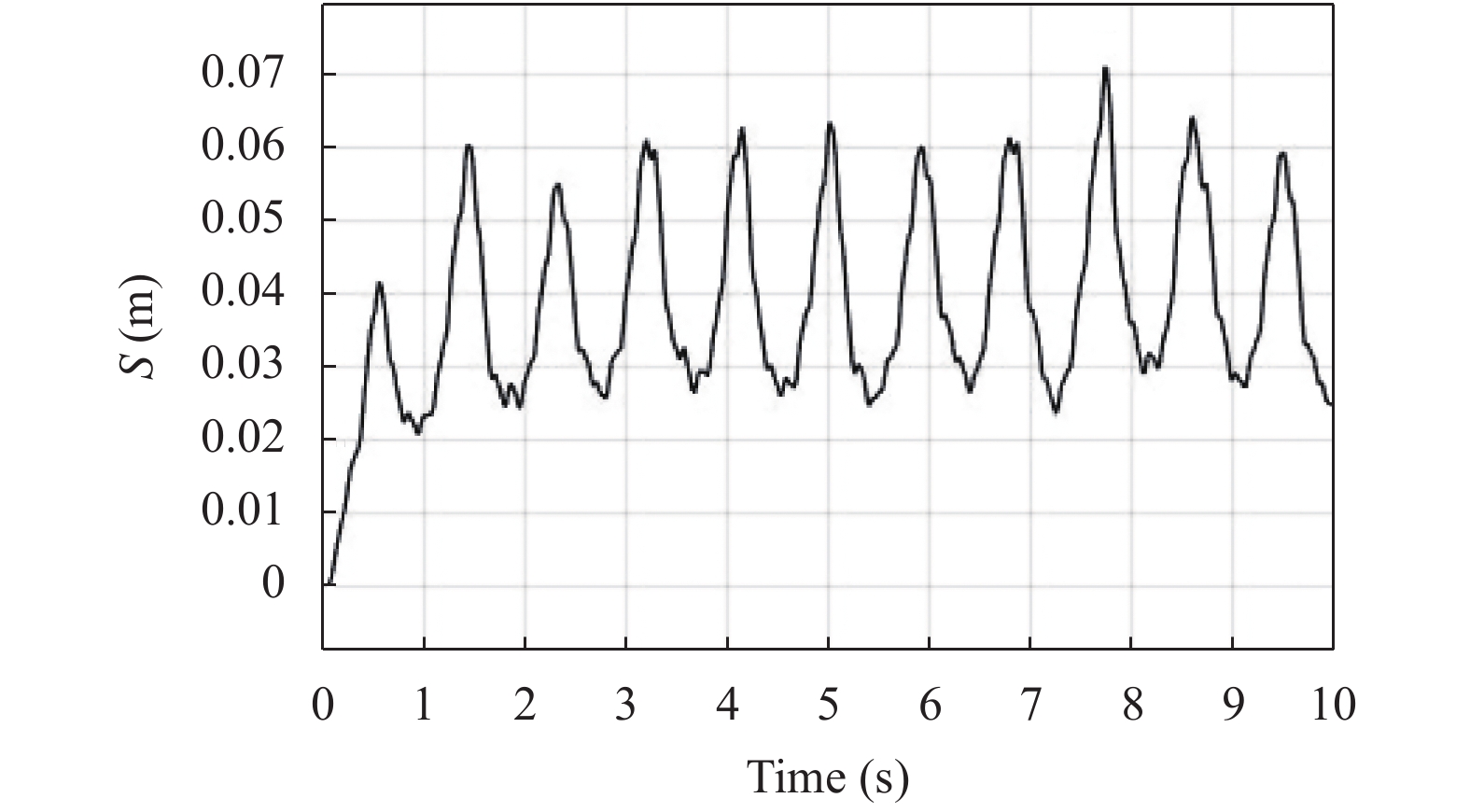
从而得到受电弓在最优主动控制器作用下弓网系统接触压力与弓头位移波动变化曲线, 如图11, 图12所示, 通过仿真波形的分析得出接触压力和弓头位移的波动范围小于优化之前的控制器, 说明GA-LQR控制算法的稳定性在弓网系统中优于LQR.

|
图 11 基于GA-LQR接触网压力波动曲线 |
通过表7得出对于基于GA-LQR控制器的弓网系统与LQR主动控制器的弓网系统相比接触压力最大值、平均值、标准差值分别减小14.3%、8.83%、11.53%, 弓头位移最大值、平均值以及标准差分别减小13.58%, 7.31%, 10%, 表明基于GA-LQR主动控制器的弓网系统接触压力与弓头位移的波动范围较LQR主动控制器均减小, 说明GA-LQR控制器克服了LQR的缺点, 更加有效地提高了弓网系统的稳定性与鲁棒性.
|
图 12 基于GA-LQR弓头位移波动曲线 |
| 表 7 与LQR相比GA-LQR各参数对比 |
3种模式下接触网压力与弓头位移的波动参数对比如表8所示, 随着主动控制算法的引入与改进, 弓网系统之间的接触网压力与弓头位移的标准差减小, 波动程度受到了抑制, 弓网系统的稳定性与鲁棒性得到提高.
| 表 8 接触网压力与弓头位移的波动参数对比 |
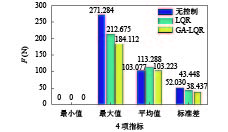
由表5(v2数据)、表6、表7绘制3种方法的对比效果图如图13、图14所示. 根据柱状图对比分析, 可知将LQR主动控制器用于弓网系统, 减小了曲线的波动范围, 有效地提高了系统的稳定性和鲁棒性, GA-LQR主动控制器比LQR主动控制器更加有效地抑制了接触压力和弓头位移的波动范围, 说明GA-LQR比LQR主动控制器的动态性能和鲁棒性更好.
|
图 13 200 km/h时基于3种方法的接触压力对比 |

|
图 14 200 km/h时基于3种方法的弓头位移对比 |
4 结论
本文以受电弓为控制研究对象, 利用三元质量模型建立弓网系统的动力学模型, 设计基于GA算法优化的LQR主动控制器, 通过仿真数据对比分析, 经过优化的LQR主动控制器能够很大程度地降低弓网系统中接触压力和弓头位移的波动, 提高了系统的动态性能和鲁棒性, 极大程度地降低了弓网的离线率, 提高了高速列车的受流质量.
| [1] |
鲁小兵, 刘志刚, 宋洋, 等. 受电弓主动控制综述. 交通运输工程学报, 2014, 14(2): 49-61. |
| [2] |
刘金亨, 陈今润, 吕郁青, 等. 基于LQR的一阶直线双倒立摆最优控制系统研究. 自动化技术与应用, 2009, 28(5): 11-13. |
| [3] |
杨志波, 罗鹏飞, 刘凯飞. 基于有限元的发动机连杆优化设计. 河南理工大学学报(自然科学版), 2013, 32(1): 65-68. |
| [4] |
李玉东, 李青, 李辉. 双变量交-交变频器调速量化控制算法研究. 河南理工大学学报(自然科学版), 2012, 31(2): 196-200. |
| [5] |
武俊峰, 张继段. 两轮自平衡机器人的LQR改进控制. 哈尔滨理工大学学报, 2012, 17(6): 1-5. |
| [6] |
谭文龙. 一种改进的二级倒立摆LQR控制器参数优化方法. 重庆理工大学学报(自然科学), 2012, 26(3): 85-88, 108. |
| [7] |
鲁小兵, 刘志刚. 高速铁路受电弓主动控制算法适用性研究. 西南交通大学学报, 2015, 50(2): 233-240. |
| [8] |
罗庆, 黄民翔, 郭雨涵. 基于模糊PID主动控制的仿真及应用. 电气传动, 2015, 45(8): 36-40. |
| [9] |
郭京波, 杨绍普, 高国生. 变刚度弓网系统主动控制研究. 振动与冲击, 2005, 24(2): 9-11, 15. |
| [10] |
时光, 陈忠华, 郭凤仪, 等. 弓网接触力反馈线性化控制. 控制理论与应用, 2016, 33(1): 85-91. |
| [11] |
杨岗, 李芾. 基于LQR的高速受电弓最优半主动控制研究. 铁道学报, 2011, 33(11): 34-40. |
| [12] |
庄哲, 施莹, 彭飞, 等. 受电弓状态反馈线性化主动控制方法研究. 机械科学与技术, 2017, 36(10): 1604-1610. |
| [13] |
张进秋, 彭虎, 张建, 等. 车辆悬挂LQR主动控制权矩阵权重参数优化. 振动与冲击, 2018, 37(22): 214-219. |
| [14] |
杨凌霄, 李晓阳. 基于GA的两轮自平衡小车LQR最优控制器设计. 河南理工大学学报(自然科学版), 2015, 34(1): 85-90. |
| [15] |
宋雪健, 郑宾, 陈晔, 等. 基于多种群遗传算法的LQR振动主动控制研究. 科学技术与工程, 2016, 16(29): 103-109. |
 2020, Vol. 29
2020, Vol. 29



