2. 中国科学院 软件研究所, 北京 100190;
3. 中国科学院大学, 北京 100049;
4. 中国科学院 沈阳计算技术研究所, 沈阳 110168;
5. 山东大学 大数据技术与认知智能实验室, 济南 250000;
6. 北京市中关村中学, 北京 100086
2. Institute of Software, Chinese Academy of Sciences, Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China;
5. Big Data Technology and Cognitive Intelligence Laboratory, Shandong University, Jinan 250000, China;
6. Zhongguancun Middle School of Beijing, Beijing 100086, China
排课问题是一个组合优化问题, 20世纪60年代初, Gotlieb提出了一个关于课程表, 并使用算法求解了三维线性规划问题. 在这之后, 学术界对这一问题展开了逐步深入的讨论, 讨论关注在求解方法的复杂度及问题是否一定存在解这两方面. 20世纪60年代中期, Mihoc和Balas把求解课程表的数学表达式转化为了一个优化问题[1], 之后有学者在排课的各种变量之间建立线性编程. 有部分学者使用遗传算法[2,3]来解决这一类问题. 遗传算法是模拟达尔文进化论自然选择的思想, 是一种优胜劣汰的算法, 适应环境能力差的个体, 随着时间会被淘汰, 剩下总群中的个体都是适应环境的个体[4]. 有些学者基于遗传算法做了一些优化工作, 如使用两次遗传算法分别对学生分组和排课[5], 排课中将每个年级的班级分为若干个组再进行排课[6], 基于模式的改进遗传算法[7], 二元变异算子代替传统的变异算子[8], 结合水平集概念优化遗传算法[9], 引入新的交叉算子及替换操作[10], 提出退化混沌突变算子进行优化[11], 使用遗传算法和其他算法组合的方式对排课问题进行求解[12,13]等.
这些探索使得遗传算法在解决排课问题上, 具有针对课表迭代过程中早熟收敛或停滞找不到解的问题, 存在使解有可能达到全局最优的优势. 但同时存在收敛速度慢, 迭代过程中产生很多无用解的问题. 并且更多的是融合其他算法或对遗传算法已有算子进行改进.
新课改走班制的推行, 实现了学生的自主选科选课. 大多数省份规定从物化生史地政6门科目中学生选择自己擅长的科目作为高考科目[14,15], 有的省份还会多一门信息技术科目, 有些省份还会出限选科目套餐, 只能在规定的科目套餐里选择科目. 允许学生自己选择科目, 意味着学校需要根据每个科目的选择人数对每个科目中的学生进行分班, 再加上教师、教室、上课时间等多类软硬件资源的约束, 师、生、学校获得一套可行课表成为一个新的典型的具有高复杂度的组合优化问题.
针对新课改实行的走班制排课, 本文把冲突染色体算子引入到遗传算法中, 提出冲突染色体算子优化在使用遗传算法解决走班制排课难题中存在的算法迭代过程中收敛速度慢的问题. 冲突染色体可以剪掉算法迭代过程中产生的无用解, 采用冲突染色体优化的遗传算法既可以保留遗传算法本身解的搜索能力, 又可以加速算法收敛, 从而减少走班制排课所需时间, 提升了走班制排课的效率. 并依据此优化算法及多种分班策略、集成的其他数据模块构建了一套新的走班制排课系统用于验证此优化算法的有效性.
2 走班制排课问题走班制教学前的排课按照行政班模式, 不涉及学生选课问题. 其排课时不需考虑学生自主选择的课程造成的影响, 排课的难度相对走班制排课要低, 走班制排课与传统行政班排课最大的区别在于是否考虑学生上课冲突问题.
走班排课过程中需考虑如何衡量排课算法的优劣其实来源于排课算法的核心问题, 那就是如何对学生、教师、时间、教室、课程等教育资源的组合与规划[16], 这种规划必须是建立在各个资源没有冲突且它们都能发挥出本身优势之上.
2.1 问题分析学校硬件和软件资源是否充裕, 也直接影响着排课算法的结果, 如是否对学生选课有限制, 教师是否充裕, 教室是否充裕等. 还有一些中学对学生分班有特殊要求, 如各班级成绩要均匀; 根据学生成绩还要做分层, 学习较快的同学进入快班, 学习较慢的同学进入慢班等.
根据学生选课情况分班是排课的第一步, 班级分的好对后期算法快速迭代效果明显, 冲突率也较低. 班级分不好也可能排不出课表. 学生分班后对其配备教师和课时. 把课程、学生、教师绑定在一起, 即每一门课程都包含一个班的学生和一个教师. 再把课程和上课时间、上课教室组合找出一个满足要求的课表.
以上是一款排课算法应满足的最基础要求, 一款好的排课算法还应尽可能多的满足学校提出的各种软性要求, 如教案齐头, 某个教师某天某节课不能排课等等, 排课总用时也应尽可能少.
为解决以上问题, 提出以冲突染色体算子为核心的遗传算法优化策略, 并以实验和系统验证该优化策略的有效性.
3 优化遗传算法 3.1 数学模型走班制排课问题很容易忽略的一点是学生如何分班, 排课前要根据学生的选课情况进行分班, 分班策略做的不好, 排课时遇到冲突的概率就会大大增加, 导致排不出课表. 学生选好课后, 由教务老师负责按各科目分班, 算法模型实现了按学生科目成绩、随机、学生选课组合等分班策略, 满足学校对分班的多需求, 其中按选课组合分班可大程度降低排课过程中学排课冲突.
某个班的学生定义如下, n为此班级的人数:
| $S=\left\{ {{s_0},{s_1},\cdots,{s_n}} \right\}$ | (1) |
老师集合定义如下, j为教师总数:
| $T=\left\{ {{t_0},{t_1},\cdots,{t_j}} \right\}$ | (2) |
所有班级的集定义如下, k为班级总数, 包含行政班班级和教学班班级:
| $C=\left\{ {{c_0},{c_1},\cdots,{c_k}} \right\}$ | (3) |
所有课程的集合定义如下, p表示所有课程总数:
| $L=\left\{ {{l_0},{l_1},\cdots,{l_p}} \right\}$ | (4) |
所有教室的集合定义如下, m表示教室总数:
| $R=\left\{ {{r_0},{r_1},\cdots,{r_m}} \right\}$ | (5) |
所有课位的集合表示如下, i表示课位总数:
| $ P = \left\{ {{p_0},{p_1},\cdots,{p_i}} \right\} $ | (6) |
则可使用如下五元组数据表示走班排课问题, 五元组表示如下:
| $f: < C,T,L,R,P > $ | (7) |
如选考班或行政班则表示为: 物理选考1班或数学1班, 由张三老师任课, 在高中楼103上课, 上课时间为周一第3节课
引入集合V: 绑定教师、学生、课程的事件信息的集合.
| $V=\left\{ {{v_0},{v_1},\cdots,{v_q}} \right\}$ | (8) |
| $ {v_i}={\rm{}}\left\langle {l,t,A} \right\rangle ,A \subseteq S $ | (9) |
式中, A可表示行政班或教学班学生集合. 则排课问题由五元组转换成三元组表示:
| $f: < V,R,P > $ | (10) |
假设一个课程v一周有N个课时. 每门课多少课时, 由学校教务老师定义, 则所有课时和有限的教室
| $R=\left\{ {{r_1},{r_2},\cdots,{r_i}} \right\}$ | (11) |
上课时间, “ti”表示周几, 第几节课等资源组合, 找出一个实现任一必须满足的约束和尽努力满足的软性约束的课表.
| $T=\left\{ {{t_1},{t_2},\cdots,{t_i}} \right\}$ | (12) |
总课表表示为:
| $X=\left\{ {{x_0},{x_1},\cdots,{x_q}} \right\}=\left\{ \begin{array}{c} \left\langle {{v_0},{r_i},{p_j}} \right\rangle \\ \left\langle {{v_1},{r_m},{p_n}} \right\rangle \\ \ldots \\ \left\langle {{v_q},{r_k},{p_s}} \right\rangle \\ \end{array} \right\}$ | (13) |
根据以上定义, 则可得出排课程表中必须满足的规则如下:
(1)同时间老师不能教两门课程
| ${f_1}\left( X \right)=\frac{{\displaystyle\mathop \sum \nolimits_{i=0}^q \displaystyle\mathop \sum \nolimits_{j=0}^q T}}{2}$ | (14) |
| $T=\left\{ {\begin{split} & {1,\;{l_i} \ne {l_j},{p_i}={p_j},{t_i}={t_j}} \\ & {0,\;{\rm else}} \end{split}} \right.$ | (15) |
(2)同时间学生不能排两门课程
| ${f_2}\left( X \right)=\frac{{\displaystyle\mathop \sum \nolimits_{i=0}^q \displaystyle\mathop \sum \nolimits_{j=0}^q T}}{2}$ | (16) |
| $T=\left\{ {\begin{split} & {1,\;{l_i} \ne {l_j},{p_i}={p_j},{s_i}={s_j}} \\ & {0,\;{\rm else}} \end{split}} \right.$ | (17) |
(3)同时间同教室不安排两门课程
| $ {f_3}\left( X \right)=\frac{{\displaystyle\mathop \sum \nolimits_{i=0}^q \displaystyle\mathop \sum \nolimits_{j=0}^q T}}{2} $ | (18) |
| $ T=\left\{ {\begin{split} & {1,\;{l_i} \ne {l_j},{p_i}={p_j},{r_i}={r_j}} \\ & {0,\;{\rm else}} \end{split}} \right. $ | (19) |
以及考虑课表可用性, 还需满足以下约束.
(4)课时均匀: 当某个课程有多个课时, 一周内其课时应该均匀分布到每一天.
| ${g_1}\left( X \right)=\frac{{\displaystyle\mathop \sum \nolimits_{i=0}^p T}}{2}$ | (20) |
| $ {\rm{}}T=\left\{ {\begin{split} &{0,\;{\text{满足}}S{\text{条件时}}}\\ &{1,\;{\rm else}} \end{split}} \right. $ | (21) |
| $ S:\left\{ {\begin{split} &{0 \le \displaystyle\mathop \sum \limits_{\alpha =0}^8 {B_{ij}} \le 1,\lambda \le 5}\\ &{\displaystyle\mathop \sum \limits_{\alpha =0}^8 {B_{ij}} \ge 1,\lambda > 5} \end{split}} \right. $ | (22) |
| $ {B_{ij}}=\left\{ {\begin{split} &{1,\;{\text{有课}}}\\ &{0,\;{\text{无课}}} \end{split}} \right. $ | (23) |
(5)课时连排: 某些课程有连着排需求, 如语文课周五上午排在第2节和第3节课, 用于写作文.
| ${g_2}\left( X \right)=\frac{{\displaystyle\mathop \sum \nolimits_{i=0}^p T}}{2}$ | (24) |
| $ T=\left\{ {\begin{split} &{0,\;{\text{满足}}S{\text{条件时}}}\\ &{1,\;{\rm else}} \end{split}} \right. $ | (25) |
| $S:\sum\nolimits_{\partial {\rm{=}}0}^8 {{B_{{\rm{ij}}}}=2} ,{j_2} - {j_1}=1,i \in [0,4]$ | (26) |
(6)教案齐头: 若一个教师带两个班, 则要求两个班的进度要相同.
(7)教师禁止或必须排课时间: 教师进修或者有其他原因, 需要设置教师禁止排课时间或必须排课时间.
在某个时间点是否允许排课表示如下, i是星期, j是课节:
| $ {{{B}}_{{{ij}}}}=\left\{ {\begin{split} &{1,\;{\text{必须排课}}}\\ &{0,\;{\text{禁止排课}}} \end{split}} \right. $ | (27) |
在算法迭代过程中, 算法的目标函数
| $ {\rm{\varphi }}\left( X \right)={\rm{}}\dfrac{{\dfrac{1}{{F\left( X \right) + 1}} + \frac{1}{{G{{\left( X \right)}^2} + 1}}}}{2} $ | (28) |
| $ {\rm{\varphi }}\left( X \right) \in \left( {0,1} \right] $ | (29) |
| ${{F}}\left( X \right)={f_1}\left( {{x}} \right) + {f_2}\left( {{x}} \right) + {{{f}}_3}\left( {{x}} \right)$ | (30) |
| ${{G}}\left( X \right)={{{g}}_1}\left( {{x}} \right) + {{{g}}_2}\left( {{x}} \right) + {{{g}}_3}\left( {{x}} \right) + {{{g}}_4}\left( {{x}} \right)$ | (31) |
其中, F(X)和G(X)表示当前课表必须满足的约束冲突数. 个体在当前排课方案中每违背一次约束条件, F(X)或G(X)值就加1. 当
在使用相同计算硬件资源条件下, 加入了以下优化策略, 排课效率提升了19.2%.
(1)变异率实现自缩放
遗传算法可以设置初始交叉率和变异率, 每次交叉或者变异时都会按照预先设定好的值进行, 但随着迭代的进行, 考虑到每个个体对变异的需求不同, 变异率若可动态调整, 则可使迭代速度加快.
课表在编译时的变异率adaptiveMutationRate做了以下优化: bestFitness为当前代中适应度最好的课表的适应度; individual表示某一代中的某个课表; population表示某一代所有的课表集合.
Opt1=bestFitness - individual.getFitness()
Opt2=bestFitness - population.getAvgFitness()
Opt1表示当前代课表中最好适应度与当前代中某个课表适应度之间的差值, Opt2表示当前代中某个课表与当前代课表中最好适应度之间的差值. adaptiveMutationRate作为新的变异率参与迭代计算.
adaptiveMutationRate=(Opt1 / Opt2)*mutationRate Opt1/ Opt2的比值作为原变异率的膨胀系数.
(2)冲突染色体算子
冲突染色体算子是指构建长度与原有染色体一致的冲突染色体, 并对原有染色体进行冲突基因记录的过程.
冲突染色体结构如图1所示. 上方每一小格表示某一门课的1个课时, 小格内有两位数字, 第一位表示教室编码, 第二位表示课位编码.

|
图 1 冲突染色体 |
下方每位对应的0或1数字表示当前小格组合是否与其他组合存在冲突, 若冲突, 迭代时上方小格的值必改变, 从而保证课表中的冲突个数是在不断降低的, 如前面提到的硬性约束不满足, 利用此结构可剪掉算法求解过程中的无用解.
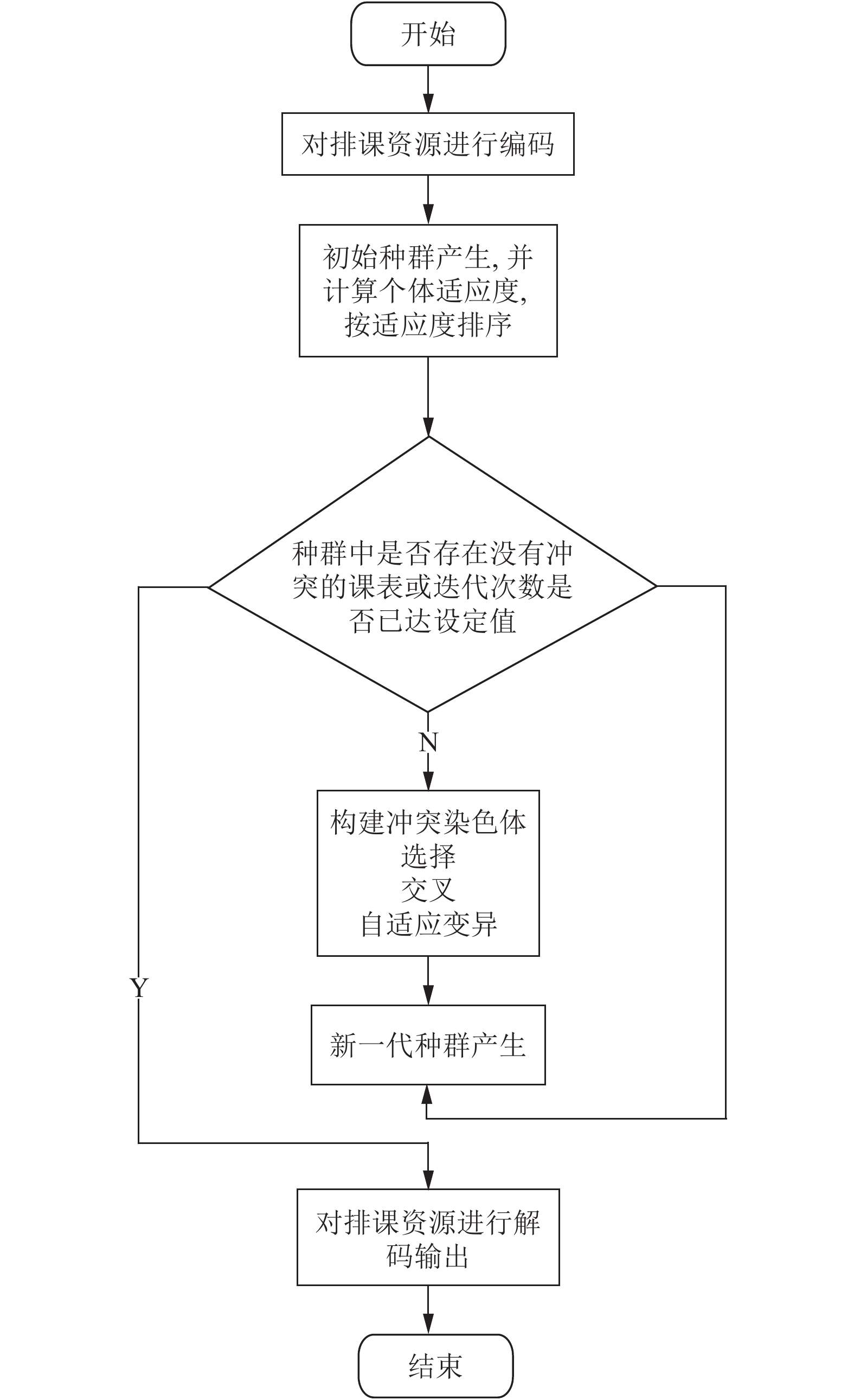
优化后的GA*算法流程如图2所示.
基本的步骤如下:
步骤1. 随机初始一个大小为N的课表种群M.
步骤2. 计算M中各个个体的适应度值, 根据适应度值的大小按照降序排序. 若个体最大适应度为1或迭代次数超过设置最大值转至步骤6.
步骤3. 生成一个大小为N的冲突染色体总群P, P中每个个体长度与M中每个个体长度一致, 初始化P中所有个体各基因为0, 表示基因没有冲突, 计算M中各个体冲突基因的下标, 并把P中这些下标对应位置的值赋为1, 表示此处基因存在冲突.
步骤4. 选择M中排名前k的个体直接继承到下一代.
步骤5. 对种群M进行选择交叉和自适应变异操作, 其中交叉和自适应变异过程需要考虑个体对应的冲突染色体, 存在冲突的基因, 不遵循交叉率和变异率规律, 此处基因100%交叉或者变异. 生成新的种群, 转到步骤2.
步骤6. 退出循环, 将结果解码输出课表.
|
图 2 GA* 算法流程图 |
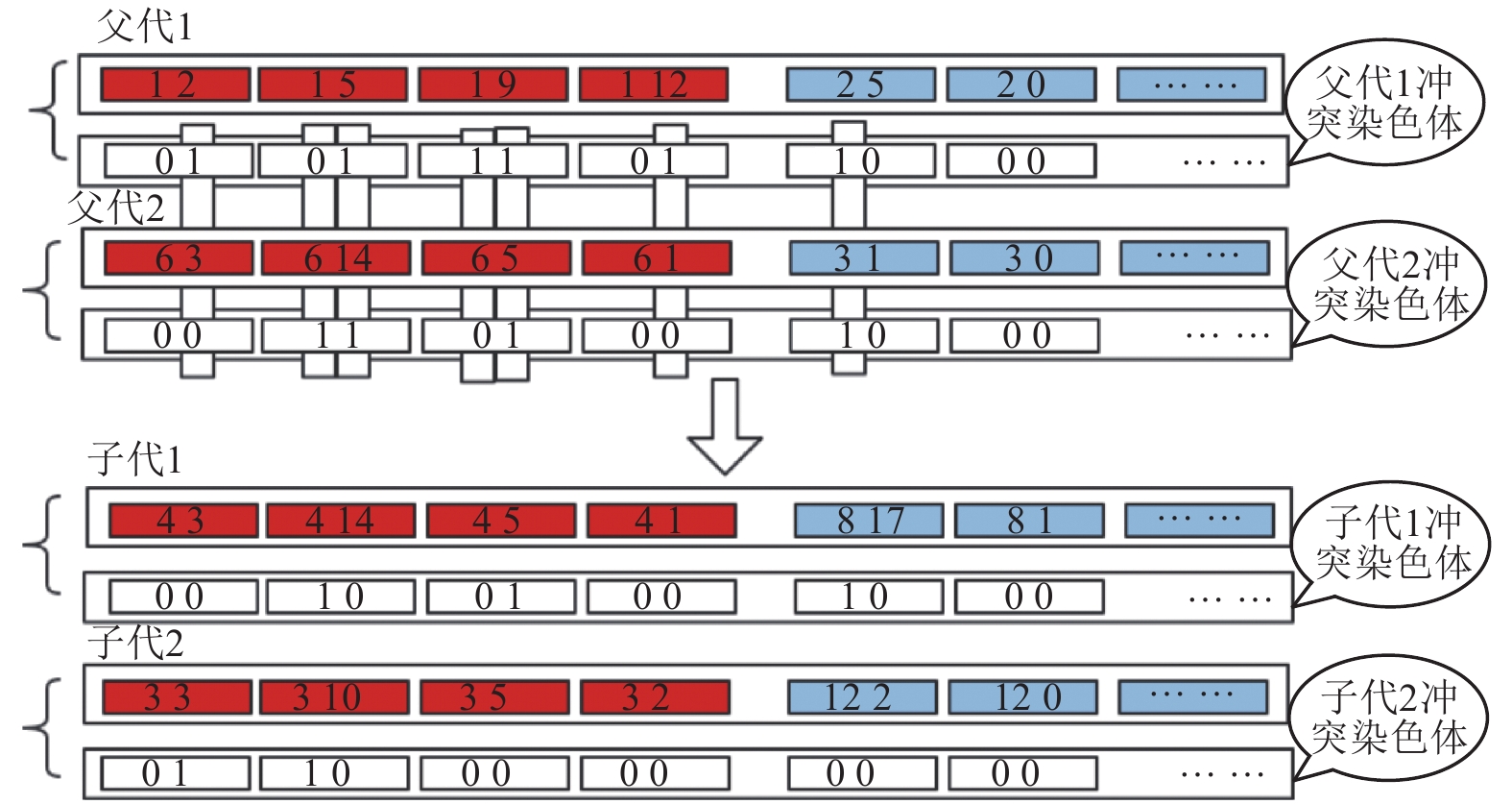
对算法迭代过程中优化的核心内容展开, 如图3.
|
图 3 冲突染色体作用图 |
可以看到新一代个体的冲突个数整体上是下降的, 证明算法的优化是有效的. 冲突染色体值为1的基因在变异过程时保证100%变异, 冲突染色体值为0的基因, 按自适应变异率变异.
4 实验构建与系统实现 4.1 数据来源本次实验使用某市某中学高二上学期真实走班选课数据, 包括495名学生, 31个教师, 18个教室, 12门课及学生的选课结果. 对比此优化算法. 实验以排课时间作为优化后的遗传算法的评价指标, 以分班时间及排课时间验证分班策略对走班排课的影响, 都以秒为单位. 各个科目的选课人数如表1所示.
| 表 1 走班课程选课结果 |
由表1可以看出, 物理选择人数是最多的, 接近一半学生选择此科目作为选考科目, 因为有些高校已经发布专业录取条件, 如要求选择报考计算机专业时高中必须把物理作为选考科目.
4.2 实验及结果分析实验使用的是某中学服务器, 其服务器配置如表2.
| 表 2 服务器配置 |
3种分班策略分别为随机分班、按照成绩分班、按照选课组合分班. 随机分班指不考虑任何条件, 随机的把选择某个科目的学生分到某个班. 按照成绩分班指考虑学生当前科目的成绩, 按照排名前后分入某个班级. 按照选择组合分班指把选择相同3个科目的学生分到同一个班. 在前文数据模型中多约束条件下走班制排课对比效果如表3所示.
表3中值为每种策略各运行3次, 求平均值所得. 通过分班时间可以得出, 随机分班所花时间最少, 按成绩分班由于需要考虑每个学生的成绩及排名, 花费时间最多.
| 表 3 算法优化后的排课效率对比 |
通过表3还可以看出, 在不同分班策略下, 优化后的GA*算法排课时间都明显下降, 并且按照选课组合分班排课时间花费最少, 为101 s, 因为走班排课问题中最容易引发冲突的点是学生, 按照选课组合分班, 可以降低学生的排课冲突. 因此证明使用该冲突染色体算子优化可以提高排课效率.
4.3 系统实现面向中学的教师或学生等用户时, 一个完整的走班制排课系统应满足从选课、分班到排课等完整的流程. 新系统对整体排课流程进行了梳理, 并集成学生选课、学生成绩、学生评测等模块.
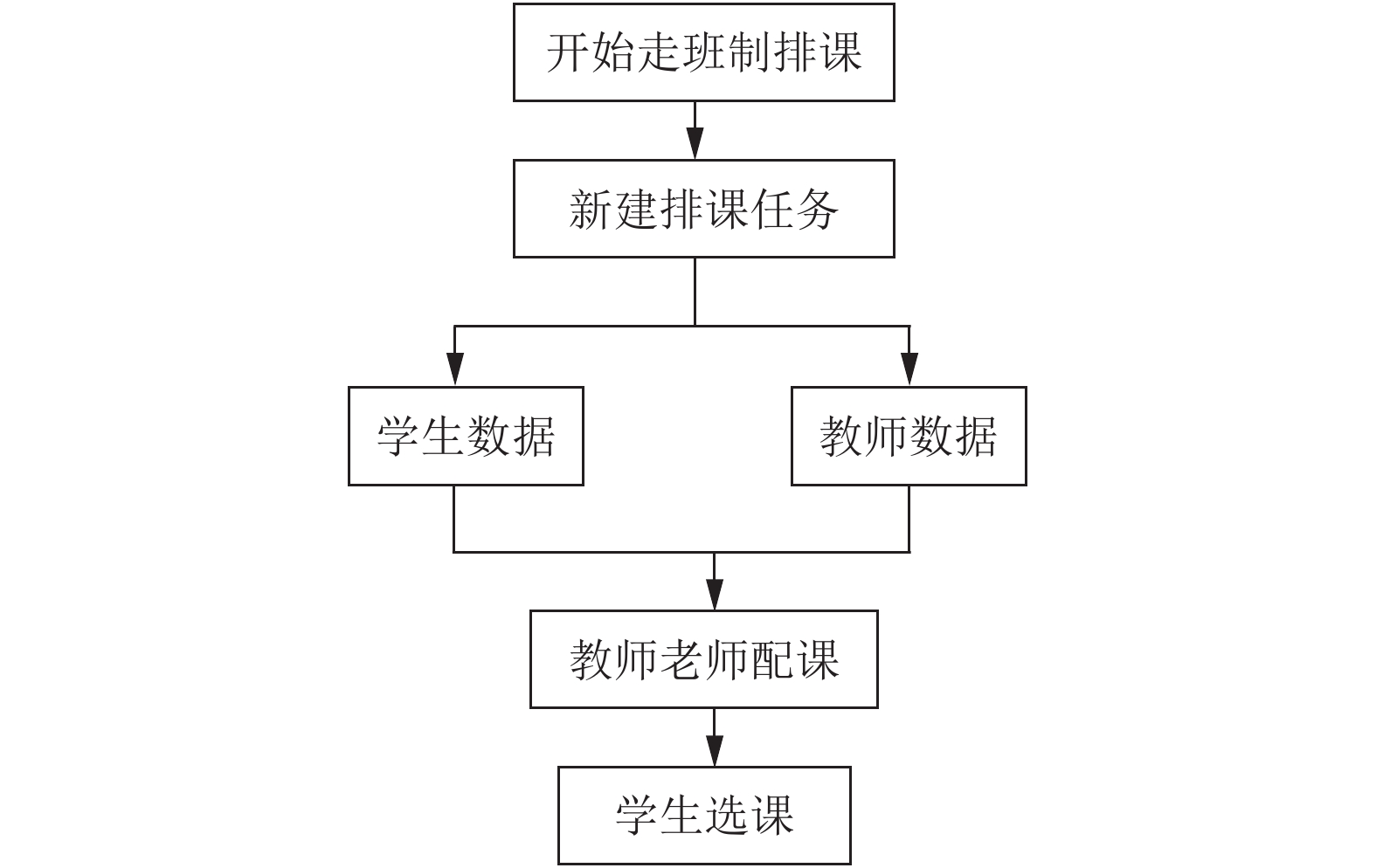
首先教务老师新建排课任务时, 首先选定年级和学期, 系统会自动获取对应年级的学生数据, 及教师数据. 新建排课任务完成以后, 开始对此次排课任务配置课程, 配置完成后, 学生登录系统可看到配置的课程数据, 并进行选择课程操作, 选择课程中后端会自动校验选择课程数据是否正确. 如图4所示.
|
图 4 新建排课任务 |
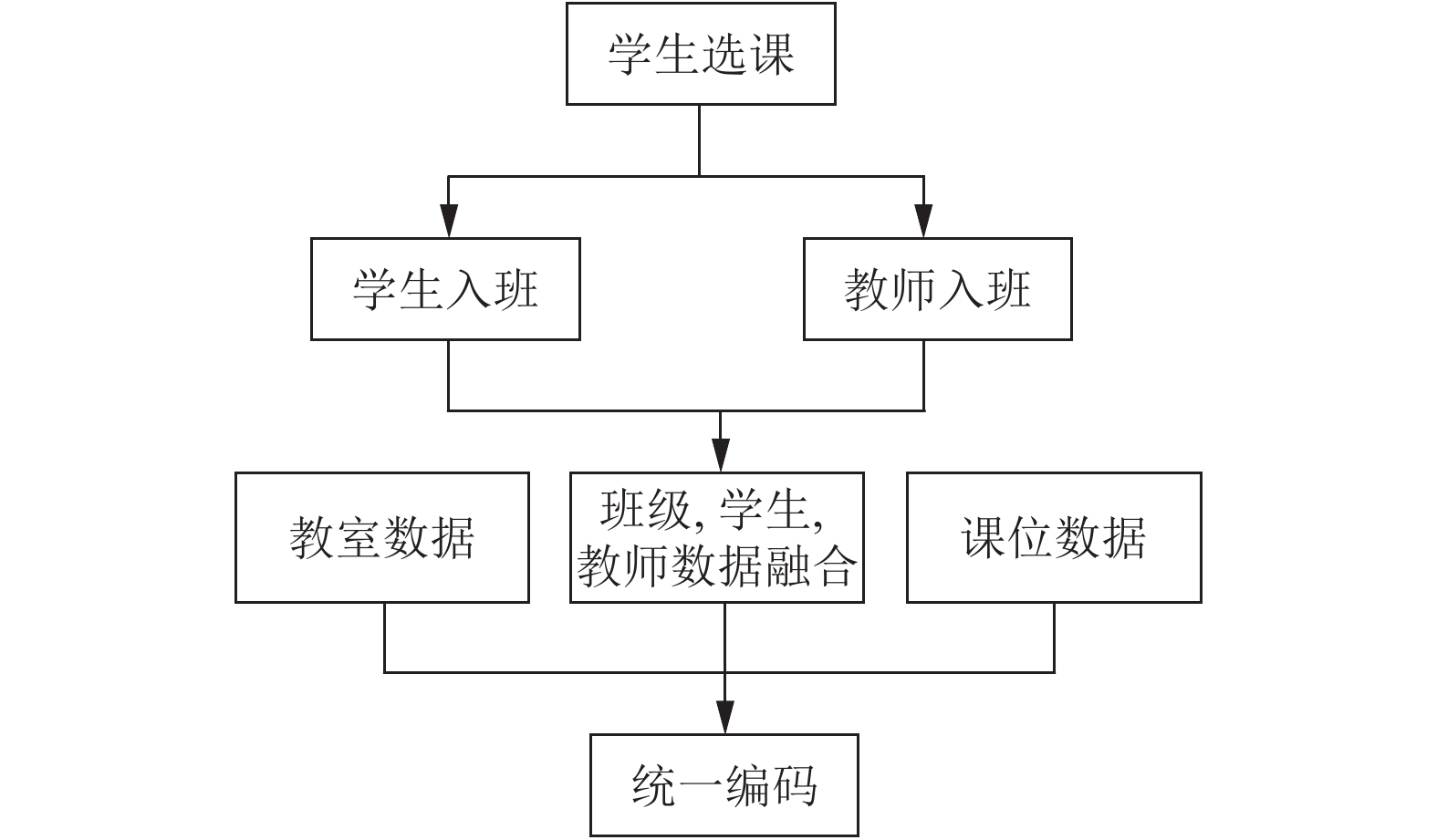
学生选课完成后, 教务老师根据学生选课情况, 调用学生成绩模块数据或学生评测模块数据等进行班级分配, 分配完成后学生即分入了确定班级, 再为这些班级分配教师. 此时课程、学生、教师数据完成融合. 具体样式如“物理选考1班, xx教师, 5课时, 学生列表{1. 学号; 2. 学号; …; 40. 学号}”. 如图5所示.
待以上操作全部完成后, 开始设置软约束条件, 将编码后的数据输入到优化的走班制排课算法中, 系统在迭代过程时会调用配置的软约束, 及默认必须满足的硬约束. 排课结束后课表解码并返回给用户.
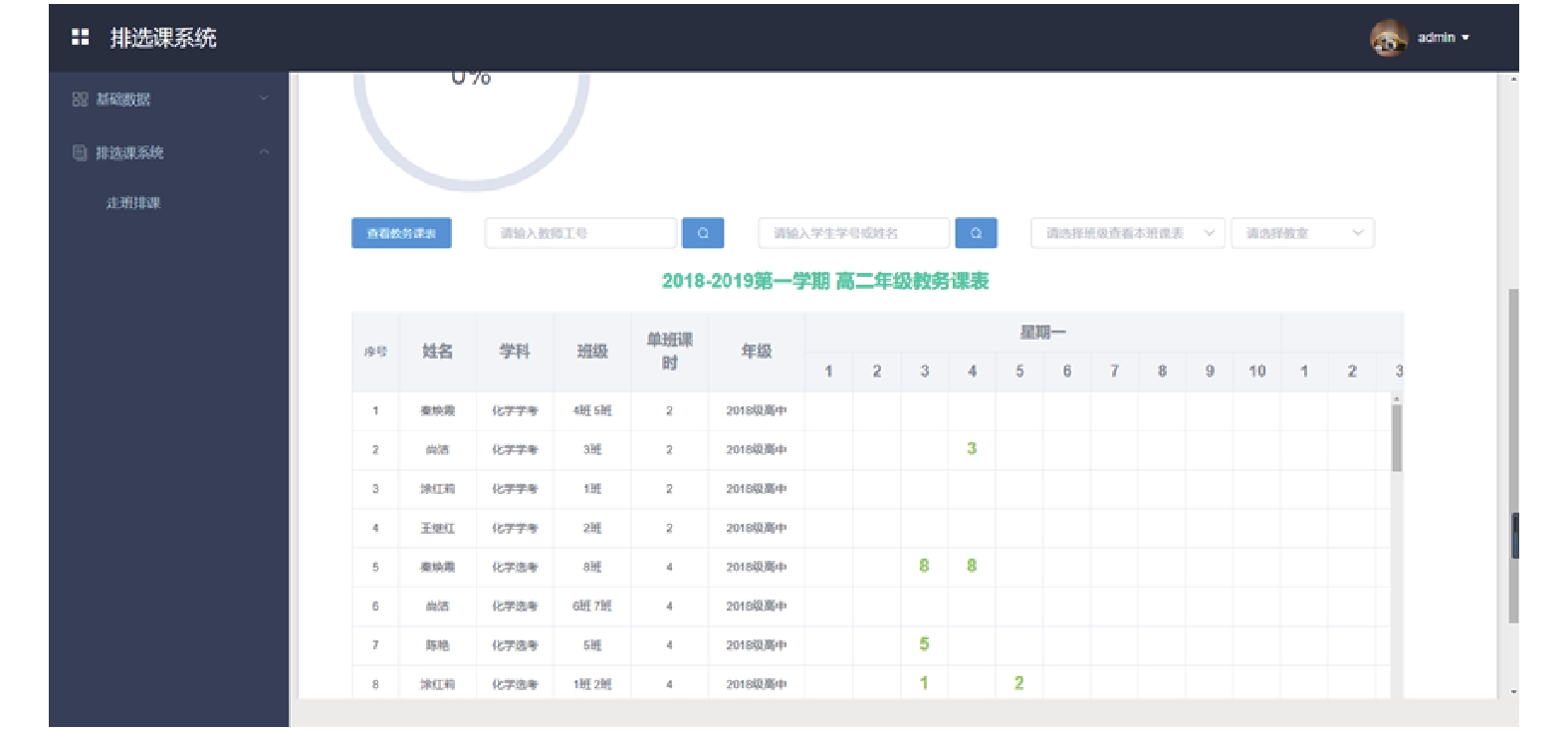
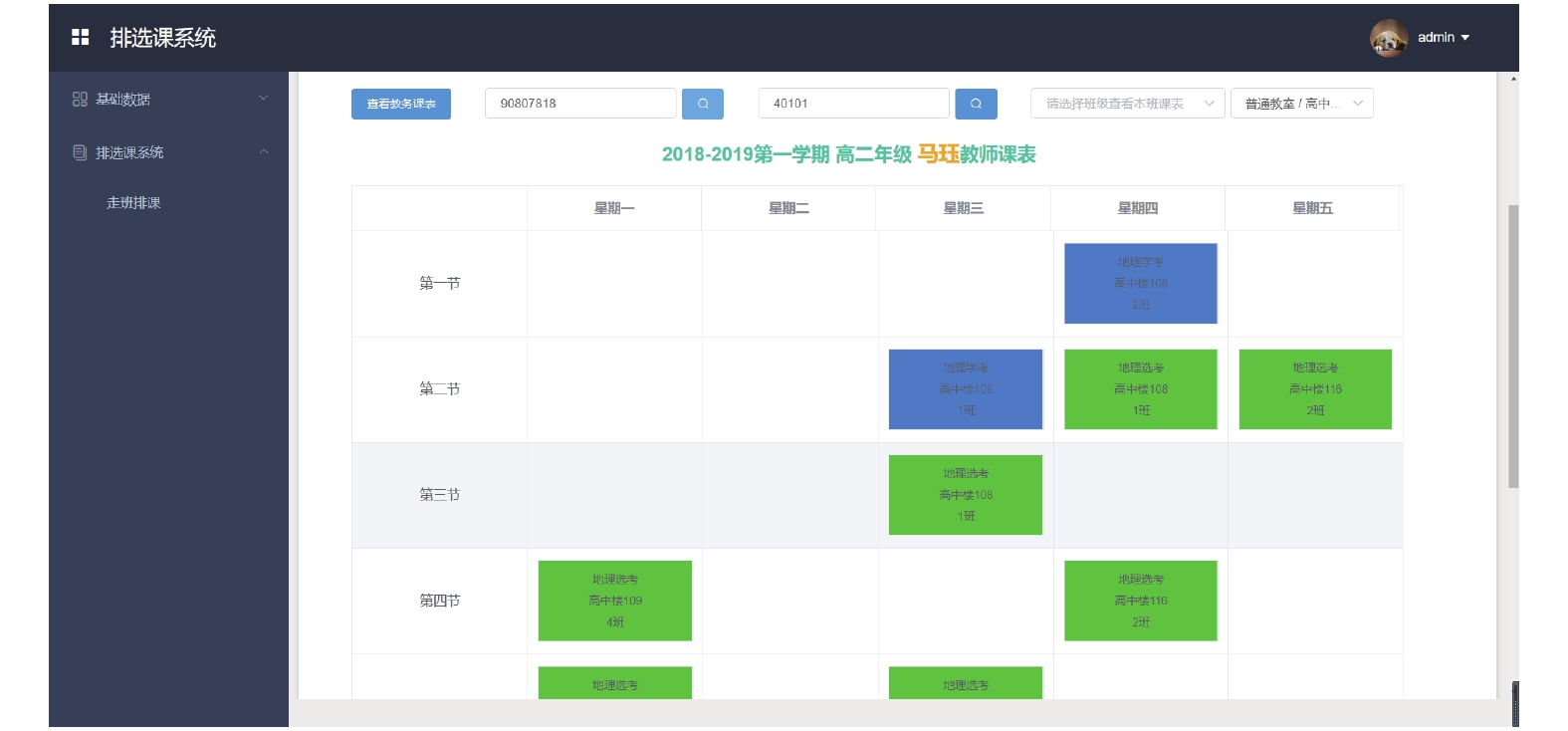
系统输出多种类型课表, 如教务课表、学生课表、教师课表、教室课表. 如图6、图7给出部分课表, 图6为教务部分课表, 图7为教师课表.
|
图 5 数据融合及编码 |
|
图 6 教务部分课表 |
|
图 7 教师课表 |
系统运行时间及结果进一步验证了冲突染色体优化的有效性.
5 结论与展望本文通过实验验证了冲突染色体算子优化遗传算法的有效性, 提高了走班制排课的效率. 为使用遗传算法解决组合优化问题提供了一种优化思路. 实验还验证了不同的分班策略对走班制排课的影响, 实验表明按照选课组合对学生进行分班, 同样算法条件下可使走班制排课效率得到更多的提升. 并依此构建了一个新走班制排课系统, 该系统目前正在某中学试运行, 并为高二年级进行了走班制排课, 反馈效果很好.
当前对采取走班制该教学方式的学校而言排课还是一个挑战, 考虑到约束条件多、动态性强, 且学校具有各自不同的走班需求, 使得算法实现的复杂度变高. 目前此算法实现了在当前约束条件下可排出课表的问题, 但也可能出现约束扩增到一定程度时算法可能无解的问题, 后续还需继续优化算法及对约束条件的分类梳理, 对比分析不同约束对排课的影响.
| [1] |
陶滔, 谢卫星. 课表模型及排课算法应用. 计算机系统应用, 2011, 20(2): 198-201. |
| [2] |
Alcaraz Soria J, Maroto Álvarez C. Genetic algorithms for the resource-constrained project scheduling problem. BEIO, Boletín de Estadística e Investigación Operativa, 2009, 25(1): 22-25. |
| [3] |
Saptarini NGAPH, Suasnawa IW, Ciptayani PI. Senior high school course scheduling using genetic algorithm. Journal of Physics: Conference Series, 2018, 953: 012067. DOI:10.1088/1742-6596/953/1/012067 |
| [4] |
吉根林. 遗传算法研究综述. 计算机应用与软件, 2004, 21(2): 69-73. |
| [5] |
王卫红, 李文琼. 基于改进遗传算法的高中走班制排课算法. 浙江工业大学学报, 2016, 44(6): 601-607, 670. |
| [6] |
陈璐, 王秀. 改进遗传算法求解走班制下的排课问题. 计算机工程与应用, 2019, 55(6): 218-224. |
| [7] |
欧阳森, 王建华, 宋政湘, 等. 一种新的改进遗传算法及其应用. 系统仿真学报, 2003, 15(8): 1066-1068, 1073. |
| [8] |
杨启文, 蒋静坪, 张国宏. 遗传算法优化速度的改进. 软件学报, 2001, 12(2): 270-275. |
| [9] |
李庆华, 杨世达, 阮幼林. 基于水平集的遗传算法优化的改进. 计算机研究与发展, 2006, 43(9): 1624-1629. |
| [10] |
宋莹莹, 王福林, 兰佳伟. 改进遗传算法在油茶果采摘机优化中的应用. 农机化研究, 2020, 42(6): 14-18. |
| [11] |
张春慨, 王亚英, 李霄峰, 等. 混沌在实数编码遗传算法中的应用. 上海交通大学学报, 2000, 34(12): 1658-1660. |
| [12] |
王俊丽. 基于改进的混合遗传算法的排课问题研究[硕士学位论文]. 大连: 大连海事大学, 2013.
|
| [13] |
许秀林, 胡克瑾. 基于约束满足和遗传算法的排课算法. 计算机工程, 2010, 36(14): 281-284. |
| [14] |
徐奇峰. 新课标下选考学科分层走班教学策略——以高中物理学科分层走班为例. 新课程(下), 2018(9): 8-9. |
| [15] |
王润, 周先进. 新高考改革背景下高中走班制机制构建. 当代教育科学, 2016(6): 49-53. |
| [16] |
吴小芳. 新高考走班制教学下的学校资源优化研究[硕士学位论文]. 上海: 华东师范大学, 2018.
|
 2020, Vol. 29
2020, Vol. 29



