在智能技术不断发展创新的今天, 智能家居受到了广泛关注和使用, 智能窗帘作为智能家居中必不可少的部分, 极大影响着室内生活环境和居家生活品质[1-3]. 除解放双手、感应开合外, 各种各样的拓展功能如防盗报警、远程控制等, 在很大程度满足了人们对极致生活的追求, 成为了居家生活不可或缺的好帮手.
目前市场上生产的智能窗帘在使用中仍存在较大弊端, 其反应、调节、控制的时间跨度较大, 整体的控制效果受天气等自然因素影响, 窗帘系统的抗干扰能力和稳定性也较差[4-8]. 因此, 找到一种更加智能化、自动化、灵敏化, 同时具有较强鲁棒性的方式来控制家用窗帘已经成为大势所趋.
基于此, 本文提出一种能够实时检测室内光照强度, 并依据人体最适宜的环境标准自动调节被控窗帘开合程度的新型智能锁光窗帘控制算法, 将模糊控制算法与模糊自适应控制算法相结合并应用到锁光系统中[9-13], 使其具有可实时调节窗帘位置、保证室内采光充足、调节速率快、自动控制等优点, 极具市场价值.
1 整体控制方案本文设计的智能锁光窗帘控制系统使用的主控芯片为STC32F1, 外接有电机运动控制、电机驱动、智能检测、液晶显示4个主要模块, 其整体功能框图如图1所示.

|
图 1 整体功能框图 |
图1中, 电机运控模块共有3种基础控制方式, 分别为定时控制, 锁光控制和远程控制. 其中, 定时控制可根据定时打开或关闭窗帘, 锁光控制可自动将室内光强锁定在最优状态, 远程控制可利用手机软件远程控制窗帘开闭. 本文将对基于双模糊控制的锁光控制方式的优化算法进行详细阐述.
2 光控系统模型构建假定室内宜居光照强度为
| $\left\{ {\begin{array}{l} {e_{\varphi} \left( t \right)=\varphi_{0 }- \varphi \left( t \right)} \\ {ec_{\varphi} \left( t \right)=e_{\varphi }\left( t \right) - e_{\varphi} \left( {t - 1} \right)} \end{array}} \right.$ | (1) |
改变直流电机的输入电压, 电机转速会随之产生规律性变化, 故选择调节
而当
图2为光控系统模型的执行机构. 可以看出, 通过改变
|
图 2 模型的执行机构 |
3 设计模糊控制器
图3所示为模糊控制系统的工作机理. 在模糊控制系统中, 传感器将采集到的物理量转换为连续的电信号, 由 A/D转换器将这种电信号变为精确的数字量, 同时与给定值进行比较, 得到偏差e输入到模糊控制器中. 偏差e经模糊化处理为模糊集合E, 根据既定规则对集合E进行模糊推理可得模糊控制量U, 解模糊后得精确输出u. 用D/A转换器将输出u转换为模拟量, 并通过相应的执行机构作用于被控对象, 使其准确快速地达到期望状态.

|
图 3 模糊控制流程 |
3.1 模糊控制器FC
设定室内最宜居光强为
| $\left\{ \begin{array}{l} {\varphi _0} = 200\;{\rm{lx}}\\ {\varphi _{\max }}\left( t \right) = 400\;{\rm{lx}}\\ {\varphi _{\min }}\left( t \right) = 0 \end{array} \right.$ | (2) |
将式(2)代入式(1), 则有:
| $\left\{ {\begin{array}{l} {e_{\varphi} \left( t \right) \in \left[ { - 200,200} \right]} \\ {ec_{\varphi} \left( t \right) \in \left[ { - 400,400} \right]} \end{array}} \right.$ | (3) |
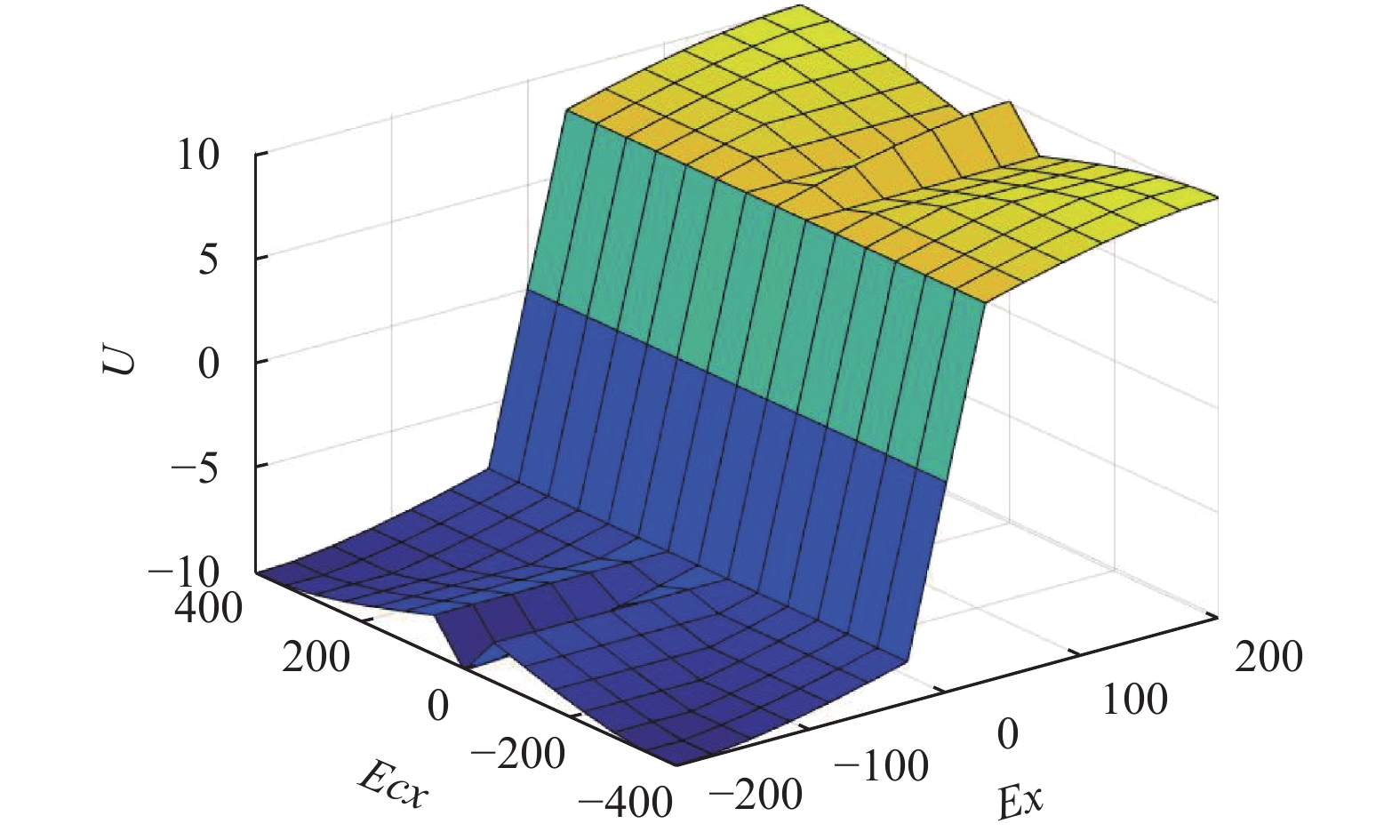
将
直流电机的电枢电压计算公式为:
| $U=C_{e} \phi n + I_{a} R_{a} + 2\vartriangle U_s$ | (4) |
式中,
将
|
图 4 控制器FC输入输出关系 |
3.2 模糊PID控制器F
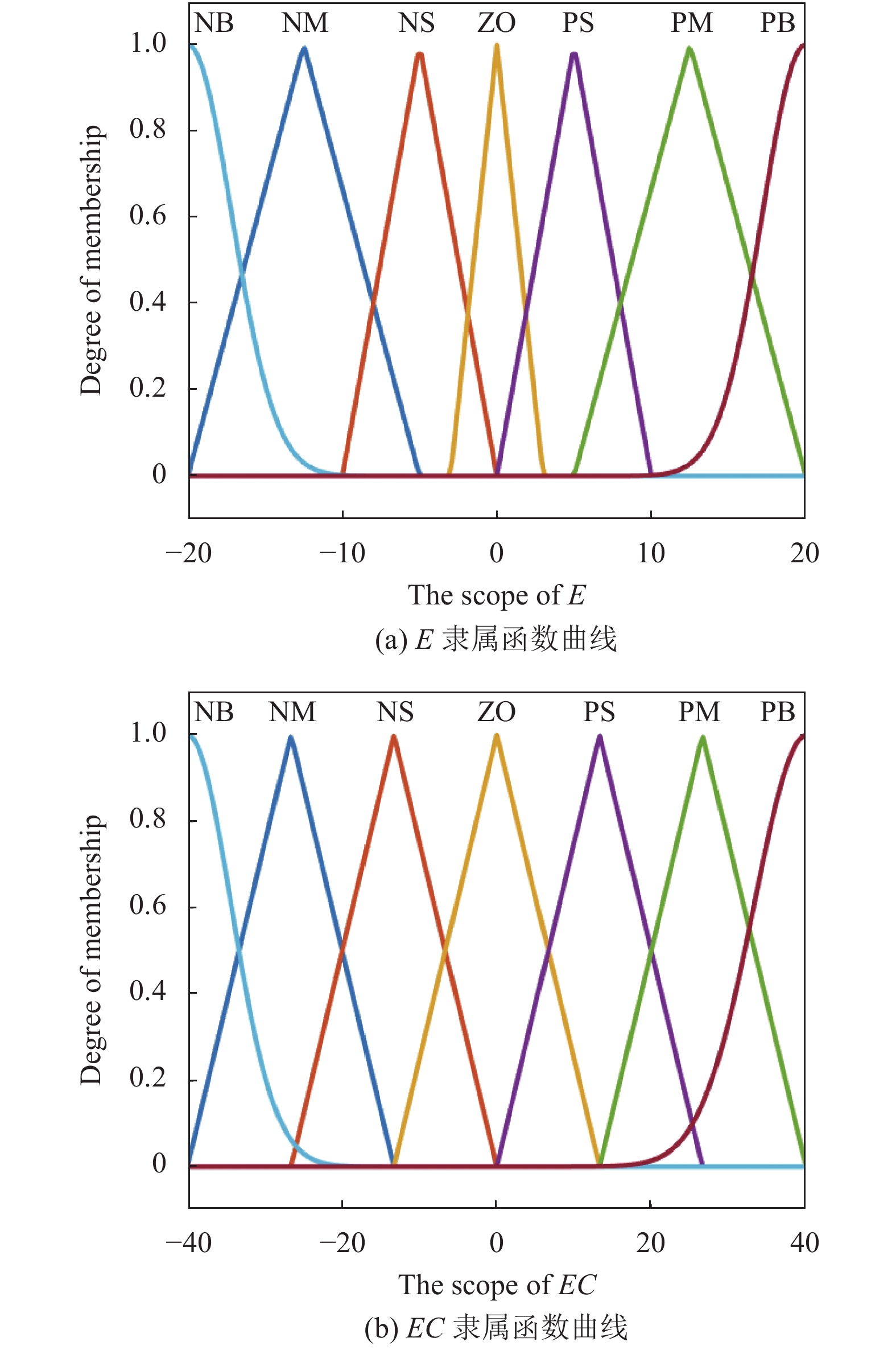
将
|
图 5 E、EC隶属函数曲线 |
输出为PID控制器3个参量Kp、Ki、Kd必要变化量的模糊量Kp、Ki、Kd, 且Kp、Ki、Kd={NB, NM, NS, ZO, PS, PM, PB}, 设置论域为[–3, 3]、[–1, 1]、[–0.05, 0.05]. 其隶属函数选择为三角函数.
在建立模糊规则时需要考虑到, E变大时向减小E的方向调节, E变小时保持系统稳定. 如在系统调节初期, 当实际值比标定值小很多且仍在不停的以远离标定值的方式变小的情况下, 为将实际值拉回, 必须大幅增加Kp以加快调节, 大幅减小Ki以使系统获得较快的动态响应, 同时适当增大Kd减少不必要的超调量. 上述描述可用模糊条件语句表示为 if E=NB and EC=NB then Kp=PB and Ki=NB andKd=PS. 表1~表3为控制器F具体的49条模糊规则.
| 表 1 Kp模糊控制规则表 |
| 表 2 Ki模糊控制规则表 |
| 表 3 Kd模糊控制规则表 |
4 搭建算法框架
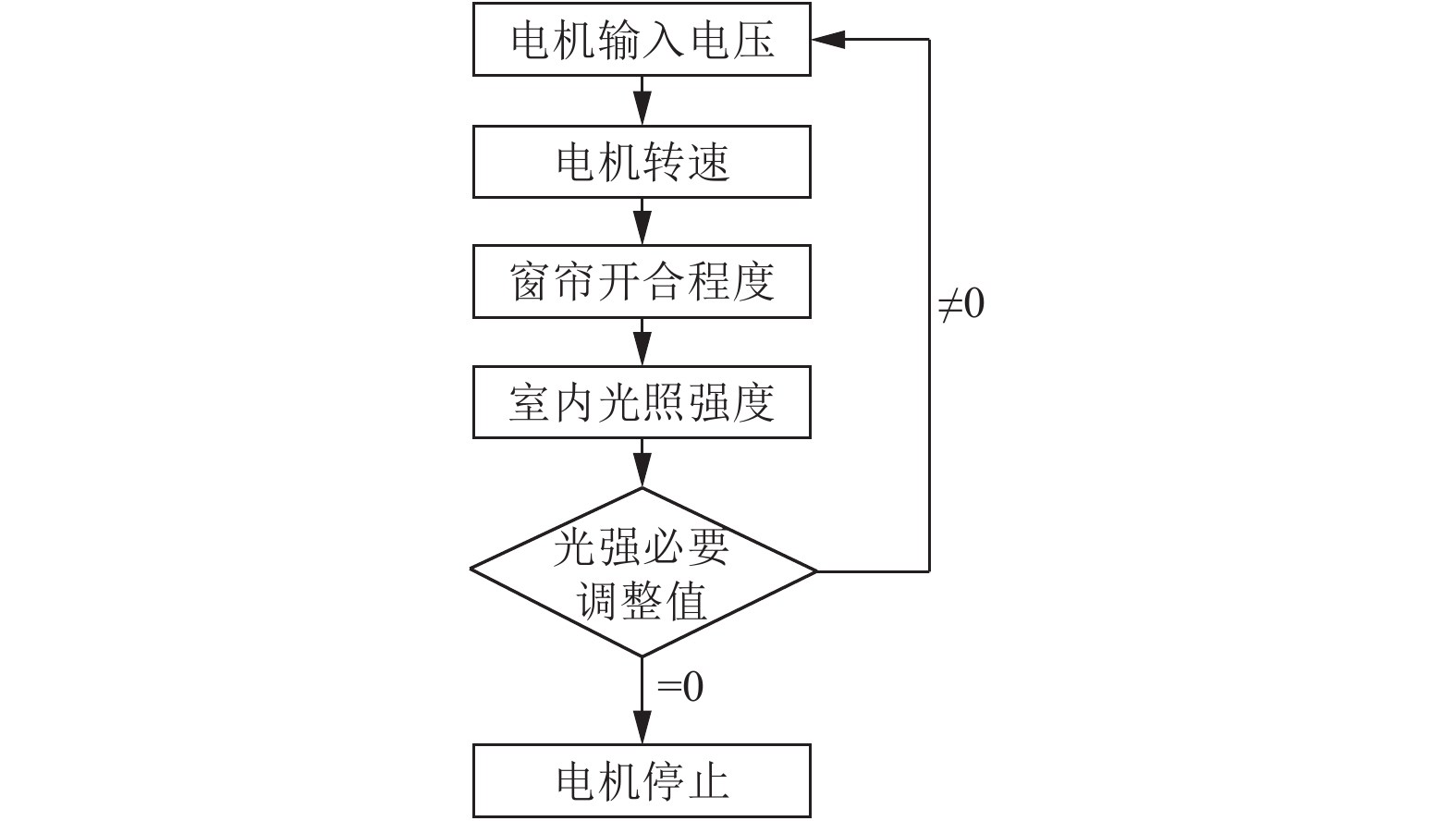
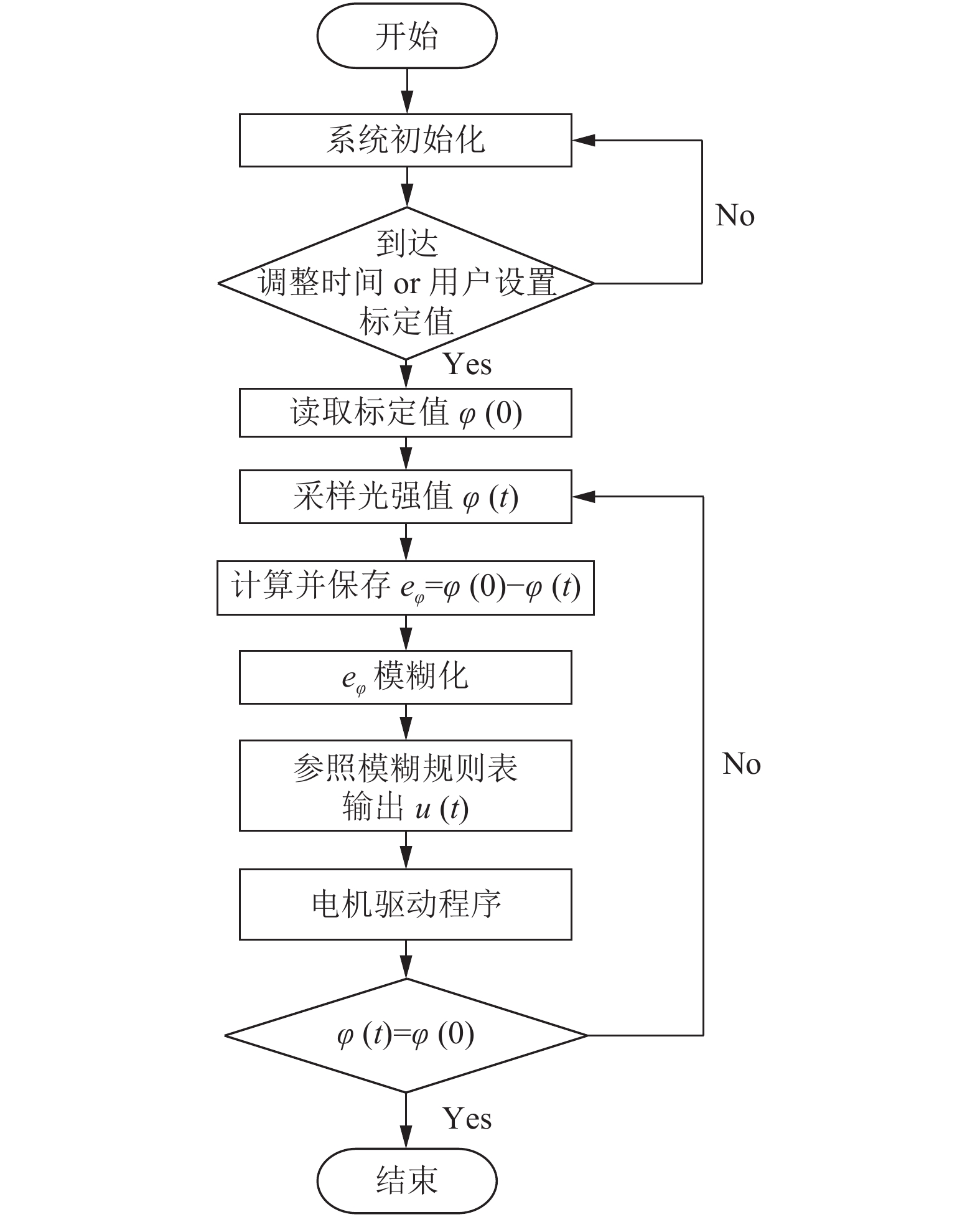
模糊控制器FC、F设计完成后, 将其与软件算法结合, 得到锁光控制方式的优化算法. 系统在接收到用户的设置信号或到达智能调整时间时, 将自动运行模糊算法进行控制系统中参数的自调整, 实现对室内光照强度的调节.
如图6, 将模糊规则表、输入输出论域与隶属函数写入STM32核心控制芯片的存储器中, 保证控制器在参数整定时可直接对模糊规则表进行寻址确定输出.
|
图 6 压控阶段算法 |
按照设定的采样频率
系统采集
直流电机的电压平衡方程为:
| $U - E=RI + L\frac{{{\rm d}I}}{{{\rm d}t}}=R\left( {I + T_l\frac{{{\rm d}I}}{{{\rm d}t}}} \right)$ | (5) |
式中,
| $\frac{{I\left( s \right)}}{{U\left( s \right) - E\left( s \right)}}=\frac{{{1 / R}}}{{T_{ls} + 1}}$ | (6) |
直流电机的转矩平衡方程为:
| $\left\{ {\begin{array}{l} {T_e - T_L = \dfrac{{G{D^2}}}{{375}}\dfrac{{{\rm{d}}n}}{{{\rm{d}}t}}}\\ {T_e = C_{m}I,T_L = C_m{I_L}} \end{array}} \right.$ | (7) |
式中,
| $\frac{{E\left( s \right)}}{{I\left( s \right) - {I_L}\left( s \right)}}=\frac{R}{{{T_m}s}}$ | (8) |
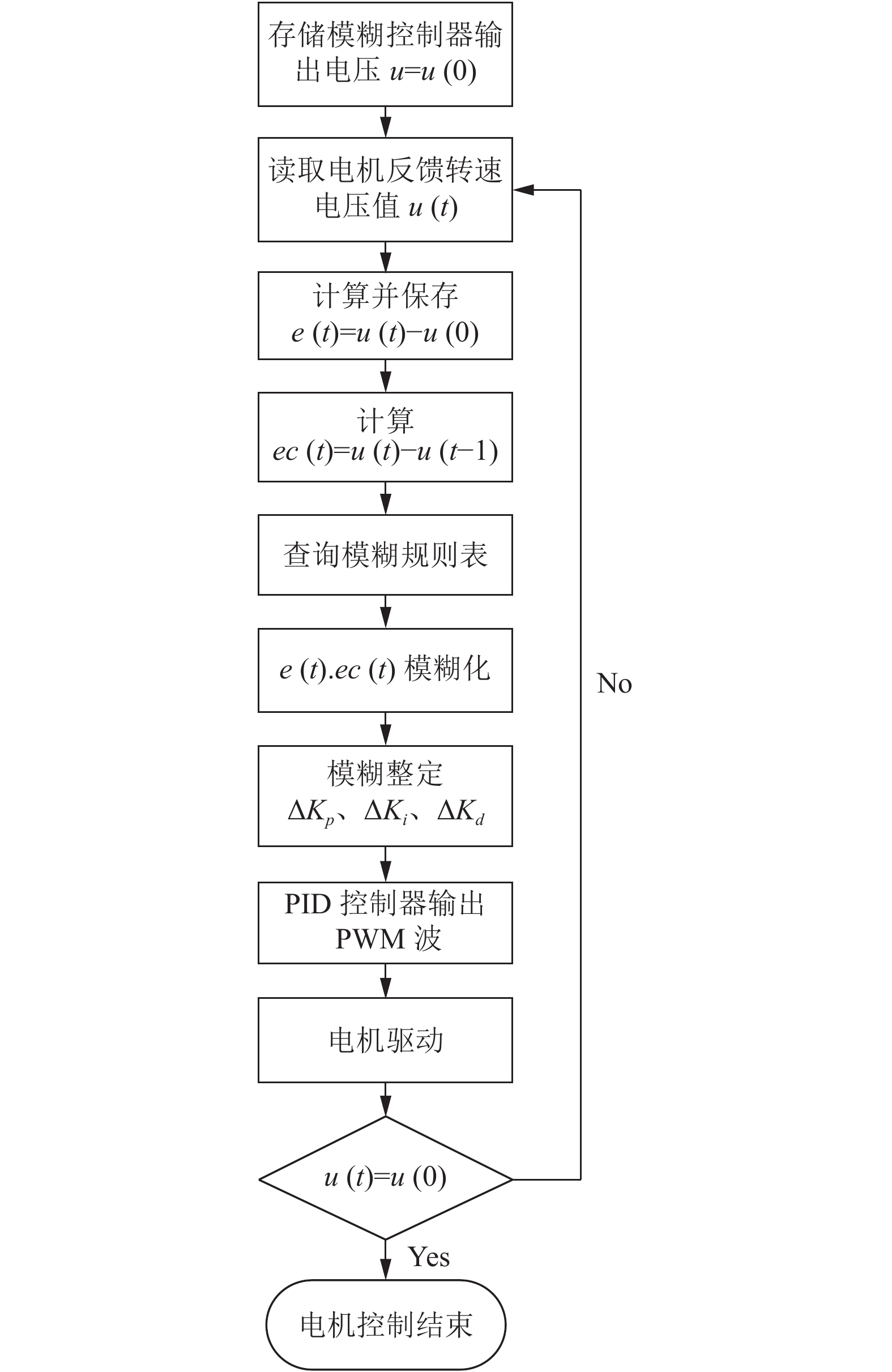
|
图 7 速控阶段算法 |
选定直流电机的参数如表4所示[16-21]. 表4中UN为额定电压, IN为额定电流, nN为额定转速, Ce为反电动势系数, Ra为电枢回路总电阻, Tl为电枢电路电磁时间常数,Tm为电力拖动系统时间常数, α为转速反馈系数根据式(6)、式(8)及表4各项参数可建立直流电机的Simulink模型如图8所示. 在该模型的基础上搭建整个光控系统的模型并进行双模糊控制算法的仿真测试.
| 表 4 直流电机参数 |

|
图 8 直流电机仿真模型 |
图9为使用Simulink中的Signal Builder模拟传感器采集到的数据. 预设光强标定值

|
图 9 传感器数据曲线 |

|
图 10 |
对比图9、图10可得,
以图10所示曲线控制电机变速, 分别使用PID控制器与模糊PID控制器F控制图8中的电机模型, 得到
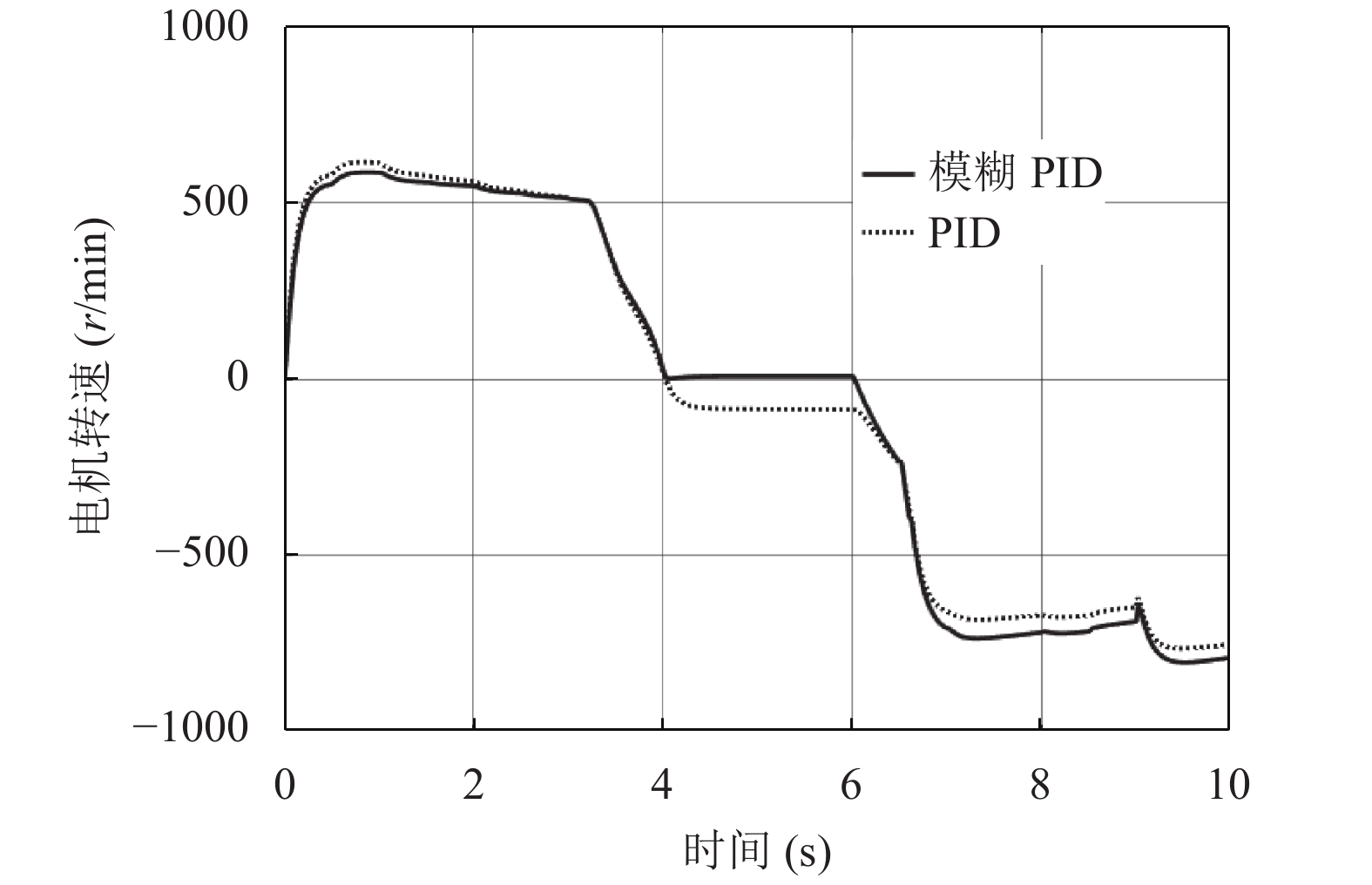
|
图 11 |
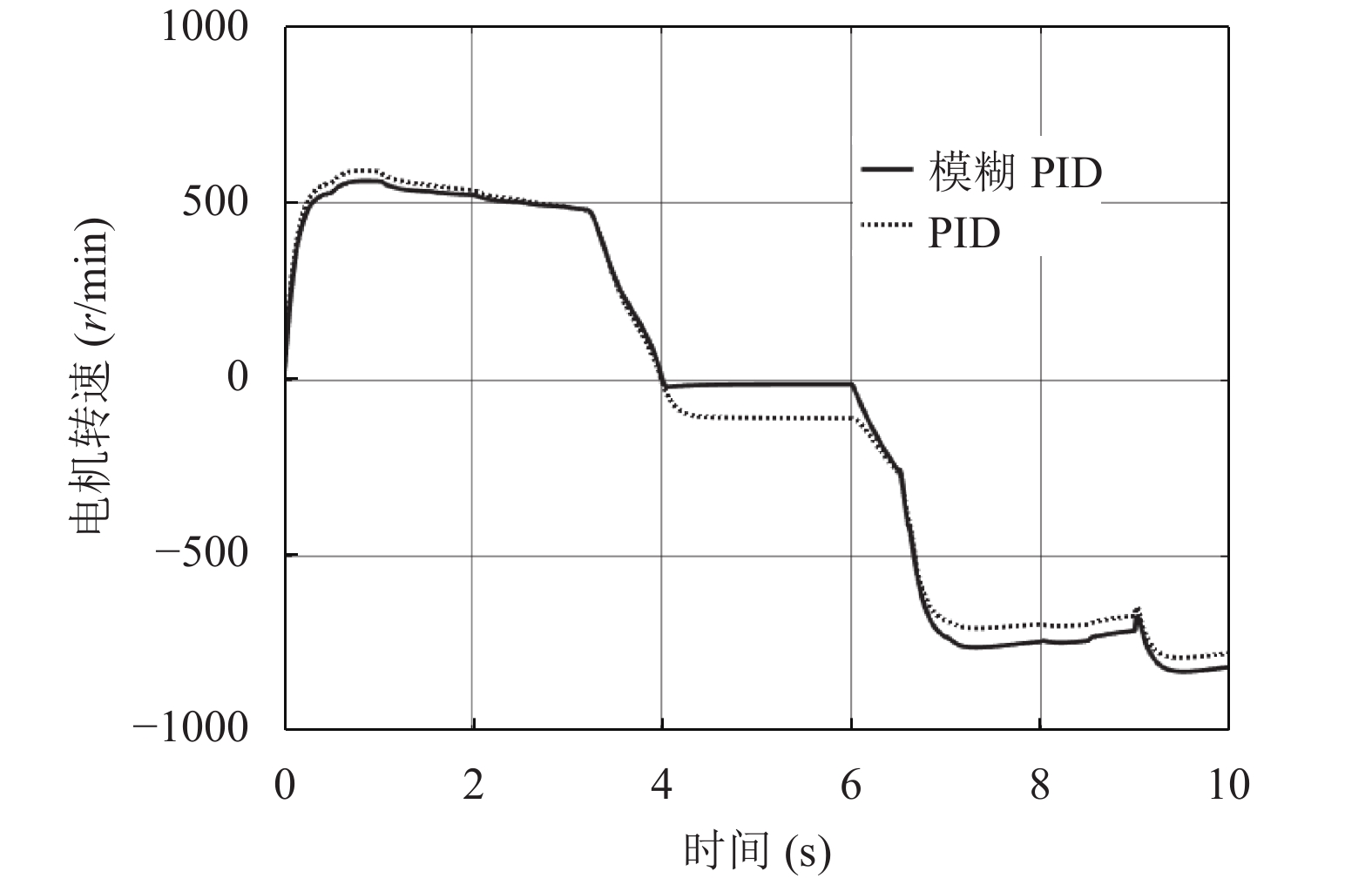
|
图 12 |
可以看到, 用普通PID的方式调节
本文设计并实现了一种应用于智能窗帘锁光控制的双模糊控制算法, 该算法能在当前光照强度及其偏差值不断变化的情况下, 实时对锁光系统的参数进行调整, 并得到准确的系统反馈值, 及时修正调整过程中的偏差, 保证了控制过程的快速与准确, 具有很好的应用前景和市场价值.
| [1] |
吴彦群. 智能窗帘悄然兴起. 致富时代, 2010(4): 57. |
| [2] |
曹显阳, 郭权龙, 杨其金, 等. 自动窗帘控制系统设计. 科技创新与应用, 2020(6): 112-113. |
| [3] |
Wong A, Tay Z, Ng J, et al. Designing smart homes for families in singapore-integrating smart home technology into daily living of elderly. Proceedings of the 17th World Congress on Ergonomics. Beijing, China. 2009. 1–2.
|
| [4] |
周敬. 基于单片机的窗帘智能控制系统设计. 天津科技, 2010, 37(2): 58-60. |
| [5] |
刘丹, 李钦晓, 费心越. 家居环境感光窗帘智能控制与调节系统. 仪器仪表用户, 2014(1): 54-58. |
| [6] |
周宁, 郑颖. 基于单片机的温控光控智能窗帘设计探讨. 南方农机, 2019, 50(4): 144. |
| [7] |
郝海燕, 董胜豪. 基于单片机的智能窗帘系统设计. 科技风, 2020(9): 10. |
| [8] |
韦发清, 杨永源, 赵芝杰, 等. 基于ESP8266WiFi模块的智能窗帘设计与实现. 电子世界, 2020(1): 135-136. |
| [9] |
刘金琨. 先进PID控制MATLAB仿真. 3版. 北京: 电子工业出版社, 2011. 288.
|
| [10] |
宋伟, 李武君. 模糊PID控制系统设计及MATLAB仿真. 云南化工, 2019(9): 156-157. |
| [11] |
刘光星, 贺刚, 张毅. 模糊PID控制在电机调速系统中的应用. 电子测试, 2019(2): 21-23. |
| [12] |
赵雨境, 孙建达. 基于模糊PID的窗帘自动控制系统设计. 闽江学院学报, 2018, 39(2): 40-47. |
| [13] |
张卫钢, 马红艳, 邱瑞, 等. 模糊PID控制算法在窗帘控制中的应用. 计算机系统应用, 2014, 23(11): 155-159. |
| [14] |
姚松, 蒋念平. 基于模糊控制理论的PID控制器的仿真研究. 计算机系统应用, 2011, 20(10): 125-128. |
| [15] |
苏兴华. 基于模糊控制理论的PID控制器设计. 中国管理信息化, 2019, 22(3): 136-139. |
| [16] |
宋绍楼, 丁永峰, 范永锋. 三相异步电机的模糊自适应PID控制系统. 计算机系统应用, 2012, 21(7): 120-123. |
| [17] |
Somwanshi D, Bundele M, Kumar G, et al. Comparison of fuzzy-PID and PID controller for speed control of DC motor using LabVIEW. Procedia Computer Science, 2019, 152: 252-260. DOI:10.1016/j.procs.2019.05.019 |
| [18] |
张琪, 雷良育, 刘国辉, 等. 基于MATLAB的直流电机特性测试. 邵阳学院学报(自然科学版), 2019, 16(3): 47-50. |
| [19] |
杨晓玫, 彭程, 吴高峰, 等. 基于Matlab的无刷直流电机控制算法建模与仿真. 系统仿真技术, 2019, 15(2): 120-125. |
| [20] |
高斌, 惠力. 直流电机转速测量与平稳性分析. 中国科技信息, 2019(6): 62-64. |
| [21] |
张国栋, 祁瑞敏. 无刷直流电机模糊PID控制系统设计与仿真. 煤矿机械, 2018, 39(1): 13-15. |
 2020, Vol. 29
2020, Vol. 29



