面向MBFL的测试用例约减策略

引用本文

杜彬, 贺杰, 王海峰, 刘勇. 面向MBFL的测试用例约减策略. 计算机系统应用, 2020, 29(12): 1-12.http://www.c-s-a.org.cn/1003-3254/7670.html

Du B, He J, Wang HF, Liu Y. Test Case Reduction Strategy for MBFL. Computer Systems and Applications, 2020, 29(12): 1-12(in Chinese).http://www.c-s-a.org.cn/1003-3254/7670.html

面向MBFL的测试用例约减策略

杜彬, 贺杰, 王海峰, 刘勇

北京化工大学信息科学与技术学院, 北京 100029

收稿日期：2020-04-07; 修改日期：2020-04-28; 采用时间：2020-05-10; csa 在线出版时间：2020-11-30

基金项目：国家自然科学基金(61902015)

通讯作者：刘勇，E-mail: lyong@mail.buct.edu.cn.

摘要：基于变异的错误定位(MBFL)是最近提出的一种自动化程序错误定位技术, 错误定位精度高, 但伴随着庞大的执行开销, 严重制约了其在工业领域的应用. 研究人员主要从减少变异体数量、减少测试用例数量和优化变异体的执行过程三个方面优化MBFL的执行效率. 前两种方法被广泛研究并取得很好的定位效果, 但对MBFL测试用例方面的研究较少, 且存在错误定位精度损失的问题. 为解决该问题, 本文提出了一种基于信息熵的测试用例约减方法(IETCR). IETCR首先计算出测试用例的信息熵, 然后根据信息熵对测试用例进行排序, 最后选择少量有价值的测试用例执行变异体. 在SIR中 6个程序100个版本上的实验结果表明, IETCR能够约减56.3%~88.6%的MBFL执行开销, 而且几乎保持与原始MBFL相同的错误定位精度.

关键词: 基于变异的错误定位信息熵测试用例约减

Test Case Reduction Strategy for MBFL

DU Bin, HE Jie, WANG Hai-Feng, LIU Yong

College of Information Science and Technology, Beijing University of Chemical Technology, Beijing 100029, China

Foundation item: National Natural Science Foundation of China (61902015)

Abstract: Mutation Based Fault Localization (MBFL) is a recently proposed approach with the advantage of high fault localization accuracy but limited to actual use in industry area since its huge mutation execution cost. Researchers improve MBFL’s execution efficiency from three aspects: reducing the number of mutants, reducing the number of test cases, and optimizing the mutant’s execution process. The former two methods were studied a lot and showed promising results, but in terms of reducing the number of test cases during MBFL, the related studies were limited for losing the precision of fault localization. In this study, we propose an Information Entropy based Test Cases Reduction strategy (IETCR) for MBFL. IETCR first calculates the information entropy of test cases, then sorts them according to the information entropy. Finally, it selects a small number of valuable test cases to execute mutants. Empirical studies are conducted on 100 fault versions of 6 programs from the SIR repository. The results show that IETCR can reduce 56.3%–88.6% mutation execution cost while keeping almost the same fault localization accuracy with the original MBFL.

Key words: Mutantion Based Fault Localization (MBFL) information entropy test case reduction

1 引言

软件已经成为现代生活中的重要组成部分, 并在医学、航天学和原子能等方面发挥着重要的作用. 在软件的开发和维护中, 软件调试是一项成本昂贵且复杂耗时的工作^[1]. 软件调试包括软件检测、错误定位和错误修复^[2]. 其中, 错误定位旨在自动识别软件缺陷模块, 是提高软件调试效率的最有效手段之一.

近年来, 研究人员在软件自动化错误定位领域上花费巨大的精力, 用于降低软件调试过程中人力财力的消耗^[1,3]. 其中, 基于频谱的错误定位方法是一种被广泛应用的错误定位方法^[4,5]. 基于频谱的错误定位方法通过执行测试用例获得覆盖信息和执行结果信息来计算程序实体中含有错误的概率, 然后依据概率大小生成怀疑度表来定位错误. 但该方法未考虑程序控制流对程序的影响, 并且未能处理偶然正确测试用例, 使得错误定位的有效性受到影响. 此外, 基于频谱的错误定位方法依赖于测试用例在程序实体上的覆盖信息, 所有同一基本块的语句会共享相同的覆盖信息, 计算得到的排名也会相同, 因此需要检查更多的程序实体才能检测到错误^[6], 导致其定位精度降低. 为了解决上述问题, 研究人员提出了基于变异的错误定位方法来协助错误定位. 基于变异的错误定位方法是一种基于变异分析的方法^[7], 拥有较高的错误定位精度. 依据对变异体的分析角度, 基于变异的错误定位方法分为两种, Metallax-fl^[8]和MUSE^[9]. Metallax-fl采用变异分析的思想, 将变异体视为被测程序的相似版本^[8]; MUSE结合了变异分析, 将变异体视为被测程序的部分修复^[9]. Pearson等的研究表明, Metallax-fl在错误定位精度和效率方面都优于MUSE^[10].

基于变异的错误定位方法虽然有较高的错误定位精度, 但伴随巨大的执行开销 ^[11]. 因此研究人员着力于降低其执行开销, 主要从3个方面进行: (1)减少变异体的数量; (2)减少测试用例的数量; (3)优化执行过程. Mathur等提出的SELECTIVE策略通过选择部分变异算子来替代原始的变异算子集合, 从而减少生成的变异体数量 ^[12]. 另一方面, SAMPLING方法通过从变异体集合中抽取部分变异体来减少变异体的数量^[11]. 从测试用例角度, de Oliveira等提出了FTMES, 该方法只采用失败测试用例执行变异体, 用通过测试用例的覆盖信息作为变异杀死信息来减少测试用例的执行开销^[13]. 优化执行过程方面, Liu等提出的DMES策略通过动态优化变异体和测试用例的执行来提升MBFL的效率^[14].

由于MBFL执行开销约减策略中, 约减测试用例角度的研究工作很少, 并受Yoo等的工作启发^[15], 测试用例在程序测试过程中含有不同的信息或作用, 本文提出一种基于信息熵的测试用例约减策略, IETCR, 利用信息熵理论对通过测试用例进行排名, 最终选择部分检错能力强的通过测试用例和所有失败测试用例, 从而减小MBFL的执行开销. 进一步的实验证明该策略能有效降低MBFL开销, 而且没有明显降低错误定位精度.

2 相关背景 2.1 基于变异的错误定位技术

基于变异的错误定位技术是一种基于变异分析的错误定位方法. 变异分析的概念由Demillo等首先提出, 通过对被测程序的源代码进行微小的改变^[16], 然后生成错误程序, 也就是变异体^[17]. 生成变异体的规则被称为变异算子^[18]. 在变异分析的过程中, 如果一个变异体的执行结果不同于原始程序的结果, 那么这个变异体被杀死, 记为killed或distinguished, 反之则为not killed或alive.

基于变异的错误定位技术的提出, 建立在变异体的行为和部分含真实错误的被测程序的表现极为相似这一基础上^[1], 变异体与测试用例集错误检测有很强的联系. 基于变异的错误定位技术主要包含以下4个步骤:

(1)获得被失败测试用例覆盖的语句: 将测试用例T执行被测程序P, 获得覆盖信息和执行结果(pass或fail). 然后将测试用例划分为通过测试用例集合T_p和失败测试用例集合T_f. 结合覆盖信息可获得被失败测试用例覆盖的语句集合, 用Cov_f表示^[19].

(2)生成和执行变异体: 采用不同变异算子, 对失败测试用例覆盖的语句植入错误生成变异体. 对某一条语句s, 使用不同变异算子会生成不同的变异体, 变异体集合记为M(s). 然后测试用例执行所有的变异体, 依据执行结果, T_k为杀死变异体的测试用例集合, T_n为未杀死变异体的测试用例集合.

表 1 常用怀疑度计算公式

(4)生成错误定位报告: 依据程序语句怀疑度的大小, 降序排列生成程序语句排名表. 开发人员可以根据排名表从上至下查找并修正程序错误.

2.2 MBFL的开销约减策略

基于变异的错误定位技术在已有的研究工作中表现出较高的错误定位精度, 但伴随着巨大的时间开销, 为了提升该技术的效率, 研究人员从3个方面提出了优化策略:

(1)减少变异体的数量: 这项策略旨在减少变异体数量, 因为更少的变异体被执行, 那么变异执行开销相应也就减小. 从减少变异算子的角度, Papadakis等提出一种变异算子约减策略SELECTIVE, 该策略针对变异算子定义了特别的“充分准则”^[16]. 依照准则, 一些更“充分”的变异算子会被保留下来用于生成变异体, 其余贡献值更小的则被忽略, 从而减少变异体的数量. 从直接减少变异体的角度, SAMPLING策略随机从全体变异体集合中抽取固定比例的变异体用于执行测试用例^[8]. Liu等提出的SOME策略从语句层面对变异体进行抽样^[25].

(2)减少测试用例的数量: 该策略通过减少测试用例在变异体上的执行数量来减少执行开销. de Oliveira等提出了FTMES, 用通过测试用例的覆盖信息代替其变异体杀死信息, 对变异体只执行失败测试用例, 进而约减了变异体执行通过测试用例的开销^[13]. 由于通过测试用例对错误定位仍然具有一定的价值, FTMES策略会造成定位精度的损失.

(3)优化执行过程: 该策略通过优化变异体和测试用例的执行过程来减少开销. Liu等提出一项动态变异体执行优化策略DMES, 其包括两种优化方案, 变异体执行优化MEO和测试用例执行优化TEO^[14]. DMES使用了变异体全集和测试用例全集, 因此可以结合其他策略, 进一步约减MBFL的执行开销.

本文提出的IETCR策略, 是一种减少测试用例执行的策略. 该策略与FTMES的研究角度相同, 但FTMES对变异体只执行了失败测试用例, 忽略了通过测试用例, 而IETCR策略同时保留了通过和失败测试用例, 进而减少了错误定位精度的损失.

3 基于信息熵的测试用例约减策略

测试用例集中每个测试用例的检错能力不同, 且测试用例间存在冗余, 检错能力强的测试用例能提高被测程序中错误语句, 降低非错误语句在怀疑度表中的排名; 反之, 检错能力弱的测试用例则降低错误语句, 提高非错误语句在怀疑度表中的排名. 因此, 为了减少MBFL执行的测试用例个数, 提高运行效率, 应该选择检错能力强的测试用例, 去除检错能力弱的测试用例. 本文使用信息熵作为测试用例检错能力的衡量指标, 并据此提出了一种基于信息熵的测试用例约减方法IETCR (Information Entropy based Test Case Reduction). 该方法选择全部失败的测试用例和少量有价值的通过测试用例进行错误定位, 减少了测试用例的数量, 同时保证了测试用例集的质量, 不会造成明显的错误定位精度损失.

3.1 测试用例的信息熵

信息熵是指信息中排除了冗余后的平均信息量, 由信息论之父Shannon提出^[26]. 任何信息都存在冗余, 冗余大小与信息中每个符号的出现概率(不确定性)有关, 出现的概率大, 不确定性小; 反之不确定性大. 令不确定函数为F, 概率为P, 从上述信息熵的定义可知, 不确定函数F是概率P的减函数, 两个独立符号所产生的不确定性应该等于各自的不确定性之和, 如式(1)所示:

$F({p_1},{p_2}) = F({p_1}) + F({p_2}),{\rm{ }}F(p) = - {\log _2}p$

(1)

若信源符号有n种取值, $U{\rm{ = }}\{ {u_1},{u_2}, \cdots ,{u_n}\} $ , 对应的概率 $P = \{ {p_1},{p_2}, \cdots ,{p_n}\} $ , 则信源的信息熵如式(2)所示:

$H(U) = - \sum\nolimits_{i = 1}^n {{p_i}} \times {\log _2}{p_i}$

(2)

错误定位是一个依据测试用例提供的执行结果信息, 消除软件中错误语句不确定性的过程, 该过程中的信息量可以用信息熵表示. 依据上述信息熵的基本概念, 在错误定位的过程中, 被测程序 $program = \{ {s_1},{s_2}, \cdots ,{s_m}\} $ 由m条语句组成, 假设其中只有一条语句包含错误, 且每条语句是否为错误语句不确定, 则被测程序即可作为信源, 程序中每条语句对应信息中的每个符号, 语句是错误语句的概率为信息中对应符号出现的概率, 因此, 错误定位过程中的信息量可用信息熵衡量, 信息熵越小, 表明软件中错误语句的不确定性越小; 反之不确定性越大.

测试用例的检错能力可以用引入该测试用例后, 错误定位过程中信息熵的下降程度衡量. 错误定位的过程中, 依据测试用例执行结果提供的信息来确定错误语句出现的位置, 消除软件中错误语句的不确定性, 因此, 一个测试用例的性能就可以用引入该测试用例后, 错误定位过程信息熵的下降程度来衡量. 执行测试用例后, 错误定位过程信息熵下降的程度大, 表明该测试用例能很好地区分被测程序中的错误语句和其他语句; 反之则说明这一测试用例不能有效区分被测程序中的语句, 执行该测试用例对错误定位的结果贡献不大. 基于这一思路, 可以按照检错能力对测试用例进行排序, 在错误定位的过程中只选择排名靠前, 性能优异的测试用例执行, 从而减少执行的测试用例数量, 降低错误定位过程中的执行开销.

使用归一化后的语句怀疑度值估计语句为错误语句的概率, 进而计算测试用例的信息熵. SBFL方法执行开销小, 只需测试用例的执行结果和覆盖信息即可计算被测程序语句的怀疑度值, 因此, 可以使用归一化后的语句怀疑度值表示该语句是否为错误语句的概率. 具体而言, 给定包含m条语句的被测程序 $program = \{ {s_1},{s_2}, \cdots ,{s_m}\} $ 和包含n个测试用例的测试用例集 $T = \{ {t_1},{t_2}, \cdots ,{t_n}\} $ , 移除测试用例 ${t_i}$ 后的测试用例集用 ${T_{remove - i}} = \{ {t_1}, \cdots ,{t_{i - 1}},{t_{i + 1}}, \cdots ,{t_n}\} $ 表示, $Sus(s|{T_{remove - i}})$ 表示使用测试用例集 ${T_{remove - i}}$ 计算得到的语句 ${s_i}$ 的怀疑度值, $P({s_i}|{T_{remove - i}})$ 表示该语句为错误语句的概率, 如式(3)所示:

$P({s_i}|{T_{remove - i}}) = \frac{{Sus({s_j}|{T_{remove - i}})}}{{\displaystyle\sum\nolimits_{j = 1}^m {Sus({s_j}|{T_{remove - i}})} }}$

(3)

计算出每个语句为错误语句的概率, 就可计算出错误定位过程中整个测试用例集的信息熵, 如式(4)所示:

$H({T_{remove - i}}) = - \sum\nolimits_{j = 1}^m {{P_{({s_j}|{T_{remove - i}})}}} \times {\log _2}{P_{({s_j}|{T_{remove - i}})}}$

(4)

移除指定测试用例前后, 信息熵的差值即为该测试用例的信息熵, 计算过程如式(5)所示. $H({t_i})$ 越小, 说明执行测试用例 ${t_i}$ 后, 错误定位过程的信息熵越低, 错误语句的不确定性越小, 错误定位结果越好, 该测试用例应该被保留; 反之该测试用例应该被移除.

$H({t_i}) = H(T) - H({T_{remove - i}})$

(5)

依据信息熵理论, 可以将测试用例集中每个测试用例的检错能力进行量化, 为测试用例的约减提供重要信息. 将测试用例按照信息熵从小到大排序, 得到测试用例执行序列, 排在序列前端的测试用例能更加有效地区分被测程序中的错误语句和其他语句, 因此被优先执行.

3.2 IETCR方法框架

IETCR使用信息熵衡量测试用例的检错能力, 选择全部失败的测试用例和少量有价值的通过测试用例进行错误定位, 减少了执行的测试用例数量, 同时保证整个测试用例集的质量, 具体执行框架如图1所示.

图 1 IETCR方法框架

图1中, IETCR分为4个阶段, 第一阶段为测试用例执行阶段, 被测程序执行测试用例集, 测试用例的语句覆盖信息和执行结果信息被收集; 第二阶段为测试用例约减阶段, 依据第一阶段获得的测试用例执行结果信息, 将测试用例集分成通过的测试用例(passed test cases)和失败的测试用例(failed test cases)两部分. 对于执行通过的测试用例, 计算每个测试用例的信息熵, 并按信息熵从小到大排列成一个执行序列; 对于执行失败的测试用例, 则全部加入到下一阶段的测试用例执行序列中. 从排好序的通过测试用例序列中选择与失败测试用例个数相同的通过测试用例加入下一阶段的测试用例执行序列中, 作为第三阶段变异体执行的测试用例集; 第三阶段为变异体生成和执行阶段, 依据变异算子定义的规则, 对被失败测试用例所覆盖的语句植入故障, 生成大量的变异体, 每一个变异体都要执行第二阶段选择出来的测试用例集, 并记录变异体在测试用例上的执行结果信息; 第四阶段为怀疑度表生成阶段, 首先依据第三阶段得到的变异体执行信息, 选择合适的怀疑度公式, 计算每个变异体的怀疑度值, 然后再依据变异体的怀疑度值计算可疑语句的怀疑度值, 最后将可疑语句按怀疑度值从大到小排序, 即可得到故障程序的怀疑度表. 开发者按照怀疑度表中的顺序依次检查源代码, 直到准确定位程序中的故障.

IETCR方法的有效性取决于每个通过测试用例的信息熵, 信息熵计算的越准确, 使用IETCR方法所取得的效果越好. 最新提出的SBFL怀疑度公式是Dstar, 试验结果表明, Dstar公式在定位单错误和多错误时都具有高于其他怀疑度公式的错误定位精度^[23]. 因此, 本文使用Dstar公式计算测试用例的信息熵. 具体算法如算法1所示.

算法1. 基于信息熵的测试用例约减

输入: 被测程序P, 测试用例集T

输出: 约减后的测试用例集合reducedTestCaseSet

1. Cov, R ← execute(P, T);

2. for all s in P do

3.　 Sus(s);

4. failed, passed ← split(T, R);

5. failedNum ←size(failed);

6. entropySet ← $\scriptstyle\emptyset$ ;

7.H(T) ← getEntropy(T);

8.　 for test case t in passed do

9.　 H( $\scriptstyle{T_{remove - i}}$ ) ← getEntropy( $\scriptstyle{T_{remove - i}}$ );

10.　 entropySet ← H(T) - H( $\scriptstyle{T_{remove - i}}$ );

11. end for

12. reducedTestCaseSet ← failed;

13. sorted(entropySet);

14. reducedTestCaseSet ← select(entropySet, failedNum);

15. return reducedTestCaseSet;

算法1描述了使用IETCR方法进行测试用例约减的伪代码, 算法的输入是被测程序P和对应的测试用例集T, 输出为约减后的测试用例集合reducedTestCaseSet. IETCR首先获取测试用例的语句覆盖信息Cov和测试用例的执行结果R, 并使用这些执行信息计算出被测程序中语句的怀疑度值(1~3行), 接着依据测试用例的执行结果, 将测试用例分为失败的测试用例和通过的测试用例, 并且记录失败测试用例的数量, 初始化EntropySet, 以便之后测试用例的选择(4~6行), 计算出T的信息熵(7行), 最后对 ${T_p}$ 中的每一个测试用例, 计算其信息熵并加入到EntropySet(8~11行), 至此, 测试用例信息熵的计算完成, 接下来依据信息熵选择要执行的测试用例. 先将failed加入到reducedTestCaseSet (12行), 然后对EntropySet中通过的测试用例按信息熵从小到大排序(13行), 依次将前failedNum个测试用例加入到reducedTestCaseSet并返回(14~15行), 到此整个算法结束.

3.3 IETCR方法示例

结合具体示例, 对算法1中的关键步骤(8~14行)进行详细介绍. 在表2中, 从左往右, 第一列为被测程序的源码, 接下来的6列分别为6个测试用例及其覆盖被测程序的信息, 其中“1”表示覆盖, “0”表示不覆盖, 最后一列为使用怀疑度公式Dstar计算出的语句怀疑度值. 倒数第二行为测试用例的执行结果信息, 倒数第一行是使用公式Dstar计算得到的通过测试用例的信息熵. 在上表中, 按信息熵从小到大排序后的测试用例执行序列为 ${T_p} = \{ {t_1},{t_6},{t_3},{t_4}\} $ , 选择与失败测试用例相同数量的通过测试用例执行, 因此, 约减后的测试用例序列为 ${T_R} = \{ {t_1},{t_2},{t_5},{t_6}\} $ .

表 2 被测程序及其测试用例覆盖信息

Program	t₁(3,3,5)	t₂(1,2,3)	t₃(3,2,1)	t₄(5,5,5)	t₅(5,3,4)	t₆(2,1,4)	Sus
1 int m;	1	1	1	1	1	1	2.00
2 m = z;	1	1	1	1	1	1	2.00
3 if(y<z–1)//fault	1	1	1	1	1	1	2.00
4 if(x<y)	1	0	0	0	0	1	0.00
5 m = y;	0	0	0	0	0	0	0.00
6 else if(x < z)	1	0	0	0	0	1	0.00
7 m = x;	1	0	0	0	0	1	0.00
8 else	0	1	1	1	1	0	4.00
9 if(x>y)	0	1	1	1	1	0	4.00
10 m = y;	0	0	1	0	1	0	0.50
11 else if(x>z)	0	1	0	1	0	0	0.50
12 m =x;	0	0	0	0	0	0	0.00
13 return m;}	1	1	1	1	1	1	2.00
执行结果	P	F	P	P	F	P	—
信息熵	2.7e–11	—	3.9e–10	3.9e–10	—	2.7e–11	—

表 2 被测程序及其测试用例覆盖信息

表3描述了示例被测程序生成的变异体及在测试用例上的执行信息. 从左到右, 第1列为被测程序的源代码, 第2列为对应语句生成的变异体集合, 第3列划分为6部分, 分别是6个测试用例在变异体上的执行信息, 其中“1”表示测试用例杀死对应的变异体, “0”表示测试用例没有杀死对应的变异体, 最后一列分为两部分, “original”表示使用原始MBFL方法, 变异体对应的怀疑度值, ‘IETCR’表示使用IETCR方法, 变异体对应的怀疑度值, 加粗部分为对应语句生成的变异体中怀疑度值的最大值.

表 3 被测程序变异体及其执行结果信息

Program(P)	Mutants	Test suite						Suspiciousness
Program(P)	Mutants	${t_1}$	${t_2}$	${t_3}$	${t_4}$	${t_5}$	${t_6}$		Original	IETCR
1 int m;
2 m = z;
3if(y<z–1) //fault	M1: <→ ≤	0	1	0	0	1	0	+∞		+∞
	M2: < → >	1	0	1	0	0	1	0.00		0.00
	M3: < → ≥	1	1	1	0	1	0	4.00		8.00
	M4: < → ==	1	1	0	0	1	1	4.00		0.00
	M5: < →!=	0	0	1	0	0	0	0.00		0.00
	M6: < → true	0	1	1	0	1	0	8.00		0.00
	M7: < → false	1	0	0	0	0	1	0.00		0.00
4 if(x<y)	M8: <→ ≤	0	0	0	0	0	0	0.00		0.00
	M9: < → >	0	0	0	0	0	1	0.00		0.00
	M10: < → ≥	0	0	0	0	0	0	0.00		0.00
	M11: < → ==	0	0	0	0	0	0	0.00		0.00
	M12: < →!=	0	0	0	0	0	1	0.00		0.00
	M13: < → true	0	0	0	0	0	1	0.00		0.00
	M14:< → false	0	0	0	0	0	0	0.00		0.00
5 m = y
6 else if(x<z)	M15: <→ ≤	0	0	0	0	0	0	0.00		0.00
	M16: < → >	1	0	0	0	0	1	0.00		0.00
	M17: < → ≥	1	0	0	0	0	1	0.00		0.00
	M18: < → ==	1	0	0	0	0	1	0.00		0.00
	M19: < →!=	0	0	0	0	0	0	0.00		0.00
	M20: < → true	0	0	0	0	0	0	0.00		0.00
	M21:< → false	1	0	0	0	0	1	0.00		0.00
7 m = x;
8 else
9 if(x>y)	M22: >→ ≤	0	1	0	0	0	0	1.00		1.00
	M23: > →<	0	0	1	0	1	0	0.50		1.00
	M24: > → ≥	0	1	1	0	1	0	8.00		0.00
	M25: > → ==	0	0	1	0	1	0	0.50		1.00
	M26: > →!=	0	1	1	0	1	0	8.00		0.00
	M27: > → true	0	1	0	0	0	0	1.00		1.00
	M28:> → false	0	0	0	0	0	0	0.00		0.00
10 m = y
11 else if(x>z)	M29: >→ ≤	0	0	0	0	0	0	0.00		0.00
	M30: > →<	0	1	0	0	0	0	1.00		1.00
	M31: > → ≥	0	1	0	0	0	0	1.00		1.00
	M32: > → ==	0	0	0	0	0	0	0.00		0.00
	M33: > →!=	0	1	0	0	0	0	1.00		1.00
	M34: > → true	0	1	0	0	0	0	1.00		1.00
	M35:> → false	0	0	0	0	0	0	0.00		0.00
12 m = x;

表 3 被测程序变异体及其执行结果信息

在上述示例中, IETCR方法只执行了4个测试用例, 降低了33.3%的执行开销, 同时没有任何精度损失. 具体而言, 首先使用SBFL技术和怀疑度公式Dstar计算被测程序中语句的怀疑度值, 然后依据式(5)计算出每个通过测试用例的信息熵, 以测试用例 ${t_1}$ 为例, 当执行全部的测试用例时 $H(T)$ = 3.700439717995333, 将 ${t_1}$ 从测试用例集中移除, 此时测试用例的信息熵 $H({T_{remove - 1}})$ =3.7004397179680146, 因此, ${t_1}$ 消除的信息熵 $H({t_1})$ =2.73e–11. 同理, ${t_3}$ , ${t_4}$ , ${t_6}$ 消除的信息熵分别为3.91e–10, 3.91e–10, 2.73e–11. 根据上述测试用例的信息熵, IETCR方法选择其中信息熵最低的两个测试用例 ${t_1}$ 和 ${t_6}$ 加入执行序列, 对于 ${t_3}$ 和 ${t_4}$ 将不在执行. 执行测试用例 ${t_1}$ , ${t_2}$ , ${t_5}$ , ${t_6}$ , 使用测试用例在变异体上的执行信息计算对应变异体的怀疑度值, 如表3 IETCR列所示. 与原始MBFL相比, 使用IETCR方法计算出的语句怀疑度值没有发生变化, 错误语句3排在怀疑度表的首位, 被优先检查. 在上述示例中, 与原始MBFL相比, IETCR少执行了 $2 \times 35 = 70$ 次MTP, 降低了33.3%的执行开销, 而且没有任何精度损失.

4 实验评估 4.1 研究问题

为了评估IETCR方法的有效性, 本文从错误定位精度和约减率两方面出发, 提出如下研究问题.

RQ1: 与原始MBFL方法以及其他测试用例约减方法FTMES, SAMP 30%相比, IETCR方法的约减率如何?

RQ2: 与原始MBFL方法以及其他测试用例约减方法FTMES, SAMP 30%相比, IETCR方法的错误定位精度如何?

RQ3: IETCR方法的影响因素和额外执行开销有哪些?

4.2 实验对象与环境配置

针对以上研究问题, 本文选择了错误定位领域常用的软件基准程序库(Software-artifact Infrastructure Repository, SIR)^[27]中的6个程序作为实验对象, 分别为printtokens, schedule, totinfo, tcas, sed, grep. 这些程序均为开源的C程序. 以上程序共包含了117个错误版本, 部分版本错误语句无法植入故障生成有效变异体, 因此测试用例无法检测出该版本中的错误, 或者执行过程中出现异常, 无法搜集到完整的执行信息. 在本文中, 选择了其中100个错误版本程序作为实验对象. 表4列出了具体信息. 在进行实验时, 使用Gcov^[28]搜集测试用例的语句覆盖信息, 利用软件测试领域中广泛使用的变异测试工具Proteum/IM2.0^[29]来对被测程序语句进行变异, 获取变异体相关信息. 所有的实验都运行在Linux (系统版本 3.10.0-957.c17.x86-64, CPU Intel(R) Gold 6240 @2.60 GHz 18 cores)系统下.

表 4 实验基准程序相关信息

4.3 评估指标

对于错误定位精度, 本文使用EXAM Score^[16]和TOP-N%^[30,31]衡量, 同时使用秩和检验分析测试用例约减方法与原始MBFL之间是否存在显著性差异. EXAM Score是错误定位领域广泛使用的评价指标之一, 使用发现错误语句时, 检查的语句数量占需要检查的语句总数量的百分比来表示, 因此, EXAM Score值越小, 表明错误定位精度越高, 具体如式(6)所示. 式(6)中Rank表示错误语句的排名, Number表示被检查语句的数量. 在实际的错误定位中, 很多语句具有相同的怀疑度值, 这就导致了它们在怀疑度表中具有相同的排名, 在最理想的情况下, 实际错误语句被第一个检查, 在最糟糕的情况下, 实际错误语句被最后一个检查. 对于怀疑度相同的语句, 本文使用它们的平均排名来计算错误定位精度.

$EXAM\;Score = \frac{{Rank}}{{Number}}$

(6)

TOP-N%表示检查N%的代码时, 能定位被测程序中错误的百分比, 用来衡量错误定位方法能否准确定位被测程序中的部分错误. 在错误定位过程中, 能精确定位小部分错误比模糊定位大部分错误更有实用意义. 秩和检验是一种非参数检验, 不依赖于总体分布的具体形式, 本文用来分析两种错误定位方法的错误定位精度之间是否存在显著性差异^[32].

本文使用MTP (Mutant-Test-Pair)执行次数衡量方法的执行开销, 通过约减率评估对应方法降低MBFL执行开销的程度. 使用MTP次数作为错误定位方法执行开销的衡量指标, 评估的准确度不受具体实现与使用环境的影响^[33]. 约减率是指对应方法减少的MTP次数所占的百分比, 约减率越大, 方法降低MBFL执行开销的程度越大.

对于RQ1, RQ2, RQ3中的问题, 实验使用表1中的5个怀疑度公式, 通过原始MBFL, SAMP 30%, FTMES等方法, 对表4中6个程序共100个版本进行错误定位, 统计每个版本的EXAM Score, 方法运行时间和执行的MTP次数. 为了保证对比效果, 对于SAMP 30%方法, 同时重复试验50次, 消除随机抽样对本组试验的影响.

4.4 实验结果 4.4.1 约减效率

为了探究RQ1, 本文选择了测试用例约减方法SAMP 30%, FTMES和原始MBFL作为对照组, 使用表1中的5个怀疑度公式, 分别统计它们在上述6个程序100个版本中定位错误所执行的MTP次数, 试验结果示例如图2, 是上述6个程序中的printtokens, 在柱状图中, X轴代表对应程序中的版本号, Y轴代表执行的MTP次数, 每一列包含4部分, 从下往上依次是IETCR, FTMES, SAMP 30%和原始MBFL, 分别用黑色, 深灰, 浅灰和白色表示. 所有程序结果如图3所示.

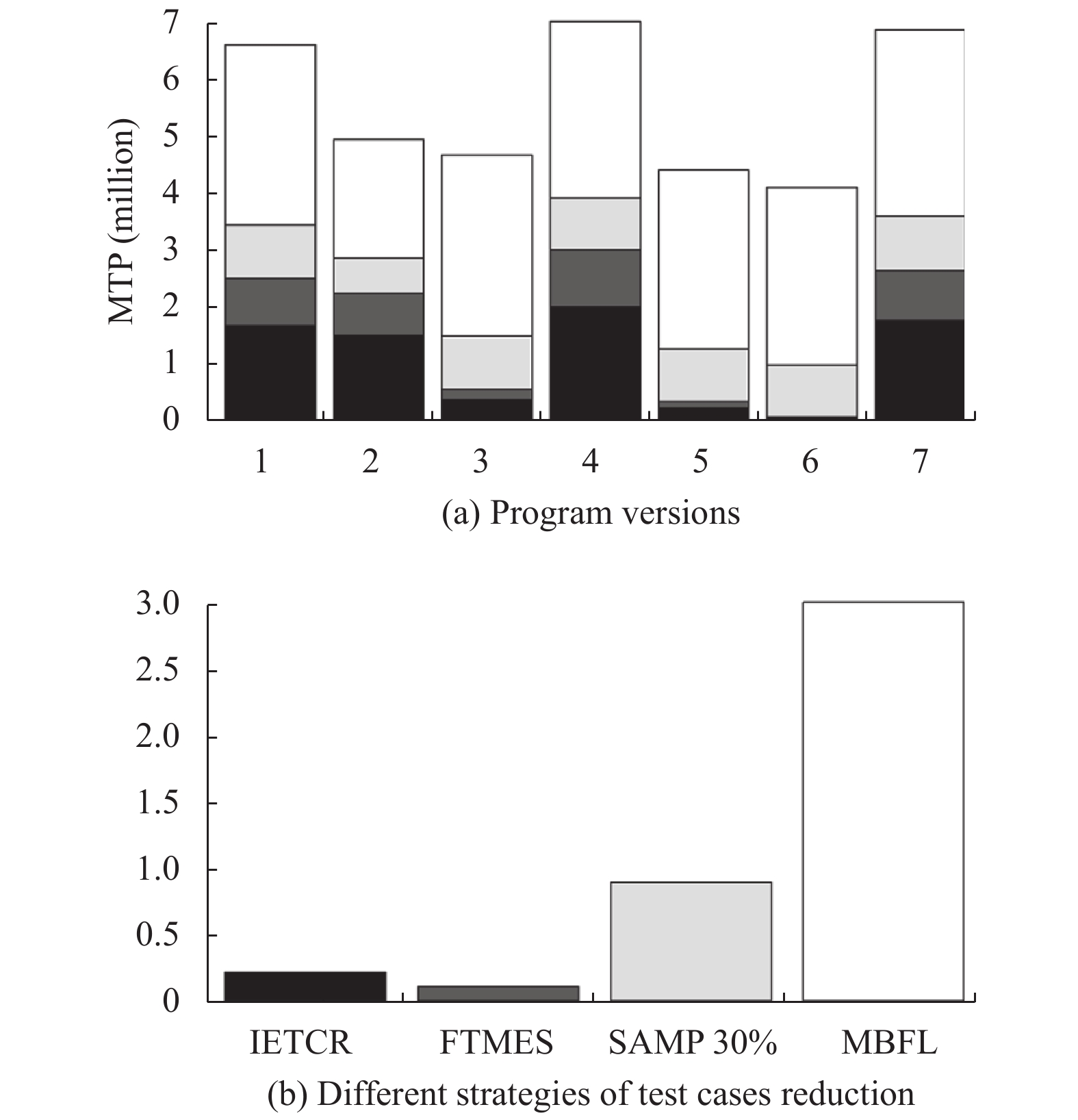
图 2 MBFL约减方法的执行开销示例 (printtokens)

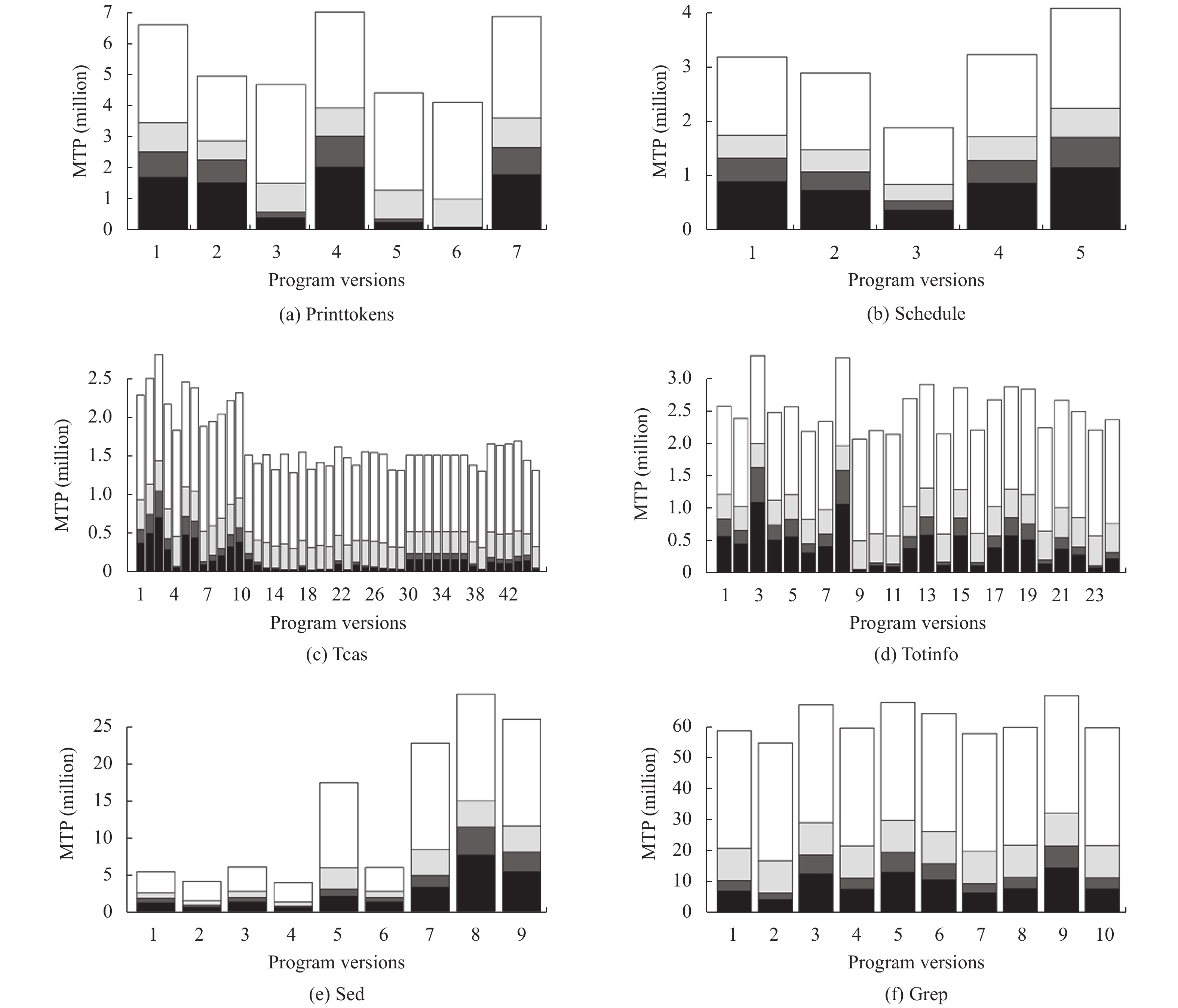
图 3 MBFL约减方法的执行开销

图3中, 大多数情况下, 黑色部分明显小于白色部分, 特别是在被测程序tcas中, 表明与原始MBFL相比, IETCR方法可以显著降低执行开销. 图中深灰部分所占的比例最小, 说明在以上3种方法中, FTMES定位错误执行的MTP次数最少.

为了更准确地进行比较, 表5列出了IETCR, FTMES, SAMP 30%在实验程序中的平均约减率.

表 5 IETCR, FTMES, SAMP 30%方法的约减率(%)

如表5所示, IETCR方法的约减率(71.0%)介于FTMES(82.8%)和SAMP 30%(70.0%)方法之间, FTMES方法的约减率最高. 其原因是, FTMES只执行了失败的测试用例, 而本文提出的方法IETCR不仅执行了失败的测试用例, 还执行了同等数量的通过测试用例. 由于同时执行了少量有价值的通过测试用例, IETCR方法的错误定位精度优于FTMES方法, 具体比较见4.4.2节.

4.4.2 方法的错误定位精度

为了探究RQ2, 本文选择了原始MBFL, 测试用例约减方法FTMES, SAMP 30%作为对照组, 同时使用表1中的5个怀疑度公式, 统计它们在上述实验程序中的EXAM Score, 试验结果如图4所示. 图4共包含5部分, 对应5个不同的MBFL怀疑度公式. 在每个子图中, X轴表示不同的测试用例约减方法, Y轴表示对应方法的EXAM Score, 子图中每一个类似小提琴的部分都表示一种测试用例约减方法在上述实验程序上的错误定位精度分布, 其中, 外部形状为核密度估计, 内部白色的点是中位数, 黑色盒型的范围是下四分位点到上四分位点. 对应方法的错误定位精度分布在Y轴较低位置的宽度越宽, 较高位置的宽度越窄, 表示对应的方法定位错误需要检查的语句越少, 错误定位精度越高.

在图4的全部5个怀疑度公式中, 本文提出的方法IETCR几乎与原始MBFL具有相同的数据分布, 与其他方法相比, IETCR方法EXAM Score的分布更接近原始MBFL. 因此, 与原始MBFL相比, IETCR没有明显降低错误定位精度, 并且明显优于其他测试用例约减方法SAMP 30%和FTMES. 对于SAMP 30%, FTMES方法而言, 错误定位效果较好的是SAMP 30%, FTMES次之.

为了更加精确地比较IETCR方法的定位效果, 表6分别列出了原始MBFL, IETCR, SAMP(30%)方法的EXAM Score值在不同检查比例下所占的百分比, 即TOP-N%值. 从表6中的数据可观察到, 使用IETCR方法的错误定位精度几乎等同于原始MBFL技术, 优于现有方法FTMES和SAMP 30%. 具体而言, 以第3行前两列<1%, 0.31>为例, 表示使用怀疑度公式Jaccard(JA)对所有版本检查1%的代码时, 原始MBFL方法可以定位其中31%的错误, 加粗部分表示使用对应怀疑度公式和检查比例, 原始MBFL, IETCR, SAMP 30%方法定位错误百分比的最大值. 使用全部怀疑度公式, 对所有版本检查1%的代码, IETCR方法定位到的错误所占比例为: 0.29(JA), 0.29(OC), 0.27(OP), 0.02(TA), 0.28(DS), 原始MBFL能够定位到的错误比例为: 0.31(JA), 0.31(OC), 0.27(OP), 0.05(TA), 0.30(DS), 与原始MBFL方法相比, IETCR定位错误的百分比减少程度不超过3%, 并且明显优于FTMES和SAMP 30%方法, 进一步说明IETCR方法能够精准定位被测程序中的错误, 具有一定的实用价值, 在错误定位领域, 能精确定位少量错误, 比模糊定位大量错误更具有实用意义. 表中使用Jaccard(JA)公式检查10%, 15%, 50%, 60%的代码时, IETCR方法定位错误的比例高于原始MBFL, 在错误定位精度方面有了一定提升.

图 4 MBFL约减方法错误定位精度比较

表 6 MBFL, IETCR, FTMES, SAMP 30%错误定位精度比较

EXAM threshold(%)	Original MBFL					IETCR					FTMES					SAMP 30%
EXAM threshold(%)	JA	OC	OP	TA	DS	JA	OC	OP	TA	DS	JA	OC	OP	TA	DS	JA	OC	OP	TA	DS
1	0.31	0.31	0.27	0.05	0.30	0.29	0.29	0.27	0.02	0.28	0.03	0.03	0.03	0.01	0.03	0.22	0.22	0.20	0.05	0.22
5	0.72	0.74	0.70	0.37	0.74	0.70	0.70	0.64	0.21	0.69	0.23	0.23	0.27	0.19	0.24	0.55	0.57	0.56	0.28	0.58
10	0.79	0.81	0.76	0.55	0.80	0.80	0.80	0.73	0.33	0.77	0.36	0.36	0.39	0.27	0.36	0.63	0.65	0.63	0.42	0.66
15	0.80	0.82	0.79	0.61	0.82	0.82	0.82	0.78	0.41	0.81	0.50	0.50	0.57	0.34	0.50	0.68	0.68	0.69	0.48	0.69
20	0.84	0.84	0.81	0.69	0.84	0.82	0.82	0.78	0.42	0.81	0.52	0.52	0.58	0.35	0.55	0.71	0.74	0.71	0.55	0.73
30	0.88	0.89	0.86	0.80	0.88	0.88	0.88	0.86	0.58	0.88	0.64	0.64	0.74	0.49	0.66	0.75	0.78	0.77	0.62	0.78
40	0.88	0.89	0.88	0.81	0.89	0.88	0.88	0.88	0.78	0.88	0.73	0.73	0.83	0.62	0.74	0.81	0.83	0.82	0.67	0.83
50	0.89	0.92	0.90	0.83	0.91	0.90	0.90	0.90	0.90	0.81	0.90	0.75	0.85	0.67	0.78	0.87	0.86	0.85	0.81	0.86
60	0.94	0.94	0.92	0.90	0.93	0.95	0.95	0.93	0.90	0.95	0.85	0.86	0.92	0.80	0.89	0.89	0.89	0.99	0.88	0.89
70	0.95	0.95	0.93	0.94	0.94	0.95	0.95	0.93	0.90	0.95	0.90	0.90	0.92	0.86	0.92	0.90	0.89	0.99	0.89	0.89
80	0.97	0.97	0.96	0.97	0.97	0.97	0.97	0.96	0.96	0.97	0.96	0.96	0.94	0.94	0.96	0.93	0.93	0.93	0.92	0.92
90	0.98	0.98	0.98	0.98	0.98	0.98	0.98	0.98	0.98	0.98	0.97	0.97	0.96	0.97	0.97	0.98	0.98	0.98	0.98	0.98
100	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00

表 6 MBFL, IETCR, FTMES, SAMP 30%错误定位精度比较

为了分析IETCR方法与原始MBFL, FTMES, SAMP 30%方法之间是否存在显著性差异, 本文在置信度为95%的水平下对上述方法进行了秩和检验(Wilcoxon signed-rank test), 试验结果如表7所示. 表中包括5个怀疑度公式, 每个对应的值包括两部分, 第一部分为对应方法在所有被测程序中EXAM Score的平均值, 括号中的值为对应方法与IETCR方法秩和检验的P-Values值. 加粗部分对应的P-Values值大于0.05, 表示对应方法与原始MBFL之间没有存在显著差异. 依据表中数据, IETCR方法与原始MBFL之间不存在显著性差异, 与FTMES, SAMP 30%方法(Tarantula公式除外)之间存在显著性差异

表 7 显著性分析

4.4.3 方法的影响因素

为探讨RQ3, 本文从计算测试用例信息熵的怀疑度公式和信息熵的计算过程出发, 讨论IETCR的影响因素和额外开销.

本节首先研究不同SBFL公式的定位效果, 并选择性能最优的怀疑度公式用于IETCR方法中测试用例信息熵的计算. 实验使用5种不同的SBFL公式, 对上述实验程序中的错误进行定位, 实验结果如表8所示. 表8列出了不同SBFL公式的EXAM Score值在不同检查比例下所占的百分比, 其中加粗部分表示使用对应怀疑度公式和检查比例, SBFL公式定位错误百分比的最大值. 从表中数据可知, 所有检查比例中, 使用Dstar(DS)公式均能定位最多的错误, 说明在上述SBFL公式中, Dstar(DS)的性能最优. 因此, 本文使用Dstar公式计算测试用例的信息熵.

表 8 SBFL方法错误定位精度比较

本节其次讨论IETCR的额外时间开销. 本文统计了该方法在实验程序上计算信息熵的时间开销, 如图5所示. 在图5中, 横坐标表示不同的实验程序, 纵坐标表示执行时间, 单位是秒, 图中每一部分表示IETCR方法在对应实验程序上计算全部通过测试用例的信息熵所花费时间的分布情况, 其中包括5个数值点, 从下到上依次为最小值, 下四分位数, 中位数, 上四分位数, 最大值.

由图5可知, IETCR方法在6个程序上测试用例的信息熵计算时间范围为20~800 s, 其中执行时间最少的程序是totinfo, 最大的程序是printtokens, 有3个程序的平均执行时间少于200 s, 相比IETCR方法约减的变异体执行开销, 这些额外执行时间是可以忽略不计的. 因此, IETCR有更好的约减效果, 同时伴随着少量测试用例信息熵的计算开销.

图 5 IETCR 方法额外执行开销

5 结论与展望

为了降低基于变异的错误定位技术的执行开销, 本文从测试用例角度, 提出了一种基于信息熵的测试用例约减策略IETCR, 利用信息熵理论对通过测试用例进行排序, 选择执行部分检错能力强的通过测试用例和所有失败测试用例, 有效减少了测试用例的数量, 同时保证了测试用例集的质量. 实验结果表明, IETCR方法能够约减56.3%~88.6%的执行开销, 而错误定位精度与原始MBFL技术没有显著性差异. 在后续的研究中, 作者将考虑扩大数据集来验证方法的有效性, 并结合基于机器学习的变异体执行结果预测方法, 在不执行变异体的前提下预测其被测试用例杀死与否的结果, 更进一步减少MBFL技术的执行开销.

参考文献

[1]	Shin D, Bae DH. A theoretical framework for understanding mutation-based testing methods. 2016 IEEE International Conference on Software Testing, Verification and Validation (ICST). Chicago, IL, USA. 2016. 299–308.
[2]	Howden WE. Theoretical and empirical studies of program testing. IEEE Transactions on Software Engineering, 1978, SE-4(4): 293-298.
[3]	Wong WE, Gao RZ, Li YH, et al. A survey on software fault localization. IEEE Transactions on Software Engineering, 2016, 42(8): 707-740.
[4]	Masri W. Fault localization based on information flow coverage. Software Testing, Verification and Reliability, 2010, 20(2): 121-147.
[5]	Keller F, Grunske L, Heiden S, et al. A critical evaluation of spectrum-based fault localization techniques on a large-scale software system. 2017 IEEE International Conference on Software Quality, Reliability and Security (QRS). Prague, Czech. 2017. 114–125.
[6]	Jones JA, Harrold MJ. Empirical evaluation of the Tarantula automatic fault-localization technique. Proceedings of the 20th IEEE/ACM International Conference on Automated Software Engineering. Long Beach, CA, USA. 2005. 273–282.
[7]	Papadakis M, Le Traon Y. Using mutants to locate “Unknown” faults. 2012 IEEE Fifth International Conference on Software Testing, Verification and Validation. Montreal, QC, Canada. 2012. 691–700.
[8]	Papadakis M, Le Traon Y. Metallaxis-FL: Mutation-based fault localization. Software Testing, Verification and Reliability, 2015, 25(5–7): 605-628.
[9]	Moon S, Kim Y, Kim M, et al. Ask the mutants: Mutating faulty programs for fault localization. 2014 IEEE Seventh International Conference on Software Testing, Verification and Validation. Cleveland, OH, USA. 2014. 153–162.
[10]	Pearson S, Campos J, Just R, et al. Evaluating and Improving Fault Localization. 2017 IEEE/ACM 39th International Conference on Software Engineering (ICSE). Buenos Aires, Argentina. 2017. 609–620.
[11]	Chekam TT, Papadakis M, Le Traon Y. Assessing and comparing mutation-based fault localization techniques. arXiv preprint arXiv: 1607.05512, 2016.
[12]	Mathur AP. Performance, effectiveness, and reliability issues in software testing. Proceedings the Fifteenth Annual International Computer Software & Applications Conference. Tokyo, Japan. 1991. 604–605.
[13]	De Oliveira AAL, Camilo-Junior CG, De Andrade Freitas EN, et al. FTMES: A failed-test-oriented mutant execution strategy for mutation-based fault localization. 2018 IEEE 29th International Symposium on Software Reliability Engineering. Memphis, TN, USA. 2018. 155–165.
[14]	Liu Y, Li Z, Zhao RL, et al. An optimal mutation execution strategy for cost reduction of mutation-based fault localization. Information Sciences, 2018, 422: 572-596.
[15]	Yoo S, Harman M, Clark D. Fault localization prioritization: Comparing information-theoretic and coverage-based approaches. ACM Transactions on Software Engineering and Methodology, 2013, 22(3): 19.
[16]	Papadakis M, Le Traon Y. Effective fault localization via mutation analysis: A selective mutation approach. Proceedings of the 29th Annual ACM Symposium on Applied Computing. New York City, NY, USA. 2014. 1293–1300.
[17]	Demillo RA, Lipton RJ, Sayward FG. Hints on test data selection: Help for the practicing programmer. Computer, 1978, 11(4): 34-41.
[18]	Offutt AJ, Untch RH. Mutation 2000: Uniting the Orthogonal. Wong WE. Mutation Testing for the New Century. Boston: Springer, 2001. 34–44.
[19]	Voas JM. PIE: A dynamic failure-based technique. IEEE Transactions on Software Engineering, 1992, 18(8): 717-727.
[20]	Chen MY, Kiciman E, Fratkin E, et al. Pinpoint: Problem determination in large, dynamic Internet services. Proceedings International Conference on Dependable Systems and Networks. Washington, DC, USA. 2002. 595–604.
[21]	Abreu R, Zoeteweij P, Van Gemund AJC. An evaluation of similarity coefficients for software fault localization. 2006 12th Pacific Rim International Symposium on Dependable Computing. Riverside, CA, USA. 2006. 39–46.
[22]	Naish L, Lee HJ, Ramamohanarao K. A model for spectra-based software diagnosis. ACM Transactions on Software Engineering and Methodology, 2011, 20(3): 11.
[23]	Jones JA, Harrold MJ, Stasko J. Visualization of test information to assist fault localization. Proceedings of the 24th International Conference on Software Engineering. Orlando, FL, USA. 2002. 467–477.
[24]	Wong WE, Debroy V, Gao RZ, et al. The DStar method for effective software fault localization. IEEE Transactions on Reliability, 2014, 63(1): 290-308.
[25]	Liu Y, Li Z, Wang LX, et al. Statement-oriented mutant reduction strategy for mutation based fault localization. 2017 IEEE International Conference on Software Quality, Reliability and Security (QRS). Prague, Czech. 2017. 126–137.
[26]	Shannon CE. A mathematical theory of communication. The Bell System Technical Journal, 1948, 27(4): 623-656.
[27]	Do H, Elbaum S, Rothermel G. Supporting controlled experimentation with testing techniques: An infrastructure and its potential impact. Empirical Software Engineering, 2005, 10(4): 405-435.
[28]	Yang Q, Li JJ, Weiss DM. A survey of coverage-based testing tools. The Computer Journal, 2007, 52(5): 589-597.
[29]	Delamaro ME, Maldonado JC, Vincenzi AMR. Proteum/IM 2.0: An integrated mutation testing environment. In: Wong WE, ed. Mutation Testing for the New Century. Boston: Springer, 2001. 91–101.
[30]	Le TDB, Lo D, Le Goues C, et al. A learning-to-rank based fault localization approach using likely invariants. Proceedings of the 25th International Symposium on Software Testing and Analysis. Saarbrücken, Germany. 2016. 177–188.
[31]	Li X, Zhang LM. Transforming programs and tests in tandem for fault localization. Proceedings of the ACM on Programming Languages, 2017, 1(OOPSLA): 92.
[32]	Wilcoxon F. Individual comparisons by ranking methods. Biometrics Bulletin, 1945, 1(6): 80-83.
[33]	Zhang LM, Marinov D, Khurshid S. Faster mutation testing inspired by test prioritization and reduction. Proceedings of the 2013 International Symposium on Software Testing and Analysis. Lugano, Switzerland. 2013. 235–245.