将C-V2X业务部署在MEC平台上, 可以更好地降低数据传输时延, 缓解基础设施的计算与储存压力, 降低大量数据回传所造成的网络负担, 提供高质量服务. 然而, 面对海量的数据和设备成本的考量, MEC边缘缓存节点的缓存容量有限, 使得合理部署缓存内容成为亟需解决的问题. 因此, 准确预测用户的内容需求将起重要作用.
据研究发现大部分用户请求的都是流行的文件[1,2], 少部分请求不流行的文件. 这一文件请求分布与Breslau等观察到的请求网页相对频率遵循Zipf定律[3]极为相似. 然而, 这一请求分布描述的仅仅为某一时刻的静态请求. 事实上, 大部分文件的热度会随着时间的推移逐渐减弱, 新内容的出现也会影响分布规律. 除此之外, 用户往往更加青睐于点击请求自己感兴趣的文件[4], 所以流行度分布的影响面极广, 具有动态性[5,6]. 进一步的研究表明, 网络中用户的前后访问行为有一定的时间间隔[7], 针对这一特点, 科研人员在研究用户请求部分中加入了请求生成时间间隔服从泊松分布或固定值. 不可否认的是, 这一改变增强了研究的可靠性, 但在请求前后时间间隔方面, 泊松分布的适用性还有待研究.
在预测用户请求方面, 线性回归进行预测[8,9]的研究占据相当大的比例, 但由于在预测过程中存在不可测因子的影响, 使其实用性受到一定限制. 考虑到偶然因素造成的影响, 常运用短中长期预测的时间序列预测法. 长短时记忆网络(LSTM)是当前比较流行的深度学习模型之一, 它类似于一个记忆器, 模拟了人类的认知过程, 能较好地运用于文件请求流行度的预测[10].
综上, 本文将针对C-V2X的城市场景, 以基站作为MEC边缘缓存节点, 根据大量用户请求, 探索出基站处文件流行请求规律, 实现流行文件在基站处的预测和缓存有效减少数据传输时延等阻塞问题.
1 基于SUMO的城市场景交通流模型以福州地图为例, 设定了四纵四横的车联网. 为了更贴近实际交通情况, 记录了福州早晚高峰路口处红绿灯时长、车流量和地面可行驶方向等相关数据, 同时在福州交警软件上进行实时观测. 最后, 介绍输出数据文件, 并进行简化处理. 需要说明的是, 预测模型是数据驱动, 在不同的城市场景下, 可通过重新构建请求的训练数据提升预测模型的适应性, 但并不影响本文所提出研究方法的通用性. 另外, 预测模型可部署为在线学习模式, 在深夜等车流量很少的时段通过数据统计算法重构数据集并完成模型训练.
1.1 网络构建为模拟早晚高峰时间段的交通流情况, 设置两个早高峰驶出口, 两个晚高峰驶出口. 基站则布置在纵横四条路段的中间位置, 在基站数量最少的情况下覆盖整个交通网络. 交通地图如图1所示, 其中, L/R-2-*及U/D-*-2为交通网的主干道, 其余为辅道, 各路段名称、行驶方向、基站及基站覆盖范围均已标出.
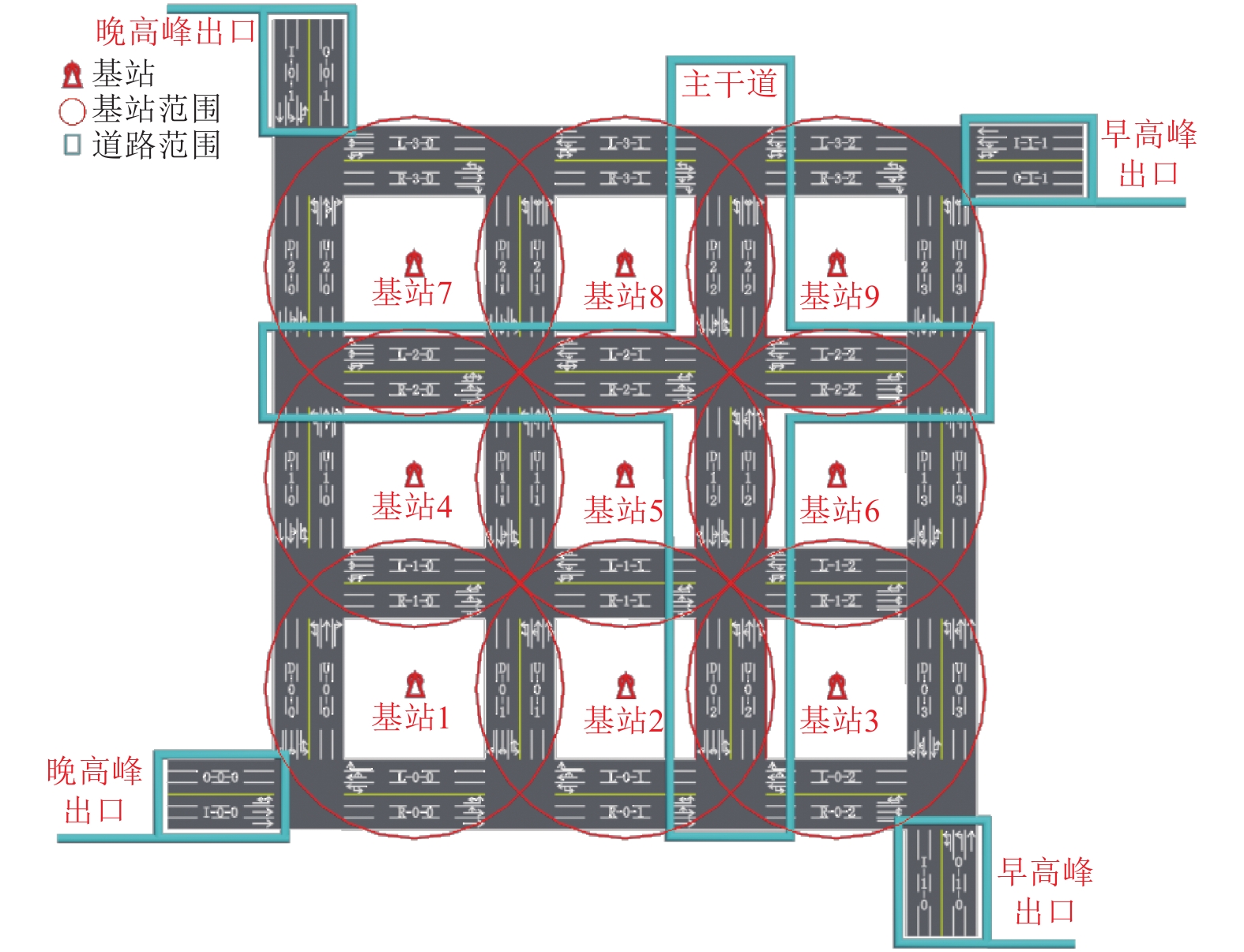
|
图 1 交通流网络 |
1.2 车流轨迹建模
通过实地考察, 对福州的上浦路口、浦上大道、南门兜附近路口和宝龙广场附近路口等位置的早晚高峰红绿灯时长、车道地标转向和车流量进行了实时记录. 并且在周一至周五早晚高峰期间, 参考福州交警软件, 观察各路段的交通堵塞状况和路口车流量状况. 在红绿灯时长方面, 对于车流量多的方向, 信号灯通常设为80 s到95 s; 对于车流量较少的方向, 信号灯通常设为30 s到45 s; 警示信号黄灯为3 s到5 s. 车流量部分记录结果如表1所示. 综合以上考察, 共同设定SUMO软件[11]的仿真参数.
1.3 数据输出及预处理在SUMO的输出文件中, fcd.xml文件包含时间、车辆名称、车辆位置、车辆速度和车辆所在道路等重要数据, 故最终选择fcd.xml文件作为输出使用, 并进行了数据预处理, 如程序结构1所示. 由于fcd.xml文件过大不能一次性读入, 则将fcd.xml文件切分成32个62 MB左右且与原文件结构一致的小文件, 依次经过Matlab处理, 形成一个包含车辆名称、坐标、速率及道路信息的TXT文件.
| 表 1 福州路口车流量记录 |
算法1. XML转TXT
输入: 切分后的XML文件
输出: TXT文件
1. for 32个XML文件 do
2. node←读取各节点
3. timenode_num←时间节点数量
4. for 时间节点数量 do
5. vehiclenode←车辆节点
6. txtarray(1)←当前时间属性
7. vehiclenode_num←车辆节点数量
8. for 车辆节点数量 do
9. txtarray(n)←当前车辆信息属性 (n为信息数量)
10. for n do
11. fprintf←信息依次写入txt
12. end for
13. end for
14. end for
15. clear←清空所有已读取的节点
16. end for
2 文件请求模型及预测文件流行度变化具有时变性, 请求间隔也存在一定规律. 为了改善分布模型中缺乏文件流行度实时性的弊端, 对网易新闻进行实时数据采集. 根据车流量趋势来合理分配流行度分布, 利用LSTM模型能利用历史信息较好预测的优势, 将其作为深度学习预测模型.
2.1 数据采集考虑到文件流行度具有时变性和请求之间存在间断性的特点, 在请求间隔方面, 本文通过统计用户浏览文件的逗留时间, 利用Matlab拟合出请求间隔分布. 在文件流行度方面, 参考国内各大音乐、新闻、社交等网站, 发现大部分网站存在一定的不适用性. 例如, 信息更新状态时间跨度太长, 信息数量较少、种类单一, 大部分信息无法长期跟踪统计, 在统计播放量、阅读量等可利用值时, 无法精确到个位数乃至千位数, 导致结果不准确, 页面复杂程度较高, 数据在短时间内无法爬取完成, 导致数据之间存在时间差, 真实性下降. 综合评估后, 本文采用八爪鱼采集器收集网易新闻的数据集. 网易新闻是国内第一新闻客户端, 具有实时性、分类合理性、数据量多和易采集的特性. 数据采集过程中, 自定义模板流程如图2所示, 详细配置后, 每个小时执行一次.
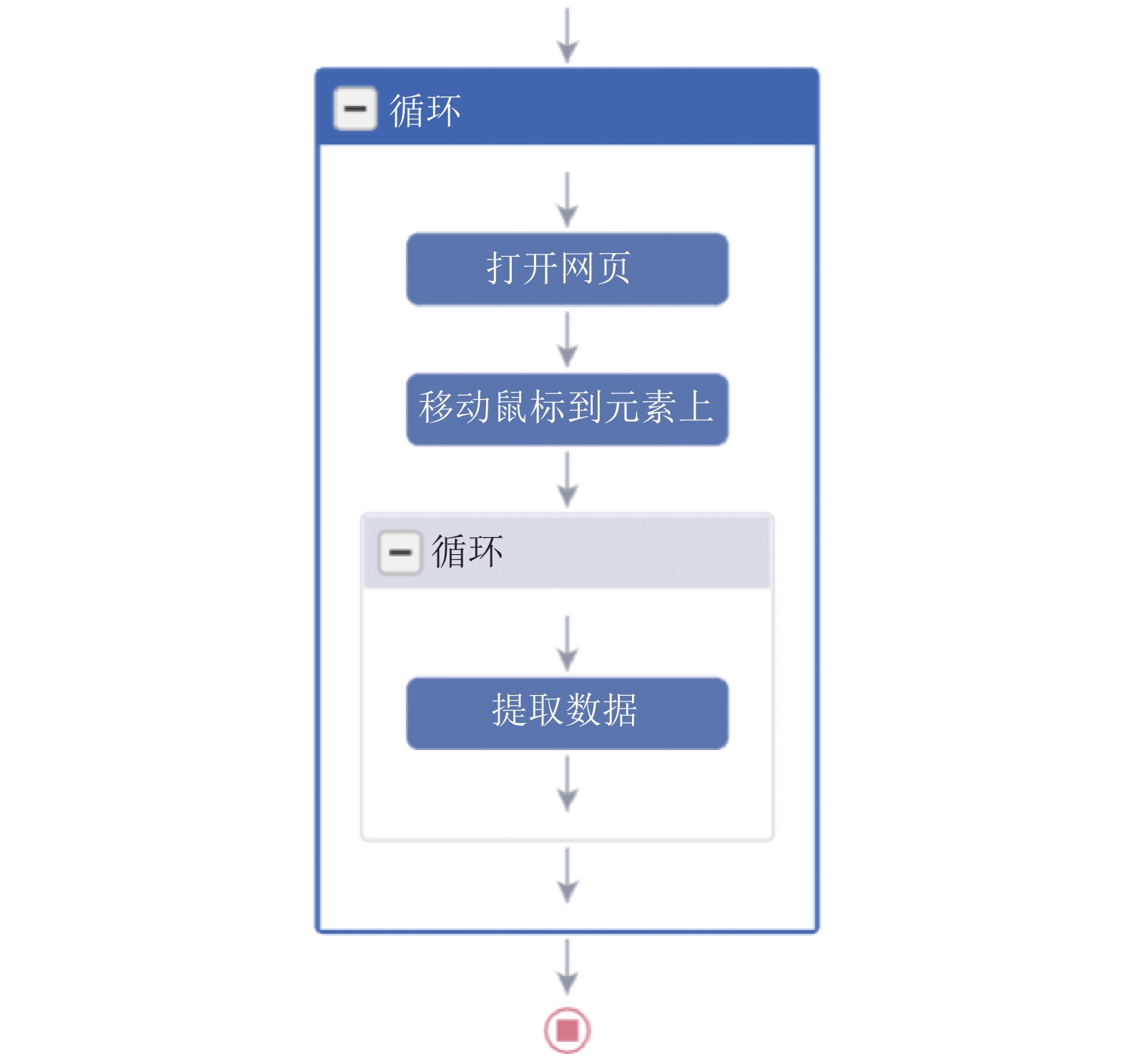
|
图 2 采集模板 |
在采集到的数据集中, 有11种类型, 共2116条内容. 对于具体类型和内容, 先筛选所有在24小时内出现过的内容进行合并内容处理, 其中某些时段因浏览量较少而无法进入排行榜的内容, 对应时段的点击量记为零. 因日常生活车辆用户请求与车流量变化密切相关, 本文对两者分别进行仿真统计, 并对比趋势进行相应数据集筛选匹配. 仿真车流量如图3所示, 点击量的统计结果如图4所示.
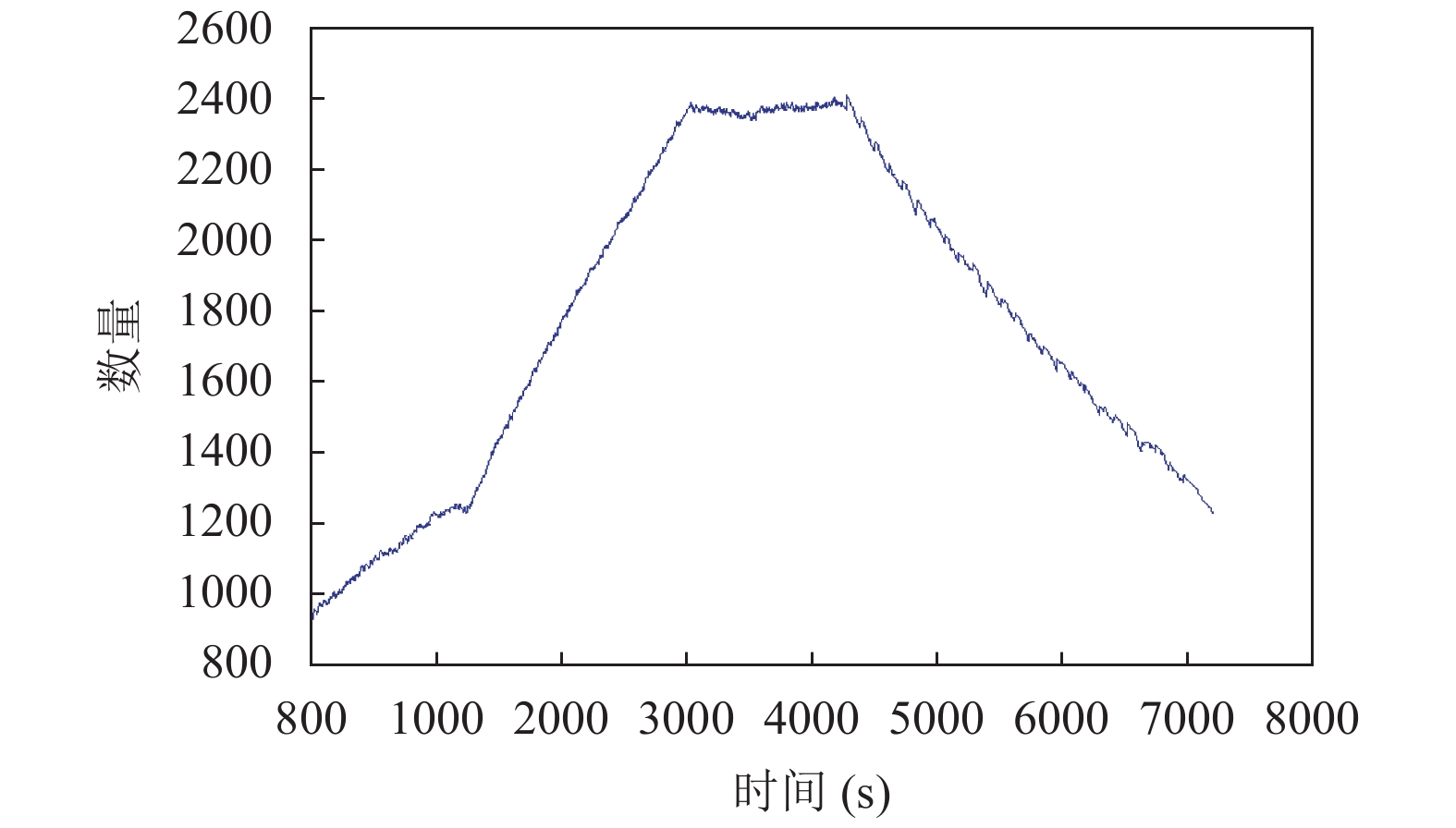
|
图 3 车流量 |
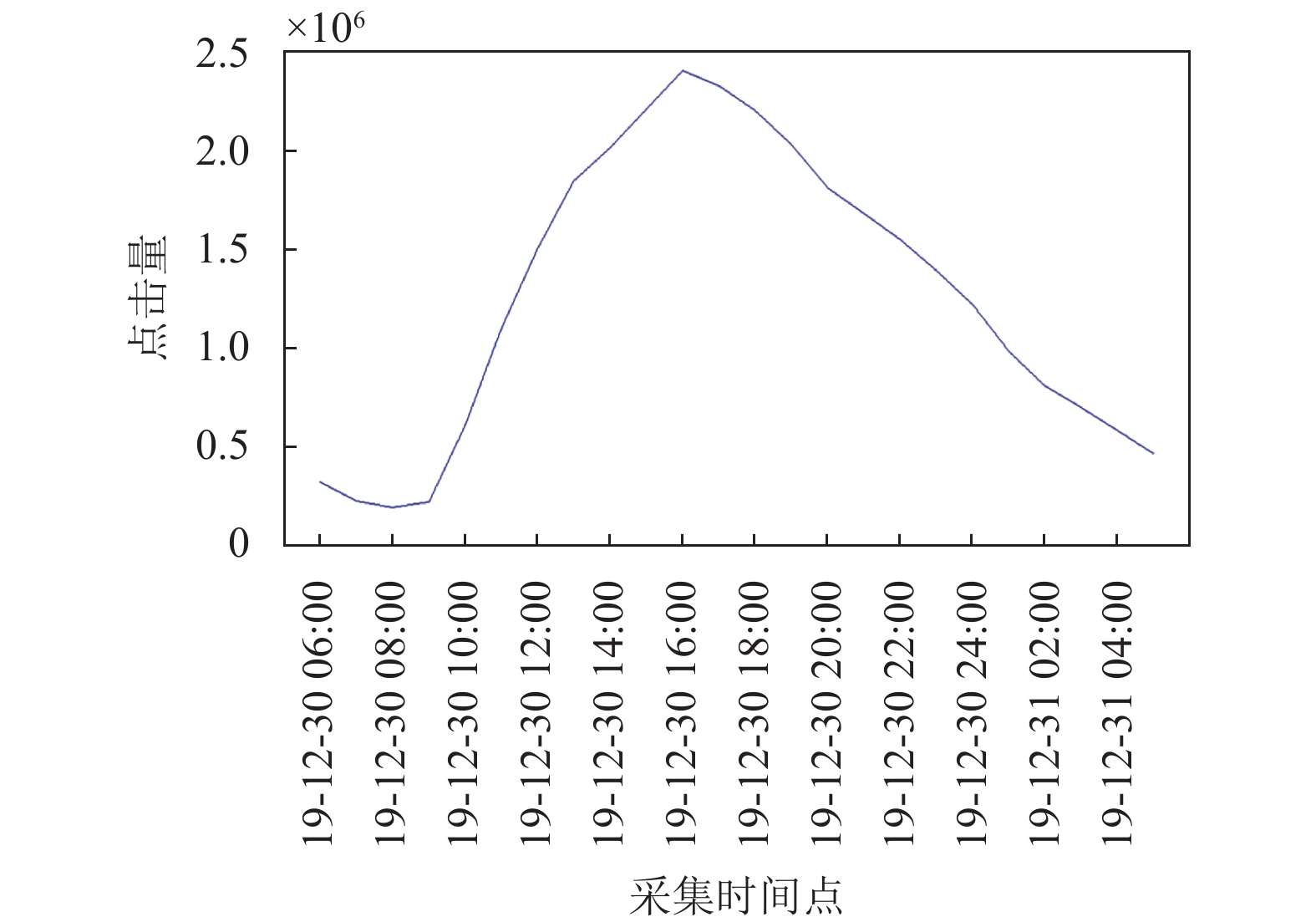
|
图 4 各时间段总点击量 |
2.2 文件请求生成
车辆在运动过程中服从相应时段的请求分布, 实现如算法2. 在传输过程中, 文件被切割为若干块, 块之间传输需要一定的时间间隔, 因此设定在请求间隔内, 用户对某个文件的请求是唯一不变的. 具体请求生成方式如下, 根据收集到的数据集, 将流行度分为15个时间段, 而每一时间段的请求分为11种不同的类型, 每个类型包含若干文件. 车辆生成请求时, 根据其所在的时段对应的流行度分布, 利用请求类别概率得到请求所属类别, 再根据该类别中各文件在该时刻的历史平均请求概率生成最终请求. 因此, 将类别和文件的相关性以概率的方式呈现. 为减少偶然性, 采用每辆车请求20次的平均值.
算法2. 车辆文件请求及接收
输入: TXT文件、文件流行度、请求间隔分布
输出: 各基站各个时间点接收各文件的频数
1. BaseStationaddress←定义基站位置
2. vehiclename←所有出现过的车辆名称
3. requestcount←车辆请求间隔计数器
4. p←导入请求间隔分布
5. sort_p←导入类型文件流行度分布
6. probability_n←导入流行度分布 (n为类型编号)
7. while TXT文件读取结束do
8. while 当前时刻结束 do
9. xArray(m)、yArray(m)、nameArray(m)←车辆位置及名字(m为车辆数目)
10. end while
11. popular_interval←当前时间对应的流行度分布
12. request.count=request.count-1→计数器减一
13. for m do (m为车辆数目)
14. tablepos←锁定车辆在计数器中的位置
15. if 车辆计数器等于0或出现的新车辆 then
16. request(tablepos,2).count←按请求间隔分布生成请求间隔
17. sortrequest, beforerequestsort←按类型流行度分布生成请求并记录
18. filerequest, beforerequestfile←按内容流行度分布生成请求并记录
19. BaseStationnum←车辆在几号基站范围
20. if 在接收范围 then
21. BaseStation←对应基站数组记录
22. else
23. contitune;
24. end if
25. else
26. BaseStationnum←车辆在几号基站范围
27. if 在接收范围 then
28. BaseStation←对应基站数组记录
29. else
30. continue;
31. end if
32. end if
33. end for
34. end while
2.3 基于LSTM的文件请求预测LSTM是为了解决RNN训练过程中梯度消失问题而提出的, 其中vanilla LSTM是当前应用最为广泛的一种LSTM模型[12]. 在文中则直接利用基本的vanilla LSTM来构建预测模型, 算法3实现.
算法3. VanillaLSTM预测
输入: 基站接收的需求序列
输出: 预测序列
1. import程序中用到的包
2. forward, look_back, epoches←定义预测步长、回溯时间和训练次数
3. for 类型数量 do
4. dataset←读入基站接收需求序列
5. def creat_dataset←定义分割数据的函数
6. for 序列长度减5 do
7. dataX.append,dataX.append←分别追加相应的元素
8. return 返回分割好的数组数据
9. end def
10. numpy.random.seed(7) (生成随机种子)
11. scaler.fit_transform←将数据缩小到0–1之间
12. train_size←定义训练集大小
13. train,test←将数据集切分为训练集和测试集
14. look_back←定义前瞻步长
15. creat_dataset←分割训练集和测试集
16. trainX←重新设置数据格式
17. model←构建LSTM网络
18. model.fit←带入训练集进行训练学习
19. forward←定义预测步长
20. for 预测步长 do
21. predict←预测一步
22. result←累加记录预测一步的结果
23. train_pred←前一位剔除, 补新预测结果
24. end for
25. scaler.inverse_transform←将预测结果正则化
26. rmse←计算真实值与预测值的误差
27. plot←预测效果可视化
3 文件请求预测的仿真及分析在前述车流信息基础上, 对实时采样的交通网络文件进行详细的参数设置. 根据车流量与用户请求量的相关性, 对数据集进行筛选处理, 建立时变型类型流行度和文件流行度分布, 作为用户请求的依据. 在预测方面, 设置若干个回溯时间长度, 通过均方根误差的对比及分析, 选择出预测效果较好的参数值作为最终预测模型参数.
3.1 仿真参数设置 3.1.1 交通网络参数设置本文设置交通网如图1所示. 除出口路段外, 每条道路长度为1千米. 道路的转弯率规则则按照出口方向进行调整, 再结合早高峰特点, 则车辆向右行驶几率更大, 且在主干道行驶几率更大. 在路口中, 绿灯的时长往往根据车流量进行设置, 对于车流量较多的道路, 绿灯时长更长, 黄灯警示时间也相对略长. 反之亦然, 具体参数如表2所示.
在SUMO中, 根据表2进行参数设置, 并在SUMO-GUI中运行. 以节点11为例, 在仿真时间为25分12秒时的仿真画面效果如图5所示.
3.1.2 数据集筛选由于文件流行度具有时变性, 则按照不同时段内的文件流行度总点击量与车流量趋势进行对比排列. 实际采样中, 以小时为单位进行流行度采样, 采样时间为24小时.
由于流行度变化和车流量趋势的契合需要, 则适当缩短文件流行度的持续时间, 使其范围为早晚高峰两小时. 最终筛选数据集时间为12月30号早10点到晚12点. 在早高峰最大车流量稳定阶段, 选取点击量最大的数据集进行匹配, 其余数据集匹配则尽可能均匀分布. 将车流量和总点击量归一化处理后, 进行对应排列的结果如图6所示.
| 表 2 SUMO仿真参数 |

|
图 5 SUMO仿真场景 |
为了生成不同时段的新闻类型流行度分布和文件流行度分布, 分别求出不同类型不同时间段下的类型请求概率和文件请求概率, 如式(1)所示.
| ${P_{t,i}} = \frac{{{d_{t,i}}}}{{{D_t}}}\;\;$ | (1) |
| ${p_{t,i,j}} = \frac{{{s_{t,i,j}}}}{{{d_{t,i}}}}$ | (2) |
其中, Pt,i是第t个时间段, 第i种类型的请求概率, pt,i,j是第t个时间段, 第i种类型中第j条文件的请求概率, Dt是第t个时间段的总点击量, dt,i是第t个时间段的第i种类型的点击量, st,i,j是第t个时间段, 第i种类型中第j中文件的点击量.

|
图 6 场景内全部车流量与点击量的匹配 |
为了方便统计, 将类型和文件分别进行编号处理. 由于不同类型的请求概率变化细微, 且在不同时间段下变化趋势一致. 选择3个时间段的请求概率进行展示, 如图7所示. 其中新闻类型下, 部分文件在各个时间段内的请求概率如图8所示. 由图可得, 文件流行度具有时变性.

|
图 7 类型请求概率 |
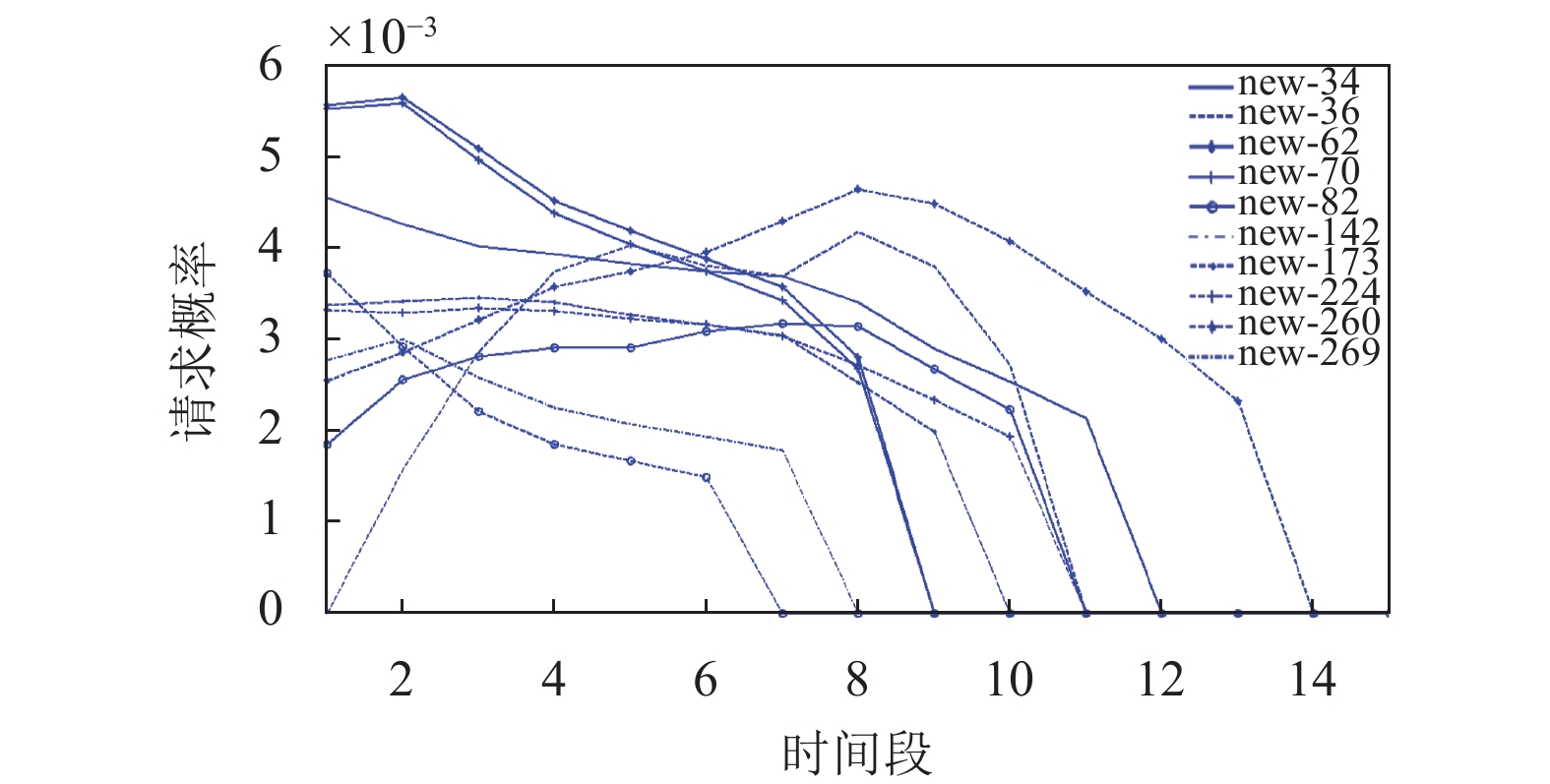
|
图 8 新闻类部分文件请求概率 |
3.2 仿真结果分析 3.2.1 SUMO仿真结果
设置参数是否符合实际早高峰场景是我们要考量的问题之一, 即主干道车流量与普通辅道车流量关系、出口处车流量与总体车流量、大部分路口峰值是否唯一等设置. 为了可以直观看出, 对full.xml输出文件进行数据处理, 如图3所示为总体车流量趋势图, 通过观察趋势可了解到, 总体仿真时间内只有一个峰值, 且峰值有一定的持续时间, 比较符合早高峰的趋势.
如图9所示, 大部分向出口方向行驶的路段车流量相对较多, 且有一个峰值. 而对于主干道ER21和EL21而言, 是交通场景中拥堵最严重的地方, 车流相对稳定且多, 一定程度上模拟了极为拥堵的场景. 如图10所示, 因主干道位置偏上, 导致部分检查路口向上车流量明显多余向下, 小部分交叉口反之. 同时可明显看出, 曲线均有不同程度的波动, 这是由路口红绿灯导致的车流局部堆积与流动.
3.2.2 VanillaLSTM模型预测及结果这一部分中, 本文基于vanillaLSTM模型, 采用多步预测的方式. 在Keras深度学习框架中, 通过构建Keras Sequential的顺序模型进行预测分析. 模型结构如图11所示, 由LSTM层和全连接层两个模型层堆叠而成. 其中, LSTM层返回维度为4的向量序列, 全连接层返回最后预测的单个结果. 选择均方误差RMSE为损失函数loss, adam为优化器. 在模型训练中, 由于数据量较少, 将所有的样本做为一个batch, epoch设为30次进行迭代, 得到最优权重分布的模型. 同时为了评估vanillaLSTM模型的性能, 本文选取67%的训练集供模型训练, 通过设置回溯时间长度为5到150的范围, 其中前30的间隔差距为5, 后120的间隔差距为10, 来预测未来20秒平均请求次数.
基于以上参数设置, 本文采用通过计算比较9个基站预测均方根误差的方式, 筛选出预测效果较好的参数, 得到的误差是在概率意义下均方误差最小. 考虑到请求基数的大小会对均方根误差的比较产生一定的影响, 故本文只选取请求概率在所有类型中居中的娱乐类型计算所得的均方根误差来作为比较标准, 结果如图12所示. 其中, 横向为各个回溯时间长度, 纵向为均方根误差.
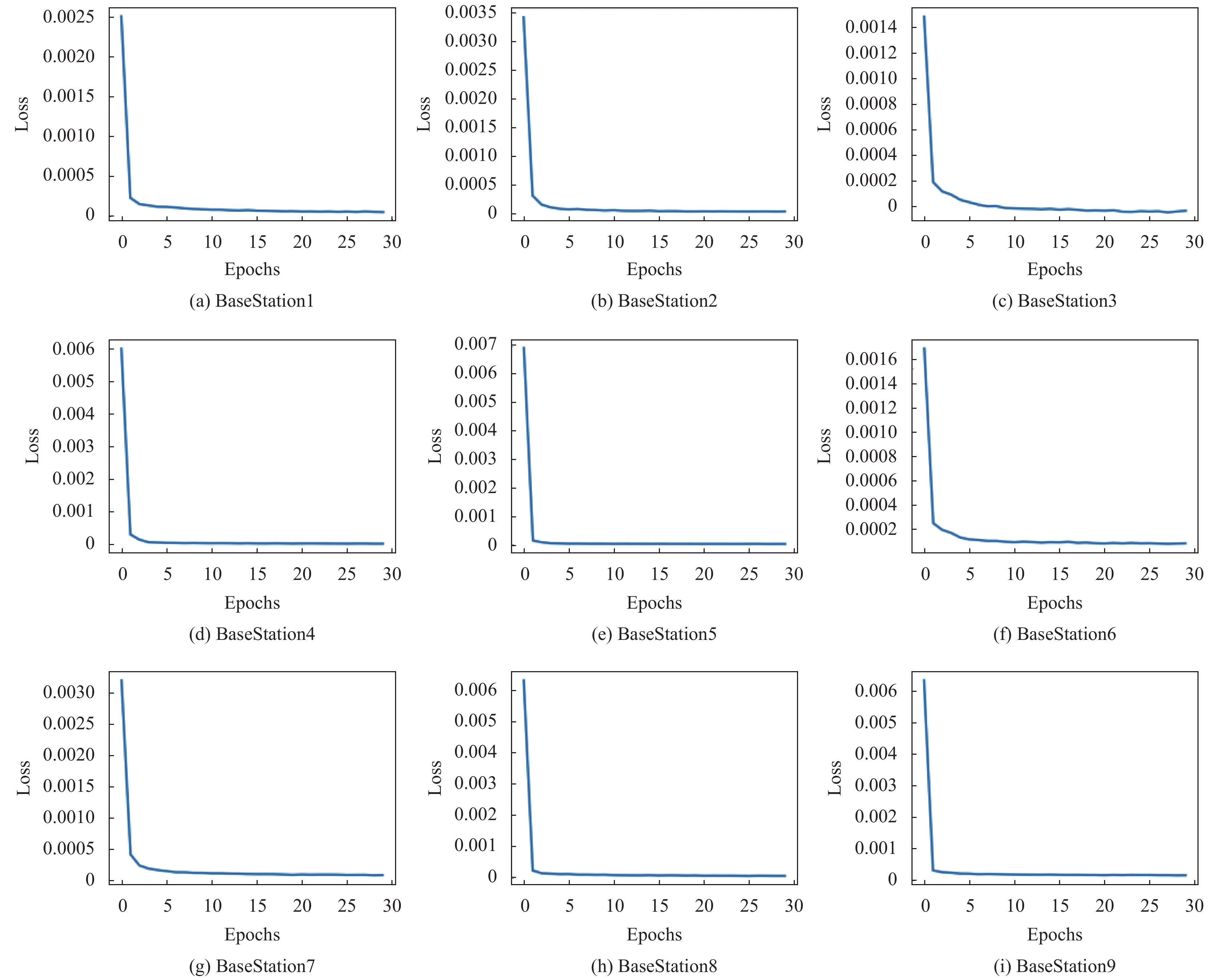
由图12可以看出, 当回溯时间长度为15时, 各基站间的均方根误差较小, 且整体水平处于较低的位置. 且如图13所示, 基站一到基站九的预测loss值收敛较快, 故设置回溯时间长度为15, 预测长度为20对基站类型文件进行预测. 对比下, 二号基站具有位置优势, 则二号基站娱乐类型预测结果如图14所示. 其中, 横向显示的是预测点前后共300秒的范围, 纵向是类型请求频数.
|
图 13 娱乐类型数据集训练loss曲线 |
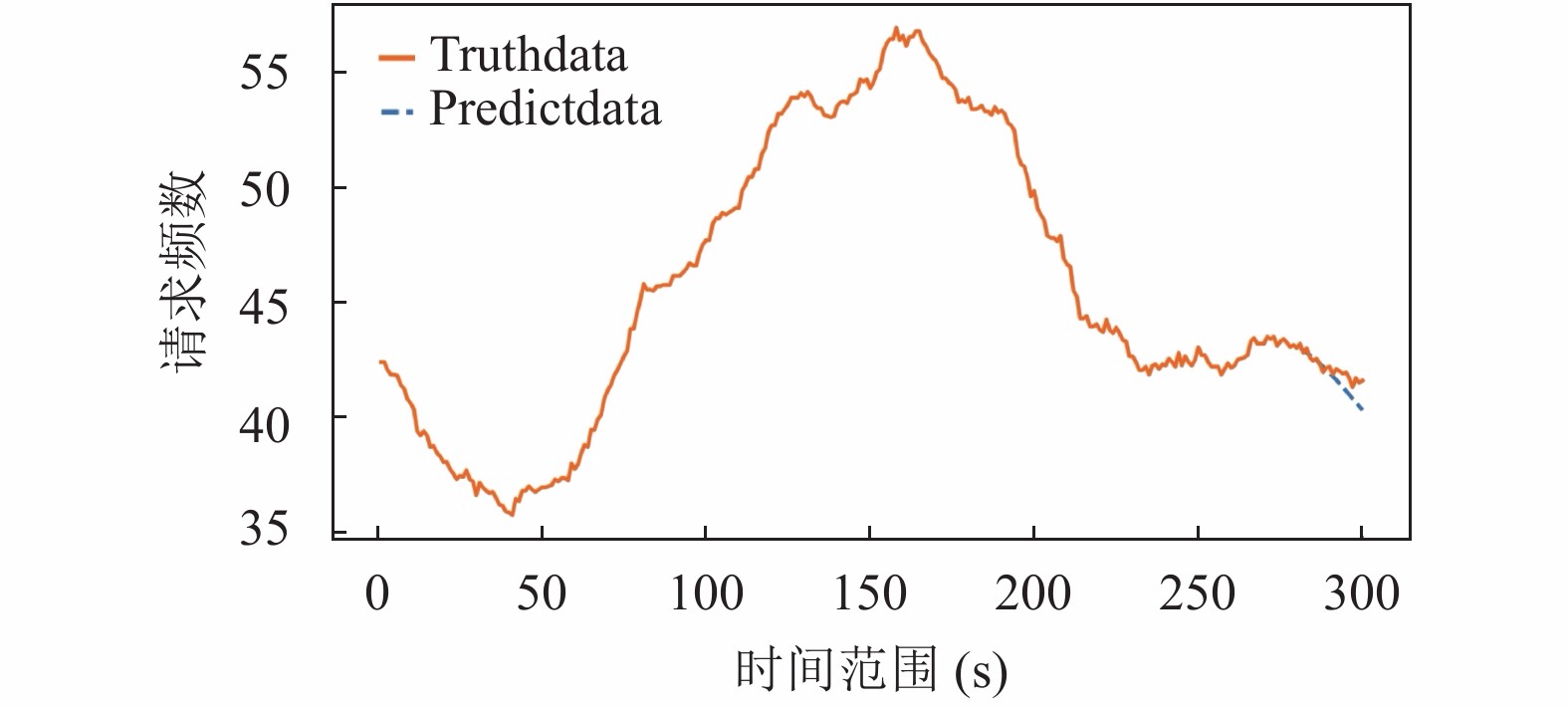
|
图 14 基站2中娱乐类型的预测结果 |
其他各基站各类型的预测结果均由计算统计均方根误差的形式呈现. 如图15所示. 以以基站为基准, 统计类型均方根误差的基站-类型统计时, 会因请求基数大小产生一到两个较大误差值, 如新闻和体育这类请求频率较大的类型. 整体误差分布较为均匀. 同理, 以类型-基站统计时, 请求基数会造成影响, 与图7相比, 类型变化趋势较为一致.
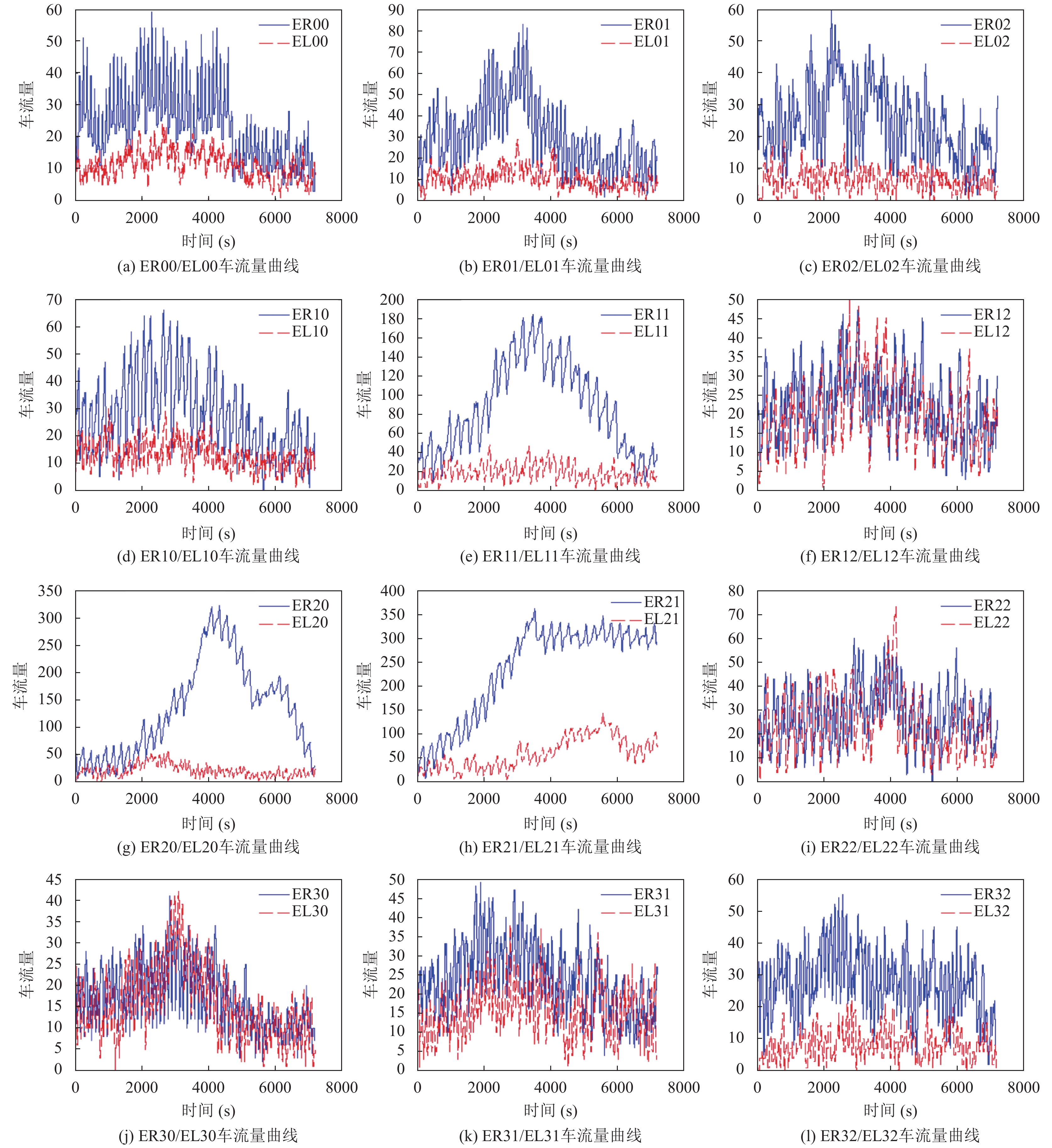
|
图 9 R/L方向车流量 |

|
图 10 U/D方向车流量 |
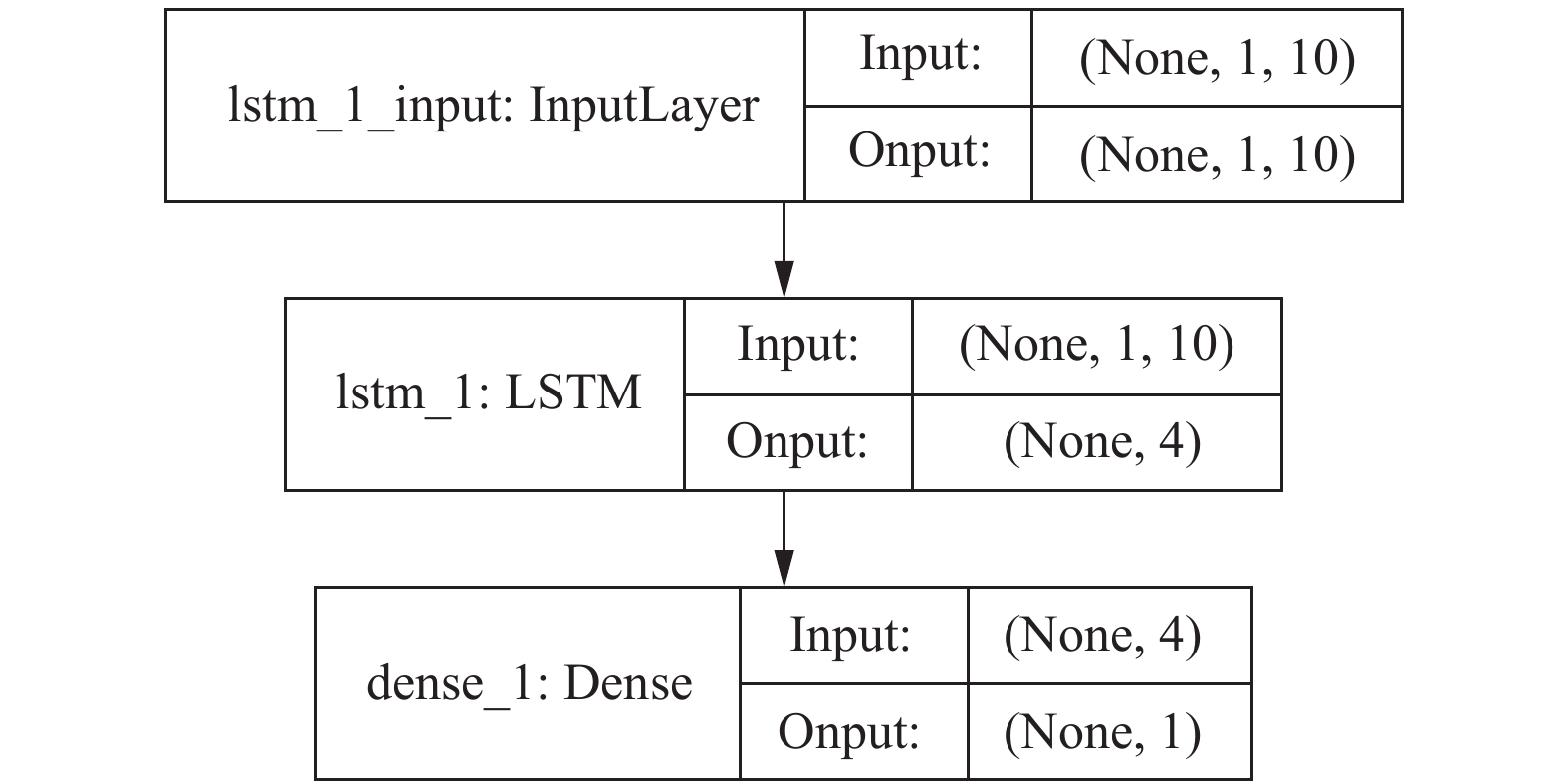
|
图 11 模型结构 |

|
图 12 不同look_back中娱乐类型的RMSE值 |
4 总结
文章从文件请求的时变性和时间间断性两个角度出发. 首先, 通过实地考察记录真实数据和参考权威软件的探测值, 利用SUMO仿真平台搭建出贴合现实的交通场景; 其次, 利用八爪鱼采集网易新闻数据集, 对数据处理后生成文件请求分布; 最后, 选取预测精度高且可以长期跟踪内容的LSTM深度学习模型进行预测. 后续研究将进一步细化文件相关性的影响, 并区分行人和车辆等不同用户类型.

|
图 15 各基站中对所有类型预测的RMSE值 |
| [1] |
Bastug E, Bennis M, Debbah M. Living on the edge: The role of proactive caching in 5G wireless networks. IEEE Communications Magazine, 2014, 52(8): 82-89. DOI:10.1109/mcom.2014.6871674 |
| [2] |
Liu A, Lau VKN. Cache-enabled opportunistic cooperative MIMO for video streaming in wireless systems. IEEE Transactions on Signal Processing, 2014, 62(2): 390-402. DOI:10.1109/tsp.2013.2291211 |
| [3] |
Breslau L, Cao P, Fan L, et al. Web caching and Zipf-like distributions: Evidence and implications. Proceedings of 18th Annual Joint Conference of the IEEE Computer and Communications Societies. New York, NY, USA. 1999. 126–134.
|
| [4] |
Shan Y, Liu TY, Liu H. Popular or personal: Access patterns of user generated content. 2010 First International Conference on Networking and Distributed Computing. Hangzhou, China. 2010. 367–371.
|
| [5] |
Qi KQ, Han SG, Yang CY. Learning a hybrid proactive and reactive caching policy in wireless edge under dynamic popularity. IEEE Access, 2019, 7: 120788-120801. DOI:10.1109/ACCESS.2019.2936866 |
| [6] |
Mehrizi S, Tsakmalis A, Shahbaz Panahi S, et al. Popularity tracking for proactive content caching with dynamic factor analysis. 2019 IEEE/CIC International Conference on Communications in China (ICCC). Changchun, China. 2019. 875–880.
|
| [7] |
廖一鸣. Web存储与用户行为分析研究[硕士学位论文]. 北京: 华北电力大学, 2016.
|
| [8] |
Zhang W, Wu D, Yang WD, et al. Caching on the move: A user interest-driven caching strategy for D2D content sharing. IEEE Transactions on Vehicular Technology, 2019, 68(3): 2958-2971. DOI:10.1109/TVT.2019.2895682 |
| [9] |
Zeng M, Lin TH, Chen M, et al. Temporal-spatial mobile application usage understanding and popularity prediction for edge caching. IEEE Wireless Communications, 2018, 25(3): 36-42. DOI:10.1109/mwc.2018.1700330 |
| [10] |
Sun M, Chen HP, Shu BQ. Predict-then-prefetch caching strategy to enhance QoE in 5G networks. 2018 IEEE World Congress on Services (SERVICES). San Francisco, CA, USA. 2018. 67–68.
|
| [11] |
Lopez PA, Behrisch M, Bieker-Walz L, et al. Microscopic traffic simulation using SUMO. 2018 21st International Conference on Intelligent Transportation Systems (ITSC). Maui, HI, USA. 2018. 2575–2582.
|
| [12] |
Greff K, Srivastava RK, Koutnik J, et al. LSTM: A search space odyssey. IEEE Transactions on Neural Networks and Learning Systems, 2016, 28(10): 2222-2232. DOI:10.1109/tnnls.2016.2582924 |
 2020, Vol. 29
2020, Vol. 29



