软件授权是指软件开发者利用相关加密算法及计算机技术来维护软件知识产权, 增加软件被恶意复制盗用的难度、延长软件被暴力破解的时间的一种技术手段^[1]. 利用软件授权来控制用户对软件的使用是目前维护软件知识产权最普遍的方式. 随着互联网技术的发展, 计算机软件与人们日常生活的联系越来越紧密, 伴随而来的软件知识产权保护问题也越来越重要^[2]. 目前互联网上已经出现很多未授权用户可以非法使用软件甚至恶意复制软件的行为, 说明软件授权的安全性还有待提高. 为了防止软件被恶意复制及非法盗用, 针对软件授权的安全问题, 提出一种新的软件授权加密方法即DPAPI加密算法与RSA数字签名算法混合的加密算法. 为以后软件授权技术的研发提供一个新的授权思路, 进一步提高软件授权过程中的安全性.

1 DPAPI加密算法

DPAPI (Data Protection API)是Microsoft随Windows操作系统一起提供的对数据进行加解密的一种特殊保护接口, 又称为数据保护应用程序编程接口^[3], 具有快速加密解密, 不用管理密钥, 防止离线暴力破解等优点. DPAPI加密算法提供两种加密机制, 分别是加密内存流机制和加密硬盘数据机制^[4]. 本文采用第二种加密机制. DPAPI加密算法的硬盘数据加密机制由加密函数CryptProtectData()和解密函数CryptUnProtectData()进行实现^[5], 且其与Windows系统用户紧密关联. 若用系统用户调用加密函数, 则加密后的数据只能由调用加密函数的同一系统用户进行解密, 且系统用户不能调用解密函数解密其他系统用户的DPAPI加密数据^[6], 这也是DPAPI加密算法能防止离线暴力破解的原因. 本文也是利用DPAPI加密算法的这一特性作为软件是否正确授权的参考. DPAPI加密算法的流程如图1所示.

2 RSA数字签名算法

RSA加密算法是目前应用广泛、影响较大的公钥密码算法^[7], 它能抵抗迄今为止已知的大多数密码攻击,已被ISO推荐为公钥数据加密标准^[8]. 其安全性是基于数论中大整数(两个素数的乘积)因式分解的困难程度, 即素数取值越大, 对大整数做因式分解的难度就越高, 密钥破解难度相对也就越大, 算法也就更安全. 换一句话说, 分解大数因式愈困难, RSA算法也就愈安全. 除此之外, RSA算法的通信双方不需要提前传递密钥, 安全性能高, 且其数学原理简单, 在工程应用中比较容易实现, 既可以用来对数据进行加密又可以用来对信息发送方进行身份的认证, 常与其他加密算法结合使用.

RSA数字签名算法是经由RSA公钥密码算法发展而来的^[9], RSA数字签名算法使用私钥对数据进行签名(也可称之为加密), 使用公钥对数据进行验证(也可称之为解密), 如图2所示. 进行RSA数字签名有以下3种目的, 一是为了确定接收方接收的数据确实是由发送方对数据进行签名并发送的, 即发送方身份认证. 二是经过数字签名的数据可保证自身的数据完整性, 即不可篡改伪造. 三是数据经过数字签名之后, 发送方不能拒绝承认数据及签名是己方发送的, 即不能抵赖不承认. 因为数字签名的特性就是表征数据特点的, 如果数据被篡改或伪造, 同样也会致使签名的更改, 不同的数据将得到不同的签名结果(因签名是私钥及哈希加密数据后的结果), 所以数字签名在保证数据的安全、完整及真实性等方面有着非常重要的作用. 对数据进行RSA数字签名的过程^[10]如图2.

(1)生成密钥: (发送方即服务器端)取大素数p和q, 两者互质且保密; 计算大整数 ${{n}} = p*q$ 及欧拉函数 $\varphi (n) = (p - 1)*(q - 1)$ ; 取整数e,使得e满足条件 $1 < e < \varphi (n)$ , 且 $(\varphi (n),e) = 1$ ; 再取e的逆元为d, 使得 $d = {e^{ - 1}} ({\rm{mod}}\; \varphi (n))$ ; 取(e,n)为公钥, (d,n)为私钥.

(2)签名: 服务器端发送签名消息M到客户端, 先计算 $S = Sig(M) = {M^d}({\rm{mod}}\; n)$ 再将S作为服务器端的数字签名附加到消息M上.

(3)验证: 若客户端(即接收方)需要验证服务器端对消息M的数字签名S,则计算: $M'{\rm{ = }}{{{S}}^{{e}}}({\rm{mod}}\; n)$ , 比较M'与M是否相等, 若 $M' {\rm{ = }}M$ , 则表明签名S确实是服务器端对消息M的签名, 否则签名S不是由服务器端生成的, 是伪造的.

3 DPAPI与RSA混合加密算法 3.1 DPAPI与RSA混合加密算法的提出

从Windows 2000到更高版本的操作系统中都提供DPAPI加密算法, 用户或操作系统程序都可以直接调用DPAPI接口函数来对数据进行加密解密. 由于DPAPI加密算法具有简单易用、加密强度大、不用管理密钥(操作系统管理密钥)的特性使得大量应用程序都采用DPAPI加密算法来加密用户的重要数据. 如远程桌面及IE浏览器的自动登录密码、邮箱(Outlook)账号密码等^[6]. 其次在进行DPAPI加密的过程中, 若加密之前与计算机关联, 并使用用户口令或计算机凭据加密数据, 则解密操作只能在实施加密操作的计算机上执行, 即使传输的数据被拦截, 第三方也很难实现离线的暴力破解^[4]. 最后, DPAPI加密算法的内部结构及操作原理一直处于封闭状态并未在微软官方公布, 这也在一定程度上保证了DPAPI加密算法的安全性. 因此, 使用DPAPI加密算法加密数据相当于使用了Windows、应用程序两个级别的数据保护^[4].

RSA数字签名算法的安全性高、理论性简单、易于实现, 是目前应用最为广泛的数字签名算法. 因其公钥和私钥的不同, 无法由其中一个密钥推断出另一个密钥^[11], 这是RSA算法的安全性所在. 目前攻击RSA数字签名算法的方法主要有算法攻击和存在性伪造攻击^[9]. 其中算法攻击的本质是指破解RSA的私钥, 也就是对大整数进行因式分解, 而大整数因式分解的安全性到目前为止还没有得到理论上的完全证明, 许多专家一致认为RSA算法的安全性等同于分解大整数的难度, 并且与RSA相关的变体算法也已经被证明相当于大数分解^[12], 所以为了防止该类攻击, 通常使用较长的模数长度; 而存在性攻击是指攻击者或通信双方之外的第三方仿冒数据的有效签名, 以此来谋取公钥和私钥, 从而达到破解数字签名的目的. 为了防止数字签名遭受以上攻击, RSA数字签名算法通常采用RSA填充技术进行抵抗, 该技术又称为概率签名标准技术. RSA填充技术是一种基于RSA密码体制的签名方案, 它可以很好的防范上述攻击, 在RSA数字签名算法中应用广泛^[9].

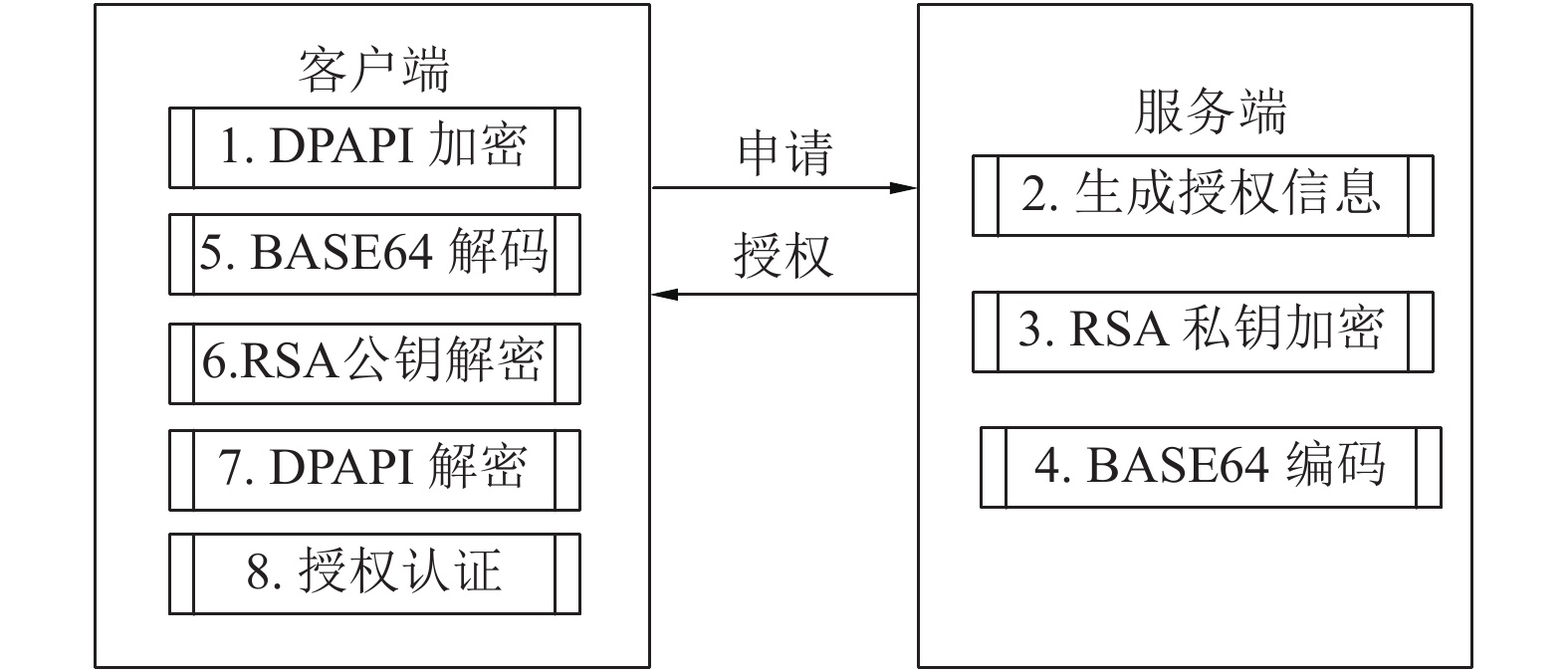
综上所述, DPAPI加密算法和RSA数字签名算法的安全性及保密性都有一定的保证. 若两种加密算法能够很好地结合, 就可以设计出一个DPAPI与RSA混合的加密算法, 既能保证数据接收方的正确性, 又可以保证数据发送方的信息不会被仿冒. 将该混合算法应用于软件的授权过程, 更好地保证授权安全, 是本文研究的目的所在. DPAPI与RSA混合加密算法的架构图如图3.

3.2 DPAPI与RSA混合加密算法的原理

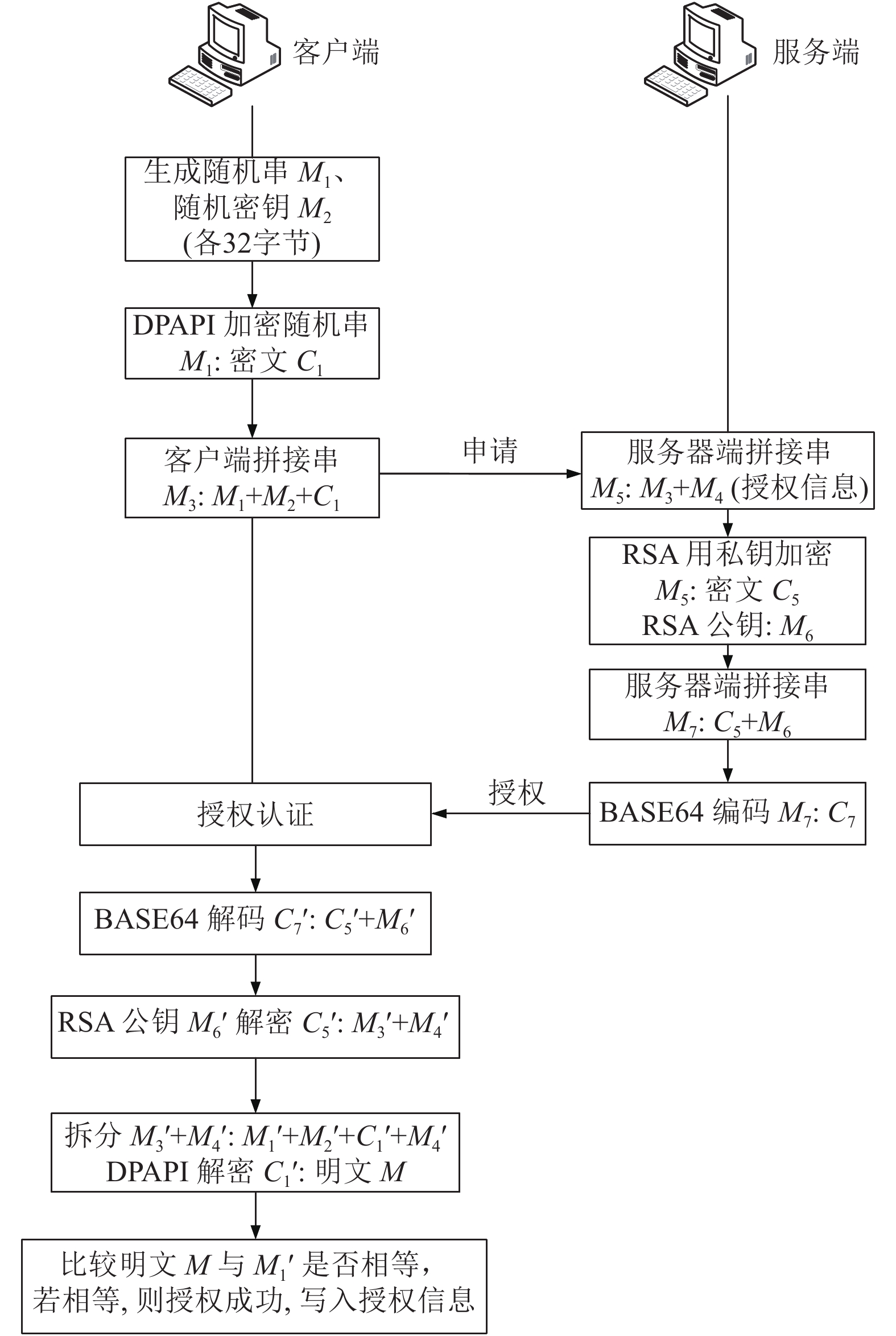
DPAPI加密算法一机一用的特点对于软件授权来说是判断是否正确授权的重要参考, 其次, 利用RSA数字签名算法的私钥对授权信息进行加密可以保证通信双方之外的第三方无法伪造该信息, 也是证明发送方信息真实性的依据^[13]. 本文将DPAPI加密算法与RSA数字签名算法进行混合并应用于软件授权上. DPAPI与RSA混合应用示意图如图4所示.

具体实现原理如下:

(1)客户端通过自定义函数随机生成随机串 ${M_1}$ 和随机密钥 ${M_{\rm{2}}}$ , 长度均为256位.

(2)客户端通过CryptProtectData()函数对随机串 ${M_1}$ 进行DPAPI加密得到密文 ${C_1}$ , 密文长度为402位.

(3)拼接随机串 ${M_1}$ 、随机密钥 ${M_{\rm{2}}}$ 、密文 ${C_1}$ , 得到客户端拼接串 ${M_{\rm{3}}}$ , 长度为256+256+402=914位.

(4)客户端将拼接串 ${M_{\rm{3}}}$ 发送给服务器, 服务器端在客户端拼接串 ${M_{\rm{3}}}$ 中加入授权信息 ${M_{\rm{4}}}$ , 此处的授权信息为软件使用截止日期, 如: 2088-08-08, 得到服务器端拼接串 ${M_{\rm{5}}}:{M_3} + {M_4}$ , 长度为914+10=924位.

(5)服务器端将拼接串 ${M_{\rm{5}}}$ 通过RSA私钥进行加密, 实验中RSA相关函数的使用来自OpenSSL软件库包. 其中服务器端使用RSA_private_encrypt()函数来对拼接串 ${M_{\rm{5}}}$ 进行私钥加密, 从而获得密文 ${C_{\rm{5}}}$ .

(6)服务器端将密文 ${C_{\rm{5}}}$ 与RSA公钥 ${M_{\rm{6}}}$ 拼接成字符串 ${M_{\rm{7}}}:{C_5} + {M_6}$ , 并通过BASE64编码得到字符串 ${C_{\rm{7}}}$ .

(7)服务器端发送授权文件(字符串 ${C_{\rm{7}}}$ )到客户端, 客户端接收并进行授权认证, 执行BASE64解码, 得到 ${C_{\rm{7}}}^\prime : {C_5}^\prime + {M_6}^\prime $ , 再由RSA公钥 ${M_6}^\prime $ 通过RSA_public_decrypt()函数对 ${C_{\rm{5}}}^\prime $ 进行解密得到服务器端拼接串 ${M_{\rm{5}}}^\prime :{M_{\rm{3}}}^\prime + {M_{\rm{4}}}^\prime $ .

(8)客户端拆分 ${M_{\rm{3}}}^\prime + {M_{\rm{4}}}^\prime $ 得到 ${M_{\rm{1}}}^\prime + {M_{\rm{2}}}^\prime + {C_1}^\prime + {M_4}^\prime $ , 由随机密钥 ${M_{\rm{2}}}^\prime $ 通过CryptUnprotectData()函数对密文 ${C_1}^\prime $ 进行解密得到明文随机串M. 比较随机串M和 ${M_{\rm{1}}}^\prime $ , 若相等, 写入授权信息 ${M_{\rm{4}}}^\prime $ , 否则授权失败.

4 DPAPI与RSA混合加密算法的实现

利用实验室工程应用中的软件对本文设计的混合加密算法进行验证(使用3台机器进行验证). 机器A和B分别作为客户端1和2来安装软件并利用客户端1进行软件授权的申请, 机器C作为服务器端用于返回授权文件. 如果在客户端1上进行了加密, 那么在客户端1上能够解密且在客户端2上解密失败, 则视为验证通过. 3台机器之间通过传送授权文件进行通信, 进而验证混合加密算法的正确性及可行性, 其中授权文件中包含用于比较验证的密文数据及授权信息.

由于DPAPI加密算法在Windows 2000及以上的操作系统中都有函数功能接口, 用户及操作系统程序都可以直接使用它. 例如在VC环境下, 引用头文件<Windows.h>和<wincrypt.h>, 就可以调用DPAPI的加密解密函数. 对于RSA相关函数, 该实验通过引用OpenSSL软件库包来提供. 搭建过程如下: 在Windows环境下安装和编译OpenSSL, 编译成功后再配置VC的OpenSSL开发环境, 即把OpenSSL库中include文件下的OpenSSL文件拷贝至VC安装目录下的include文件夹中, 再将lib文件夹下的库文件拷贝至VC的lib文件夹中, 最后, 在VC的项目工程里设置工程属性将库添加进去, 测试成功就可以使用RSA的相关函数了. 如图5所示, 客户端生成随机串和随机密钥.

根据图4可知, 混合加密算法主要有DPAPI加密、RSA私钥加密、BASE64编码、BASE64解码、RSA公钥解密、DPAPI解密操作6个步骤. 因此在实现DPAPI与RSA混合加密算法时, 要用到相应加密算法的函数, 具体有以下4个核心函数(由于参数较多此处省略介绍, 详情可查看官方文档):

1) DPAPI_IMP BOOL CryptProtectData();

2) int RSA_private_encrypt();

3) int RSA_public_decrypt();

4) DPAPI_IMP BOOL CryptUnprotectData().

函数1的作用是将参数pDataIn的实参值转换为DPAPI加密的密文, 即客户端提交的明文(随机串 ${M_1}$ )转换成DPAPI加密后的密文 ${C_1}$ . 同时设置参数dwFlags的取值为CRYPTPROTECT_LOCAL_MACHINE, 将加密的数据与当前计算机关联,而不是与单个用户关联. 关联后, 该加密数据只能在该机器上进行解密操作, 否则解密出的数据与原先的明文数据不同, 进而不能获得授权.

函数2的功能是对服务器端的拼接串 ${M_5}$ (图6)进行RSA私钥加密, 即进行数字签名. 服务器端先接收客户端发送的信息 ${M_3}$ 并通过字符串拼接函数将授权信息 ${M_4}$ 与 ${M_3}$ 进行拼接, 然后再进行RSA私钥加密. 本文通过调用PEM_write_bio_RSAPrivateKey()函数来生成私钥(图7), 再利用PEM_read_bio_RSAPrivateKey()函数将RSA私钥信息存储在参数rsa中. 在进行RSA私钥加密之前需将字符串进行分割, 因padding参数采用RSA_PKCS1_PADDING填充方式,采用该模式进行RSA加密对密文的长度存在限制,密文最大长度为117位.此处采用分段加密,将服务器端拼接串 ${M_5}$ 分成 $\left\lceil {924 \div 117} \right\rceil = 8$ 段,其中 $\left\lceil x \right\rceil $ 表示不小于 $x$ 的最小整数. 最后, 对RSA私钥加密后的信息再进行二次处理,通过Base64编码得到字符串 ${C_{\rm{7}}}$ , 增加了字符串的安全性.

客户端对字符串 ${C_{\rm{5}}}^\prime $ 进行RSA公钥解密操作即函数3的功能. 客户端接收授权文件( ${C_{\rm{7}}}$ )并进行授权认证, 利用Base64执行解码操作, 再利用RSA公钥对解码后的信息 ${C_{\rm{5}}}^\prime $ 进行解密操作(图8). 本文通过调用PEM_write_bio_RSAPublicKey()函数来生成公钥(如图9), 再利用PEM_read_bio_RSAPublicKey()函数将RSA公钥存储在函数3的参数rsa中, 且参数padding的取值与RSA私钥加密函数的padding参数相同, 也采用RSA_PKCS1_PADDING填充方式. 本文中对RSA公钥解密后的字符串再进行拆分操作,便于进行DPAPI解密操作.

客户端对字符串 ${C_1}^\prime $ 进行DPAPI解密操作即函数4的功能. 函数3执行过后, 客户端再利用字符串拆分函数对RSA公钥解密后的信息进行字符串拆分保存, 将拆分后的信息通过函数4进行解密, 解密后的信息再与拆分保存的字符串通过验证函数进行对比验证(如图10), 验证函数返回值为true时才可进行软件授权信息的写入.

基于上述对混合加密算法的验证可知, 相较于单独使用DPAPI或者RSA加密算法进行软件授权, 该混合加密算法的安全性是增大的, 且混合加密算法的两层加解密过程是分别调用官方库函数进行的, 不会过多的消耗计算资源, 还进一步增大了第三方破解该加密方案的复杂度. 其次, 因DPAPI和RSA加密算法本身具有较强的抗攻击特性, 理论上对于常见的攻击方式, 混合加密算法可做到很好的抵御. 最后, 本文提出的混合加密方案是在服务端加密和客户端加解密过程来完成一次软件授权的, 通过实验可知, 两层加密解密过程是有效的, 即该混合加密算法是可行的.

5 结束语

首先, 文章介绍了DPAPI加密算法和RSA数字签名算法的原理及安全性依据. 其次, 介绍了DPAPI与RSA 混合加密算法在软件授权过程中的应用原理. 最后, 在VC环境下实现并验证了这一混合算法. 该算法结合了二者的优点. DPAPI加密算法用于对客户端申请授权的信息进行加密, 在一机一用的前提下保证授权的正确性; 再用RSA算法的私钥加密服务器端的授权信息保证了授权信息不会被仿冒. 由此可见, DPAPI加密算法与RSA数字签名算法的混合, 能更好的保证软件在授权过程中的正确性和安全性, 同时, 该混合算法在实验室的工程应用中得到了验证, 表明该算法具有一定的可行性, 可以作为一种软件授权方案进行推广和使用.