2. 中国科学院 合肥物质科学研究院 等离子体物理研究所, 合肥 230031
2. Institute of Plasma Physics, Hefei Institutes of Physical Science, Chinese Academy of Sciences, Hefei 230031, China
托卡马克磁约束聚变装置是实现热核聚变最具有前景的手段. EAST (Experimental Advanced Super-conducting Tokamak) 核聚变装置是我国自主要发的全超导托卡马克[1]. 托卡马克装置放电时由于磁流体不稳定性、约束性能下降和储能快速损失会导致等离子体电流瞬间熄灭, 即破裂(disruption)[2-4]. 等离子体破裂会对装置造成严重损害, 限制可达到的运行参数. 目前EAST主要的破裂避免和缓解系统是大量气体注入(Massive Gas Injection, MGI)、散弹弹丸注入. EAST的MGI系统从响应到气体到达破裂区的时间大约10 ms[5]. 而破裂预测是破裂避免和缓解的前提, 因此对破裂进行预测尤为重要.
实验中已观察到多种破裂类型, 如锁模破裂、垂直位移破裂、密度极限破裂等. 等离子体密度是托卡马克装置3大运行极限之一[3], 高密度运行有利于达到聚变点火条件且是实现聚变的必要条件, 如国际热核聚变实验堆(ITER) 将以0.85
通常, 等离子体破裂分为3个阶段: 先兆阶段(1 ms~100 ms)、热猝灭阶段(~0.1 ms)、电流猝灭阶段(~10 ms), 这3个阶段的时间与装置尺寸有关, 且有的破裂没有先兆或先兆时间极短[6,11]. 此外, 破裂是一个非常复杂的非线性物理过程, 其物理机制复杂, 破裂原因、种类、先兆繁多, 这些原因通常不是单一而是相互耦合在一起的, 所以仅依靠先兆活动或者物理理论模型的研究远达不到预测的目的[12].
因此, 在各大装置上进行了数据驱动的机器学习模型进行预测的探索, Cannas等[13]在2004年利用MLP对JET装置进行破裂预测, 成功预测率达85%; 同样是Cannas等[14]利用自组织映射(SOM)对JET装置提取出破裂炮中属于非破裂阶段的样本, 再利用MLP进行训练; Ratta等[15]在2013年利用遗传算法对诊断信号进行特征提取; 文献[16,17]利用SVM对JET进行破裂预测, 成功预测率达82%; 马瑞等[18]利用MLP对HL-2A进行破裂预测, 但是使用的标签是0或者1, 不能很好地反映破裂发生的情况; Cannas等[19]利用SOM和MLP对ASDEX装置进行不区分种类的预测, 成功预测率为80%; 文献[20,21]利用随机森林对Alcator C-MOD、DIII-D以及EAST进行破裂预测的研究和对比, 对EAST的破裂炮成功预测率为91%; 以上破裂预测的研究都是不区分某种破裂类型的, 也就是只把放电炮分为破裂炮和非破裂炮, 而不区分破裂种类. 谭胜均等[22]利用双变量分析方法对EAST垂直位移不稳定破裂进行破裂预测的研究, 其中垂直位移破裂炮仅有2016年内72炮. Sengupta等[8]利用MLP对ADITY装置的密度极限值进行预测, 但训练集仅12炮放电. 王绅阳等[9]对J-TEXT装置用MLP进行密度极限值的预测, 在提前5 ms预测的前提下成功预测率为80%; 胡斐然等[10]利用MLP对J-TEXT进行密度极限破裂的预测, 受文献[13]启发, 使用的输出是在破裂前的固定时间内才开始上升的Sigmoid函数, 最终在至少提前30 ms触发预警的前提下成功预测率为90%, 错误预测率为10%. 但目前没有关于EAST密度极限破裂预测的研究.
基于以上, 本文首次对EAST密度极限破裂进行离线预测算法的研究, 离线算法是实时在线预测的前提. 除MLP, LSTM[23-26]也被用于预测器的构建, LSTM专用于时间序列数据的处理, 被广泛的应用于自然语言处理领域, 而EAST每次放电的数据是长时脉冲, 属于典型的时序数据.
文章组织如下: 第1节介绍密度极限破裂预测的意义以及目前的研究现状; 第2节简要的介绍密度极限破裂、数据库的建立; 第3节阐述诊断信号的选择和数据预处理; 第4节介绍模型的大致原理, 数据集的划分、模型输出以及评价指标; 第5节介绍相关结果; 第6节总结.
2 EAST密度极限破裂及数据库的建立 2.1 EAST密度极限破裂根据劳森判据, 为了达到聚变点火条件, 等离子体温度、密度以及能量约束时间的乘积需要达到一定值[3,6], 然而给定一个等离子体电流, 密度存在最大的安全运行值, 当超过这个密度上限后. 就会发生密度极限破裂.
密度极限破裂的物理机制尚不明确[6], 经过长期的实验研究与数据统计, 目前有多种计算密度极限的定标关系, 最广泛认同的是Greenwald定标律[6]:
| ${n_{{\rm{GW}}}}({10^{20}}{m^{ - 3}}) = \frac{{{I_{{P}}}({{MA}})}}{{{{{\text{π}} }}{a^2}({{{m}}^2})}}$ | (1) |
其中,
Zheng等[7]对EAST密度极限运行做了详尽研究. EAST通过持续的较强甚至正常充气就可能实现高密度极限放电. EAST的密度极限与Greenwald定标率吻合. 这为密度极限破裂数据库的筛选提供了重要的指导意义.
图1是典型的密度极限破裂炮, 1.7 s后电流进入平顶段, 而电子密度持续增加, 在7.2 s时开始出现不稳定性先兆, 密度达到0.8
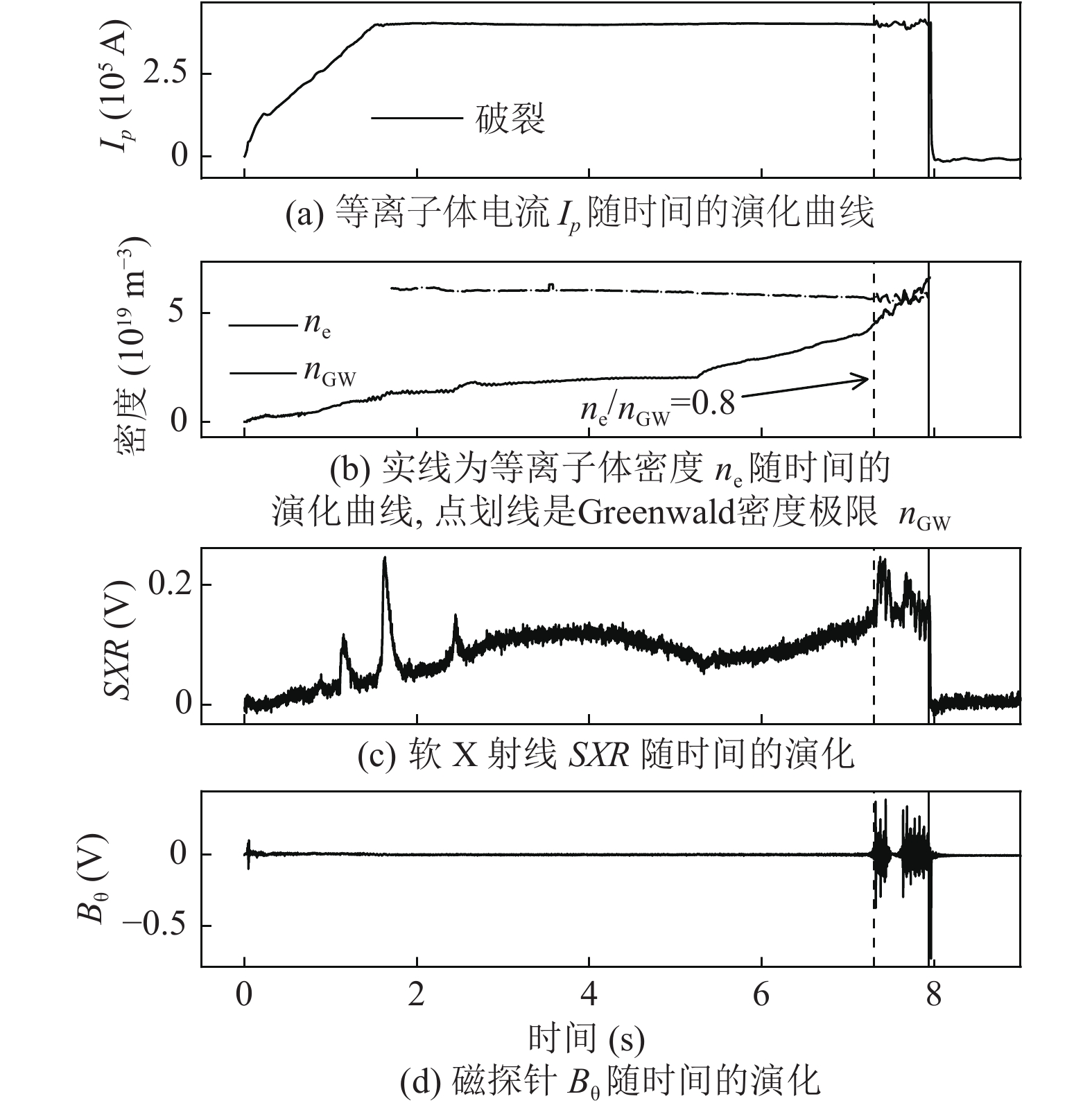
|
图 1 典型密度极限破裂炮(#67039) |
2.2 数据库的建立
本文根据Greenwald定标率建立EAST密度极限破裂数据库, 分为3步:
(1) 首先区分出破裂炮和非破裂炮. 这主要依赖于诊断信号
(2) 其次是从破裂炮中区分出密度极限破裂炮. 筛选标准是根据实际密度和Greenwald密度极限的比值
(3) 最后剔除缺失了对预测任务重要的诊断信号的放电炮.
根据以上3步, 设计自动筛选程序, 最终筛选出EAST聚变装置2014年到2019年、炮号分布在45000~88299之间的972炮平顶段破裂的密度极限破裂炮.
3 特征选择及数据预处理 3.1 特征选择EAST装置有上百种诊断信号, 选出最能表征破裂的诊断信号对于破裂预测任务至关重要, 一方面: 过多的信号会造成过大的计算量, 另一方面: 过少的诊断信号不能很好地表征破裂. 本文选取了电子密度(
由于这13种诊断信号的原始采样率不一致, 因此本文对原始信号进行插值重采样, 且重采样时间间隔为1 ms (破裂3个阶段的时间尺度).
此外, 不同诊断系统的诊断信号的数量级相差很大, 这巨大差异会导致神经网络权值的差异不是反映模型输入的相对重要性而是反映数量级的差异, 且会降低神经网络的训练速度, 因此还需对各信号做归一化:
| $x_{jN}^i = \frac{{x_j^i - {m_j}}}{{{M_j} - {m_j}}}$ | (2) |
其中,
人工神经网络(ANN)源自生物学上神经系统, 其最重要的功能是实现复杂的、多维度的非线性映射. 采用不同的数学模型就会得到不同的神经网络方法. 其中最为经典的是MLP[8-10,13], 一般由输入层、隐藏层、输出层组成, 它的输入是一个个样本点, 且认为每个样本点是独立的.
循环神经网络(RNN)是用来处理序列数据的神经网络, 它克服了传统MLP对序列数据处理的低效, RNN相当于多个MLP横向连接, 相邻MLP之间的隐藏层之间全连接, 使得信息不仅可以向下一层传递信号, 而且可以向相邻MLP传递信号[23,24]. 作为一种特殊的循环神经网络, LSTM通过输入门、输出门、遗忘门不仅克服了RNN梯度消失和爆炸的问题, 而且还可以保持网络的长期记忆状态, 其误差反向传播由通过时间的反向传播算法(BTPP)来解决. LSTM有多种形式, 考虑到计算量以及输入输出在时间上的相关性, 本文采用many-to-many形式, 其具体结构如图2所示.
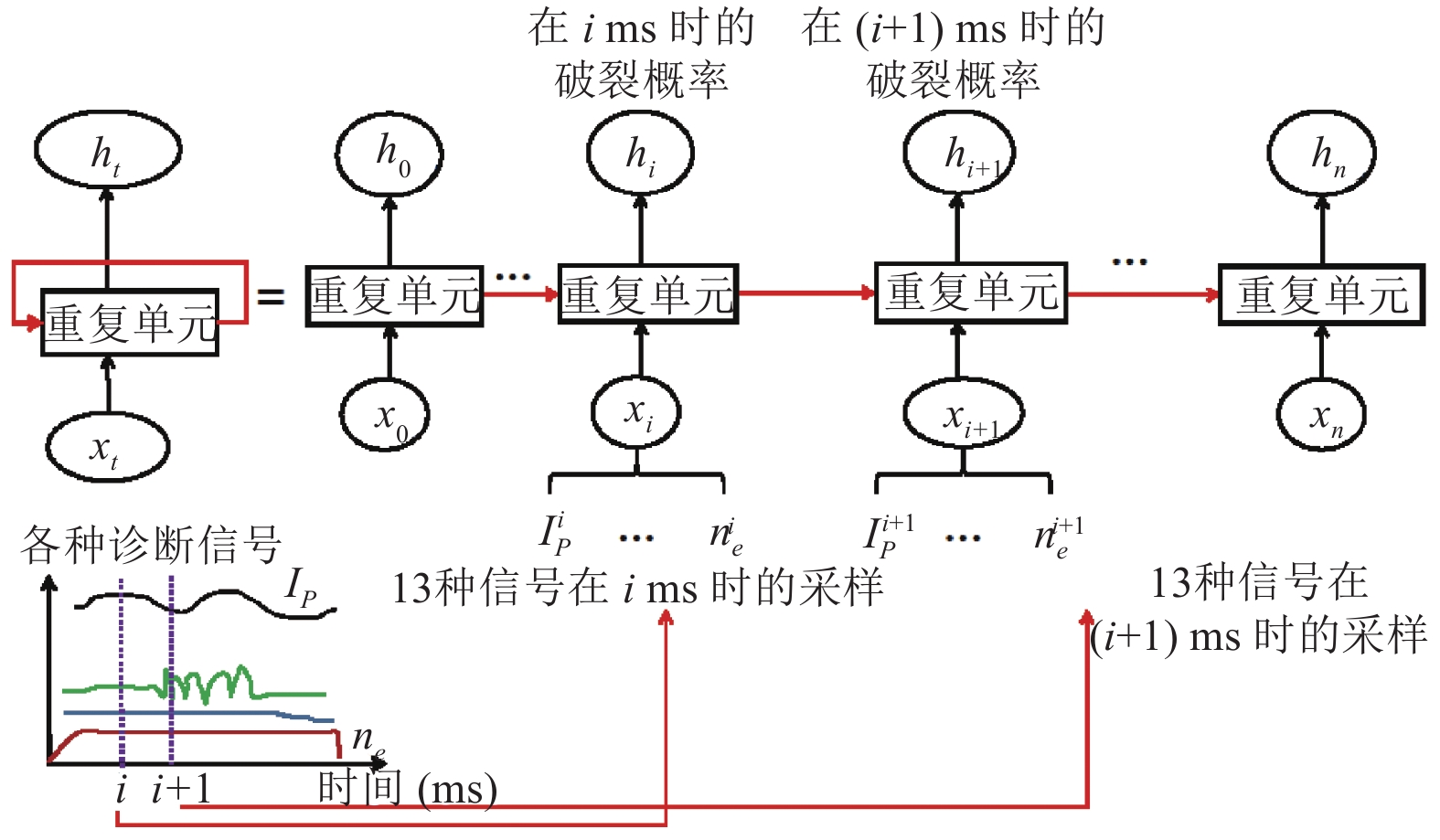
|
图 2 LSTM结构图 |
LeakRelu激活函数[26]相比于其他激活函数具有收敛速度快、解决梯度消失问题、缓解过拟合等优点因而近年来受到广泛的关注, 本文的隐藏层采用LeakRelu激活函数, 输出层采用Sigmoid函数, 优化算法为Nadam[26].
本文中LSTM的时间步选为100, LSTM和MLP的输入层和输出层神经元个数分别为13、1, 而隐藏层层数和每层神经元个数通过经过网格搜索[26]的方法试验了30个模型, 发现网络结构(13:200:200:1) 的结构相对较好, 为了便于比较, 因此MLP和LSTM都采用这一结构.
图2中的重复单元的数学原理如下:
| $\left\{ \begin{array}{l} {{{f}}_{{t}}} = \sigma ({W_f} \cdot [{{{h}}_{t - 1}},{{{x}}_t}] + {{{b}}_{{f}}})\\ {{{i}}_{{t}}} = \sigma ({W_i} \cdot [{{{h}}_{t - 1}},{{{x}}_t}] + {{{b}}_{{i}}})\\ {{{{\tilde c}}}_{{t}}} = {\rm tanh}({W_c} \cdot [{{{h}}_{t - 1}},{{{x}}_t}] + {{{b}}_{{c}}})\\ {{{c}}_{{t}}} = {{{f}}_{{t}}} \circ {{{c}}_{t - 1}} + {{{i}}_t} \circ {{{{\tilde c}}}_{{t}}}\\ {{{o}}_{{t}}} = \sigma ({W_o} \cdot [{{{h}}_{{{t}} - 1}},{{{x}}_t}] + {{{b}}_{{o}}})\\ {{{h}}_{{t}}} = {{{o}}_{{t}}} \circ {\rm tanh}({{{c}}_{{t}}}) \end{array} \right.$ | (3) |
其中,
本文训练集包括密度极限破裂炮和非破裂炮, 在每个时刻, 神经网络的输入为一个具有13个特征的样本. 数据集的划分如表1所示.
| 表 1 数据集的划分 |
模型训练时, 对于每炮密度极限破裂炮, 本文选取时间窗口[
(1) 对于密度极限破裂炮, 文献[10,13]中使用的输出是在破裂前的固定时刻才开始上升的Sigmoid, 本文使用的Sigmoid开始上升时刻并不是在破裂前的固定时间而是取决于实际密度达到0.5倍Greenwald密度极限的时刻, 如图3所示.
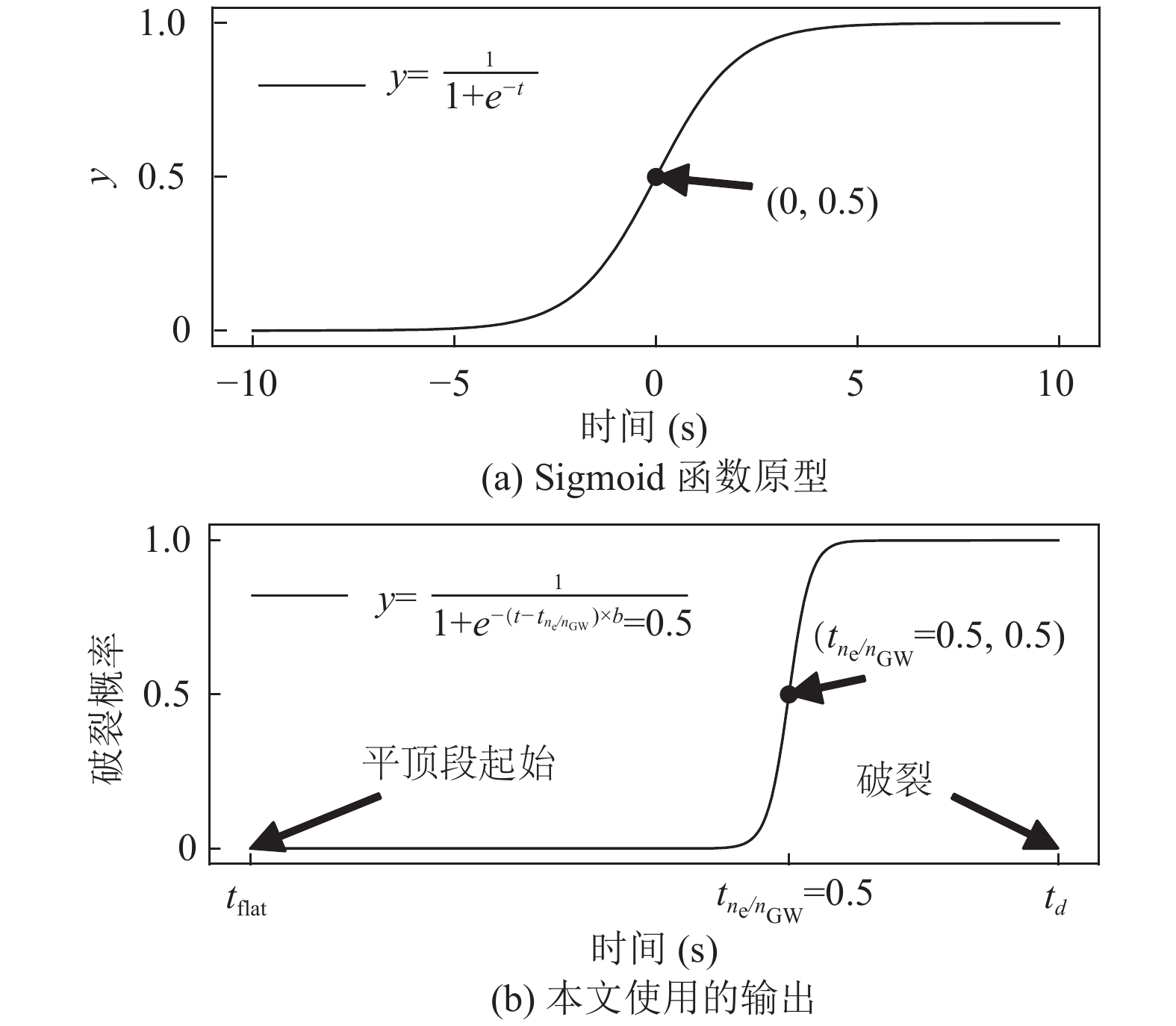
|
图 3 训练神经网络时密度极限破裂炮的输出 |
| $y(t) = \frac{1}{{1 + {e^{ - (t - {t_{{n_e}/{n_{{\rm{GW}} = 0.5}}}}) \times b}}}}$ | (4) |
其中,
(2) 对于非破裂炮, 训练时的输出恒为0, 即认为破裂的概率为0.
预测器的最终目的是能对即将发生破裂的放电炮在破裂前发出预警, 本质上是一个时序样本的分类问题, 但神经网络在实际使用时对于每炮放电的输出都是一个取值范围为0到1之间的时间序列, 因此在使用模型时需要选取一个阈值(
对于每炮放电脉冲, 预测结果可以分为以下:
(1)若为密度极限破裂炮(正例):
① 成功预测(successful alarm): 预测器至少在破裂发生前
② 遗漏预测(missed alarm): 在破裂前
(2)若为非破裂炮(反例):
错误预测(false alarm): 如果模型在任意时刻触发预警, 则此非破裂炮被判定为密度极限破裂炮, 因此为错误预警. 也称为“假正例(False Positive)”.
将密度极限破裂炮总数记为
(1) 成功预测率(
(2) 遗漏预测率(
(3) 错误预测率(
(4) 平均预警时间(
本文采用ROC (Receiver Operation Characteristic)曲线面积, 即AUC (Area Under ROC Curve)值作为阈值的选择标准, AUC值越大说明模型的分类性能越好[23,26]. ROC曲线的横轴为假正例率
| $t{h^*} = \mathop {\arg\max }\limits_{0 \le th \le 1} {{AUC}}(th,\Delta {t_{{\rm{alarm}}}})$ | (5) |
| 表 2 混淆矩阵 |
4.3 诊断信号敏感度的分析
本文采取“留一法”对诊断信号的敏感度进行分析, 具体如下: 每次移除一种诊断信号, 将剩余的12种诊断信号作为特征输入模型并在相同的训练集上进行训练, 接着在相同的测试集上进行测试. 同时, 计算模型实际输出和理论输出间的均方误差, 误差越大, 说明破裂预测对此诊断越敏感越, 即此诊断信号越重要. 最终的计算结果如图4, 可以看出, 等离子体电流(
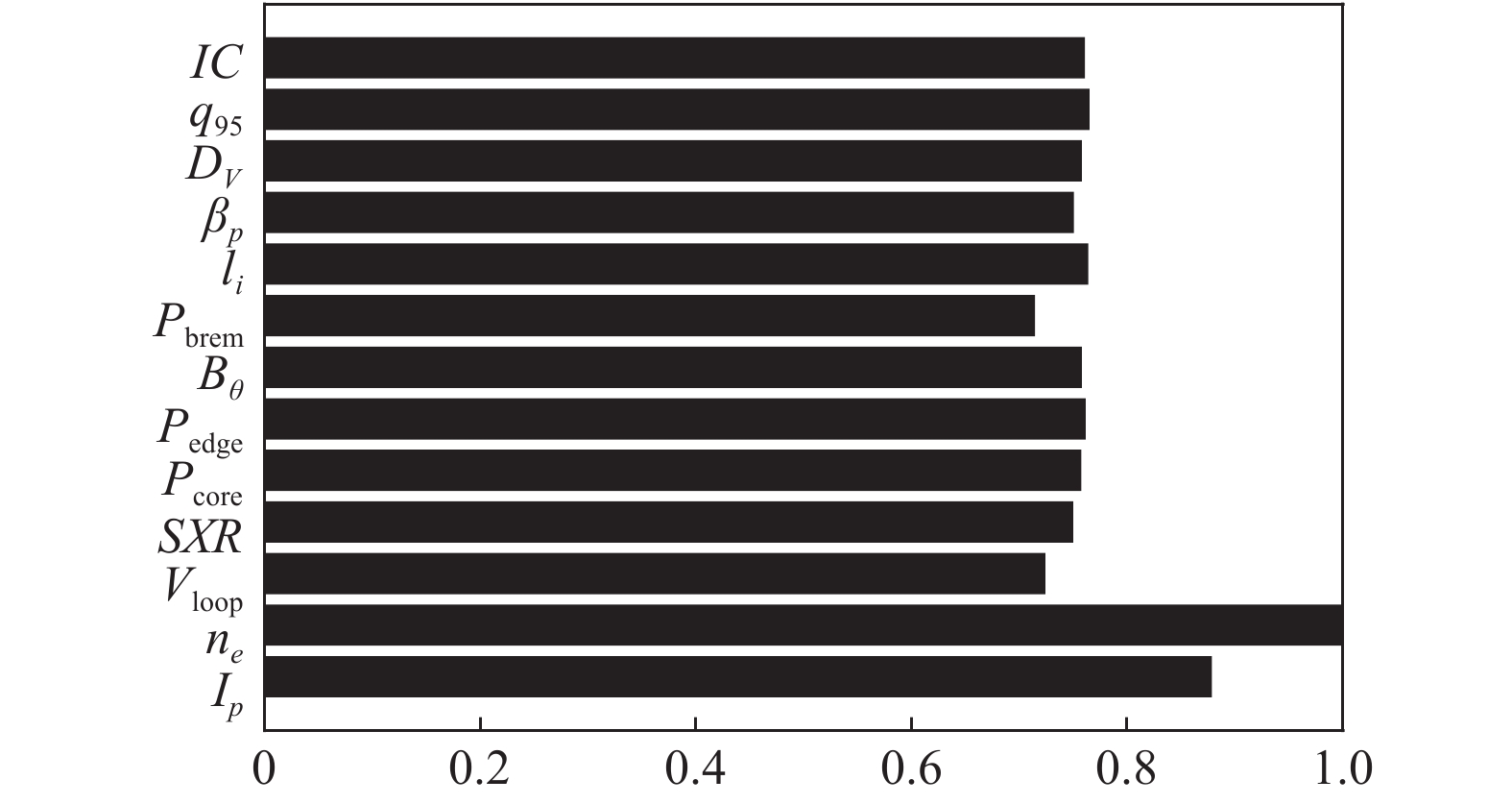
|
图 4 留一法对诊断信号的敏感度分析结果 |
5 实验与结果分析 5.1 收敛性及运算实时性
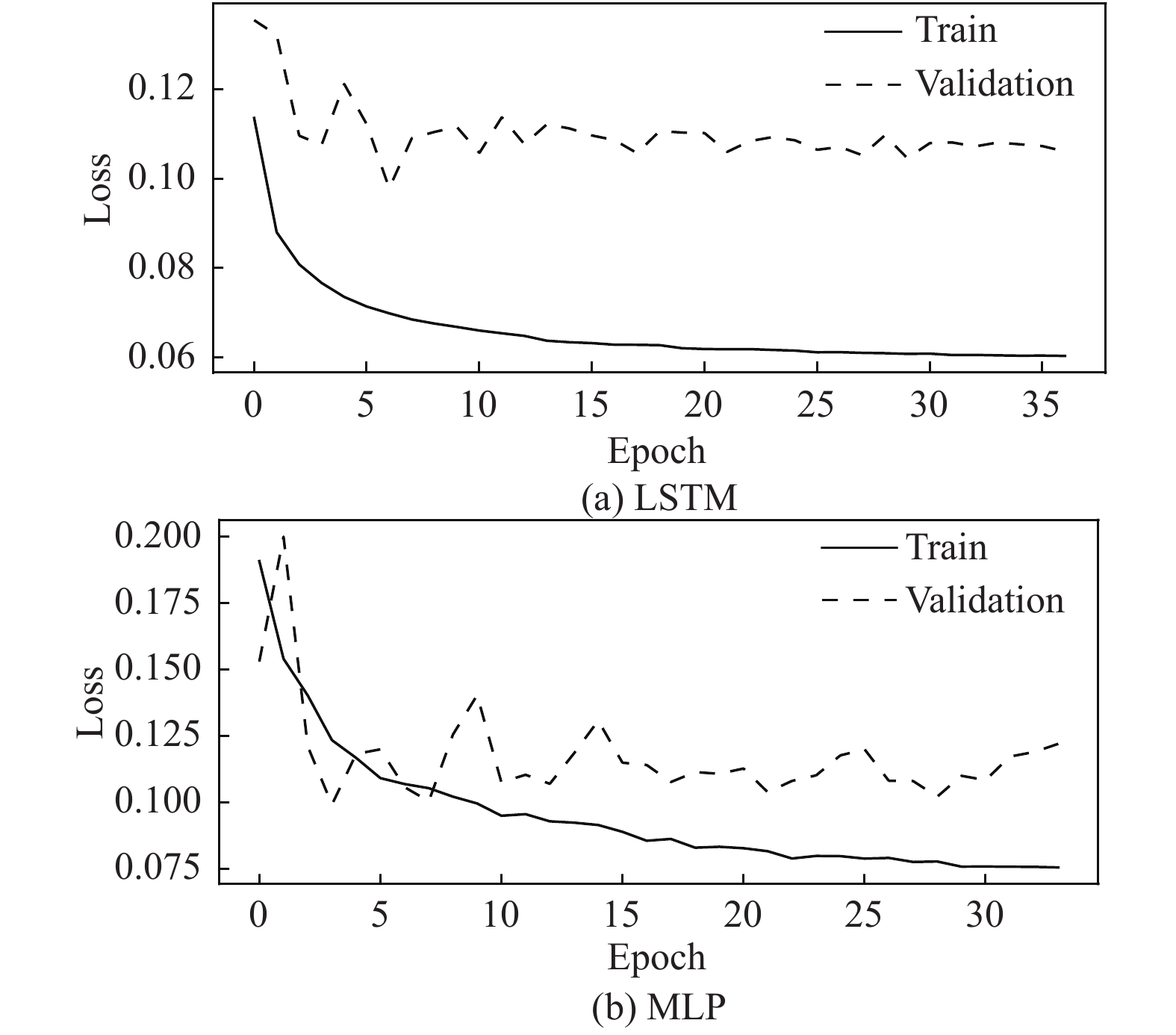
图5是模型训练过程中模型损失的变化, LSTM和MLP在训练集上的损失均是逐渐减小然后趋于稳定, 在验证集上损失整体也是呈现逐渐减小直至在一定范围内波动, 且LSTM的损失波动较小.
至于实时性, 在测试过程中, LSTM和MLP预测每个输入样本所需时间分别为0.000654 ms、0.010815 ms, 均小于样本之间的间隔时间(1 ms), 且测试过程中使用的是Python程序, 实际部署时会将模型转换为C语言, 运算速度更快, 更易满足实时预测需求.
|
图 5 实验过程中LSTM和MLP的损失变化 |
5.2 结果与性能分析
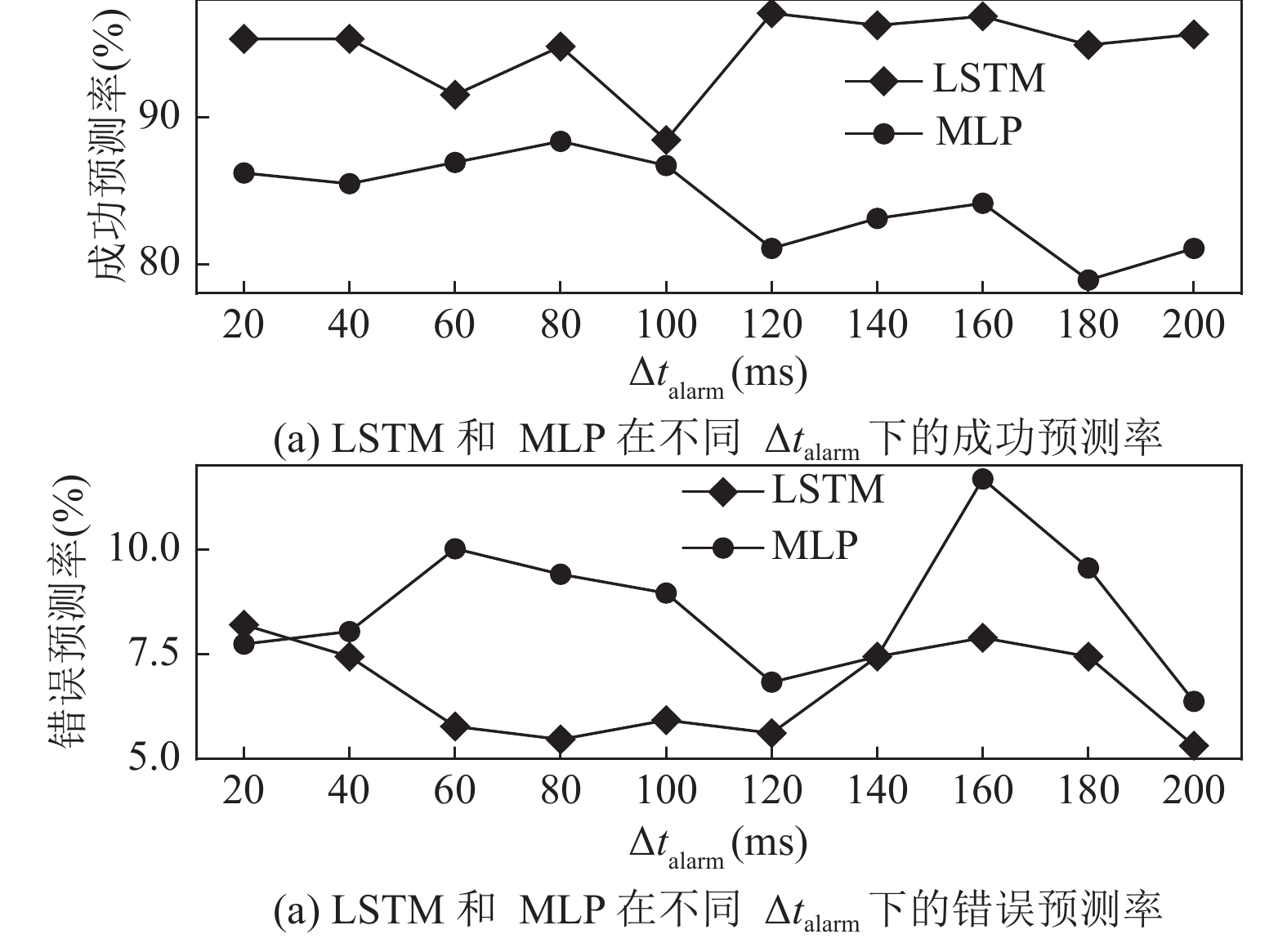
为了全面衡量模型的性能, 本文将
|
图 6 成功和错误预测率比较 |
接下来令
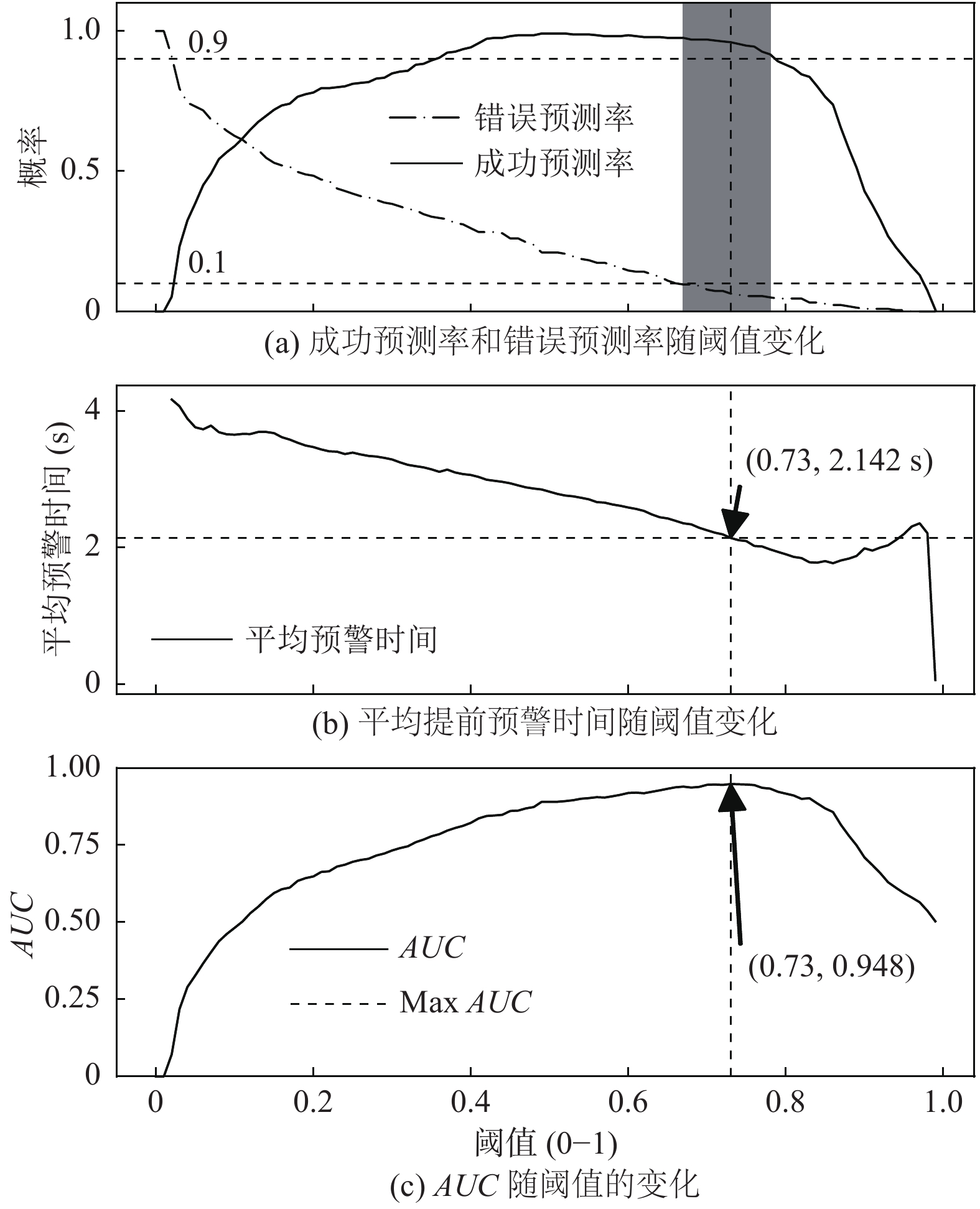
|
图 7 |
MLP和LSTM总体预测结果如表3所示. 从中可以看出, LSTM和MLP在所有数据上对密度极限破裂炮的正确预测率分别为95.37%和86.21%, 对于非破裂炮的错误预测率分别为8.21%和7.75%.
|
表 3 |
图8展示的是#66972炮密度极限破裂炮的预测结果. 可以看出, 该炮在
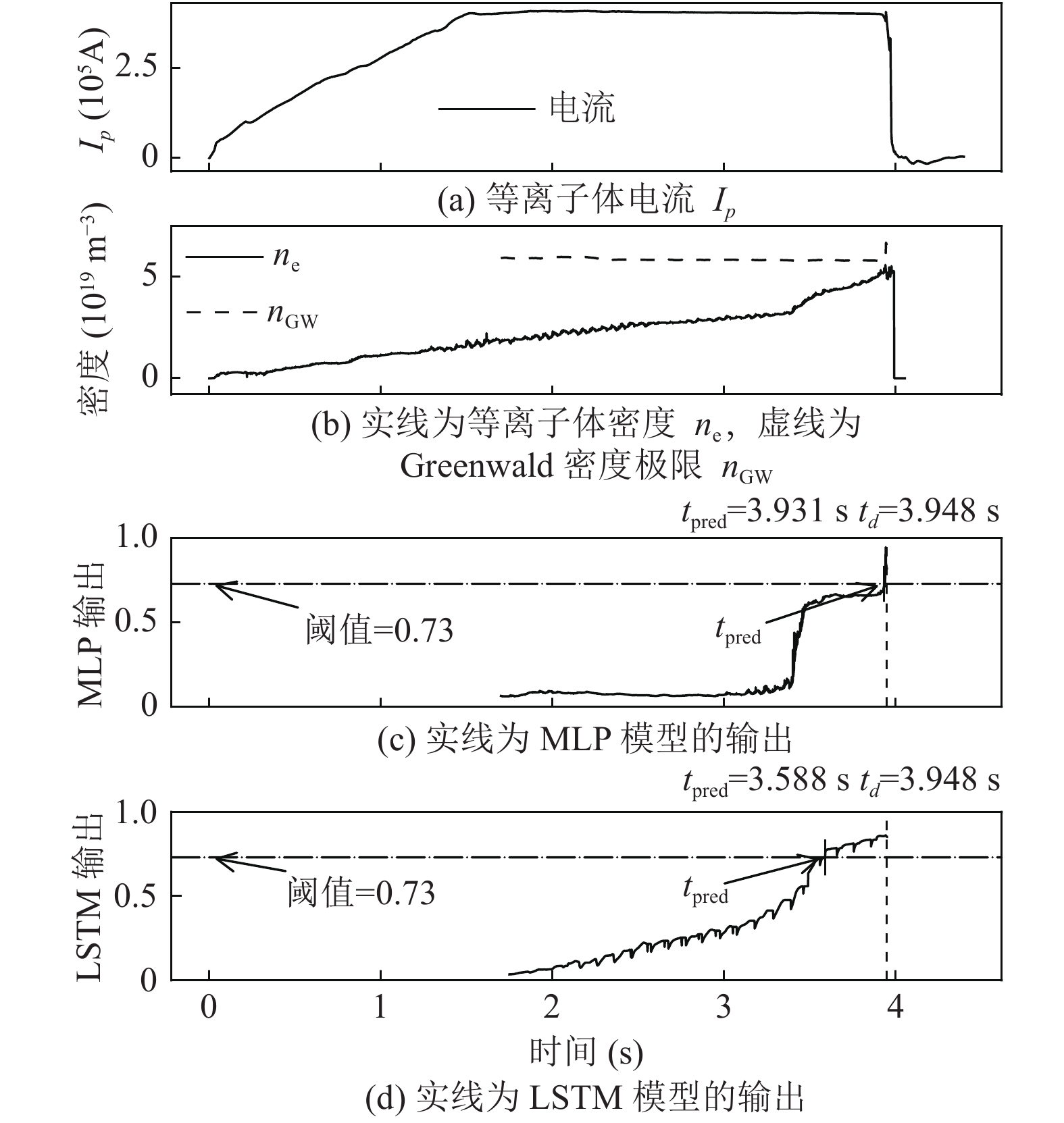
|
图 8 #66972炮密度极限破裂炮的预测结果 |
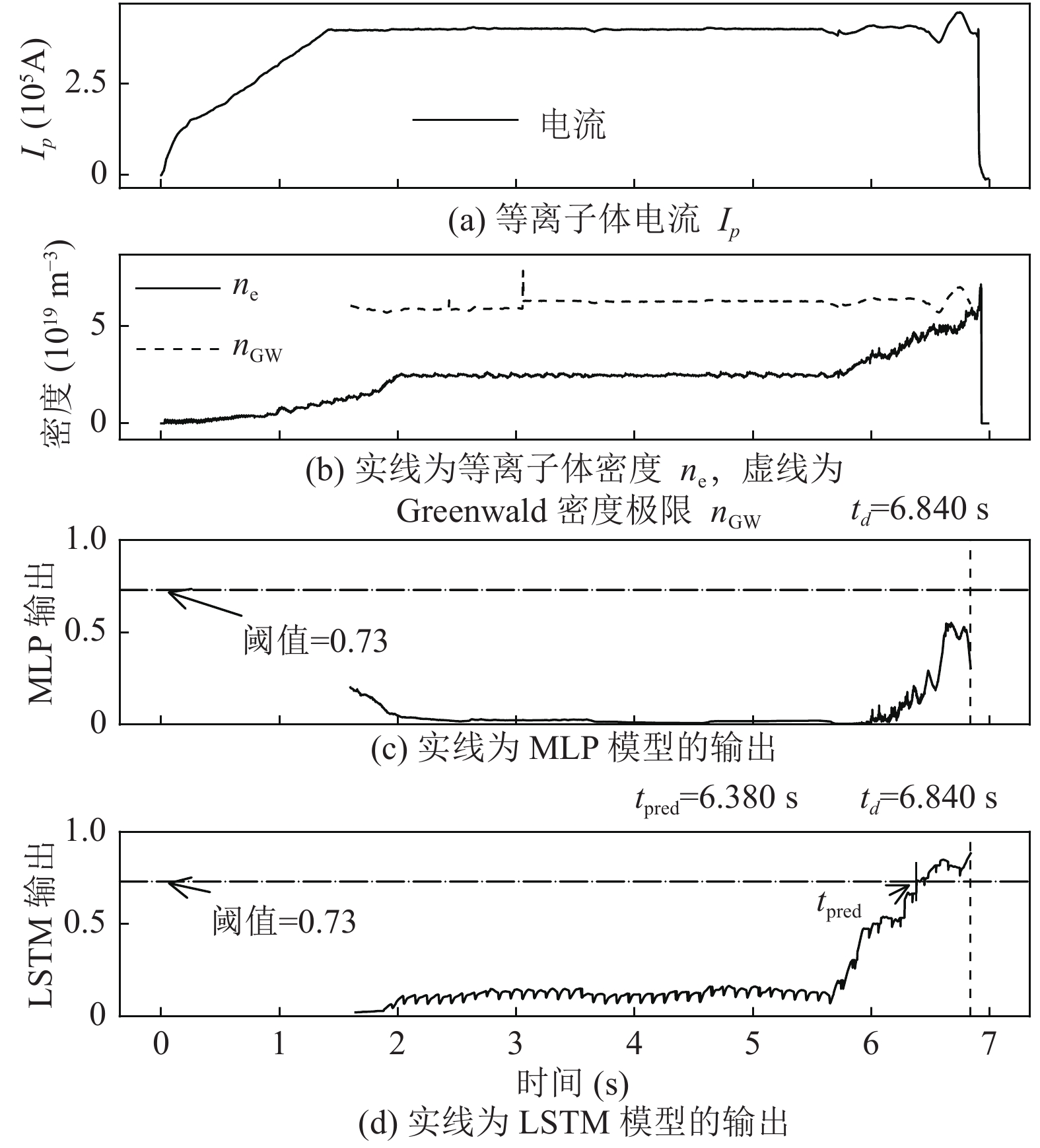
图9展示的是#69104炮密度极限破裂炮的预测结果. 可以看出, 该炮在
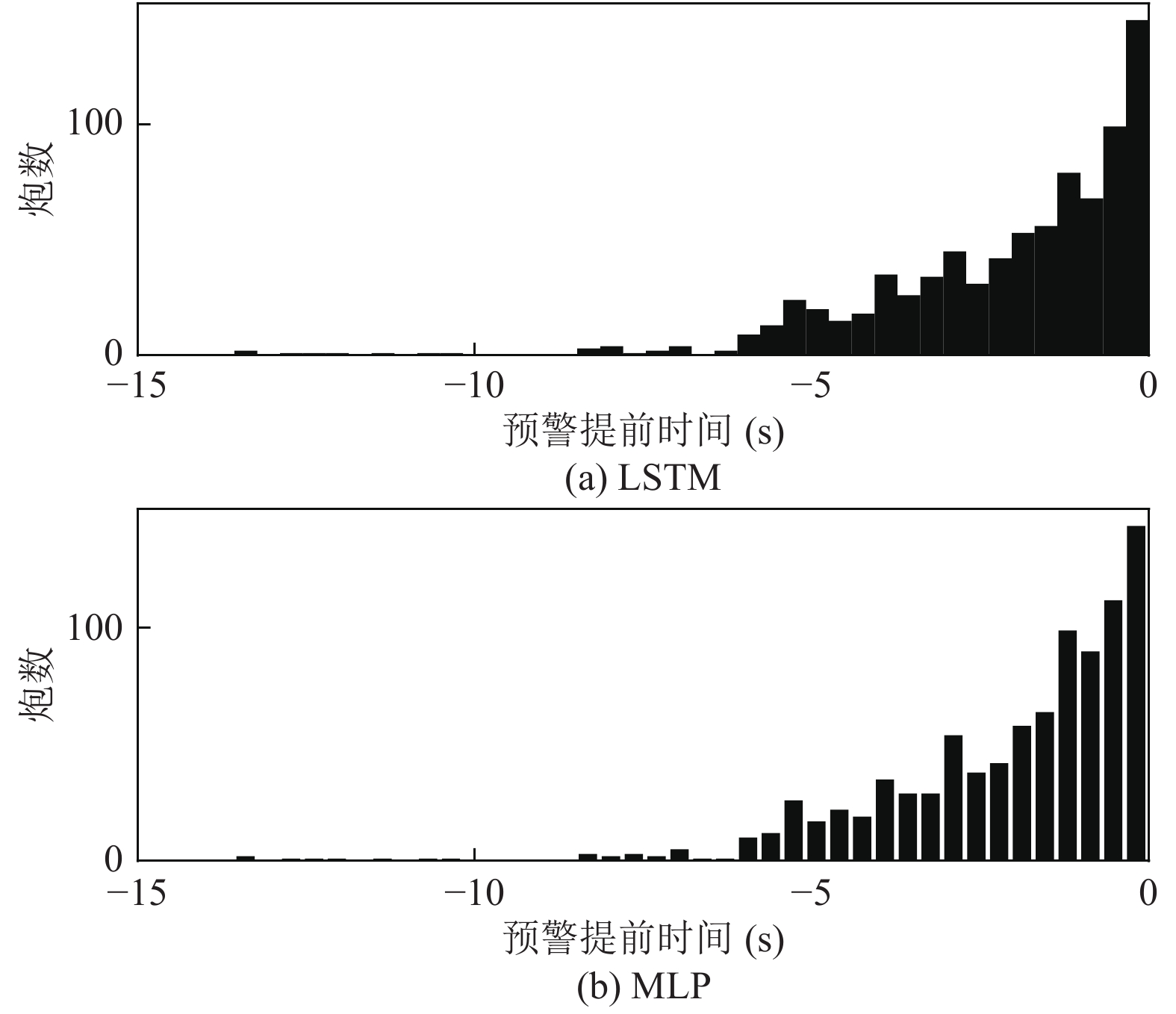
图10展示的是被LSTM和MLP成功预测的密度极限破裂炮的提前预警时间(
高密度运行对于未来的装置具有重要意义, 本文首次针对EAST采用神经网络进行密度极限破裂预测研究. 首先建立了EAST密度极限破裂数据库, 其次将MLP和LSTM分别建立离线模型, 模型输出为更具实际意义的考虑了实际密度和Greenwald密度极限相对大小的Sigmoid函数, 最后离线测试结果表明, 对于密度极限破裂炮, 在至少提前20 ms触发预警的前提下, LSTM和MLP对密度极限破裂炮的成功预测率分别为95.37%和86.21%, 对于非破裂炮的错误预测率分别为8.21%和7.75%. 本研究说明利用神经网络建立密度极限破裂离线预测算法的可行性, 下一步研究计划是在EAST托卡马克上实现破裂预警的实时在线计算.
|
图 9 #69104炮密度极限破裂炮的预测结果 |
|
图 10 被LSTM和MLP正确预测的密度极限破裂炮的预警提前时间(
|
| [1] |
柴文婷, 肖炳甲, 袁旗平, 等. EAST破裂炮的判定与波形显示. 计算机系统应用, 2018, 27(5): 156-160. DOI:10.15888/j.cnki.csa.006333 |
| [2] |
Schuller FC. Disruptions in tokamaks. Plasma Physics and Controlled Fusion, 1995, 37(11A): A135-A162. DOI:10.1088/0741-3335/37/11A/009 |
| [3] |
Hender TC, Wesley JC, Bialek J, et al. MHD stability, operational limits and disruptions. Nuclear Fusion, 2007, 47(6): S128-S202. DOI:10.1088/0029-5515/47/6/S03 |
| [4] |
Campbell D. 6 Magnetic confinement fusion: Tokamak. In: Heinloth K, ed. Nuclear Energy. Berlin: Springer, 2005.
|
| [5] |
Chen DL, Shen B, Granetz RS, et al. Disruption mitigation with high-pressure helium gas injection on EAST tokamak. Nuclear Fusion, 2018, 58(3): 036003. DOI:10.1088/1741-4326/aaa139 |
| [6] |
Greenwald M. Density limits in Toroidal plasmas. Plasma Physics and Controlled Fusion, 2002, 44(8): R27-R53. DOI:10.1088/0741-3335/44/8/201 |
| [7] |
Zheng XW, Li JG, Hu JS, et al. Density limits investigation and high density operation in EAST tokamak. Plasma Physics and Controlled Fusion, 2016, 58(5): 055013. DOI:10.1088/0741-3335/58/5/055013 |
| [8] |
Sengupta A, Ranjan P. Prediction of density limit disruption boundaries from diagnostic signals using neural networks. Nuclear Fusion, 2002, 41(5): 487. DOI:10.1088/0029-5515/41/5/302 |
| [9] |
Wang SY, Chen ZY, Huang DW, et al. Prediction of density limit disruptions on the J-TEXT tokamak. Plasma Physics and Controlled Fusion, 2016, 58(5): 055014. DOI:10.1088/0741-3335/58/5/055014 |
| [10] |
Zheng W, Hu FR, Zhang M, et al. Hybrid neural network for density limit disruption prediction and avoidance on J-TEXT tokamak. Nuclear Fusion, 2018, 58(5): 056016. DOI:10.1088/1741-4326/aaad17 |
| [11] |
ITER Physics Basis Editors. ITER physics expert group chairs and co-chairs and ITER joint central team and physics integration unit. Nuclear Fusion, 1999, 39(12): 2137-2174. DOI:10.1088/0029-5515/39/12/301 |
| [12] |
Cannas B, Fanni A, Murari A, et al. Automatic disruption classification based on manifold learning for real-time applications on JET. Nuclear Fusion, 2013, 53(9): 093023. DOI:10.1088/0029-5515/53/9/093023 |
| [13] |
Cannas B, Fanni A, Marongiu E, et al. Disruption forecasting at JET using neural networks. Nuclear Fusion, 2004, 44(1): 68-76. DOI:10.1088/0029-5515/44/1/008 |
| [14] |
Cannas B, Fanni A, Sonato P, et al. A prediction tool for real-time application in the disruption protection system at JET. Nuclear Fusion, 2007, 47(11): 1559-1569. DOI:10.1088/0029-5515/47/11/018 |
| [15] |
Rattá GA, Vega J, Murari A. Improved feature selection based on genetic algorithms for real time disruption prediction on JET. Fusion Engineering and Design, 2012, 87(9): 1670-1678. DOI:10.1016/j.fusengdes.2012.07.002 |
| [16] |
Rattá GA, Vega J, Murari A, et al. An advanced disruption predictor for JET tested in a simulated real-time environment. Nuclear Fusion, 2010, 50(2): 025005. DOI:10.1088/0029-5515/50/2/025005 |
| [17] |
Vega J, Dormido-Canto S, López JM, et al. Results of the JET real-time disruption predictor in the ITER-like wall campaigns. Fusion Engineering and Design, 2013, 88(6–8): 1228-1231. DOI:10.1016/j.fusengdes.2013.03.003 |
| [18] |
马瑞, 王爱科, 王灏. 用人工神经网络预测HL-2A等离子体放电破裂. 核聚变与等离子体物理, 2010, 30(1): 37-41. DOI:10.16568/j.0254-6086.2010.01.003 |
| [19] |
Cannas B, Fanni A, Pautasso G, et al. An adaptive real-time disruption predictor for ASDEX upgrade. Nuclear Fusion, 2010, 50(7): 075004. DOI:10.1088/0029-5515/50/7/075004 |
| [20] |
Rea C, Granetz RS, Montes K, et al. Disruption prediction investigations using machine learning tools on DIII-D and Alcator C-Mod. Plasma Physics and Controlled Fusion, 2018, 60(8): 084004. DOI:10.1088/1361-6587/aac7fe |
| [21] |
Montes KJ, Rea C, Granetz RS, et al. Machine learning for disruption warnings on Alcator C-Mod, DIII-D, and EAST. Nuclear Fusion, 2019, 59(9): 096015. DOI:10.1088/1741-4326/ab1df4 |
| [22] |
谭胜均, 张洋, 叶民友, 等. EAST上由垂直不稳定性引发破裂的分析与预测. 核聚变与等离子体物理, 2019, 39(2): 104-111. DOI:10.16568/j.0254-6086.201902002 |
| [23] |
LeCun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [24] |
Graves A. Long short-term memory. In: Graves A, ed. Supervised Sequence Labelling with Recurrent Neural Networks. Berlin: Springer, 2012. 37–45.
|
| [25] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [26] |
Goodfellow I, Bengio Y, Courville A. Deep Learning. Cambridge: The MIT Press, 2016.
|
| [27] |
唐剑寅, 肖炳甲, 袁旗平. 对EAST PCS系统延迟的分析与改善. 计算机系统应用, 2018, 27(11): 115-119. DOI:10.15888/j.cnki.csa.006606 |
| [28] |
De Vries PC, Pautasso G, Humphreys D, et al. Requirements for triggering the ITER disruption mitigation system. Fusion Science and Technology, 2016, 69(2): 471-484. DOI:10.13182/FST15-176 |
 2020, Vol. 29
2020, Vol. 29


