2. 国网山东省电力公司经济技术研究院, 济南 250001;
3. 国网山东省电力公司, 济南 250000
2. Economic & Technology Research Institute, State Grid Shandong Electric Power Company, Jinan 250001, China;
3. State Grid Shandong Electric Power Company, Jinan 250000, China
在能源与电力系统领域, 电力大数据具有数据规模大、数据类型多等多个特征, 因此, 对数据进行采集存储分析也比较困难[1]. 大数据挖掘分析及应用的关键要素是保障数据的真实性. 各类网络安全设备的日志信息反映的是用户对网络及业务系统的访问情况, 通过对各类安全日志信息进行深度挖掘, 能够分析出网络中的恶意攻击, 能够对公司安全隐患及时进行隐患消缺.
电力公司各单位为了确保公司网络安全稳定运行, 通过在网络出入口处部署入侵检测系统、入侵防御系统、防火墙等安全防护设备, 从而更好地保障公司内部网络安全性. 在设备运行过程中, 若有网络访问或攻击等行为, 设备都会通过安全日志记录下来, 从而达到实时监控网络攻击的效果. 由于各类网络安全设备功能有相似的地方, 因此不同设备产生的安全日志会存在较高的重复率, 网络管理人员很难找出日志隐藏的关联性, 从而对网络态势进行融合分析就相对比较困难[2]. 但是, IDS、IPS和防火墙等设备日志间缺乏协同机制, 其语义级别低, 设备日志信息结构多种形式并且数据分散在不同系统, 包含的安全日志信息相互隔离, 形成信息孤岛, 管理人员不能及时发现网络攻击并快速响应. 因此, 需要有一种方法来从各类日志信息中提取综合特征, 从而帮助管理人员从总体上把握信息系统的安全态势. 例如, 基于这些特征可以在宏观层面进行未知威胁检测等工作.
目前, 在网络设备日志融合方面主要有基于逻辑关系的算法和基于规则推理的算法等[2-4]. 基于逻辑关系的算法核心思想是通过采用常规经验来设计逻辑规则, 进而对日志信息内在的逻辑关系进行融合处理[3]. 基于规则推理的算法核心思想是通过量化评估多源日志信息的不确定性, 进而利用基于规则推理的思想去预测威胁[3]. 这些算法都需要一定程度的先验知识和领域专家知识. 在面向大量异构设备和不断演化的网络环境时, 适配性问题较为突出.
酆勇等[5]提出了一种基于受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)来表达输入语音超向量的说话人信息. 陈龙等[6]提出了一种融合多源日志的基于事件“前提/结果”因果关系的事件场景关联方法. 江雨燕等[7]提出了基于RBM的分布式主题特征提取模型可以更好地使用文档中的多标记信息. 程乐峰等[8]总结了深度学习、对抗学习和集成学习等7种代表性机器学习在电力系统调度优化和控制决策等方面的应用.
人工神经网络具有较强的非线性映射能力, 特别是受限玻尔兹曼机(RBM)神经网络具有较强的自编码能力[9-17]. 前期有学者对文本特征提取[18-20]进行了相关研究. 本文提出了基于受限玻尔兹曼机的多源日志信息综合特征提取方法, 采用受限玻尔兹曼机神经网络对各类日志信息进行融合处理, 有效解决了日志数据的异构性等问题, 提升了电力信息系统安全态势预测速度和精度.
2 基于RBM的多源日志综合特征提取方法 2.1 电力信息系统数据采集预处理电力信息系统数据采集预处理, 通过采集电力信息系统中各个设备包含的历史数据和实时数据的日志信息, 日志信息中包括设备状态信息、动态传输数据信息、安全防护信息及故障信息.
首先获取电力信息系统中各类设备, 例如安全设备、网络设备、主机及其他安全防护系统产生的日志信息, 并对采集到的原始数据进行实时的预处理和分析, 对原始数据的预处理包括数据去重、数据噪声去除等. 数据去重是确保所采集的数据是可信数据, 将源数据中的无关数据和噪声数据去除. 经过预处理的数据进行分布式存储, 对所有存储的数据创建数据索引, 以便后续查询追溯使用.
2.2 多源日志综合特征提取方法的思想对于每类日志信息r, 构建初始化受限波尔兹曼机神经网络RBMr, 其中r为1与t之间的正整数; t为日志信息的类数, 记为{ 日志1, 日志2, ···, 日志t }, 其数据维度分别为{M1, M2, ···, Mt}. 其中, 日志信息的类别是按照设备划分的, 不同的设备是不同的类别; 维度表示日志数据的字段数.
如图1所示, 初始化受限波尔兹曼机神经网络RBMr为具有可见层和隐藏层的两层网络, 将不同长度的日志信息数据输入后将其编码为长度为N的数据并输出, 可见层节点数与输入数据的维度相对应为Mr个, 隐藏层节点数为N个, 随机产生[0,1]之间的随机数作为RBM可见层节点和隐藏层节点之间的连接权值.
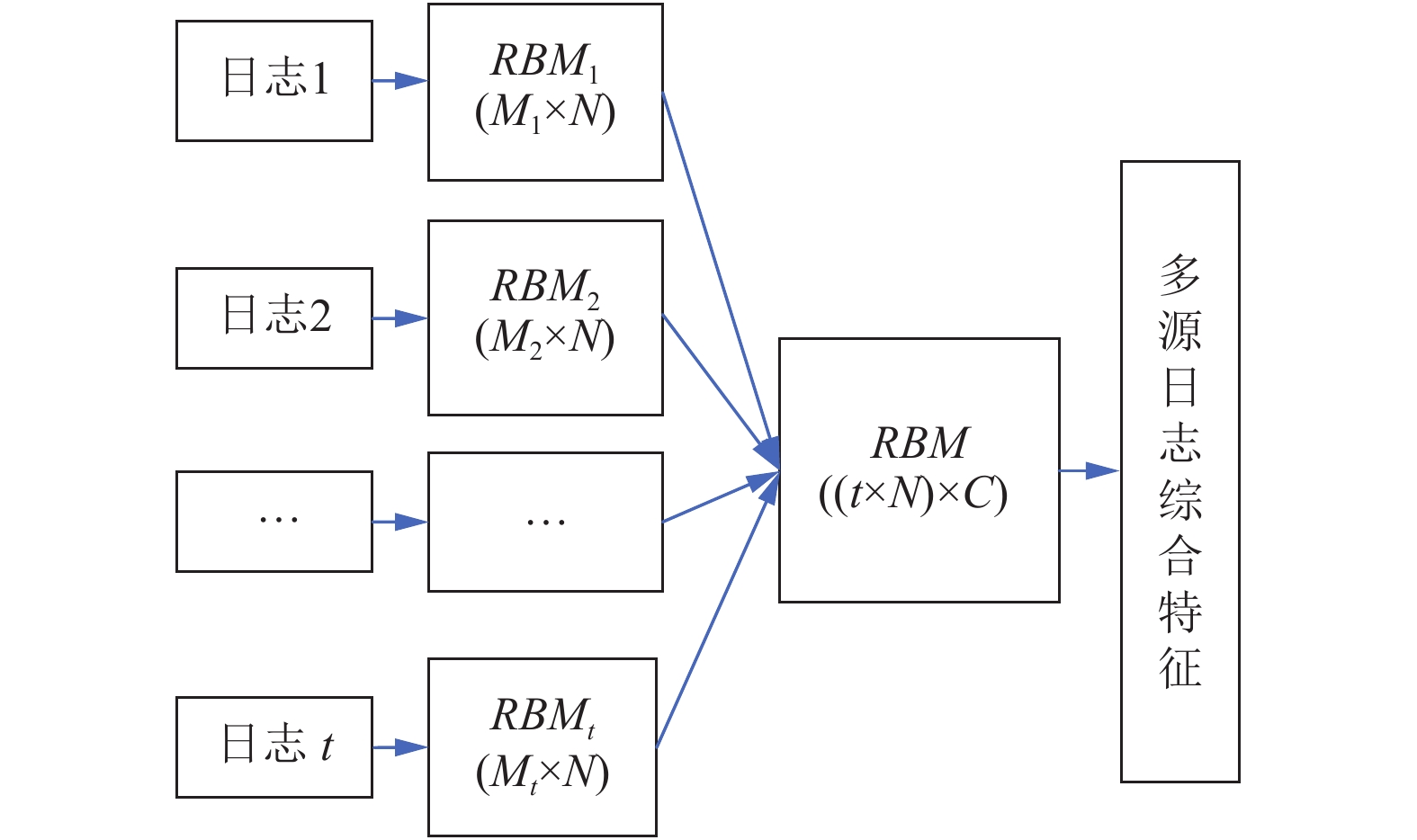
|
图 1 基于RBM的多源日志信息综合特征提取方法示意图 |
受限玻尔兹曼机(RBM)是一个随机神经网络,它包含一层可见层和一层隐藏层. 在RBM神经网络中通常事先设定隐藏单元数, 可见单元数赋值为训练数据的特征维数. 隐藏单元数目的设定, 通常采用训练集乘以单个数据的比特数, 进而采用低一个数量级的值设定为隐藏单元的数量[21]. 由于电力信息系统中数据冗余度较高, 因此可以使用更少一些的隐藏单元. 在本文方案中, N小于Mr的1/2以上. N的大小上限是与数据维度相关, 本文设定N的取值小于所有Mr的一半.
对于每类日志r, 训练相应的受限玻尔兹曼机神经网络RBMr. 训练的输入数据为日志r的数据, 从受限玻尔兹曼机神经网络RBMr的可见层神经元输入数据, 根据对比散度快速学习方法优化网络权值, 由此得到稳定的RBMr. 神经网络系统概率分布越集中, 则系统的能量越小. 能量函数的最小值, 对应着系统的最稳定状态. 通过调整网络的权值和偏置值使得网络对该输入数据的能量最低. 稳定状态是指当前的神经网络具有最小的能量.
2.3 训练学习RBM模型在RBM模型训练学习中, 采用对比散度快速学习方法和随机梯度上升法最大化对数似然函数对RBM模型进行训练学习, 通过对规范化编码后的日志信息进行处理. 对比散度快速学习方法优化网络权值的过程为: 可见层v和隐藏层h的神经元数目分别设为n和m, a和b分别为可见层和隐藏层的偏置向量, W为v和h之间的权值矩阵[22,23]. RBM对应的图是一个二分图, 层与层之间全部相连, 但层内的神经元之间没有连接线. 原始特征向量作为最底层的神经元的输入, 进而向RBM网络从下往上传递, 最后将提取到的特征向量转化成抽象的特征向量并对数据进行降维处理[23].
对于可见层v和隐藏层h, vi表示第i个可见单元的状态, hj表示第j个隐藏单元的状态; 从受限玻尔兹曼机神经网络可见层神经元输入数据, 根据神经元vi更新隐藏层神经元hj的状态; 再由隐藏层神经元hj重构出可见层神经元vi的状态, 接着再由重构出的可见层神经元vi的状态再重构出隐藏层神经元hj的状态, 完成一次受限玻尔兹曼机神经网络训练学习过程, 直到神经网络具有最小的能量值.
RBM是一种基于能量的模型, 所以我们可以使用能量函数来描述. 对于给定的状态(v, h), RBM具备的能量为:
| $ E\left( {v,h|\theta } \right) = - \sum\limits_{i = 1}^n {{a_i}{v_i}} - \sum\limits_{j = 1}^m {{b_j}{h_j}} - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{v_i}{W_{ij}}{h_j}} } $ | (1) |
其中,
| $ P\left( {v,h\mid \theta } \right) = \frac{{{e^{ - E\left( {v,h\mid \theta } \right)}}}}{{Z(\theta )}} $ | (2) |
其中,
由于RBM不同层的单元之间有连接, 而层内单元之间无连接. 因此, 当对可见单元的状态赋予确定的数值时, 各隐藏单元之间的激活状态相互独立[24-28]. 因此, 第j个隐藏单元的激活概率为:
| $ P\left( {{h_j} = 1\mid v,\theta } \right) = \omega \left( {{b_j} + \sum\limits_i {{v_i}} {W_{ij}}} \right) $ | (3) |
当对隐藏单元的状态赋予确定的数值时, 各可见单元的激活状态也相对独立, 则第i个可见单元的激活概率为:
| $ P\left( {{v_i} = 1\mid h,\theta } \right) = \omega \left( {{a_i} + \sum\limits_j {{h_j}} {W_{ij}}} \right) $ | (4) |
其中,
训练学习RBM的任务是计算参数
| $ {\theta ^*} = \arg \mathop {\max }\limits_\theta \zeta (\theta ) = \arg \mathop {\max }\limits_\theta \sum\limits_{t = 1}^T {\log } P\left( {{v^{(t)}}\mid \theta } \right) $ | (5) |
其中, T为包含的样本数.
为得到参数的最优值, 计算
| $ \zeta (\theta ) = \sum\limits_{t = 1}^T {\log } P\left( {{v^{(t)}}\mid \theta } \right) $ | (6) |
由于电力信息系统获得的观测数据(即训练样本数据)的特征维度通常较高, 因此对RBM的训练效率有更高的要求. 对比散度方法是一种快速学习方法, 方法处理开始时, 初始化一个训练样本并作为可见单元的状态输入, 随后再根据上述式(3)
| $ \Delta {W_{ij}} = \varepsilon \left( {{{\left\langle {{v_i}{h_j}} \right\rangle }_{\rm data}} - {{\left\langle {{v_i}{h_j}} \right\rangle }_{\rm recon}}} \right) $ | (7) |
| $ \Delta {a_i} = \varepsilon \left( {{{\left\langle {{v_i}} \right\rangle }_{{\rm {data}}}} - {{\left\langle {{v_i}} \right\rangle }_{{\rm {recon}}}}} \right) $ | (8) |
| $ \Delta {b_j} = \varepsilon \left( {{{\left\langle {{h_j}} \right\rangle }_{\rm data}} - {{\left\langle {{h_j}} \right\rangle }_{\rm recon}}} \right) $ | (9) |
其中,
当输入v时, 利用p(h|v)能计算出隐藏层h; 当计算出h时, 采用p(v|h) 又能计算出可视层, 通过不断调整参数, 使从隐藏层计算出的可视层v1与最初的可视层v相同, 则计算出的隐藏层即是可视层另外一种描述, 所以可以把隐藏层当作可视层输入数据的特征.
2.4 对比散度快速学习方法的优势本文在RBM模型训练学习中, 采用对比散度快速学习方法优化网络权值, 相对于其他典型网络权值优化方法[29-35]来说, 本文方法具有如下优势.
(1)对比散度快速学习方法克服了传统误差反向传播算法易陷于局部极值的问题, 是一种不依赖标签的无监督学习方法, 能够在无监督方法中自动从原始数据中学习特征.
(2)对比散度快速学习算法可以高效训练结构简单的马尔可夫随机模型(包括RBM), 每次训练只需要进行k次(一般就是1次)状态转移, 从而极大提升了训练效率.
(3)在对比散度快速学习中, 重复训练过程通过不断更新参数, 最后就能高效率地完成模型训练.
(4)对比散度快速学习算法使推荐模型能够包括异构内容信息, 例如文本、图像、音频甚至视频, 具有从多种来源学习的表现形式的潜力.
(5)对比散度快速学习技术具有很高的灵活性, 特别是随着许多流行的深度学习框架的出现, 如Tensorflow, Keras, Caffe, MXnet, DeepLearning4j, PyTorch, Theano等. 这些工具大多以模块化方式开发并具有活跃的社区和专业的支持, 良好的模块化使开发更有效率.
(6)对比散度快速学习算法可以很容易地将不同的神经网络结构组合起来以形成强大的混合模型, 因此, 我们可以轻松地构建混合和复合推荐模型, 以同时捕获不同的特征和因素.
2.5 数据降维方法及其优势本文RBM模型训练过程中, 通过利用随机梯度上升法最大化对数似然函数对RBM模型进行训练学习, 通过对规范化编码后的日志信息进行处理, 实现了数据降维并得到融合后的综合特征, 可以有效解决日志数据异构性带来的问题. 本文研究中采集的数据流量是公司网络出口处的全部数据流量, 包括各种安全日志、系统日志等信息, 需要处理的数据是多维的, 算法的时间复杂度与维数成指数级增加, 因此就需要进行降维处理[36-38].
在特征降维技术中主成分分析方法(Principal Component Analysis, PCA)是最为经典和实用的特征降维技术, 主成分分析的基本思想是通过构造原变量的一系列线性组合形成几个综合指标, 以去除数据的相关性, 并使低维数据最大程度保持原始高维数据的方差信息[39-41]. 我们通过对综合日志特征进行降维, 实现了数据降维, 从而使数据集更容易使用, 降低算法的计算开销, 去除数据噪声, 减轻过拟合, 也就更容易获取有价值的信息. 我们通过对特征加权, 特征越重要, 所赋予的权值就越大, 而不太重要的特征赋予较小的权值, 模型中对每一个特征都赋予了一个权值, 从而有效保障了日志信息的完整性.
数据降维分为特征选择和特征提取两种方法, 文中采用的是特征提取方法, 即经已有特征的某种变换获取简约特征. 通过采用变换(映射)的方法, 把原始特征变换为较少的新特征, 由原始数据创建新的特征集, 从而有效提取出网络攻击等特征信息.
3 基于RBM的多源日志信息综合特征提取系统利用上述RBM的训练学习方法, 构建用于提取综合特征的受限玻尔兹曼机神经网络RBMcom, RBMcom为两层网络, 可见层节点数为t×N, 隐藏层节点数为C, 随机产生[0,1]之间的随机数作为神经网络的连接权值, 初始化RBMcom. 基于RBM的多源日志信息综合特征提取系统构建如图2所示.
对第一层受限玻尔兹曼机神经网络RBMr隐藏层输出的数据进行拼接组成数据序列, 将所述数据序列作为训练输入数据对受限玻尔兹曼机神经网络RBMcom进行训练, 所述数据序列的维度为t*N, 根据对比散度快速学习方法优化网络权值, 由此得到稳定的RBMcom. 基于训练好的受限玻尔兹曼机神经网络集合{ RBM1, RBM2, ···, RBMt, RBMcom }, 构建多源日志综合特征提取系统. 基于RBM的多源日志信息综合特征提取算法详细过程如算法1所示.
在算法1中, 通过将从电力信息系统采集的各类日志数据输入相应的受限玻尔兹曼机神经网络, 经过不断训练学习, 构建多源日志综合特征提取系统, 再将各类日志数据输入RBM神经网络训练即可获得维度为C的综合特征数据.
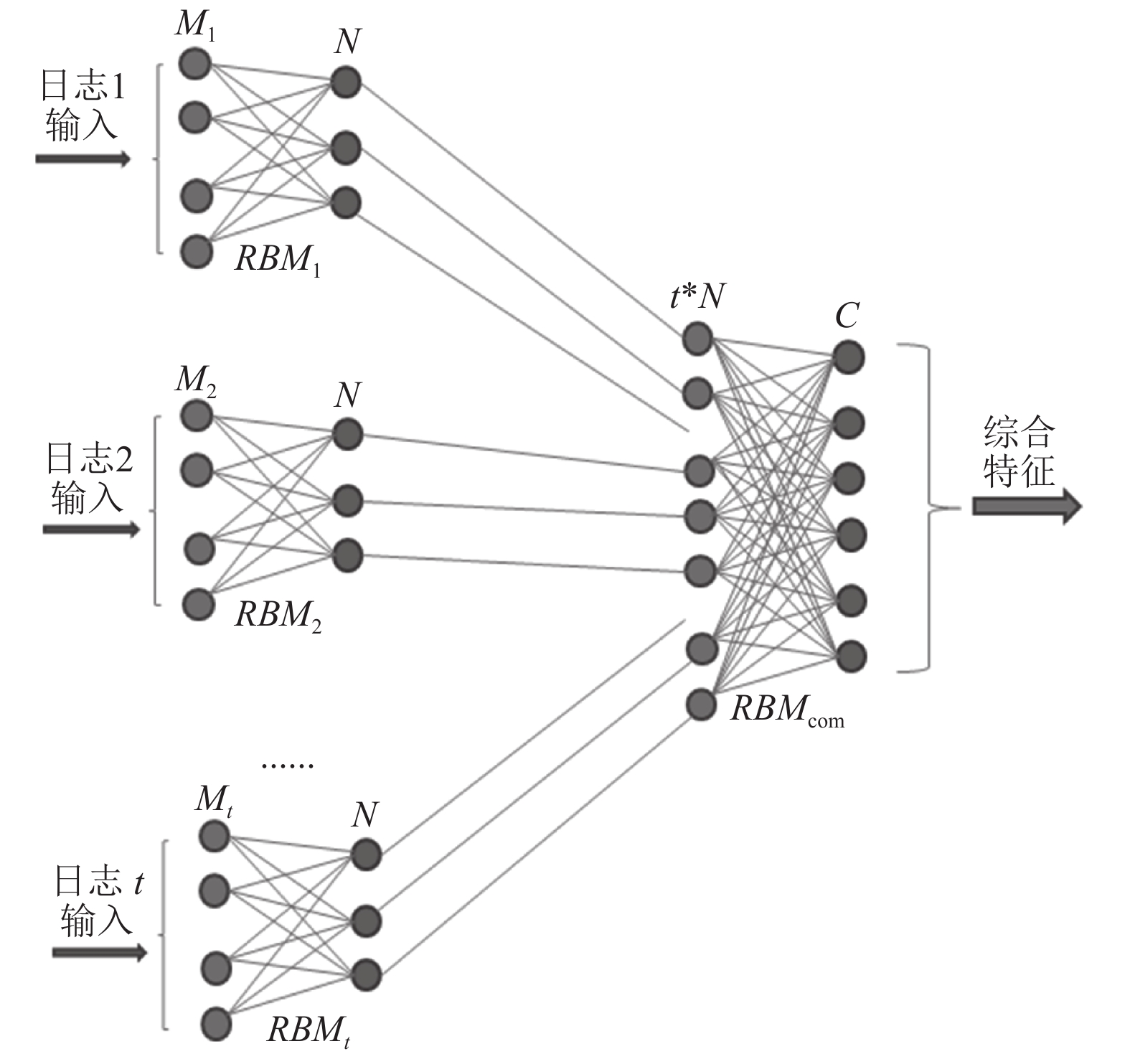
|
图 2 基于RBM的多源日志信息综合特征提取系统 |
4 实验结果与分析
为了验证基于RBM的多源日志综合特征提取方法的有效性, 本文以某电力公司的网络安全日志数据为例, 测试本文算法的有效性. 实验采用的日志数据主要包括公司内外网IDS、IPS、防火墙、防病毒系统和数据库访问日志等.
我们基于前期研究搭建的电力系统中基于大数据的网络安全态势感知预警平台[42], 目前接入公司信息内外网共计43套信息系统重点资产作为监控对象. 平台已采集公司威胁事件数据30TG, 记录攻击威胁条数8160兆条. 采集的日志信息样本集包括: 攻击触发时间、攻击威胁类型、危险等级、安全设备、客户单位、攻击源IP、攻击目标IP. 采集的日志信息样本类型如表1所示.
| 表 1 日志信息样例 |
通过利用基于RBM的多源日志综合特征提取方法对采集的安全日志信息进行训练学习, 提取的攻击类型包括: Web攻击、IPS、特征值警报、可疑域名、黑IP警报、邮件敏感字、攻击事件-SCAN、攻击事件-DDOS等. 通过对提取的攻击特征进行分析, 若有攻击则通过预警平台前端页面进行实时展示.
本实验中, 通过对公司内外网重点资产的攻击日志进行实时监测分析, 当监控到有IP地址在对公司系统进行持续攻击并多次触发高危报警, 便可以对该IP的攻击行为进行回溯取证, 根据提取的日志特征研判攻击类型, 从而预测预警公司的网络安全态势. 通过定位到该IP地址攻击行为的所有数据包, 然后下载该攻击数据包, 对攻击过程进行还原. 实验环境下监测到2019年11月的Top IP前10个主机总流量如图3所示, 攻击数据包的信息如图4所示.

|
图 3 Top IP主机总流量 |

|
图 4 攻击数据包信息 |
通过对攻击数据包的通信协议进行分析研判发现, IP地址114.254.131.230, TCP端口号为41731的主机对IP地址为: 123.232.5.62, TCP端口号为80的攻击是一主机被植入了木马. 通过查看详细的TCP信息发现, 可进一步提取该主机的passwd敏感路径信息, 如图5所示. 通过对受感染的终端进行具体定位, 发现为某用户上网时不慎导致木马感染, 之后立即对该木马进行清除, 并在全公司范围内下发安全预警进行排查, 对发现的隐患进行全面消缺.

|
图 5 提取攻击特征找到被植入木马的主机 |
实验环境中, 通过威胁预警平台对安全设备日志特征进行提取分析, 以实验平台中2019年10月和11月的数据为例, 各类威胁次数排名Top5的对比分析如图6所示.

|
图 6 威胁类型次数排名Top5的对比分析 |
图6中, 竖轴中的k表示1000次. 图7展示了近30天内被攻击的Top1资产系统, 统计了月度内的威胁事件总数和攻击源IP等信息. 从公司重点资产安全态势中能够清晰地展示各业务系统面临的威胁, 进而定位被攻击资产并进行隐患消缺.

|
图 7 近30天攻击Top1及威胁事件总数 |
5 结论
随着“大云物移智链”信息新技术与电网业务的深度融合应用, 网络攻击威胁越来越多. 本文利用电网信息系统中安全日志信息中的异构数据源, 研究了基于受限玻尔兹曼机的电力大数据多源日志综合特征提取方法. 通过采用受限玻尔兹曼机神经网络对各类日志信息进行规范化编码, 有助于解决日志数据异构性带来的问题; 进而再用受限玻尔兹曼机神经网络对规范化编码后的日志信息进行处理, 可以实现降维并得到融合后的综合特征. 最后通过在电力信息系统中搭建大数据预警监测实验环境, 验证本文的日志综合特征提取方法对威胁检测的效果. 实验结果表明, 本文提出的方法在提取电力信息系统中日志特征时具有较高的准确率, 进而提高了网络安全态势预测的速度和预测精度.
| [1] |
薛禹胜, 赖业宁. 大能源思维与大数据思维的融合(一)大数据与电力大数据. 电力系统自动化, 2016, 40(1): 1-8. DOI:10.7500/AEPS20151208005 |
| [2] |
赖特. 网络安全设备日志融合技术研究[硕士学位论文]. 成都: 电子科技大学, 2015.
|
| [3] |
黄新平. 政府网站信息资源多维语义知识融合研究[博士学位论文]. 长春: 吉林大学, 2017.
|
| [4] |
王秀锋. 网络环境下异构日志信息获取和预处理研究[硕士学位论文]. 哈尔滨: 哈尔滨工程大学, 2010.
|
| [5] |
酆勇, 熊庆宇, 石为人, 等. 一种基于受限玻尔兹曼机的说话人特征提取算法. 仪器仪表学报, 2016, 37(2): 256-262. DOI:10.19650/j.cnki.cjsi.2016.02.003 |
| [6] |
陈龙, 周剑, 王国胤. 融合多源日志辅助取证的事件场景关联方法. 重庆邮电大学学报(自然科学版), 2007, 19(5): 584-589. |
| [7] |
江雨燕, 桂伟. 基于受限玻尔兹曼机的分布式主题特征提取. 计算机工程与应用, 2017, 53(23): 108-112. DOI:10.3778/j.issn.1002-8331.1706-0214 |
| [8] |
程乐峰, 余涛, 张孝顺, 等. 机器学习在能源与电力系统领域的应用和展望. 电力系统自动化, 2019, 43(1): 15-31. |
| [9] |
刘凯, 张立民, 周立军. 随机受限玻尔兹曼机组设计. 上海交通大学学报, 2017, 51(10): 1235-1240. DOI:10.16183/j.cnki.jsjtu.2017.10.013 |
| [10] |
杨杰, 孙亚东, 张良俊, 等. 基于弱监督学习的去噪受限玻尔兹曼机特征提取算法. 电子学报, 2014, 42(12): 2365-2370. DOI:10.3969/j.issn.0372-2112.2014.12.005 |
| [11] |
沈卉卉, 李宏伟. 基于动量方法的受限玻尔兹曼机的一种有效算法. 电子学报, 2019, 47(1): 176-182. DOI:10.3969/j.issn.0372-2112.2019.01.023 |
| [12] |
康丽萍, 许光銮, 孙显. 受限玻尔兹曼机的稀疏化特征学习. 计算机科学, 2016, 43(12): 91-96. DOI:10.11896/j.issn.1002-137X.2016.12.016 |
| [13] |
罗恒. 基于协同过滤视角的受限玻尔兹曼机研究[博士学位论文]. 上海: 上海交通大学, 2011.
|
| [14] |
何洁月, 马贝. 利用社交关系的实值条件受限玻尔兹曼机协同过滤推荐算法. 计算机学报, 2016, 39(1): 183-195. DOI:10.11897/SP.J.1016.2016.00183 |
| [15] |
高琰, 陈白帆, 晁绪耀, 等. 基于对比散度-受限玻尔兹曼机深度学习的产品评论情感分析. 计算机应用, 2016, 36(4): 1045-1049. DOI:10.11772/j.issn.1001-9081.2016.04.1045 |
| [16] |
郑志蕴, 李步源, 李伦, 等. 基于云计算的受限玻尔兹曼机推荐算法研究. 计算机科学, 2013, 40(12): 259-263. DOI:10.3969/j.issn.1002-137X.2013.12.056 |
| [17] |
张俊玲, 陈志刚, 许旭, 等. 基于改进卷积受限玻尔兹曼机的滚动轴承故障诊断. 组合机床与自动化加工技术, 2019(5): 73-76. DOI:10.13462/j.cnki.mmtamt.2019.05.018 |
| [18] |
张立民, 刘凯. 基于深度玻尔兹曼机的文本特征提取研究. 微电子学与计算机, 2015, 32(2): 142-147. DOI:10.19304/j.cnki.issn1000-7180.2015.02.033 |
| [19] |
谈建慧, 景新幸, 杨海燕. 深度信念网络的Bottleneck特征提取方法. 桂林电子科技大学学报, 2016, 36(2): 118-122. DOI:10.16725/j.cnki.cn45-1351/tn.2016.02.007 |
| [20] |
闫琰. 基于深度学习的文本表示与分类方法研究[博士学位论文]. 北京: 北京科技大学, 2016.
|
| [21] |
米龙. 自适应深度学习算法在目标分类问题中的应用[硕士学位论文]. 沈阳: 东北大学, 2014.
|
| [22] |
孙劲光, 蒋金叶, 孟祥福, 等. 深度置信网络在垃圾邮件过滤中的应用. 计算机应用, 2014, 34(4): 1122-1125. |
| [23] |
毛冬. 大数据下风电机组发电机故障预警方法的研究[硕士学位论文]. 北京: 华北电力大学, 2016.
|
| [24] |
张春霞, 姬楠楠, 王冠伟. 受限波尔兹曼机. 工程数学学报, 2015, 32(2): 159-173. DOI:10.3969/j.issn.1005-3085.2015.02.001 |
| [25] |
吴志宇. 基于深度学习的稀疏化电能质量扰动识别方法研究[硕士学位论文]. 成都: 西南交通大学, 2019.
|
| [26] |
周博曦, 秦晋, 王金亮, 等. 基于人工神经网络与有限状态机的变电站告警处理系统. 山东电力技术, 2020, 47(1): 6-13. |
| [27] |
张廷忠, 张庆辉, 邢强, 等. 基于LMD与GA-BP神经网络组合的短期风速滚动预测方法. 山东电力技术, 2019, 46(11): 13-20. DOI:10.3969/j.issn.1007-9904.2019.11.003 |
| [28] |
田怀源, 张峰, 王新库, 等. 基于灰色关联度和BP神经网络的最大负荷同时率预测方法研究. 山东电力技术, 2017, 44(4): 11-15, 21. DOI:10.3969/j.issn.1007-9904.2017.04.003 |
| [29] |
Chen R, Ren ZW, Meng ZH, et al. Oblique-incidence reflectivity difference method combined with deep learning for predicting anisotropy of invisible-bedding shale. Energy Reports, 2020, 6: 795-801. |
| [30] |
Velasco JA, Amaris H, Alonso M. Deep Learning loss model for large-scale low voltage smart grids. International Journal of Electrical Power & Energy Systems, 2020, 121: 106054. DOI:10.1016/j.ijepes.2020.106054 |
| [31] |
Zheng WY, Huang WJ, Hill DJ. A deep learning-based general robust method for network reconfiguration in three-phase unbalanced active distribution networks. International Journal of Electrical Power & Energy Systems, 2020, 120: 105982. DOI:10.1016/j.ijepes.2020.105982 |
| [32] |
Krishnan R, Jagannathan S, Samaranayake VA. Direct error-driven learning for deep neural networks with applications to big data. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(5): 1763-1770. DOI:10.1109/TNNLS.2019.2920964 |
| [33] |
Li HL, Weng J, Shi YJ, et al. An improved deep learning approach for detection of thyroid papillary cancer in ultrasound images. Scientific Reports, 2018, 8(1): 6600. DOI:10.1038/s41598-018-25005-7 |
| [34] |
Chen CLP, Feng S. Generative and discriminative fuzzy restricted Boltzmann machine learning for text and image classification. IEEE Transactions on Cybernetics, 2020, 50(5): 2237-2248. DOI:10.1109/TCYB.2018.2869902 |
| [35] |
Chu JL, Wang HJ, Meng H, et al. Restricted boltzmann machines with Gaussian visible units guided by pairwise constraints. IEEE Transactions on Cybernetics, 2019, 49(12): 4321-4334. DOI:10.1109/TCYB.2018.2863601 |
| [36] |
Park CH, Lee GH. Comparison of incremental linear dimension reduction methods for streaming data. Pattern Recognition Letters, 2020, 135: 15-21. DOI:10.1016/j.patrec.2020.03.028 |
| [37] |
Washington P, Paskov KM, Kalantarian H, et al. Feature selection and dimension reduction of social autism data. Pacific Symposium on Biocomputing, 2020, 25: 707-718. |
| [38] |
Choi JY, Kyung M, Hwang H, et al. Bayesian extended redundancy analysis: A Bayesian approach to component-based regression with dimension reduction. Multivariate Behavioral Research, 2020, 55(1): 30-48. DOI:10.1080/00273171.2019.1598837 |
| [39] |
Xu C, Yang M, Zhang J. Fast deflation sparse principal component analysis via subspace projections. Journal of Statistical Computation and Simulation, 2020, 90(8): 1399-1412. DOI:10.1080/00949655.2020.1728761 |
| [40] |
Sanchez J, Denis F, Coeurjolly D, et al. Robust normal vector estimation in 3D point clouds through iterative principal component analysis. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, 163: 18-35. DOI:10.1016/j.isprsjprs.2020.02.018 |
| [41] |
Zhang X, He L, Zhang J, et al. Determination of key canopy parameters for mass mechanical apple harvesting using supervised machine learning and Principal Component Analysis (PCA). Biosystems Engineering, 2020, 193: 247-263. DOI:10.1016/j.biosystemseng.2020.03.006 |
| [42] |
刘冬兰, 刘新, 张昊, 等. 基于大数据的网络安全态势感知及主动防御技术研究与应用. 计算机测量与控制, 2019, 27(10): 229-233. DOI:10.16526/j.cnki.11-4762/tp.2019.10.047 |
 2020, Vol. 29
2020, Vol. 29


