2. 国电南瑞南京控制系统有限公司, 南京 211106
2. NARI Nanjing Control System Co. Ltd., Nanjing 211106, China
国家电网公司各省级计量中心自动化检定系统的建设有效解决了智能电能表大批量安装应用及更新换代的需求, 有力推进了电能计量生产管理模式和管控流程向集约化、自动化、标准化、智能化方向发展[1,2]. 自动化检定流水线依托智能库房推动生产业务流转, 实现电能计量器具的库存管理、出入库、检定上下料、外观检查、耐压试验、检定检测、封印贴标等[3]. 但由于各流水线系统之间的生产控制策略彼此独立, 容易出现拥塞和饥饿现象[4], 导致各自动化系统之间的实时生产协同及故障异常处理工作主要还是依赖人工管理经验, 且系统持续的长期运转现状容易发生多种机械或电气故障, 生产故障不易发现、发现不易处理, 严重影响了生产效率, 也对自动化生产设备造成安全隐患. 因此, 开展对自动化检定流水线故障诊断的研究, 准确、及时地发现系统的故障并进行控制和排除, 对保证计量检定平稳、安全生产具有重要意义.
目前, 国内外在自动化检定流水线故障诊断方面的研究较少. 实际生产环境中主要依靠各设备系统厂家在关键环节安装传感器采集故障信息, 信息监测点较少, 故障判断方法单一, 故障源分辨率粗糙. 浙江省电力公司在计量自动化检定系统的研发应用过程中, 提出了结合离线静态、在线动态和质量抽查等监控方式, 实现了基本的流水线异常监控, 并进行了探索应用. 吉林省电力公司就智能电能表自动化检定系统的技术特点进行了管理层面上的探索, 提出建立专业的运维队伍、制定完善的运行和文档管理制度等管理要求. 国电南瑞在省级计量生产调度平台建设过程中, 初步实现了计量生产设施的基本管理功能, 涵盖了设施的采购、投运前、台账、维护、巡检、故障、报废、备品备件等方面的管理, 对自动化检定系统的故障信息进行了统一汇总和集中存储, 并进行了初步的故障分析. 国外在电能表技术标准方面主要以IEC (国际电工委员会)、美国ANSI C12和日本JIS C12为代表[5], 但是在高度自动化、流程化的大规模自动化检定检测流水线应用及故障诊断方面未见明确报道.
本文在自动化检定流水线各检定单元之间的物理连接关系、故障传播关系以及它们的相互作用机理研究基础上, 针对自动化检定流水线生产故障不易发现、发现不易处理等问题, 引入一种基于分层符号有向图(HSDG)[6,7]的故障诊断方法; 并结合动态核偏最小二乘支持向量回归(DKPLS-SVR)模型[8,9]提出离线分析和在线诊断过程. 最后将该方法应用于单相电能表自动化检定流水线进行故障识别与诊断, 提高故障诊断效率和诊断精度.
1 SDG基本概念及数学模型 1.1 SDG的基本概念符号有向图(Signed Directed Graph, SDG)[10,11], G={V, E}, 其中V={vi}表示节点集, 节点符号Ψ(vi)∈SV(SV表示符号集); E={ek}表示有向边集, 有向边表示为ek=(vi, vj)或ek=vi→vj且其符号φ(ek)∈{+, –}. 文章中使用三状态SDG即GSDG3, 定义SV={+, 0, –}, 分别表示超高, 正常和超低状态; 路径φ(vi, vj)∈{+, –}, 分别表示增量作用与减量作用, 在GSDG3中, φ(vi, vj)=+表示vi±→vj±, φ(vi, vj)= –表示vi±→vj∓; 通常用实线代表增量作用, 用虚线代表减量作用.
在自动化检定流水线中, 将系统所有关键影响因素定义为SDG的节点集V, 该节点集在建模前期由人工梳理确定并定义节点类型. 在时间点t采集到所有节点值, 然后根据各节点阈值计算节点状态, 即获得系统在t时刻的样本S.
如图1所示, 自动化检定系统在运行时刻t采集到样本S, 该样本中有3个节点A、B、C, 其中A、B超过正常阈值, 用“+”表示, C低于正常阈值, 用“–”表示; 图中以实线、虚线表示两种支路关系, 节点A、B间正影响, 节点A、C间负影响. 在样本S中, 如果节点符号不为零则该节点即为有效节点; 如果Ψ(vi)φ(ek)Ψ(vj)=+, 则该支路ek称为相容支路, 由相容支路组成的路径称为相容路径.

|
图 1 SDG结构示意图 |
在瞬时样本S中, 依据相容路径的规则找出所有符合逻辑关系的路径. 在相容路径中, 从初始节点的状态偏离开始, 影响其邻接下游节点的状态偏离, 并一直延伸至末端节点; 但在非相容路径中, 节点间的状态偏离与其连接支路的状态不符合逻辑关系(即无效节点), 因此相容路径才是系统故障进行传播和演变的通道. 所以, 通过搜索样本中的所有相容路径, 即可得出系统故障的因果图, 进而推论出复杂系统内部的故障发展演变过程.
1.2 SDG的数学模型为了方便描述SDG模型, 一般将有向图以矩阵的形式存储在计算机中. 在图论中, 一般借助邻接矩阵和可达矩阵两种形式表示有向图[9].
有向图的邻接矩阵表示: 有向图G={V, E}的邻接矩阵表示为A=(Aij)n×n, n为节点个数, 其中的元素Aij为:
| $ {A_{ij}} = \left\{ \begin{array}{l} 1, \quad {\text{两节点间存在直接有向边}}\\ 0, \quad {\text{两节点间不存在直接有向边}} \end{array} \right. $ | (1) |
有向图的可达矩阵表示: 有向图G={V, E}的可达矩阵表示为P=(Pij)n×n, n为节点个数, 其中的元素Pij为:
| $ {P_{ij}} = \left\{ \begin{array}{l} 1, \quad {\text{节点}}{v_i}{\text{到}}{v_j}{\text{至少存在一条有向路径}}\\ 0, \quad {\text{节点}}{v_i}{\text{到}}{v_j}{\text{不存在有向路径}} \end{array} \right. $ | (2) |
在节点数量较少时, 可以通过直接观察得到邻接模型的邻接矩阵和可达矩阵, 当节点数目较多时, 邻接矩阵A可通过Warshall算法[10,12]转化为可达矩阵P.
2 基于HSDG模型的故障诊断方法 2.1 系统分层步骤系统分层方法如下:
① 依据SDG得到系统S的邻接矩阵Aij(i, j=[1, 2, 3, ···, n]).
② 判断系统S是否可分层, 若可分层, 则继续执行③; 若不可分层, 则退出.
③ 利用Warshall算法将邻接矩阵Aij转化为可达矩阵Pij.
④ 分别提取可达矩阵Pij的第i行、第i列中所有值为1的元素对应的行节点、列节点, 分别得到可达集Ri、先行集Ai, 计算其交集Ri∩Ai; 若节点vi满足Ri∩Ai=Ai, 则该节点就是第一层中的节点; 循环计算所有的节点, 得到第一层节点集.
⑤ 将可达矩阵Pij中已被分配到高层的所有节点移除, 得到一个新的可达矩阵.
⑥ 重复执行步骤④, 将所有节点处理完成后, 得到各层的节点集, 即可建立新的符号有向图HSDG.
2.2 DKPLS-SVR模型的应用应用标准最小二乘支持向量回归(LS-SVR)模型算法在求解样本为N的问题时, 需要对N+1阶的矩阵求逆, 随着样本量的增加其计算复杂度急剧增大, 且其对拟合输出值的反复计算同样会加剧运算效率的降低[13]. 目前, 已有的研究结果表明, 如果样本维度过大, 会导致标准LS-SVR运行算法的计算机内存溢出, 无法解决大样本的回归学习[14].
而在执行基于SDG的故障诊断过程中, 针对样本中各节点的有效性判断都必须基于测量值与其上限和下限进行比较以识别偏差. 如果样本中存在n个变量, 则系统必须指定2n个阈值; 然而, 阈值的确定因涉及大量参数间关联性分析且缺乏明确的规则, 在工程应用中是一个很难实现的过程. 通常, 系统都是基于用户经验, 在观测变量平均值的基础上初始化恒定的正负偏差以作限值, 但此类固定限值又因信燥影响而导致大量误判而发出预警. 因此, 为克服以上问题, 在标准LS-SVR模型的基础上引入动态核偏最小二乘支持向量回归(DKPLS-SVR)模型以提高SDG中各变量特征提取能力. 通过建立一系列DKPLS-SVR模型来估计系统中目标测量变量的值, 估计值与测量值之间的残差可以用来确定变量的定性状态及故障征兆, 进而引导SDG推理.
2.3 基于HSDG的流水线故障诊断方法在分层符号有向图模型HSDG中, 既保留了原SDG模型的完整信息, 又明确了节点间的空间层次, 可依据前述的相容性定义开展判断. 根据自动化检定流水线的特性, 完整的算法流程如图2及图3所示.

|
图 2 自动化检定流水线故障诊断的完整流程(离线分析) |
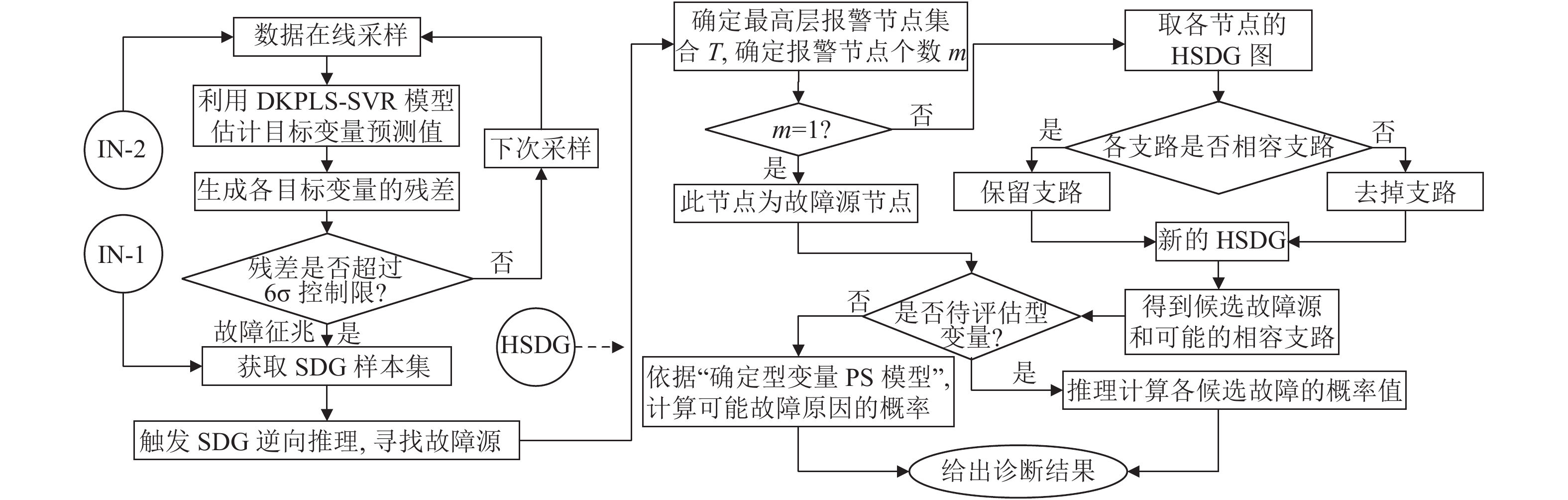
|
图 3 自动化检定流水线故障诊断的完整流程(在线诊断) |
该故障诊断流程主要由离线分析和在线诊断两部分组成, 其中离线分析功能包含系统SDG模型建立、HSDG模型分层、目标变量分类(基于检定流水线“流量”监控的待评估型变量和基于告警的确定型变量)、确定型变量概率PS模型建立; 在线诊断功能包含在线数据采样、待评估型变量DKPLS-SVR残差计算、SDG逆向推理、诊断结果输出. 关于故障诊断推理的主要思想是: 对待评估型变量和确定型变量执行反向推理时, 依据相容性判据, 将其放入后续节点集中作为有效节点; 此方法能尽可能降低后续推理负担并减少冗余, 与常见的广度优先搜索、深度优先搜索相较更符合本自动化检定流水线故障演变的特点.
3 自动化检定线的HSDG模型及案例验证 3.1 系统物理结构及影响因素分析如图4所示, 是一条单相电能表自动化检定流水线的物理组成示意图. 其中, 根据实际设计指标及生产经验, 把表计除尘装置、信息绑定装置、封印验证装置、二维码验证装置看做一个整体, 把检定装置01-10看做一个整体.
故障诊断的准确性和及时性依赖相关信息数据采集频度和数据采集密度, 数据采集质量又依靠传感器的布置情况, 大量传感器布置, 可为故障诊断提供较多的数据基础, 但同时也引入了大量冗余数据, 降低了故障的分辨率, 且加重了硬件设备PLC层和软件系统层的数据处理压力. 这在一定程度上会影响检定生产作业的效率, 违背自动化检定流水线设计初衷. 因此, 自动化检定流水线目前只在关键生产节点安放传感器进行信息采集, 能够满足目前的生产运行现状. 在不增加或只是局部少量增加传感器的情况下, 采用一种改进的分层符号有向图(HSDG)故障诊断方法进行自动化检定流水线故障诊断, 该故障诊断基于前文介绍的两种类型目标变量观测样本, 一是根据历史故障信息和故障原因信息对设备主动上报的故障现象(即确定型变量)进行故障原因判断, 给出候选故障原因的优先级及概率; 二是基于故障征兆(即待评估型变量)的故障判断, 根据采样点的数据偏差推理故障发生原因.

|
图 4 自动化检定流水线物理结构 |
单相电能表自动化检定系统中任何子设备的故障都可能使检定性能下降甚至使系统停机, 因此在建立单相电能表自动化检定系统SDG模型时, 不仅要考虑各子设备实际的物理连接情况, 还要根据系统对诊断准确度的要求合理分析各子设备之间相互影响及子设备自身因素的影响. 根据系统运行维护经验及系统物理结构梳理出各子设备的影响因素, 具体如下(因篇幅所限, 只例举上料装置A):
A01: 立库出库情况;
A02: 空托盘缓存情况;
A03: 空箱缓存情况;
A04: 机器人抓表情况;
A05: 上料箱输送情况.
可见, 每个装置都由一个或多个影响因素与之关联, 每个影响因素还存在多种可能的故障原因, 以“A04-机器人抓表情况”为例, 其可能的故障原因见表1.
| 表 1 “A04-机器人抓表情况”的故障原因 |
3.2 系统建模及HSDG模型分层
通过分析单相电能表自动化检定流水线系统结构可以建立单相检定线的SDG模型, 如图5所示. 各节点说明如表2所示(其中, 节点类型: 1-确定型; 2-待评估型).

|
图 5 自动化检定流水线SDG模型图 |
依据2.1章节的系统分层步骤对图5进行分层:
① 根据图5的SDG模型, 获得系统的邻接矩阵A35×35;
② 判断系统可分层, 并利用Warshall算法计算其可达矩阵P35×35;
③ 计算得第一层节点为{2, 4, 5, 6, 8, 9, 10, 11, 15, 16, 18, 19, 21, 24, 25, 27, 29, 31, 32, 33, 35};
④ 去除第一层节点, 得到一个新的可达矩阵P14×14, 重复以上步骤, 可得到第二层节点为{03, 34}.
| 表 2 SDG模型节点说明 |
3.3 案例验证
分层符号有向图HSDG中的节点都是可观测的, 下面通过几种典型场景下的测量数据进行故障诊断说明.
(1)场景1. 上料机器人抓表异常
当单相电能表自动化检定系统上料异常时, 以上观测点的SDG模型样本数据集如下:
节点编号集=(01, 05, 06, 07, 02, …), 则其对应的节点符号集=(–, –, 0, –, 0, …).
由样本数据可知, 二维码验证装置出口流量下降, 上料装置出口流量下降, 机器人抓表出现异常. 由此偏离样本数据并结合图5的分层符号有向图HSDG, 可得到样本的最高层报警节点集T1={05}. 由场景1的样本数据得到的最高层报警节点为“05”, 该节点为根节点, 即为报警源, 且已知其节点类型为确定型. 再根据表1, 该报警源对应的可能故障原因有8种, 结合历史告警数据使用式(3)进行故障原因概率计算, 给出故障原因排序.
| $p({s_i}) = \frac{{k({s_i})}}{{\displaystyle\sum\limits_{i = 1}^n {k({s_i})} }} \times 100\% $ | (3) |
其中, n为某一种报警现象对应的报警原因数量, n≥1; k(si)为第i种报警原因历史统计总数, 1≤i≤n .
场景1的故障诊断最终结果排序见表3.
| 表 3 报警原因概率 |
(2)场景2. 外观识别装置出口流量下降
通过实时观测数据, 发现外观识别装置出口流量下降超出阈值, 获取样本信息数据集如下:
节点编号集=(07, 12, 13, 14, 17, 20, 21, …), 对应的节点符号集=(+, +, –, +, –, –, 0, …).
由此偏离样本数据并结合图6的分层符号有向图HSDG, 可得到样本的最高层报警节点集T2={07, 12, 13, 14, 17, 20}. T2的SDG模型如图7(a)所示, 因Ψ(v14)φ(e14→20)Ψ(v20)= –, Ψ(v07)φ(e07→13)Ψ(v13)= –, 判断节点14→20和节点07→13为不相容支路, 去掉该两个有向边后得到新的SDG, 如图7(b)所示. 由图7(b)可得, 节点13为该SDG的根节点, 那么节点13为该样本的故障源节点, 即2号耐压装置的入口流量减少为故障源. 因此, 可据此判断2号耐压装置缓存区域有可能出现托盘卡壳现象.

|
图 6 单相自动化检定流水线HSDG模型图 |

|
图 7 场景2样本的推理SDG |
(3)场景3. 下料装置出口流量下降
通过实时观测数据, 发现下料装置出口流量下降超出阈值, 获取样本信息数据集如下:
节点编号集=(04, 28, 30, 31, 34, 32, …), 则其对应的节点符号集=(–, +, –, –, –, 0, …).
由此偏离样本数据并结合图6的分层符号有向图HSDG, 可得到样本的最高层报警节点集T3={04, 28, 30, 31, 34}. T3的SDG模型如图8(a)所示, 因Ψ(v28)φ(e28→30)Ψ(v30)= –, 判断节点28→30为不相容支路, 去掉该有向边后得到新的SDG, 如图8(b)所示.
由图8(b)可得节点04和节点31为可能的故障源节点, 即下料位的空箱不足或立库未执行入库操作导致下料装置下料缓慢. 进一步, 若根据历史统计信息, 可计算这两个故障源节点的概率大小.
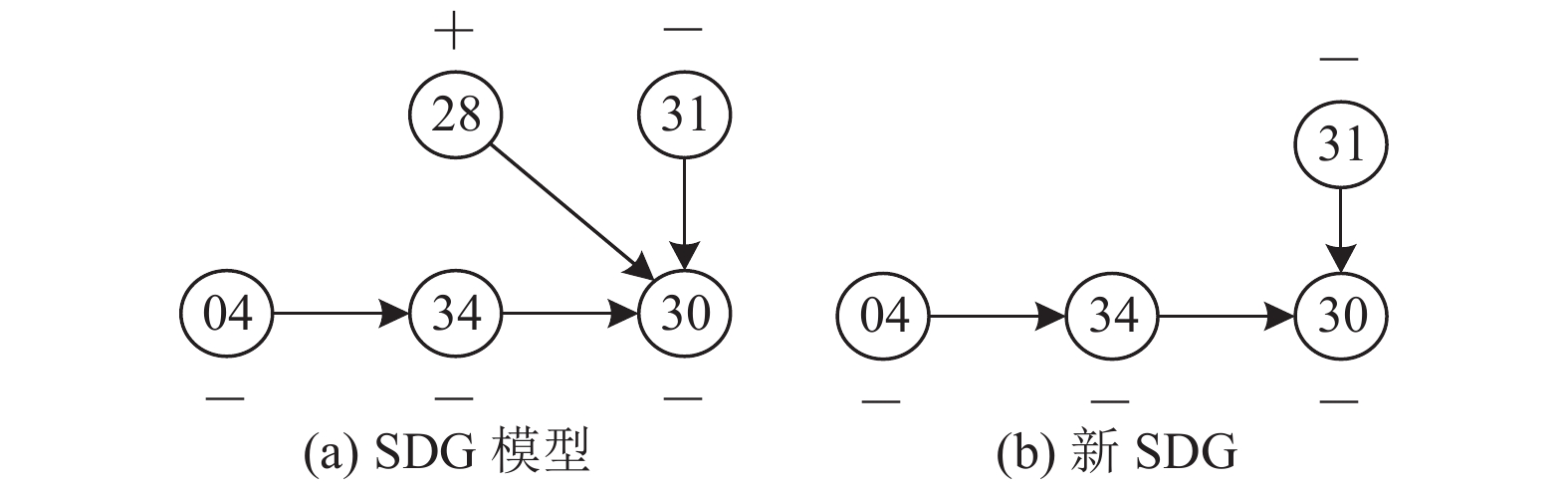
|
图 8 场景3样本的推理SDG |
4 结 论
本文针对省级计量中心自动化检定流水线故障在线诊断开展研究, 引入SDG方法建立适用于自动化检定流水线的分层符号有向图模型, 并结合定量方法对各采样节点进行SDG符号判断, 输出诊断模型样本. 设计了一套完整的基于“离线分析”和“在线诊断”的故障诊断流程. 通过实例场景分析, 验证了分层SDG故障诊断方法在自动化检定流水线故障诊断中的可行性与准确性, 且该方法能规避无效节点, 故障辨识能力强, 具有鲁棒性, 其诊断结果具备一定的解释能力.
| [1] |
陈欢军, 鲁然, 陈伊娜, 等. 2018全国重点能源资源计量服务示范项目之五电能表智能化计量检定技术研发及应用. 中国计量, 2019(7): 39-43. |
| [2] |
张燕, 黄金娟. 电能表智能化检定流水线系统的研究与应用. 电测与仪表, 2009, 46(12): 74-77. DOI:10.3969/j.issn.1001-1390.2009.12.018 |
| [3] |
孙丽娜, 刘晓泽, 吴晓光, 等. 智能电表自动化检定流水线运行状态检测技术应用. 国外电子测量技术, 2018, 37(8): 77-81. |
| [4] |
黄友朋, 方彦军, 唐猛, 等. 电能计量设备自动检定流水线调度优化研究. 电测与仪表, 2015, 52(18): 41-45. DOI:10.3969/j.issn.1001-1390.2015.18.009 |
| [5] |
樊桦. 智能电能表国内外标准分析及开展全性能检测的可行性分析. 科技创新与应用, 2014(25): 13-14. |
| [6] |
吕宁, 熊智华, 王雄. 综合性SDG故障诊断架构. 计算机与应用化学, 2010, 27(1): 11-16. DOI:10.3969/j.issn.1001-4160.2010.01.002 |
| [7] |
姜洪权, 王金宇, 高建民, 等. 面向复杂系统故障溯源的SDG-FG模型建模方法. 计算机集成制造系统, 2015, 21(3): 749-757. |
| [8] |
张颖伟, 刘强, 张杨. 基于DKPLS的非线性过程故障检测. 华中科技大学学报(自然科学版), 2009, 37(SI): 58-61. |
| [9] |
邹永杰, 端木京顺, 高海龙. 基于核偏最小二乘的支持向量机回归算法研究. 计算机工程与设计, 2010, 31(10): 2290-2293. |
| [10] |
杨蕊. 基于定量知识的分层有向图故障诊断方法及其应用[硕士学位论文]. 太原: 太原理工大学, 2014.
|
| [11] |
杨恒占, 张可, 钱富才. 基于模糊分层SDG模型的故障推理方法. 计算机系统应用, 2017, 26(4): 104-109. DOI:10.15888/j.cnki.csa.005523 |
| [12] |
叶红. 可达矩阵的Warshall算法实现. 安徽大学学报(自然科学版), 2011, 35(4): 31-35. |
| [13] |
王平, 刘玉涛. 基于GA和LS-SVM的时间序列预测. 华北电力大学学报, 2009, 36(4): 100-103. |
| [14] |
王庆云, 黄道. 固定尺度最小二乘支持向量机. 华东理工大学学报(自然科学版), 2006, 32(7): 772-775. |
 2020, Vol. 29
2020, Vol. 29


