现实世界中的很多系统都可以被抽象为复杂网络, 如社交网络、技术网络、生物网络, 这些网络都具有一种普遍的特性——社区结构. 在不同类型的网络中, 社区有着不同的含义, 但是所有社区内部节点间的联系总是比不同社区节点间的联系密切, 准确地发现社区结构是在中观层面上理解复杂网络进而研究复杂系统的有效途径.

社区发现的研究历史可以追溯到1927年, Rice等基于投票模式的相似性发现小的政治团体中的社区^[1]. 早期的研究工作大部分都围绕非重叠社区发现展开, 此类算法将复杂网络划分成若干个互不相连的社区结构且一个节点只能隶属于一个社区^[2]. 然而, 现实中网络社区之间往往是相互重叠的, 硬划分的社区发现算法无法满足需求, 例如, 在社交网络中, 如果每个社区代表拥有共同兴趣爱好的用户所组成的群体, 则一个用户可以拥有诸多兴趣爱好而隶属于多个社区, 显然, 重叠的社区结构更能体现出复杂网络的特性, 进而帮助我们从中观层面对复杂系统进行分析.

对复杂网络中重叠社区的发现与研究也因此成为近年来新的研究热点, 而社区发现作为社区分析相关工作的前提, 对于其他领域的研究有着重要影响. 目前, 重叠社区的发现结果可以被应用于情感分析、个性化推荐、实体消歧和链接预测等领域的研究.

1 相关工作

近年来, 学者们相继提出大量能够识别重叠社区的算法. Palla等提出一种基于最大团的派系过滤算法CPM来分析重叠的社区结构^[3], 该算法易受k值影响, 且以最大团为种子的方式计算复杂度较高. COPRA算法^[4]对基于标签传播的非重叠社区发现算法进行改进, 在标签后面附上节点对该标签的归属系数, 以便衡量该节点包含多个社区的信息比重, 在迭代更新节点标签的过程中允许一个节点同时拥有多个标签, 以发现网络中的重叠社区, 该算法每次迭代的时间复杂度接近线性但稳定度较差. 基于链路的重叠社区发现算法首先对网络的边进行聚类, 然后通过收集链路社区内的所有连接的节点进行社区划分, 代表算法为LINK算法^[5]. 在此基础上, Li等^[6]提出一种基因表示模型, 通过将链路社区映射成节点社区的方式, 实现对重叠节点的发现. 基于局部社区优化和扩展的方法则从局部社区出发, 基于优化函数进行扩张, 社区间的交叉部分则为重叠节点, 代表算法为LFM算法^[7], 除此之外, Su等^[8]提出利用随机游走策略扩展优化的方法. 文献[9]在此基础上提出基于种子节点选择的重叠社区发现算法, 首先通过定义的影响力函数选取种子节点, 然后通过吸引力函数以种子节点为核心进行扩展, 发现种子所在的局部社区结构. 其中, 基于种子节点选择和扩展的算法由于稳定性好、效率高而成为主流的社区发现算法. Wang等^[10]提出一种基于结构中心性的种子选择算法, 实现了一个高覆盖率的朴实算法, 提高了社区发现质量, 但算法不能很好地适用于大规模数据集. 於志勇等提出的i-SEOCD算法能够高效地从种子节点出发进行局部扩展, 最终发现稳定的重叠社区^[11], 但是该算法在计算节点相似度时只考虑了局部网络, 提高算法执行效率的同时也牺牲了算法准确性.

现有基于种子节点扩展的重叠社区发现算法虽然在稳定性方面表现较好, 但在衡量两节点间关系时, 往往将两节点间是否有连边作为唯一判别标准, 而只考虑狭小作用域范围内的局部信息的做法, 虽然提升了社区发现的效率, 但忽略了网络中更大范围内节点和边因素对社区发现过程的影响, 使得算法在提升效率的同时往往以牺牲部分准确性为代价. 同时, 现有算法在基于种子节点进行社区扩展的过程中, 往往需要不断地迭代计算现有社区与未划分节点间的相似性关系, 计算量大, 不适合进行大规模网络的社区发现.

为了更好地解决以上问题, 本文利用Node2Vec^[12]算法对网络结构进行学习, 通过控制在游走产生节点序列过程中对深度优先和广度优先的趋向, 将更大范围内的拓扑结构信息体现到节点因素中, 提出了基于Node2Vec的重叠社区发现算法, 该算法能够解决现有算法存在的以牺牲准确性来提高效率和不适合大规模数据集的问题.

2 基于Node2Vec的重叠社区发现算法

针对以Jaccard相似度为指标衡量节点间距离的方法所存在的局限性, 本文采用网络表示学习算法学习到网络中每个节点的向量表示, 针对传统种子节点选择方法稳定性和鲁棒性差的缺点, 提出了新的种子节点选择算法, 并以此为基础进行社区扩张和优化.

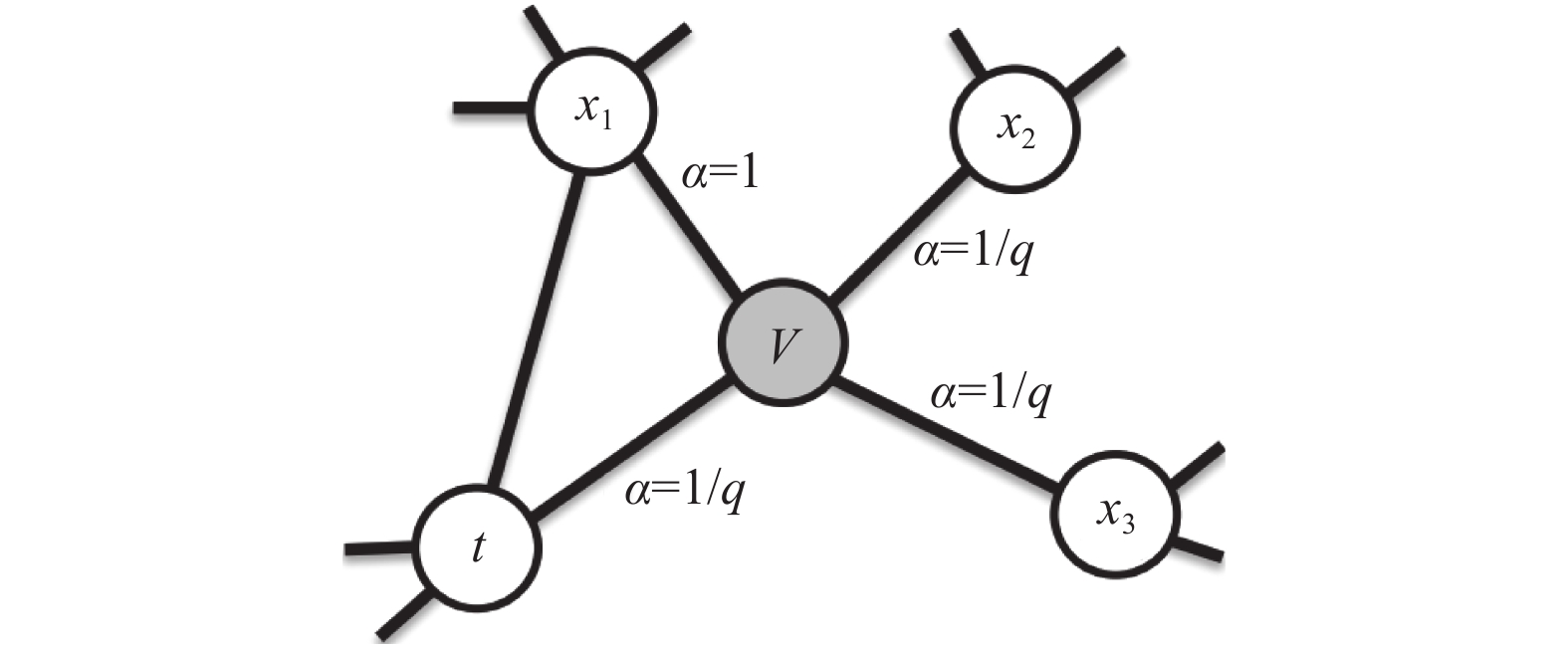
2.1 Node2Vec算法

Perozzi等^[13]提出了将Word2Vec的思想用于图节点表示学习的Deepwalk算法, Node2Vec在此的基础上改变了随机游走的序列生成方式, 通过半监督的方式学习p, q两个超参数的值, 控制游走对深度和广度的趋向, 其中p控制跳向前节点邻居的概率, q控制跳向前节点非邻居的概率, 如图1所示.

图1中, $q > 1$ 时, 趋向于遍历临近t节点的 ${x_1}$ 节点, 即趋向于BFS; $p > 1$ 时, 趋向于遍历临近t节点的 ${x_2}$ 或 ${x_3}$ 节点, 即趋向于DFS. 在确定要遍历的邻居节点之后, 采用skip-gram模型进行训练进而获得节点的向量表示.

在进行种子节点发现前, 首先利用Node2Vec算法对网络结构进行学习, 在学习到网络中每个节点的向量表示后, 对于任意节点 $u$ 和 $v$ , 可利用算法内置的相似度计算工具计算其在高维空间中的相似度 $sim(u,v)$ , 其取值范围为0~1, 通过该方式进一步计算网络中任意节点之间的相似度, 并用相似度矩阵 ${A_{{{n}} \times {{n}}}}$ 表示整个网络中节点间的相似度信息, 其中 ${A_{uv}}$ 表示节点 $u$ 和 $v$ 之间的相似度, 进而可以用 $1 - sim(u,v)$ 来表示节点间的相异度.

2.2 种子节点选择算法

通常, 一个网络可以用无向图 $G = (V,E)$ 表示, 其中V表示图中n个节点的集合, E表示图中m条边的集合.

在网络中, 节点u的邻居集合N(u)定义如下:

$N(u) = \{ u:v \in V,(u,v) \in E\} \;$

(1)

节点u对节点v的影响力用F(u,v)表示如下:

$F(u,v) = \frac{{D(u)D(v)}}{{{{(1 - sim(u,v))}^2}}}$

(2)

其中, D(u)和D(v)分别表示节点u和v的度, $sim(u,v)$ 表示u, v节点的相似度, 可通过Node2Vec生成的节点向量计算得到, $1 - sim(u,v)$ 表示为两节点间的距离, 距离越远, u对v的影响力越小.

节点u的影响力值通过以下公式计算得到:

$F(u) = \sum\limits_{v \in N(u)} {\frac{{D(u)D(v)}}{{{{(1 - sim(u,v))}^2}}}} $

(3)

节点影响力的大小与其邻居节点的数量、度数以及相异度有关, 影响力越大, 节点越有机会成为种子节点.

在种子节点选择算法中, 首先根据节点的向量计算所有节点的影响力值, 如果某节点的影响力值比其所有邻居节点的影响力值都大, 则将该节点加入到种子节点的集合中. 算法1中列出了种子节点选择算法的伪代码, 其中2–4行利用定义的节点影响力计算公式计算出每个几点的影响力值, 5–9行将每个节点的影响力值与其所有邻居的影响力值进行比较, 若邻居节点中没有比当前节点影响力值大的节点, 则将该节点加入到种子节点集合中.

算法1. 种子节点选择算法

输入: 无向图 $\scriptstyle G = (V,E)$ ; 相似度矩阵 $\scriptstyle{A_{{{n}} \times {{n}}}}$ .

输出: 种子节点集合S.

1. $\scriptstyle S \leftarrow \emptyset $

2. for $\scriptstyle u \in V$ do

3.　利用式(3)计算F(u)

4. end for

5. for u $\scriptstyle \in $ V do

6.　if $\scriptstyle \forall v \in N(u)$ and $\scriptstyle F(u) \ge F(v)$

7.　　 $\scriptstyle S \leftarrow S \cup u$

8.　end if

9. end for

10. return S

2.3 社区扩展算法

针对现有算法在社区扩张过程中重复计算量大的问题, 本文在得到分布均匀、影响力大的种子节点之后, 充分利用前一阶段计算所得的节点相似度矩阵, 从每个种子节点出发进行社区扩展, 首先, 以集合中的每个种子节点为核心构建社区, 若节点与种子节点的相似度大于阈值 $\varepsilon $ , 则将该节点划入该种子节点所属的社区, 然后, 对于尚未被划分的节点, 比较其与各个种子节点的相似度, 选取与之最相似的种子节点, 加入其所在社区, 最终完成社区的划分.

算法2中列出了社区扩展算法的伪代码, 2–4行首先将所有节点标记为false, 5–13行分别以每个种子节点为核心进行社区扩展, 并将被划分的节点标记为true, 此过程中以各节点为核心的社区独立进行扩展, 能够很好地根据阈值 $\varepsilon $ 的大小控制重叠节点的规模, 阈值 $\varepsilon $ 越小, 发现重叠节点的几率越大, 14–19行将一轮划分结束后没有归属的节点分离出来, 20–25行则对标记为false的节点进行处理, 选择与之相似度最高的种子节点所在的社区作为其社区归属, 最终经过两个阶段的处理, 得到最终的社区.

算法2. 社区扩展算法

输入: 无向图 $\scriptstyle G = (V,E)$ ; 相似度矩阵 $\scriptstyle{A_{{{n}} \times {{n}}}}$ ; 种子集合S.

输出: 社区结构C.

1. $\scriptstyle C \leftarrow \emptyset $

2. for $\scriptstyle u \in V$ do

3.　 $\scriptstyle Label(u) = {\rm false}$

4. end for

5. for seed in S do

6.　 $\scriptstyle CS \leftarrow \emptyset ,CS \leftarrow CS \cup \{ seed\} $

7.　for $\scriptstyle u \in V$ and $\scriptstyle u \notin S$

8.　　if $\scriptstyle A[seed][u] \ge \varepsilon $

9.　　　 $\scriptstyle CS \leftarrow CS \cup \{ U\} $ , $\scriptstyle Label(u) = {\rm true}$

10.　　end if

11.　end for

12.　 $\scriptstyle C \leftarrow C \cup CS$

13. end for

14. $\scriptstyle R \leftarrow \emptyset $

15. for node in V

16.　if $\scriptstyle Label(node) ={ \rm false}$

17.　　 $\scriptstyle R \leftarrow R \cup \{ node\} $

18.　end if

19. end for

20. for v in $\scriptstyle R$

21.　for seed in S

22.　　 CS_num = argmax $\scriptstyle A[seed][v]$

23.　end for

24.　 $\scriptstyle CS \leftarrow CS \cup \{ v\} $ , $\scriptstyle Label(v) = {\rm true}$

2.5 end for

26. return C

通常情况下, 选择合适的阈值 $\varepsilon $ 能够使得大部分节点经过第一阶段的处理能够划入相应的社区, 阈值 $\varepsilon $ 越小, 需要进行第二阶段处理的节点越少, 但也会导致社区之间重叠度很高. 本文在基于种子节点进行社区扩展的过程中, 充分利用前阶段的计算结果, 将迭代更新的过程简化成了寻址过程, 完美状态下, 只需进行 $k \times n$ 次计算即可完成社区检测, 最坏情况下, 则需进行 $2 \times k \times n$ 次计算, 其中 $k$ 表示种子节点个数, $n$ 表示网络中节点的个数, 且二者间满足 $k < < n$ , 总体复杂度为 $O(n)$ , 优于现有的时间复杂度为 $O(n\log n)$ 的社区扩展算法.

综上, 基于Node2Vec的重叠社区发现算法整体流程大致分为以下3个步骤:

首先, 利用NodeVec算法对网络结构进行学习, 得到包含丰富拓扑结构信息的节点的向量表示, 基于节点向量值计算每对节点间的相似度, 用一个 $n \times n$ 阶矩阵来表示网络结构中所有n个节点间的相似度值.

然后, 利用前一阶段计算得到的节点相似度, 根据定义的节点影响力公式筛选出能够独立领导社区的种子节点集合.

最后, 以种子节点为核心, 分阶段进行社区扩展, 首先通过比较每个种子节点与所有非种子节点间相似度与给定阈值的大小关系初步扩展社区, 然后对于未被划分的节点, 选择与之相似度最大的种子节点, 划入其所属社区, 直至所有节点都有至少一个社区归属, 重叠社区检测完毕.

3 实验

为验证算法的相关性能, 在多个不同规模的真实数据集上与其他经典重叠社区发现算法进行对比实验, 待比较的算法分别是CPM、LINK、COPRA和LFM算法.

3.1 实验数据集

分别选取不同类型不同数量级的5个真实网络数据集, 具体包括美国空手道俱乐部网络Karate^[14]、海豚关系网Dolphins^[15]、大学生足球联赛网络Football^[16]、欧洲研究机构电子邮件网络Email-EU^[17]和高能物理范畴论文引用关系网Ca-HepPh^[18], 各网络规模如表1.

3.2 评价指标

由于社区划分没有标准的结果, 对于真实数据集, Newman提出的模块度函数^[19]被广泛认可, 但该评价标准并不能很好地适用于重叠社区, Shen等在此基础上提出了能衡量重叠社区划分结果的重叠模块度函数^[20], 定义如下:

$EQ = \frac{1}{{2{{m}}}}\sum\limits_i {\sum\limits_{u \in {c_i},v \in {c_i}} {\frac{1}{{{Q_u}{Q_v}}}} } \left[{A_{uv}} - \frac{{{k_u}{k_v}}}{{2m}}\right]$

(4)

其中, $m$ 表示网络中的总边数, $A$ 为网络的邻接矩阵, ${k_u}$ 为节点 $u$ 的度数, ${Q_u}$ 表示节点 $u$ 所属的社区数量.

3.3 实验结果

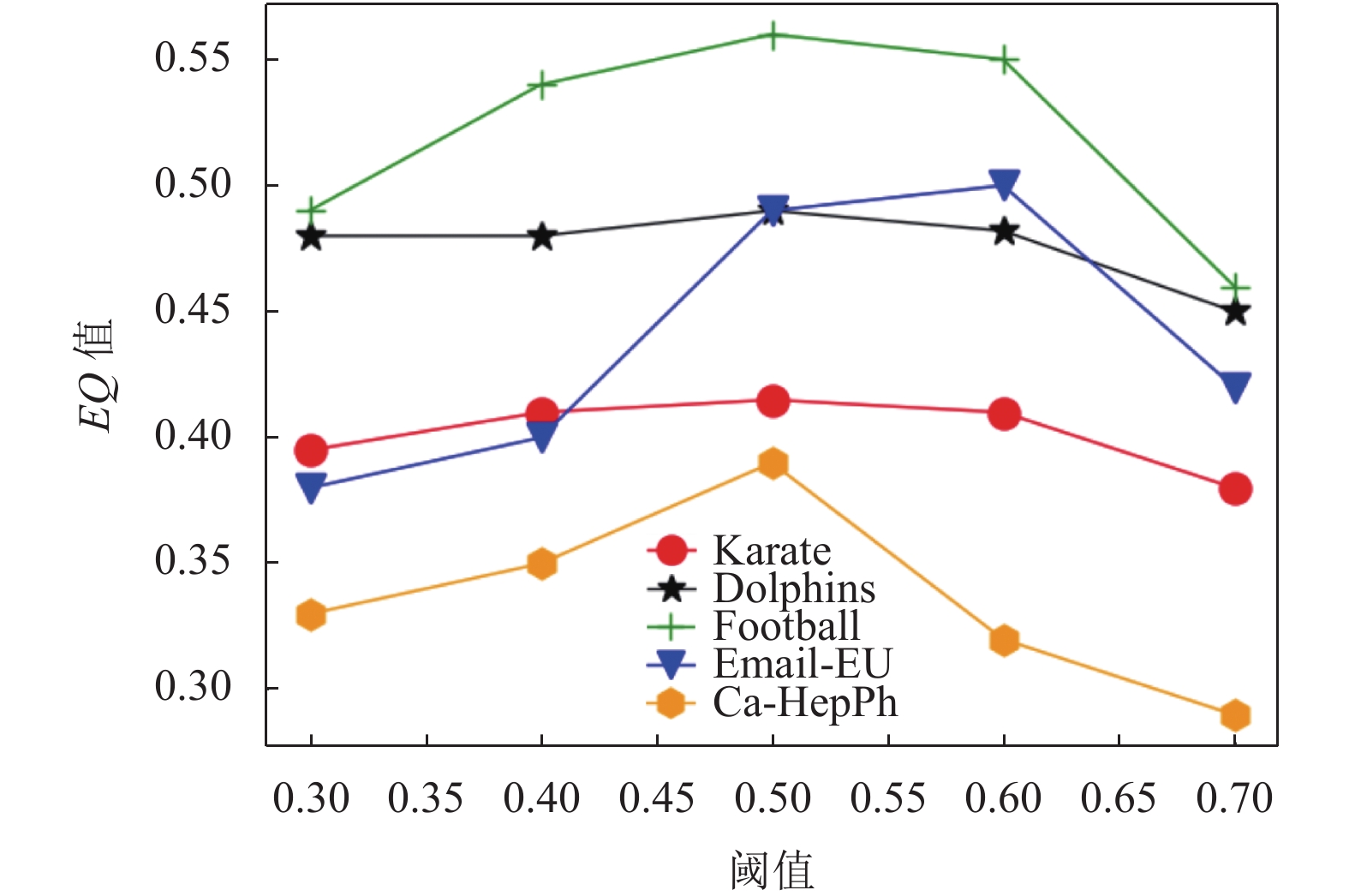
本文提出的算法在基于种子节点进行社区扩展时, 社区划分结果易受阈值 $\varepsilon $ 大小的影响, 故首先在不同数据集上在不同阈值 $\varepsilon $ 的指引下进行社区划分, 通常情况下阈值 $\varepsilon $ 的取值范围为0.3~0.7, 取步长 $h = 0.1$ 进行实验, 社区划分结果随阈值 $\varepsilon $ 大小改变而变化的情况如图2

从图2可以看出, 在不同数据集上, 模块度总是在 $\varepsilon = 0.5$ 左右的位置取到峰值, 这也说明阈值 $\varepsilon $ 对划分结果的影响趋势在所有数据值上是大致相当的.

将本文算法与其他4个经典的重叠社区发现算法在不同规模不同类型的数据集上进行对比实验(阈值取 $\varepsilon = 0.5$ ), 结果如表2所示.

在大多数数据集上, 本文算法均取得了最高的模块度值, 尤其是在Emai-EU和Ca-HepPh两个大规模的数据集上, 分别取得了接近0.5和0.4重叠模块度值, 所发现的社区质量明显优于其他算法, 实验证明, 使用Node2Vec算法将更大作用域范围内的网络信息映射到节点向量中的方式, 能够有效地避免范围限制所带来的准确率方面的牺牲, 提升社区发现质量, 在规模大、结构复杂的网络上, 提升效果格外显著.

4 结论与展望

本文提出了一种基于Node2Vec的重叠社区发现算法, 首先获得网络结构的向量表示并计算节点之间的相似度值, 利用定义的影响力函数选择出种子节点, 然后以每个种子节点为核心进行社区扩张. 本文选取了不同类型不同规模的真实网络数据集, 并在这些数据集上将本文算法与其他类经典重叠社区发现算法进行对比性实验, 实验结果表明, 本文算法在大部分数据集尤其是大规模数据集上表现出了明显的优势. 后续工作将提高算法的性能, 降低算法复杂度, 并将算法应用到动态社区发现研究中.