2. 武汉科技大学 冶金自动化与检测技术教育部工程研究中心, 武汉 430081
2. Engineering Research Center for Metallurgical Automation and Measurement Technology of Ministry of Education, Wuhan University of Science and Technology, Wuhan 430081, China
视觉跟踪技术作为计算机视觉的热门研究课题之一, 被广泛应用于智能视频监控、精确制导、医疗诊断、智能交通系统、人机交互等领域. 在视觉跟踪中除了会出现运动模糊、尺度变换和平面外旋转等情况外, 因受到活动范围的限制, 出现静态或动态障碍物而使目标被长期完全遮挡, 使目标消失在可测视线中. 跟踪中的遮挡处理是难点之一. 目前, 国内外研究者已为解决跟踪中的遮挡问题进行了大量的研究, 其中经典方法有Mean-shift算法、基于子块匹配的算法、Kalman滤波算法和粒子滤波算法等, 还有基于时空上下文的方法及目前比较常用的相关滤波类方法. 经典的跟踪方法处理遮挡, 例如李菊等[1]通过K均值聚类算法对空间特征与权重分布近似的粒子聚类, 能解决目标局部遮挡问题. 周越等[2]利用结合Kalman滤波预测机制以改进Mean-shift算法, 能减少迭代次数, 提高跟踪稳定性. 张红颖等[3]通过将目标整体颜色特征划分为几块局部颜色特征, 来提高Mean-shift跟踪算法抗遮挡性. 但是这些方法对背景的利用率低, 面临着目标在不同情形下对表观模型的拟合难题. 梁宵等[4]利用基于时空上下文的方法处理遮挡, 存在着特征单一和学习率固定的不足. 相关滤波类方法处理遮挡, 例如赵径通等[5]通过用零均值归一化的互相关系数作为判别遮挡的条件能有效处理部分遮挡. 闫河等[6]通过在核相关滤波的训练阶段将目标的HOG和LBP特征融合解决遮挡. 然这些方法局限于目标位置预测, 对跟踪中的尺度变化还无法有效处理.
判别尺度空间跟踪算法DSST[7]是一种将位置滤波器和尺度滤波器联合使用, 再分别对目标定位与尺度估计的特殊相关滤波类方法, 可以很好地解决跟踪中的尺度变化和遮挡问题, 精度上获得了2014年的VOT冠军. 因此在移动机器人[8]、智能监控[9]和智能驾驶[10]等领域应用很广. 但是需注意的是, DSST主要是解决短时间内的视频跟踪问题, 对于长时间遮挡下的跟踪易出现目标丢失现象.
为解决行人跟踪过程中由于目标处于长时间完全遮挡下, 背景对滤波器模型产生的影响, 而造成跟踪目标丢失的问题, 本文提出了一种改进的DSST行人遮挡跟踪的方法, 在DSST跟踪框架下, 先利用简单可靠的高置信度跟踪指标Fmax和APCE[11]作为行人被遮挡的依据, 再利用对形变具有强鲁棒性的可形变部件模型(DPM)[12]对行人重新定位. 该方法能解决目标因长时间被遮挡, 使模型被污染而引发跟踪丢失的问题, 且跟踪适应性好.
1 判别尺度空间跟踪算法判别尺度空间跟踪(DSST)是一种在视觉跟踪中精准的尺度估计方法. 首先通过多维特征的判别相关滤波器估计目标的位置, 再增加尺度滤波器估计目标的尺度信息. 位置滤波器和尺度滤波器相互独立.
首先提取目标所在图像块的多维特征f, 通过式(1)构造最优滤波器.
| $ \varepsilon = {\left\| {\sum\limits_{l = 1}^d {{h^l} \otimes {f^l} - g} } \right\|^2} + \lambda \sum\limits_{l = 1}^d {{{\left\| {{h^l}} \right\|}^2}} $ | (1) |
式中, f l、hl和g均为M×N的矩阵, l表示特征维度, l∈{1, ···, d}, λ为正则项系数,
| $ {H^l} = \overline G {F^l}\Bigg/\left( {\sum\limits_{k = 1}^d {\overline {{F^k}} {F^k} + \lambda } } \right) $ | (2) |
其中, 特征维数取值范围k∈{1, ···, d}, 最后利用式(3)进行迭代更新, 其中, η表示学习率.
| $\left\{ \begin{split} & A_t^l = \left( {1 - \eta } \right)A_{t - 1}^l + \eta \overline {{G_t}} F_t^l \\ & {B_t} = \left( {1 - \eta } \right){B_{t - 1}} + \eta \sum\limits_{k = 1}^d {\overline {F_t^k} } F_t^k \\ \end{split} \right. $ | (3) |
最后提取新一帧的图片块特征z, 求取每一维特征的二维DFT得到Zl, 利用式(4)算得响应g, g中最大值所对应的位置即是当前帧的目标位置.
| $y = {{\cal F}^{ - 1}}\left\{ {\sum\limits_{l = 1}^d {\overline {{A^l}} {Z^l}} /\left( {B + \lambda } \right)} \right\}$ | (4) |
为确定视频帧中运动目标的最佳尺度大小. 通过将当前帧的目标大小设为P×R, 尺度设为S, 在目标中心位置提取尺度等级为n的训练样本f作为Jn的d维的特征描述子, 其中获取大小为anP×anR, 窗口标记为Jn, a表示一个尺度因子, 尺度等级n选择原则为n∈{[–(S–1)/2], …, [(S–1)/2]}.
图1为多尺度相关响应过程, f以上帧目标位置为中心获取的不同尺度图像块的特征, h为滤波器模型, g为通过三维高斯函数得到的相应输出. 将特征f和响应输出g作为已知条件, 利用式(3)对模板h进行更新. 在新一帧的待检测图像中, 利用获取S个尺度上特征组成一个M×N×S的特征金字塔, 接着利用式(4)得到响应g, 最大响应值对应的位置和尺度即为目标位置和尺度信息.
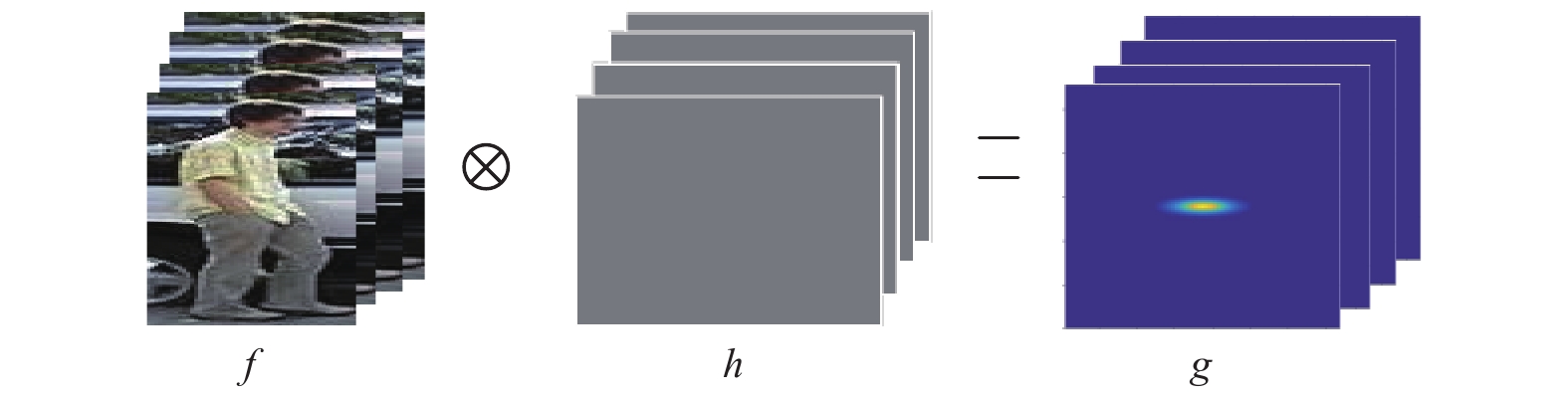
|
图 1 多尺度相关滤波响应过程 |
2 基于改进的DSST行人遮挡跟踪算法
针对DSST跟踪算法在目标被长期完全遮挡时, 在线学习过程中滤波器出现退化, 致使后续帧中出现跟踪丢失的现象. 为解决该问题, 提出了一种改进的DSST行人遮挡跟踪算法, 首先通过引入一种基于历史均值的跟踪遮挡检测策略, 判断目标是否出现遮挡, 若存在遮挡, 再利用基于DPM行人检测方法重新定位目标, 最后利用DSST稳健跟踪.
2.1 行人跟踪遮挡检测策略DSST算法不具有对检测结果可靠性判定的功能. 在跟踪过程中目标出现严重遮挡或完全遮挡时, 导致检测到的目标不准确, 引入一种基于最大响应值和平均峰值相关能量的历史均值的模型更新策略. 最大响应分数值计算方法如下:
| $ {F_{\max }} = \max F\left( {s, y; w} \right) $ | (5) |
式中, s为基于上一帧目标位置的图像块, y为目标位置, w为分类器参数, F是衡量(s, y)为目标的可能性函数通常Fmax值越大, 跟踪精度越高, 如式(5).
第二个置信度指标是平均峰值相关能量, 反应响应图的震荡程度和尖锐程度, 式(6)计算方式如下:
| $ APCE = \frac{{{{\left| {{F_{\max }} - {F_{\min }}} \right|}^2}}}{{mean\left( {\displaystyle\sum\limits_{w, h} {{{\left( {{F_{w, h}} - {F_{\min }}} \right)}^2}} } \right)}} $ | (6) |
其中, Fmax、Fmin和Fw, h分别表示最高响应、最低响应值及在(w, h)位置上的响应值. 通过判断当前帧的Fmax和APCE结果小于设定比例阈值β1, β2倍的历史平均值时, 则视为有遮挡, 并用所提方法重新定位目标, 可以防止目标模型被污染, 提升跟踪的准确性.
2.2 行人跟踪重定位先利用基于Fmax和APCE的历史均值计算策略判定行人是否有遮挡, 高置信度则认为无遮挡, 利用式(3)对跟踪模型迭代更新. 低置信度则认为有遮挡, 那么在后续跟踪中更新滤波器模型则会被污染, 造成跟踪目标丢失, 利用事先训练好的DPM行人模型与后续帧的图像进行匹配, 对目标重新定位. 具体方法为: (1)采用滑动窗口方法获取图像块; (2)对待检测的图片提取每个子图像块的改进HOG特征金字塔; (3)最后利用训练好的模型求每个子图像的得分, 得分最高的图像块确定为行人目标区域.
在行人跟踪中, 对于满足低置信度且无法检测到行人的后续帧, 则认为目标被完全遮挡或严重遮挡, 此时选择停止更新目标位置.
2.3 行人遮挡跟踪算法的流程本文跟踪算法主要有: (1)跟踪模块, 对给定的初始目标区域提取图像块多维特征f, 及使用高斯函数造响应g, 将f和g做DFT后代入式(2)得到滤波器模型, 接着在新一帧图像中提取图像块z, 每一维度特征做DFT后代入式(4)得到响应y, 响应y中最大值的所在位置即为目标位置和尺度.
(2) 重检测模块, 先通过行人跟踪丢失检测策略确定当前跟踪结果为低置信度, 再利用DPM重新定位目标, 再以该位置为中心获取图像块, 利用式(3)更新DSST滤波器模型. 图2为基于改进的DSST行人遮挡跟踪流程图.
3 实验结果与分析实验测试所用的数据是在线跟踪基准OTB数据集的视频子集, 在OTB的100个可用视频中选择了4个具有不同属性的视频, 分别为BlurBody、Human2、Human6和David3, 跟踪对象均为单个的行人, 以及自制了一个含有长时间完全遮挡属性的模拟实验视频MyData. 利用这些数据集将本文方法和DSST、KCF、LCT及CSK等有代表性的跟踪方法进行了比较.
3.1 实验的环境与参数使用Matlab进行实验仿真, 所用到的硬件部分是Intel(R)Core(TM)i5-3210MCPU, 主频2.50 GHz, 2 GB内存. 实验中, DSST算法的参数与文献[7]相同, 学习率η为0.025, 尺度因子a为1.02, 行人跟踪丢失检测策略部分, 两个系数β1, β2均取为0.3.
3.2 实验的性能评估方法实验中利用距离精度和成功率两种评估方法作为OTB数据集和自制视频数据的跟踪评价指标. 位置误差为所有视频帧的跟踪目标的中心位置与标准的目标的中心位置之间的欧几里得距离.
距离精确度即为满足中心位置误差小于阈值的所有帧数fpre占视频总帧数N的百分比.
| $Precision = \left[ {\left( {\sum\limits_{i = 1}^N {{f_{\rm pre}}} } \right)\Bigg/N} \right] \times 100\% $ | (7) |
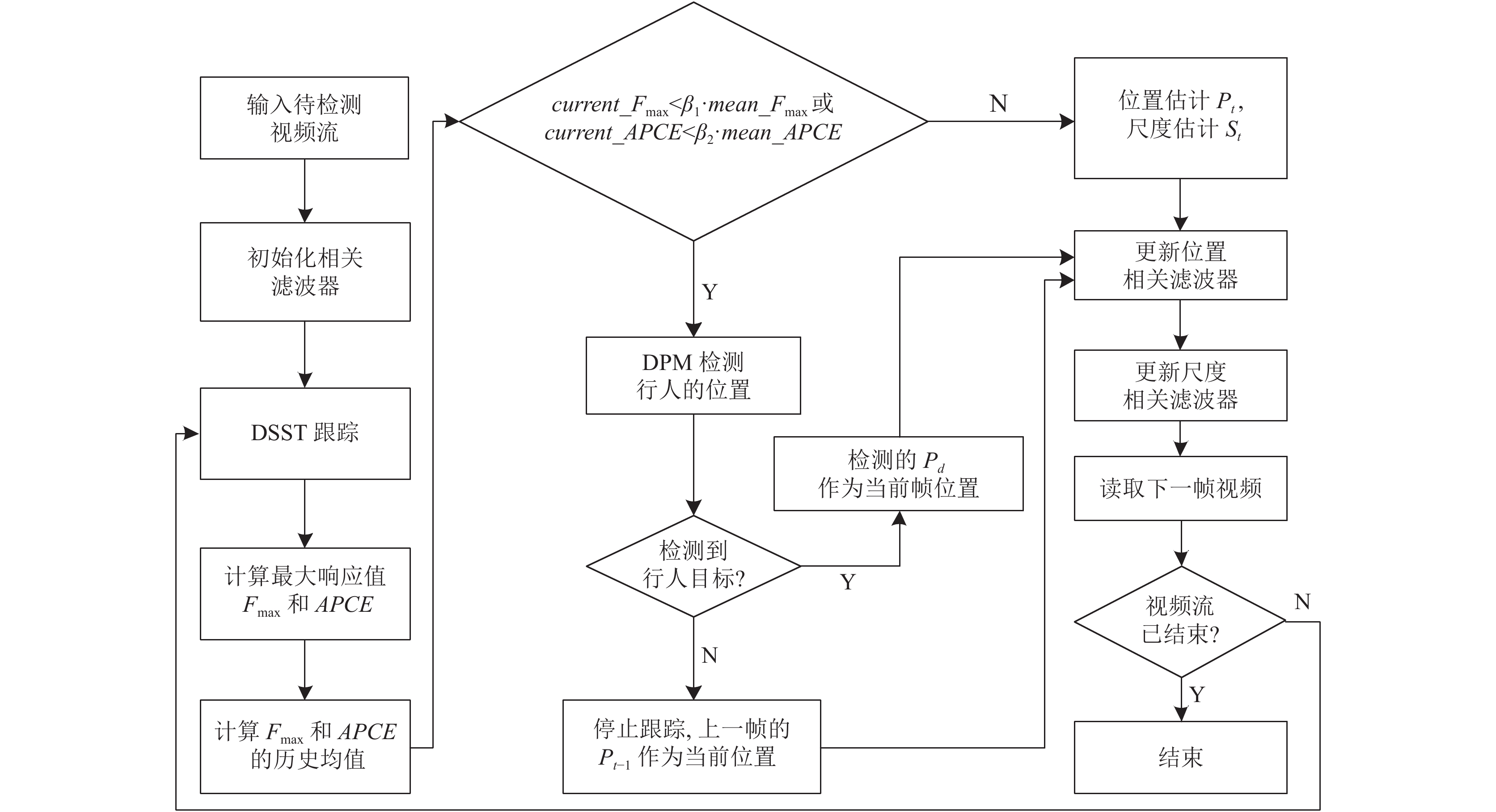
|
图 2 基于改进的DSST行人遮挡跟踪流程图 |
跟踪算法得到的目标区域面积表示为SRt, 标准目标区域面积表示为SRa, 重叠率定义为:
| $Overlap{\rm{ }}Rate = \frac{{\left| {{S_{Rt}} \cap {S_{Ra}}} \right|}}{{\left| {{S_{Rt}} \cup {S_{Ra}}} \right|}} $ | (8) |
其中,
| $success = \left[ {\left( {\sum\limits_{i = 1}^N {{f_{\rm suc}}} } \right)\Bigg/N} \right] \times 100{\text{%}} $ | (9) |
其中, 成功率的取值范围为0~1, 可绘制出一条曲线, 利用成功率曲线下面积(AUC)对跟踪效果的准确性进行评估, 及考虑到在快速运动下, 连续两帧之间真实目标框的中心位置的偏移大于20 pixels, 通过计算位置误差小于或等于20 pixels时的距离精度以及重叠率大于或等于0.5时的成功率, 评估跟踪效果准确性. 为了更好的反应本文方法的跟踪性能较其他算法的跟踪性能提升效果, 通过以某一种算法作为基准, 计算各算法获得精度相较于基准算法提升的比率. 将各算法获得的距离精度表示为PREtracker, 成功率表示为SUCtracker, 选择以LCT算法为基准, 基准算法获得距离精度表示为PREbase, 成功率表示为SUCbase, 计算方式如下:
| $Pr{o_{\rm PRE}} = \frac{{PR{E_{\rm tracker }} - PR{E_{\rm base}}}}{{PR{E_{\rm base}}}} \times 100\% $ | (12) |
| $Pr{o_{\rm SUC}} = \frac{{SU{C_{\rm tracker }} - SU{C_{\rm base}}}}{{SU{C_{\rm base}}}} \times 100\% $ | (13) |
其中, ProPRE表示为距离精度提升率, ProSUC表示为成功率提升率. 并且利用不同的线型曲线表示各算法在位置误差阈值选取范围为0到50 pixels内获得的距离精度曲线, 以及重叠率阈值选取范围为0到1内获得的成功率曲线, 获得的距离精度图横轴为位置误差阈值, 纵轴为距离精度, 成功率图横轴为重叠率阈值, 纵轴为成功率.
3.3 行人跟踪性能比较 3.3.1 整体性能比较在实验中为对跟踪算法性能进行评估, 使用了常规的评估方法, 一次性通过评估方法(OPE)对本文跟踪方法与其他4个跟踪算法进行性能比较, 该方法利用OTB数据集中标准的目标位置对视频第一帧初始化, 获得跟踪算法的距离精度和成功率.
图3为各算法在OPE评估下的距离精度图和成功率图, 由图3(a)和图3(b)的距离精度曲线及成功率图AUC可知, DDSST的跟踪精度优于选取的4种算法. 表1为各算法在测评数据集上的距离精度和成功率, 及其ProPRE和ProSUC. 由表1可知, DDSST算法获得的距离精度和成功率最高, 在ProPRE和ProSUC上, DDSST相比LCT分别提高了106%和124%. 相比DSST分别提高了14%和22%. 相比CSK分别提高了51%和59%. 相比KCF算法分别提高了75%和96%. 由分析知, 相比其它算法, DDSST整体跟踪性能更好.
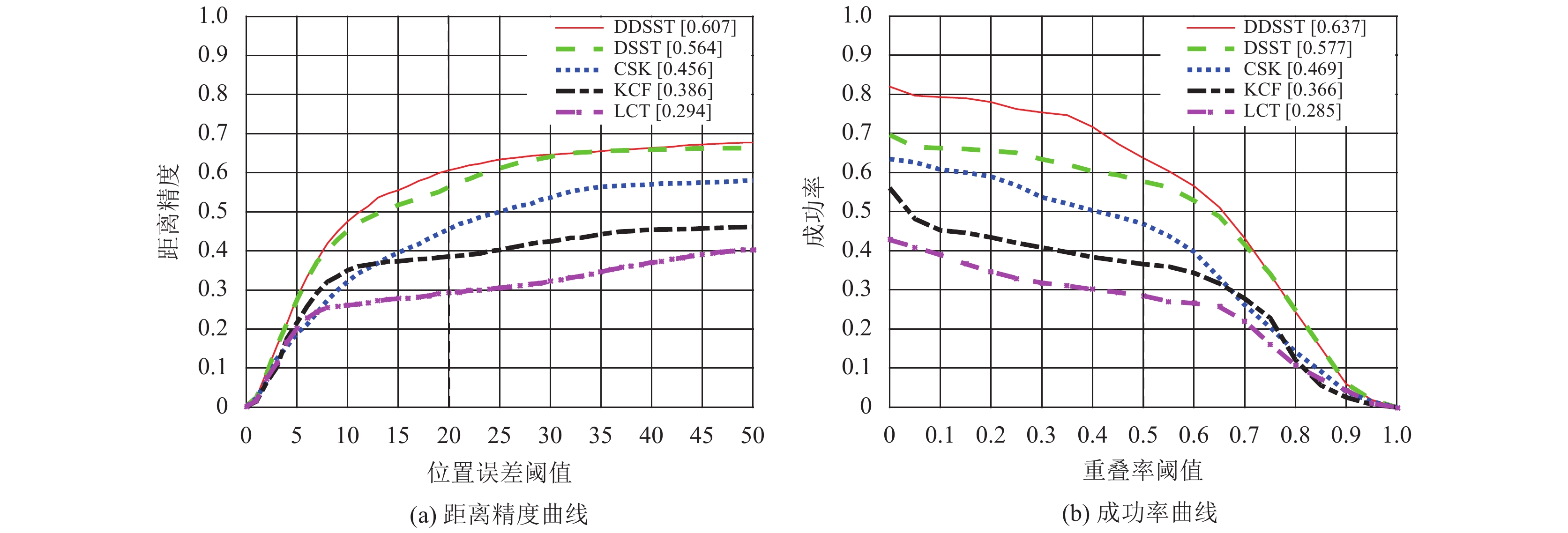
|
图 3 各算法在OPE评估下的距离精度和成功率 |
| 表 1 各算法在测评数据集上的距离精度和成功率(%) |
3.3.2 特殊属性下的行人跟踪性能比较
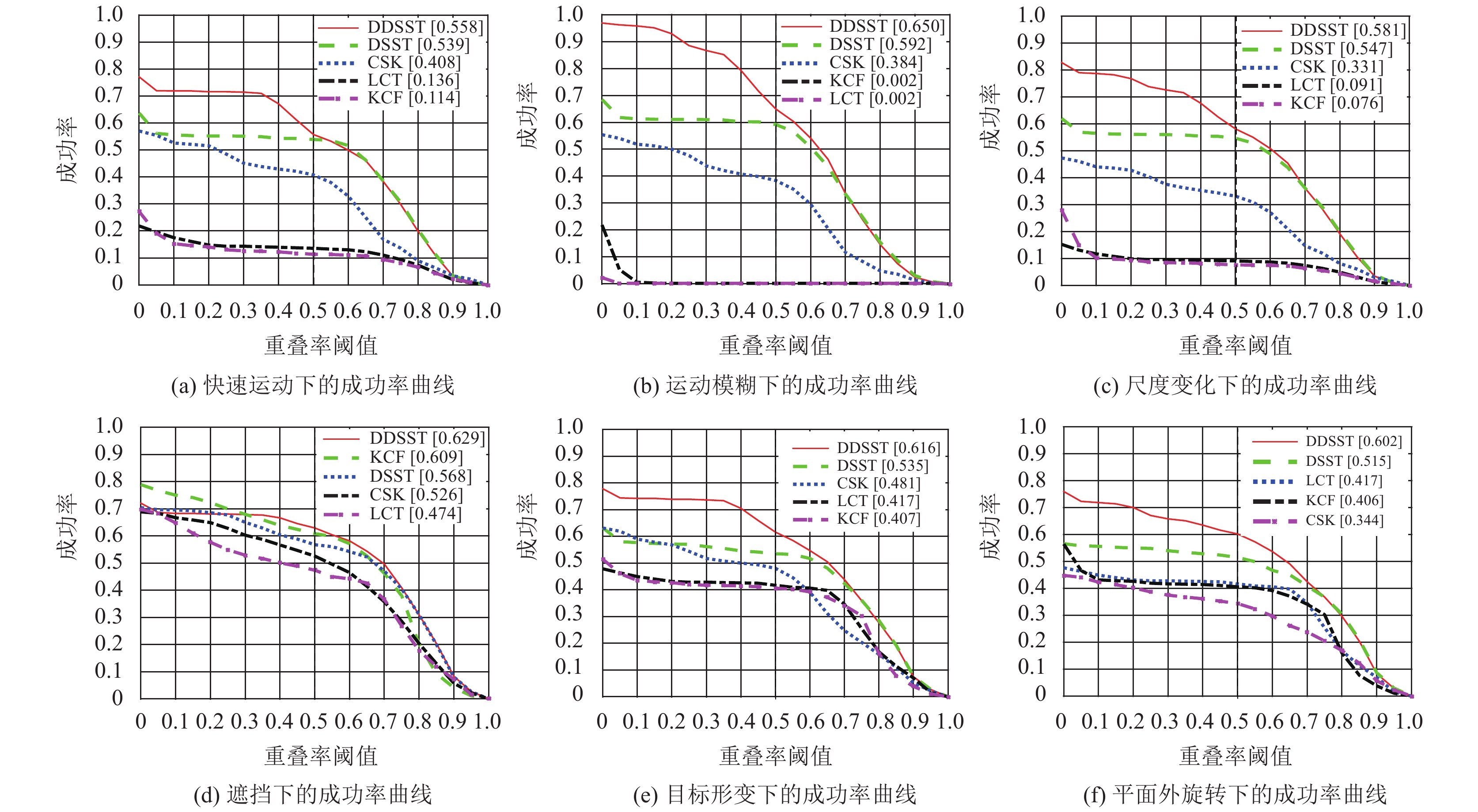
为了进行详细的分析, 对本文的5种算法在选取的6种不同属性下的跟踪性能进行评估. 图4和图5分别为各算法在6种属性下使用OPE评估方法测试获得的距离精度曲线图或成功率曲线图,
表2和表3分别为各算法在不同属性下获得的距离精度和成功率, 由表2和表3的第一列分别可知, 从上往下依次为快速运动(FM)、运动模糊(MB)、尺度变化(SV)、遮挡(OCC)、形变(DEF)和平面外旋转(OPR)等属性下获得的距离精度和成功率, 以及各算法的ProPRE和ProSUC.
由图4(d)、(e)和(f)知, 在遮挡、形变和平面外旋转等不同情况下位置误差阈值为20pixels时, DDSST获得的距离精度均为最高. 由图5(d)、(e)和(f)知, 在重叠率阈值范围为0.5到1内, 成功率AUC均为最大, 在阈值为0.5时成功率均为最高. 由表2和表3知在目标形变、平面外旋转和遮挡等不同情况下DDSST的距离精度分别为60.8%、56.3%和66.1%, 成功率分别为61.6%、60.2%和62.9%. 在ProPRE上, 比DSST分别提高了12%、20%和11%, 在ProSUC上, 比DSST分别提高了20%、20%和13%. 由分析知在目标形变及平面外旋转下本文方法相比DSST更准确且适应性好, 提高了抗遮挡性.
由图5(a)、(b)和(c)知, 在快速运动、运动模糊和尺度变化等不同情况下DDSST的成功率AUC均为最大, 重叠率阈值为0.5时DDSST的成功率最高, 由图4(b)和(c)知, 在位置误差为20 pixels时DDSST距离精度为最高, 由图4(a)知DDSST与DSST获得距离精度最为接近. 由表2和表3知, 在快速运动、运动模糊和尺度变换等不同情况下, DDSST的距离精度分别为51.9%、52.5%和49.8%, 成功率分别为55.8%、65.0%和58.1%, 在ProSUC上DDSST较DSST分别提高了14%、2900%和37%, 在快速运动下的ProPRE较DSST相差11%, 在运动模糊和尺度变换下的ProPRE比DSST分别提高了1350%和18%, 由分析知, 相比DSST, 本文方法在运动模糊下跟踪准确率提升很大, 且在尺度变换下保留了原DSST稳定性.
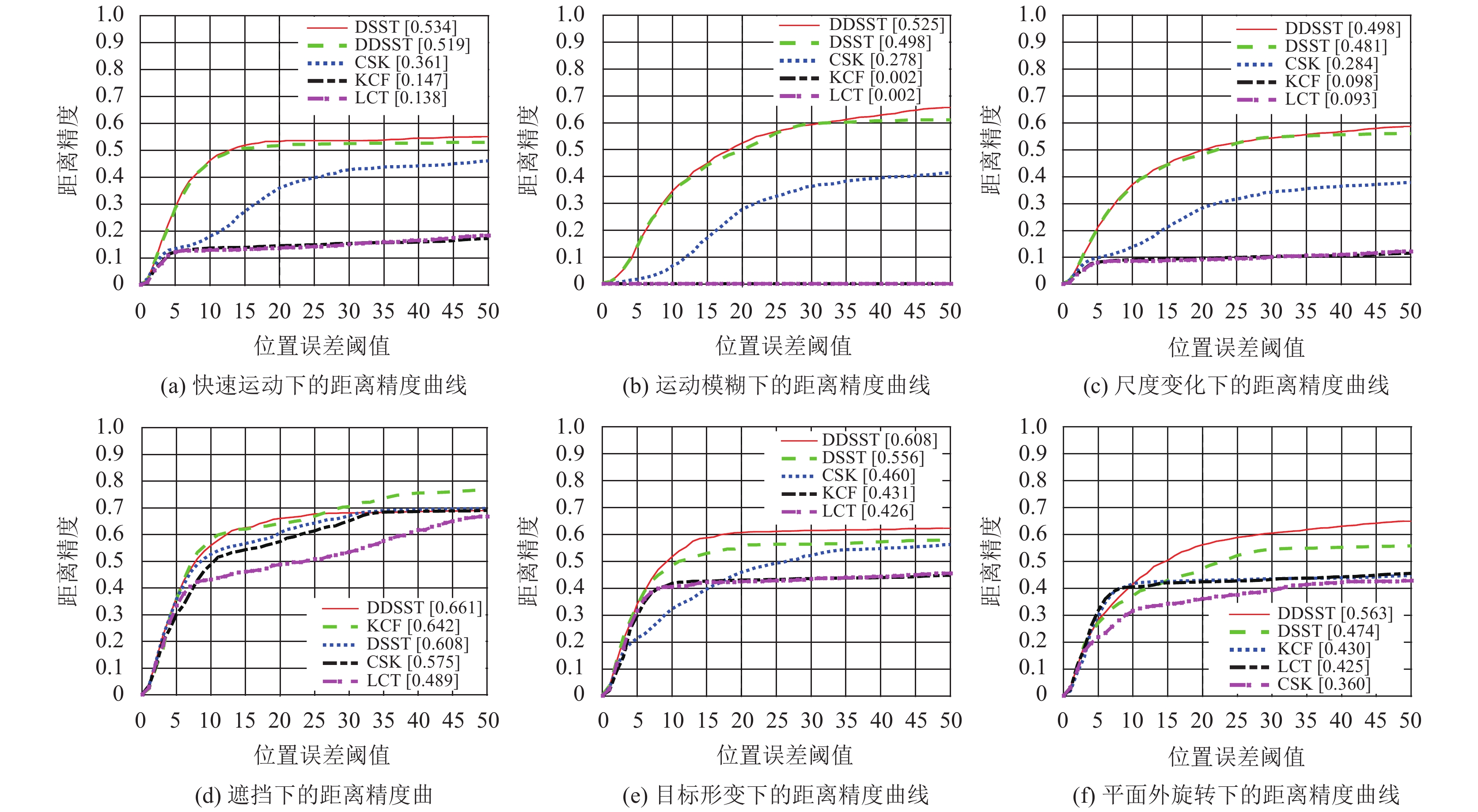
|
图 4 各算法在6种属性下的距离精度 |
|
图 5 各算法在6种属性下的成功率 |
| 表 2 各算法在6种属性下的距离精度(%) |
| 表 3 各算法在6种属性下的成功率(%) |
图6为各算法在测试的视频序列上跟踪效果对比图, 图6中的子图分别为在视频数据Human2、Human6、BlurBody、David3和MyData上的测试效果, 不同算法获得的跟踪效果用不同线型的矩形框进行表示, 如子图题标注.
(1) 各算法在遮挡下的实验效果比较
选取MyData和David3数据集中遮挡的跟踪情况, 由图6(e)第204帧和第283帧知目标处于长期完全遮挡, 由第355帧知, DDSST跟踪目标效果更好. 由图6(d)的第84帧知, 行人目标发生遮挡. 由第107帧知, 本文方法在发生短时遮挡后能有效跟踪行人.
(2) 各算法在尺度变化下的实验效果比较
选取Human6数据集中尺度变化下的跟踪情况, 从图6(b)的第87帧、第204帧、第224帧和第297帧, 目标发生显著的尺度变化, 由第297帧知, 只有DDSST和DSST能准确跟踪, 其他算法已失效.
(3) 各算法在平面外旋转下的实验效果比较
选取Human2和David3数据集中平面外旋转下跟踪情况, 由图6(a)的第106帧和第488帧知行人发生平面外旋转, 由第488帧知, 此刻只有DDSST和DSST能在平面外旋转下稳定跟踪目标. 由图6(d)的第107帧和第150帧知在目标发生平面外旋转下, 本文所选的各算法均能稳定跟踪.
(4) 各算法在目标形变下的实验效果比较
选取Human2数据集中目标形变属性下的跟踪情况, 由图5(a)的第488帧和第962帧知行人发生了形变, 由第962帧可知只有DDSST能有效跟踪.
(5) 各算法在运动模糊下的实验效果比较
选取Blurbody数据集中运动模糊属性下的跟踪情况, 由图6(c)的第14帧、第70帧和第110帧知, DDSST和DSST算法能有效跟踪目标.

|
图 6 各算法在测试的视频序列上跟踪效果对比图 |
4 结论
通过实验发现在利用DSST跟踪行人过程中当目标长时间受到大面积遮挡时, 继续使用DSST算法跟踪会导致后续帧中发生目标丢失的问题, 针对目标在长时间的遮挡和干扰下造成模型污染, 本文在采用DSST跟踪基础上, 引入高置信度更新机制对遮挡准确判断, 在目标可能发生遮挡时, 利用DPM检测当前帧的目标, 定位行人位置, 然后在该位置附近扣取图像块, 更新滤波器模型, 可重新跟踪到目标. 最后, 通过实验结果分析了改进算法与其他算法的跟踪性能, 在整体的数据集上所提方法的距离精度和成功率均为最高, 通过以LCT算法获得精度为基准, 改进的算法相比DSST算法分别提升了14%和22%. 在运动模糊、形变、遮挡、尺度变换和平面外旋转等6种不同情况下采用所提方法获得的距离精度和成功率同样均为最高, 相比DSST算法的跟踪效果更准确, 适应性更好. 在长时间完全遮挡的情况下, 使用改进的算法能解决跟踪目标丢失问题.
| [1] |
李菊, 曹明伟, 余烨, 等. 抗遮挡自适应的粒子滤波算法. 系统仿真学报, 2018, 30(9): 3552-3557. DOI:10.16182/j.issn1004731x.joss.201809041 |
| [2] |
周越, 宿佳钰, 蒋柯. 基于改进型的抗遮挡运动目标跟踪算法. 电子世界, 2019(22): 18-19, 22. DOI:10.19353/j.cnki.dzsj.2019.22.005 |
| [3] |
张红颖, 王赛男, 胡文博. 基于分块颜色直方图的MS跟踪算法. 中国民航大学学报, 2019, 37(1): 39-45. DOI:10.3969/j.issn.1674-5590.2019.01.008 |
| [4] |
梁宵, 沈茂先, 陈国栋. 一种抗遮挡的时空上下文目标跟踪. 火力与指挥控制, 2019, 44(6): 54-58, 63. DOI:10.3969/j.issn.1002-0640.2019.06.010 |
| [5] |
赵径通, 吴钟建, 李黎. 一种抗遮挡的相关滤波器跟踪算法. 科技经济导刊, 2015(18): 15-16, 43. |
| [6] |
闫河, 张杨, 杨晓龙, 等. 一种抗遮挡核相关滤波目标跟踪算法. 光电子·激光, 2018, 29(6): 647-652. DOI:10.16136/j.joel.2018.06.0286 |
| [7] |
Danelljan M, Häger G, Khan FS, et al. Accurate scale estimation for robust visual tracking. Proceedings of the 25th British Machine Vision Conference, BMVC 2014. Nottingham, UK. 2014. 1–7.
|
| [8] |
杜奇. 移动机器人的视觉目标跟踪方法研究与实现[硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2016.
|
| [9] |
扆梦楠, 白一帆, 邓红霞, 等. 变电站场景下高置信度策略的DSST目标检测及跟踪. 科学技术与工程, 2018, 18(23): 257-264. DOI:10.3969/j.issn.1671-1815.2018.23.036 |
| [10] |
曾鸽. 基于深度学习的驾驶员疲劳状态检测研究[硕士学位论文]. 长沙: 湖南大学, 2018.
|
| [11] |
Wang MM, Liu Y, Huang ZY. Large margin object tracking with circulant feature maps. Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, HI, USA. 2017. 4800–4808.
|
| [12] |
Felzenszwalb PF, Girshick RB, McAllester D, et al. Object detection with discriminatively trained part-based models. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(9): 1627–1645.
|
 2020, Vol. 29
2020, Vol. 29


