在信用贷款不断发展的今天, 信用评分已成为金融机构日益关注的问题, 目前已成为研究的热门问题. 信用评分是金融业的重要组成部分, 在信用客户选择、风险计量、贷款前后监管、综合绩效评估和资产组合风险管理等现代事务中发挥着重要作用[1]. 在银行、金融机构以及基于互联网的金融公司中, 强大的信用风险预测能力可以更好地巩固市场上的可持续利润. 信用评分的目的是将申请人分为两类: 信誉良好的人和信誉不良的人[2]. 信誉良好的人很有可能还清财务义务. 信誉不良的人极有可能发生违约. 信用评分的准确性对金融机构的盈利能力至关重要. 即使将信用不良的申请人的信用评分准确性提高1%, 也将减少金融机构的巨大损失.
针对信用评估的方法主要有逻辑回归[3]、支持向量机[4]、神经网络[5]和决策树[6]等. 传统的对信用评估的模型主要采用单一模型. 如王黎等[7]直接采用Gradient Boosted Decision Tree (GBDT)的方法对个人信用进行评估. 罗方科等[8]运用逻辑回归模型对小额贷款风险进行评估. 然而, 单一模型在处理非线性问题时效果并不十分理想.
为了解决单一模型的问题, 对模型进行组合应用逐渐成为提高信用评估准确率以及稳定性主要方法. Wang等[9]将逻辑回归分析、决策树、人工神经网络以及支持向量机多个分类器(即集成学习)结合使用, 显著提高单个基础学习者的学习能力. Koutanaei等[10]提出特征选择算法和集成学习分类器的混合数据挖掘模型引用于信用评估, 将4种特征选择算法进行比较得出PCA算法较好. He等[11]为信用评分生成一个新颖的集成模型, 使用粒子群优化算法进行基本分类器的参数优化, 减少了数据不平衡带来的负面影响, 提高了信用评分方面预测模型的综合性能. 刘潇雅等[12]应用C4.5信息熵增益率方法进行特征选择, 减少了数据的冗余属性. 王名豪等[13]对混沌粒子群法进行改进, 并应用于XGBoost算法中进行参数优化, 提高了信用评估的准确性.
基于上述研究进展, 本文提出基于改进的GS-XGBoost的个人信用评估研究, 用改进的网格搜索法寻找分类器的最优参数. 实验部分, 在UCI机器学习数据库中的信贷数据集上比较了本文提出GS-XGBoost与其他常用算法的性能. 实验结果表明, 本文算法具有较高的预测准确率, 是进行信用风险评估的有效模型.
1 理论与方法 1.1 XGBoost模型XGBoost (eXtreme Gradient Boosting)是极限梯度提升算法, 由Chen等[14]设计, 主要使提升树突破自身的计算极限, 来实现运算快速, 性能优秀的工程目标.
XGBoost的目标函数为:
| $\left\{\begin{split} & L = \displaystyle\sum\limits_i {l({{\hat y}_i},{y_i})} + \displaystyle\sum\limits_k {\Omega ({f_k})} \\ & \Omega (f) = \gamma T + \dfrac{1}{2}\lambda {\left\| w \right\|^2} \\ \end{split} \right.$ | (1) |
其中,
在XGBoost中, 完整的迭代决策树的公式应该写作:
| $\hat y_i^{(k + 1)} = \hat y_i^{(k)} + \eta {f_{k + 1}}({X_i})$ | (2) |
其中,
式(1)中的树集成模型L将函数
| $\begin{split} {L^{(t)}} =& \sum\limits_{i = 1}^n {l({y_i},} \hat y_i^{(t - 1)} + {f_t}({X_i})) + \Omega ({f_t}) \\ \approx & \sum\limits_{i = 1}^n {\left[ {{g_i}{f_t}({X_i}) + \frac{1}{2}{h_i}f_t^2({X_i})} \right]} + \Omega ({f_t}) \\ \end{split} $ | (3) |
其中,
定义
| $\begin{split} {L^{(t)}} =& \displaystyle\sum\limits_{i = 1}^n {\left[ {{g_i}{f_t}({X_i}) + \frac{1}{2}{h_i}f_t^2({X_i})} \right]} + \gamma T + \frac{1}{2}\lambda \displaystyle\sum\limits_{j = 1}^T {w_j^2} \\ =& \displaystyle\sum\limits_{j = 1}^T {\left[ {\left(\displaystyle\sum\limits_{i \in {I_j}} {{g_i}} \right){w_j} + \frac{1}{2}\left(\displaystyle\sum\limits_{i \in {I_j}} {{h_i}} + \lambda \right)w_j^2} \right]} + \gamma T \\ \end{split} $ | (4) |
对于固定结构
| $w_j^* = - \dfrac{{\displaystyle\sum\limits_{i \in {I_j}} {{g_i}} }}{{\displaystyle\sum\limits_{i \in {I_j}} {{h_i} + \lambda } }}$ | (5) |
| ${L^{(t)}}(q) = - \dfrac{1}{2}\displaystyle\sum\limits_{j = 1}^T {\dfrac{{{{\left(\displaystyle\sum\limits_{i \in {I_j}} {{g_i}} \right)}^2}}}{{\displaystyle\sum\limits_{i \in {I_j}} {{h_i} + \lambda } }}} + \gamma T$ | (6) |
式(6)用来对结构树q的质量进行评分. 该分数类似于评估决策树的杂质系数, 不同之处在于它是针对更广泛的目标函数而得出的. XGBoost本身的核心是基于梯度提升树实现的集成算法, 整体来说可以有3个核心部分: 集成算法本身, 用于集成的弱评估器, 以及应用中的其他过程.
梯度提升算法是XGBoost算法的基础, 它是实现模型预测的有力技术之一, 在Boosting算法中处于重要位置. 集成算法主要通过在数据集中生成弱评估器(n_estimators), 并将弱评估器集合起来, 效果优于单一的模型. n_estimators过小容易造成数据的欠拟合, 过多容易造成数据的过拟合问题. 所以如何选择合适的n_estimators是一个重点.
1.2 改进的网格搜索法网格搜索法(grid search)[16]是指将指定参数进行枚举, 通过将评估函数中的参数进行交叉验证得到最优参数的算法. 即把指定优化的参数在一定范围内依次排序, 并将这些数据排列成组合形成网格, 依次将数据放入分类器中进行训练, 并采用交叉验证方法对参数的表现进行评估, 在分类器遍历了所有的参数组合后, 返回一个最优的分类器, 同时获得最优的参数组合.
本文中对网格搜索法的实际应用是让eta与n_estimators在一定的范围内划分网格并遍历网格内所有点进行取值(数据为本文借贷数据), 其中eta的范围为[0.05, 1],步长为0.01, n_estimators的范围为[1, 300], 步长为3. 在此范围内得到eta与n_estimators下训练集分类准确率, 通过比较准确率来确定最优的参数组合. 参数的寻优如图1所示.

|
图 1 网格搜索法 |
从图1中能够知道, 参数eta和n_estimators在一定的区间范围内能够取得比较高的准确率, 但在其他的多数范围内的准确率并不高, 使得在进行参数寻优的过程中消耗大量的时间.
针对上述问题提出改进方法. 首先, 在参数区间上选择大步长进行参数寻优, 得到准确率高的最优局部参数. 再次, 在局部最优参数范围内采用小步长在该范围内进行二次寻优, 寻找最优参数. 改进的方法减少了不必要的计算, 节省了大量的时间.
2 改进的GS-XGBoost的个人信用评估模型改进的个人信用评估模型分为2部分, 第1部分为数据预处理过程, 首先将数据集进行极差标准化处理后进行特征选择, 筛选出重要性高的特征属性. 第2部分为模型的优化过程, 将筛选出的特征数据集进行改进的网格搜索法处理, 寻找最优参数n_estimators和learning rate. 随后将模型进行评估, 采用5折交叉验证法并取均值进行对比.
2.1 算法流程改进的GS-XGBoost的个人信用评估模型的流程图如图2所示.
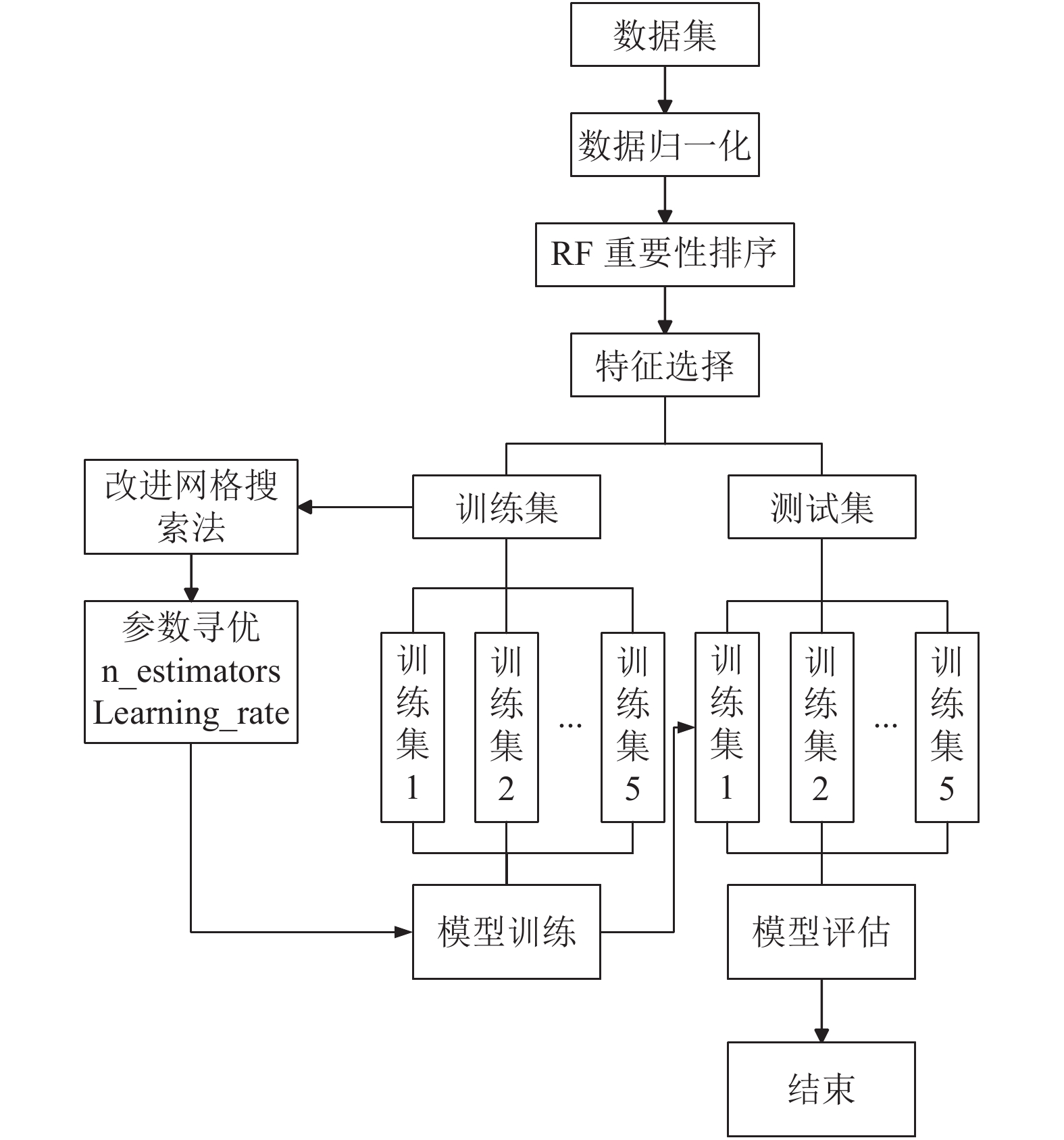
|
图 2 算法流程图 |
具体步骤如下:
步骤1. 数据预处理. 对数据进行建模分析之前, 需要对数据中的缺失值进行填补或删除. 之后, 对处理后的数据进行极差标准化处理, 公式如下:
| ${x^*} = \dfrac{{{x_{ij}} - \min ({x_j})}}{{\max ({x_j}) - \min ({x_j})}}$ | (7) |
其中,
步骤2. 特征选择. 数据集中的维数过高时, 不相关的属性特征对个人信用的评估之间并没有相互关联性, 影响个人评估的准确率. 通过特征选择可以提高模型的精确度, 预防过拟合. 本文采用随机森林算法(RF)对数据集进行训练, 取得每个特征的重要性排名并移除重要度低的特征属性.
步骤3. 参数寻优. 使用改进的网格搜索法对分类器的参数进行寻优.
1)将数据集D分为训练集
2)将产生的5组数据对分类器中的弱评估器(n_estimators)以及学习速率(learning_rate)进行训练, 使用改进的网格搜索法对XGBoost模型进行寻优, 得到最优参数.
步骤4. 模型评估. 将最优参数与特征子集代入模型中进行评估, 并与其它分类器进行比较.
2.2 评价指标本文选择
| 表 1 混淆矩阵 |
| $\left\{\begin{split} & \mathop R\nolimits_{{\rm{call}}} = \dfrac{{{T_p}}}{{{T_p} + {F_n}}} \\ & {{{P}}_{{\rm{recision}}}} = \dfrac{{{T_p}}}{{{T_p} + {F_n}}} \\ & F - value = \dfrac{{(1 + {\beta ^2}) \times {R_{{\rm{call}}}} \times {P_{{\rm{recision}}}}}}{{{\beta ^2} \times {R_{{\rm{call}}}} + {P_{{\rm{recision}}}}}} \\ \end{split} \right.$ | (8) |
| $\left\{\begin{split} & {N_{{\rm{accrance}}}} = \frac{{{T_n}}}{{{T_n} + {F_p}}} \\ & G - mean = \sqrt {{R_{{\rm{call}}}} \times {N_{{\rm{accrance}}}}} \\ \end{split} \right.$ | (9) |
为了检验本文改进算法的有效性, 对本文算法进行实证分析, 从UCI国际机器学习库中挑选出信用卡借贷数据. 数据的相关信息如表2所示. 属性相关信息如表3所示.
| 表 2 样本信息 |
| 表 3 特征属性 |
对数据集进行特征选择, 利用随机森林对数据集进行特征重要性排名, 结果如图3所示. 选取排名前12的特征属性数据集.

|
图 3 特征重要性排名 |
3.2 改进网格搜索法
为了比较改进算法的优越性, 将特征选择后的数据集进行参数寻优. 网格搜索法的变量为n_estimators和learning rate, 设定不同的步长范围, 分为4组数据进行比较. 第1组数据n_estimators的范围为(1, 300), 步长为5, learning rate的范围为(0.05, 1), 步长为0.05. 第2组数据n_estimators的范围为(1, 300), 步长为10, learning rate的范围为(0.1, 1), 步长为0.1. 第3组数据n_estimators的范围为(1, 300), 步长为20, learning rate的范围为(0.1, 1), 步长为0.1. 第4组数据n_estimators的范围为(1, 300), 步长为50, learning rate的范围为(0.1, 1), 步长为0.1, 结果如表4所示. 选择最优参数n_estimators为16, learning rate为0.44.
3.3 模型评估本文将改进后的模型进行评估. 经过特征选择后的数据集从20维下降为12维, 将特征选择后筛选的数据集作为分类器XGBoost的训练集进行训练, 使用改进的网格搜索法寻找XGBoost的最优参数n_estimators和learning rate. 本文使用软件为Python3.7, 使用5折交叉验证法对数据集进行训练来减少随机性对分类结果的影响. 本文算法模型(GS-XGB)与支持向量机(SVM)、随机森林(RF)、逻辑回归(LOG)、神经网络(BP)以及未改进的XGBoost (XGB)进行比较, 实验结果如表5和表6所示, F和G分别为
| 表 4 参数寻优结果比较 |
| 表 5 少数类准确率 |
| 表 6 模型实验结果对比 |
表5为各模型下少数类的准确率, 少数类为信用较差的用户. 从表中可以得到如下结论: 1)总体上每个模型下的少数类准确率都比较高, 差异较小, 但与其他模型相比, 该方法对信用评估的分类效果优于其他算法, 能够有较大的准确率识别信用不良人员. 2)与随机森林模型(RF)相比, 少数类分类的平均准确率提高了6.8%, 与未经过改进的XGBoost相比, 平均准确率提高了2.7%.
表6为各个评估模型在信贷数据集上的
随着个人信用贷款消费愈来愈普及, 个人信用良好与否直接导致信贷金融机构的损失, 因此对个人信用评估的研究非常重要. 本文提出了基于改进的GS-XGBoost的个人信用评估研究, 该方法将改进的网格搜索法应用于XGBoost模型, 筛选出最优参数n_estimators和learning rate. 选用UCI公开数据集进行评估, 使用
未来需要解决的问题有: 1)本文属于二分类问题, 对于多分类还需要进一步的研究. 2)该算法对本文数据集的有效性是否对其他数据也有效. 3)在特征选择上, 如何将该算法与其他方法相结合(如神经网络, 支持向量机等)进一步提高算法精确度.
| [1] |
Kozeny V. Genetic algorithms for credit scoring: Alternative fitness function performance comparison. Expert Systems with Applications, 2015, 42(6): 2998-3004. DOI:10.1016/j.eswa.2014.11.028 |
| [2] |
Ala'Raj M, Abbod M. Classifiers consensus system approach for credit scoring. Knowledge-Based Systems, 2016, 104: 89-105. DOI:10.1016/j.knosys.2016.04.013 |
| [3] |
Feng JZ, Wang Y, Peng J, et al. Comparison between logistic regression and machine learning algorithms on survival prediction of traumatic brain injuries. Journal of critical care, 2019, 54: 110-116. DOI:10.1016/j.jcrc.2019.08.010 |
| [4] |
谢娟英, 谢维信. 基于特征子集区分度与支持向量机的特征选择算法. 计算机学报, 2014, 37(08): 1704-1718. |
| [5] |
黄卿, 谢合亮. 机器学习方法在股指期货预测中的应用研究——基于BP神经网络、SVM和XGBoost的比较分析. 数学的实践与认识, 2018, 48(08): 297-307. |
| [6] |
唐耀先, 余青松. 消除属性间依赖的C4.5决策树改进算法. 计算机应用与软件, 2018, 35(03): 262-265, 315. DOI:10.3969/j.issn.1000-386x.2018.03.050 |
| [7] |
王黎, 廖闻剑. 基于GBDT的个人信用评估方法. 电子设计工程, 2017, 25(15): 68-72. DOI:10.3969/j.issn.1674-6236.2017.15.018 |
| [8] |
罗方科, 陈晓红. 基于Logistic回归模型的个人小额贷款信用风险评估及应用. 财经理论与践, 2017, 38(01): 30-35. |
| [9] |
Wang G, Hao J, Ma J, et al. A comparative assessment of ensemble learning for credit scoring. Expert Systems with Applications, 2011, 38(1): 223-230. DOI:10.1016/j.eswa.2010.06.048 |
| [10] |
Koutanaei FN, Sajedi H, Khanbabaei M. A hybrid data mining model of feature selection algorithms and ensemble learning classifiers for credit scoring. Journal of Retailing and Consumer Services, 2015, 27: 11-23. DOI:10.1016/j.jretconser.2015.07.003 |
| [11] |
He HL, Zhang W, Zhang S. A novel ensemble method for credit scoring: Adaption of different imbalance ratios. Expert Systems with Applications, 2018, 98: 105-117. DOI:10.1016/j.eswa.2018.01.012 |
| [12] |
刘潇雅, 王应明. 基于C4.5算法优化SVM的个人信用评估模型. 计算机系统应用, 2019, 28(7): 133-138. DOI:10.15888/j.cnki.csa.006958 |
| [13] |
王名豪, 梁雪春. 基于CPSO-XGboost的个人信用评估. 计算机工程与设计, 2019, 40(07): 1891-1895. |
| [14] |
Chen TQ, Guestrin C. XGBoost: a scalable tree boosting system. The 22nd ACM SIGKDD International Conference. San Francisco, CA, USA. 2016. 785–794.
|
| [15] |
Xia Y, Liu C, Li YY, et al. A boosted decision tree approach using Bayesian hyper-parameter optimization for credit scoring. Expert Systems with Applications, 2017, 78: 225-241. DOI:10.1016/j.eswa.2017.02.017 |
| [16] |
王健峰, 张磊, 陈国兴, 等. 基于改进的网格搜索法的SVM参数优化. 应用科技, 2012, 39(03): 28-31. |
 2020, Vol. 29
2020, Vol. 29



