2018年, 我国工业增加值在GDP中所占百分比为33.9%, 与1952年的17.6%相比, 在66年间增加了约两倍, 这说明我国工业的总体规模完成了从小变大的历史性突破. 就目前而言, 我国制造业在生产能力利用效率方面仍然处于比较低的水平. 这是因为传统制造业的生产调度模式已无法适应供应链体系的快速变化. 因此, 要对生产车间调度模式进行深入研究, 将传统的生产车间调度模式向智能化和高效化的方向发展.
智能和高效的生产调度模式不仅仅与机器和工件所处的状态有关, 还与在加工过程中所存在的多种客观因素有关. 我国正在大力支持对数字化车间的建设, 解决制造设备在制造能力方面的自治问题. 如今, 国内各生产加工企业以实现《智能制造2025》目标为契机, 大力推进生产调度智能化, 建立智能型工厂.
本文针对车间调度问题的特点对Q学习算法的主要要素进行重新设计, 使其与求解车间调度问题相适应, 并将设计好的算法对作业车间调度问题的标准化算例进行测试, 评估该方法的合理性.
1 国内外研究综述作业车间调度涉及时间和资源约束下的活动排序以满足给定的目标[1]. 由于目标冲突、资源有限以及难以准确建模模拟真实场景, 因此是一个复杂的决策活动. 在制造环境中, 调度活动映射到操作和资源到机器. 调度器的目的是确定每个操作的开始时间, 以便在满足容量和技术约束的同时实现期望的性能度量. 在当今高度竞争的制造环境中, 明确需要能够在可接受的时间范围内产生良好解决方案的健壮和灵活的方法. 对解空间的搜索过程以识别最优调度的算法的计算时间随着问题大小呈指数增加.
近五年来, 国内外针对作业车间调度问题的研究主要聚焦在两个方向, 一是通过自适应搜索的方法对该问题进行求解. 二是使用机器学习工具来研究调度过程, 以获得任何新问题的调度.
1.1 自适应搜索方法国外肯定了运用智能算法对求解作业车间生产调度(Job-shop Scheduling Problem, JSP)问题具有十分重要的作用. 其中, Kurdi等[2]在遗传算法中加入了新岛模型, 解决了目标为最大完工时间的作业车间调度问题, 但在其他优化问题中尚未验证其有效性; Asadzadeh等[3]用并行人工蜂群算法(PABC)求解作业车间生产调度问题, 该算法收敛速度非常快, 且求解质量高; Silva等[4]用转移瓶颈程序来解决车间作业调度问题, 尽管最小化了生产时间, 但是难以在寻求全局解决办法方面实现多样化; Mudjihartono等[5]提出了将粒子群算法加入到遗传算法中, 设计出能够实现并行编程的新算法, 该算法求解效果较好, 但在非并行算法中, 由于问题大小的增加使得整个算法的求解速度大大减慢.
国内关于求解JSP调度问题的主要方法同样是利用群智能优化算法. 其中, Shen等[6]将处理调度问题的处理时间不确定性考虑在内, 建立了不确定机会约束模型. 结果表明, 对于不确定性作业车间调度问题, 萤火虫优化算法可以得到比粒子群优化算法更好的结果; 沈桂芳等[7]将随机均匀设计法(RUDHS)与协调搜索优化算法相结合, 对JSP典型测试用例进行了仿真, 其结果表明, RUDHS算法具有更高的效率; 杨小东等[8]对作业车间调度问题, 提出了分布式算法(TSEDA), 为了保证解决方案的可行性, 采用了编码和解码的机制; 顾文斌等[9]用生物启发的方法对粒子群优化算法进行改进, 使作业车间调度的最大总处理时间最小; 施文章等[10]将模拟退火方法引入到布谷鸟搜索算法中, 并在标准车间调度问题中使用改进的作业车间调度问题; Li等[11]对传统的TLBO进行了改进, 以提高对JSP的解决方案的多样化和集约化, 计算时间有待提升; 陈宇轩[12]通过区间数对不确定过程的加工时间进行表征, 研究了具有不确定加工时间特征的柔性作业车间调度问题; Zeng等[13]将区间数理论引入遗传算法的变异过程中, 用改善后的遗传算法求解柔性作业车间调度问题; 钱晓雯[14]提出一种基于可变邻域搜索的动态焰火算法, 用于求解具有最小化最大完工时间为特征的作业车间调度问题(JSP). 在标准算例集中, 该算法具有一定的鲁棒性, 提高了优化精度和收敛性; Zhang等[15]研究了在具有动态性的制造环境中的柔性装配作业车间调度问题, 发现约束规划是解决此问题的有效方法, 其解的适应性优于混合整数线性规划以及静态和动态情况下的所有调度规则.
1.2 主动调度算法与机器学习工具相结合的方法相对于作业序列优化, 近年来关于主动调度算法与机器学习工具相结合的国内外相关文献较少. 曹琛祺等[16]通过对调度队列进行变换, 将原来排序的调度问题转化为了可分类的调度问题, 构造出基于人工神经网络的分类器. 对于新的调度实例, 使用训练好的分类器来导出优先级, 然后使用优先级来获得调度序列; Tselios等[17]提出一个混合方法来处理作业车间调度问题. 该方法包括3个阶段: 第一阶段利用遗传算法产生一组初始解, 在第二阶段作为递归神经网络的输入. 在第三阶段, 使用自适应学习速率和类似禁忌搜索的算法, 以改进递归神经网络返回的解; Shahrabi等[18]提出了一种基于可变邻域搜索(VNS)的调度方法. 考虑到事件驱动策略, 为了在任何重新调度点获得VNS的适当参数, 使用Q学习算法进行强化学习; Waschneck等[19]将谷歌的深度强化学习网络应用于作业车间生产调度, 实现了工业4.0的生产控制; Kuhnle等[20]设计了一种用于自适应订单调度的强化学习算法, 提出了强化学习算法在车间生产系统中的评价方法和准则.
2 作业车间调度问题描述与定义JSP问题可描述为: n个工件在指定的m台机器上进行加工, 工件可用一个集合workpiece (WP)表示, 机器可用一个集合machine (MC)表示. 各工件在各机器上的工序事先给定, 目标是使得某些加工性能指标达到最优. 本论文用于衡量加工性能的指标是使最大完工时间最小化.
为了确保作业车间能够正常运行, 设定的约束条件有: 各工件经过其准备时间后即可开始加工; 在每个加工阶段, 有且仅有一台机器对同一个工件进行加工, 每个工件也只能是由一台机器对其进行加工; 一个操作一旦开始就不允许中途间断, 整个加工过程中机器均有效; 各工件必须按事先规定的工艺路线对其进行加工; 不考虑工件的优先权; 各工件的操作需等待.
| ${{Z = }}\min \left( {{{{C}}_{\max }}} \right)$ | (1) |
| ${{{C}}_{ik}} - {T_{ik}} + M(1 - {S_{ihk}}) \ge {C_{ih}}$ | (2) |
| ${{{C}}_{jk}} - {C_{ik}} + M\left( {1 - {{{X}}_{ijk}}} \right) \ge {T_{jk}}$ | (3) |
| ${C_{jk}} \ge 0$ | (4) |
| ${S_{ihk}},{X_{ijk}} \in \left\{ {0,1} \right\}$ | (5) |
| $i,j \in \left\{ {1,2,\cdots,n} \right\}$ | (6) |
| $h,k \in \left\{ {1,2,\cdots,m} \right\}$ | (7) |
其中, 式(1)为目标函数Z, Cmax用来表示最大完工时间makespan; 第一个约束条件为式(2), 用来表示工序之间的先后约束关系, Cik表示第i个工件在第k台机器上的完工时间, Tik表示第i个工件在第k台机器上的加工时间, M为一个无穷大数, Sihk表示工件i在机器h和机器k上加工的先后顺序, 若机器h先于机器k加工工件i, Sihk取值为1, 否则为0, Cih表示第i个工件在第h台机器上的完工时间; 第二个约束条件式(3)表示工序无抢占行为, Cjk表示第j个工件在第k台机器上的完工时间, Xijk表示工件i和工件j在同一台机器K上进行加工的先后顺序, 若工件i先于工件j在机器k上进行加工, 则Xijk取值为1, 否则为0, Tjk表示第j个工件在第k台机器上的加工时间, 第三个约束条件式(4)表示总的完工时间为非零值. 第4~6个约束条件即式(5)~式(7)是具体的取值范围.
3 强化学习与Q学习算法概述 3.1 强化学习定义首先, 可将机器学习领域按学习模式划分为监督学习、无监督学习以及强化学习[19]. 强化学习(Reinforcement Learning, RL)是机器学习的一个分支. 其次, RL是一种以目标为导向的学习, 智能体以“试错”的方式来进行学习, 通过与环境进行交互获得奖励指导行为[20]. 其目标是使智能体所获得的奖励最大化.
具体而言, RL解决的问题是, 针对一个具体问题得到一个最优的策略, 既在当前状态下采取的最佳行为, 使得在该策略下获得的长期回报能够达到最大.
在RL中, 算法将外界环境以奖励量最大化的方式展现, 该算法没有直接对智能体所应该采取的动作或行为进行指导, 而是智能体通过动作所对应的奖励值的多少来采取行动.
对于智能体所选择的行为, 其不只是影响到了瞬时所获得的奖励, 而且还对接下来的行为和最终获得的奖励和产生影响.
3.2 强化学习模型在当前状态下, 智能体执行了一个动作, 并与环境进行交互, 然后得到下一个轮次的奖励, 以及进入到下一个轮次的状态中去, 依此循环往复.
奖励: 通常记作Rt, 表示第t个时间段的返回奖励值, 是一个标量, 回报是所有即时奖励的累积和.
行为: 通常记作Action, 是来自于动作空间, 可以是连续的动作, 也可以是离散动作.
状态: 是指当前智能体所处的状态.
策略: 是指智能体在特定状态下的行为依据, 是从状态到动作的映射, 规定了智能体应该采取的动作的概率分布. 函数定义为a=π(s), 即输入为状态s, 输出为行为a. 作为RL中最为重要的内容, 策略设计的质量与智能体所采取的行动以及算法的整体性能息息相关.
策略可分为确定策略和随机策略. 确定策略就是某一状态下的确定动作, 而随机策略是以概率来描述, 即某一状态下执行这一动作的概率, 如式(8)所示.
| $\pi \left( {a|s} \right) = P\left[ {{A_t} = a|{S_t} = s} \right]$ | (8) |
如果对状态转移矩阵不加以考虑, 智能体与环境的互动接口应包括行动、即时奖励和所属的状态.
如图1所示, 智能体与环境的一个交互过程可准确的表述为: 在St状态下执行At这一动作, 然后在t+1时间先得到即时奖励Rt+1. 每一步, 智能体工具策略选择一个行动执行, 然后感知下一个状态和即时回报, 通过经验再修改自己的策略.
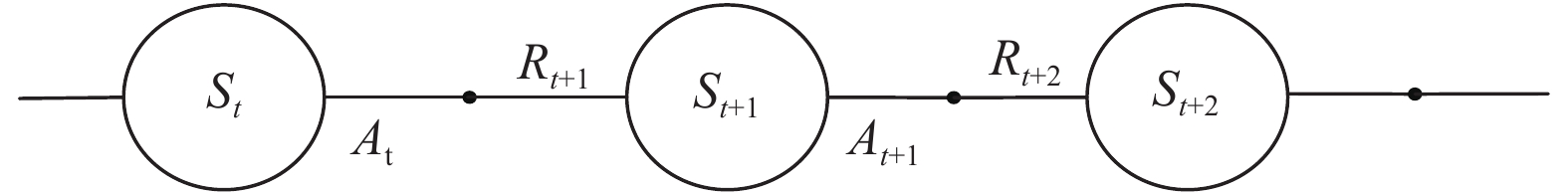
|
图 1 能体与环境的交互过程 |
3.3 Q学习算法概述
Q学习算法(Q Learning, QL)的伪代码如下:
Initialize
Repeat(for each episode):
Initialize S
Repeat(for each step of episode):
Choose A from S using policy derived from Q
Take action A, observe R, S'
| ${{Q}}\left( {s,a} \right) \leftarrow {{Q}}\left( {s,a} \right) + \alpha \left[ {{{R + }}\gamma {{\max }_a}Q\left( {s',a} \right) - Q(s,a)} \right]$ |
| ${{s}} \leftarrow s'$ |
Until s is terminal
该算法中, 采样数据阶段, 为了保证一定的探索性, 采用 策略. 在更新Q值时, 采用完全贪婪策略, 即直接选Q值最大的动作, 与当前的行动策略无关[21].
由于Q学习算法并不关注智能体行动时所遵循的策略, 而仅仅是采取最好的Q值, 其学习的规则与实行的规则不用, 因此, 这是一种异策略的学习算法. 学习流程如图2所示.

|
图 2 QL算法流程 |
具体步骤如下:
1)初始化Q函数为某一任意值.
2)根据ε贪婪策略, 在状态下执行某一行为, 并转移到新状态.
3)根据式(9)更新规则更新上一状态的Q值.
| ${{Q}}\left( {s,a} \right) = {{Q}}\left( {s,a} \right) + \alpha \left( {r + \gamma \max Q\left( {s',a'} \right) - Q\left( {s,a} \right)} \right)$ | (9) |
4)重复步骤2)和3), 直到达到最终状态.
4 适用于作业车间调度问题的Q学习算法 4.1 策略的设定一般用于求解JSP问题的Q学习算法是将行为和需要加工的工件一一对应, 作为该算法的可选策略[22], 以标准算例ft06为例, 如表1所示. 此外, 每个工件所对应的状态有两个, 即在加工状态和待加工状态, 因此, 状态数为工件的2n. 这样设置的原因是一般用于求解JSP问题的Q学习算法所学习的对象是各个工件加工的顺序. 由于这与JSP问题中工件实际所处的状态存在一定的偏差, 因而影响了调度性能.
| 表 1 一般Q学习算法的策略设定 |
本文提出的改进的Q 学习算法(Improved Q-Learning algorithm, IQL)所学习的对象不是各个工件加工的优先级, 而是策略选择的优先级, 通过不断试错, 直接按不同策略所反馈的奖励值大小来选择策略, 从而间接地决定工件的加工顺序. 具体如表2所示, 设定5个基本动作分别对应5种不同的状态, 动作和所对应的状态共同构成了策略. 其中, Action1偏向于加工当前阶段落后的工作; Action2偏向于加工下一阶段耗时最短的工作; Action3偏向于加工当前阶段领先的工作; Action4偏向于加工下一阶段耗时最长的工作; Action5该机器闲置.
| 表 2 改进的Q学习算法的策略设定 |
4.2 智能体介入调度的选择
分别对以下两种情况进行选择:
第1种情况: 当前无可选进程.
既没有空闲的机器, 或者没有处于闲置态的作业. 此时不需要智能体介入调度, 各台机器只需要继续对当前工件进行当前工序的加工即可.
第2种情况: 存在可选进程.
既机器完成了某个工件的某道工序作业, 呈空闲状态, 且还有某些工件存在某些工序需要加工. 此时, 需要智能体介入调度.
4.3 智能体介入调度的选择根据作业车间调度的特点, 综合考虑了两种实际情况来对奖励制度进行设置:
1)平均总的机器加工效率与奖励成正比
| ${{PET}} = \frac{{TC}}{{TS}}$ | (10) |
如式(10)所示, 加工效率PET就是总的任务完成的时间TC与耗费时间TS的比值. 可以看出, 总的任务完成时间不变的情况下, 耗费时间越短, 加工效率越高. 由于在作业车间调度问题中, 每个工件加工有给出固定的加工阶段, 即每个工件所对应的加工次序存在先后顺序, 每道工序有其固定的加工时间. 所以, 最后完成加工工作所耗费的时间肯定是大于等于固定需要的时间. 耗费时间越接近固定需要的时间, 说明浪费的时间少, 加工效率高, 得到的奖励也就越多.
2)加工消耗时间与惩罚成正比
这里设置了一个与加工时间成平方关系的惩罚. 这是本文的关键点也是创新所在, 因为在刚开始加工时候, 需要加工的任务多, 选择多, 可以很容易把机器安排得非常紧凑, 决策显得作用并不是特别大. 但是随着加工进度推进后, 决策的难度越高, 很容易出现前面阶段调度得很好, 但是后面阶段就差了. 这里设置平方关系后, 到后面每耗费多一个时间, 扣罚是快速增长的. 从而迫使智能体在加工后期也非常谨慎调度.
根据奖惩制度设置的瞬间奖励更新函数如式(11)所示, 其中,JRT为剩余加工时间, 总的任务完成时间TC与剩余加工时间JRT的差值表示当前完工时间, 表示加工阶段, 当前完工时间与加工阶段的比值表示平均各阶段的完工时间, 是一个惩罚函数, 表示越是临近完工, 相应的惩罚也就越大, 调度也会变得越加谨慎.
| ${{reward}} = reward + \frac{{TC - JRT}}{{tick}} - 0.000\;01\times tic{k^2}$ | (11) |
该奖惩制度的设置, 与一般用于求解JSP问题的Q学习算法中的奖励设置有明显的不同[23]. 通常, 在用Q学习算法求解此类问题中, 选择两种特征参数, 比如作业平均松弛时间和剩余作业的平均执行时间, 其比值的大小反映了当前的调度效率, 通过比值, 人为地将整个调度状态空间划分为一维的m个状态, 然后针对每一种状态, 指定一个具体的数值来表示奖惩. 其缺点在于忽视了车间调度规则的复杂性, 仅凭两个特征参数的比值无法对当前调度的好坏做充分的评价.
JSP问题的Q学习的更新过程如式(12)所示.
| $\begin{split} {{{Q}}_{\rm new}} =& Q + \alpha \times \left[ {reward + \frac{{TC - JRT}}{{tick}} - 0.000\;01\times tic{k^2} } \right.\\ &+\left. {discoun{t_{\rm factor}}*{Q_{\rm Ma{x_{ next}}}} - Q} \right] \end{split}\!\!\!\!\!\!\!\!\!\!\!\!$ | (12) |
IQL算法会创建一个Q表用来保存每个状态所对应的Q值, 由式(12)可知, 与状态
假设下一个状态
| $\begin{split} {{{Q}}_{\rm new}} =& \left( {1 - \alpha } \right)Q + \alpha \times \left[ {reward + \frac{{TC - JRT}}{{tick}} } \right.\\ &\left. - {0.000\;01\times tic{k^2} + discoun{t_{\rm factor}}*{Q_{\rm Ma{x_{next}}}}} \right] \end{split}$ | (13) |
对式(13)进行第一次迭代, 如式(14)所示, 迭代n次后, 如式(15)所示, 收敛证明过程如式(14)~式(17)所示.
| $\begin{split} {Q_{\rm new}} =& {\left( {1 - \alpha } \right)^2}Q + \left( {1 - \alpha } \right)\alpha \times \left[ {reward + \frac{{TC - JRT}}{{tick}} } \right.\\ &\left. -{0.000\;01\!\times\! tic{k^2} \!+\! discoun{t_{\rm factor}}\!\times\!{Q_{\rm Ma{x_{next}}}}} \right] \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!$ | (14) |
| $\because {{n}} \to \infty ,\left( {1{\rm{ - }}\alpha } \right) \subset \left( {0,1} \right)$ | (15) |
| $\therefore {\lim\nolimits _{n \to \infty }}{\left( {1{\rm{ - }}\alpha } \right)^{{n}}} \to 0$ | (16) |
| $\begin{split} {{{Q}}_{\rm new}} =& reward + \frac{{TC - JRT}}{{tick}} - 0.000\;01\times tic{k^2} \\ &+ discoun{t_{\rm factor}}\times{Q_{\rm Ma{x_{next}}}}\\ =& reward + \frac{{TC - JRT}}{{tick}} - 0.000\;01\times tic{k^2}\\ &+ discoun{t_{\rm factor}}\times{Q_{{\rm{next}}}} \end{split}$ | (17) |
此时,
选择标准算例库中的abz5、abz7、abz9、ft06、ft10、ft20、la01、la02、la03、la04、la06、la11、la16、la21、la26、la31、swv06、swv16、yn1、yn2和yn3共21个不同规模大小的算例, 对用于求解JSP问题的IQL算法进行验证, 将该算法中的参数: 学习率、折扣因子和贪婪因子, 分别设置为0.1、0.97和0.8.
算法的运算环境为Windows 10专业版64位操作系统, Intel(R)Core(TM)i5-4300U CPU @2.50GHz处理器, 8 GB RAM. 算法的编程实现软件为Python 3.6版本, 用于测试和比较的算法均重复独立运行20次, 求得最小值和均值.
为了能更好的与文献中提到的混合灰狼优化算法(Hybrid Gray Wolf Optimization, HGWO)[24]、离散布谷鸟算法(Discrete Cuckoo Search, DCS)[25]和量子鲸鱼群优化算法(Quantum Whale Swarm Optimization, QWSO)[26]进行比较, 各算法的参数设置与文献保持一致, 具体设置如下:
1) HGWO: 种群规模设为30, 最大迭代次数为500, 独立运行次数为30.
2) DCS: 鸟窝的个数为30, 宿主发现外来鸟蛋的概率为0.25.
3) QWSO: 所有鲸鱼个体先进行基本位置更新操作, 然后进行量子旋转操作, 迭代开始为其启动时机, 启动概率为1.
此外, 为了便于比较, 选择最小值误差率和平均值误差率这两个指标来衡量不同算法的求解性能. 最小值误差率为该算法所求的最小值与已知最优解的差与已知最优解之比, 用来衡量算法所能求得的最优解与已知最优解的接近程度, 该值越小, 说明算法求解的寻优质量越优. 平均值误差率为该算法所求的平均值与已知最优解的差与已知最优解之比, 用来衡量各个算法在独立运行20次后的平均值与已知最优解的接近程度, 该值越小, 表明算法求解的总体质量越优.
5.1 回报函数曲线变化分析以算例ft06、ft10和ft20为例, 回报函数曲线变化如图3~图5所示, 在迭代近6000次后, 回报函数均趋于稳定状态, 且在训练过程中曲线无明显波动, 说明学习过程比较平稳, 并与数据规模无关.
5.2 寻优收敛曲线分析与文献[19]进行对比, 以ft06、ft10、ft20算例为例, 如图6~图8所示, 可以看出IQL算法在收敛速度上有显著提高.
与3种群智能算法进行对比, 以ft10算例为例, 寻优曲线变化如图9所示, IQL算法的收敛速度远低于群智能算法, 这说明还有进一步提高的可能性.

|
图 3 算例ft06的回报函数曲线变化 |

|
图 4 算例ft10的回报函数曲线变化 |

|
图 5 算例ft20的回报函数曲线变化 |
IQL算法的收敛速度明显慢于群智能算法, 是因为此算法的求解过程是一个对策略的选择不断进行探索, 不断试错的过程, 学习的目标是使奖励值最大所对应的策略, 是间接寻优的过程. 而群智能算法则是以寻找最优解为其目标, 通过对数据进行编码, 以一定规则进行寻优后解码, 是直接寻优的过程.

|
图 6 算例ft06的Q学习算法收敛对比 |
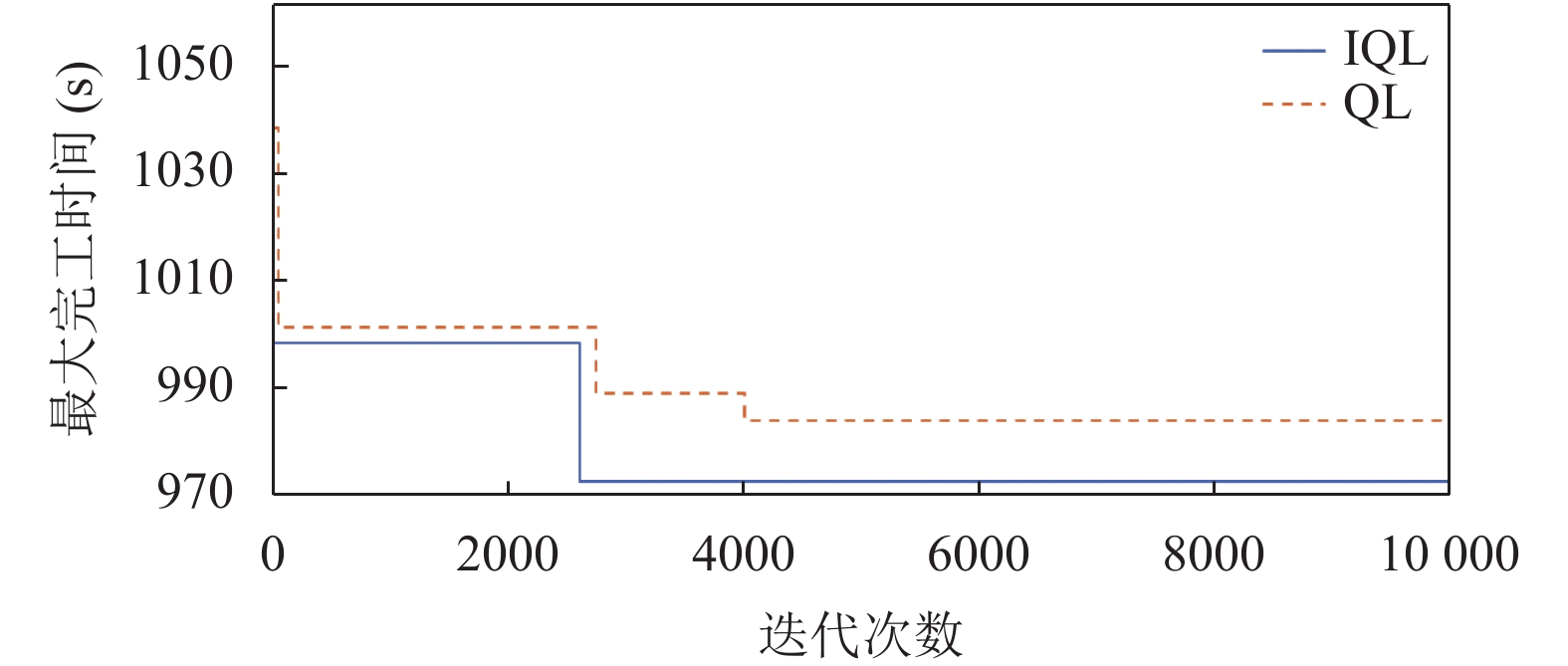
|
图 7 算例ft10的Q学习算法收敛对比 |
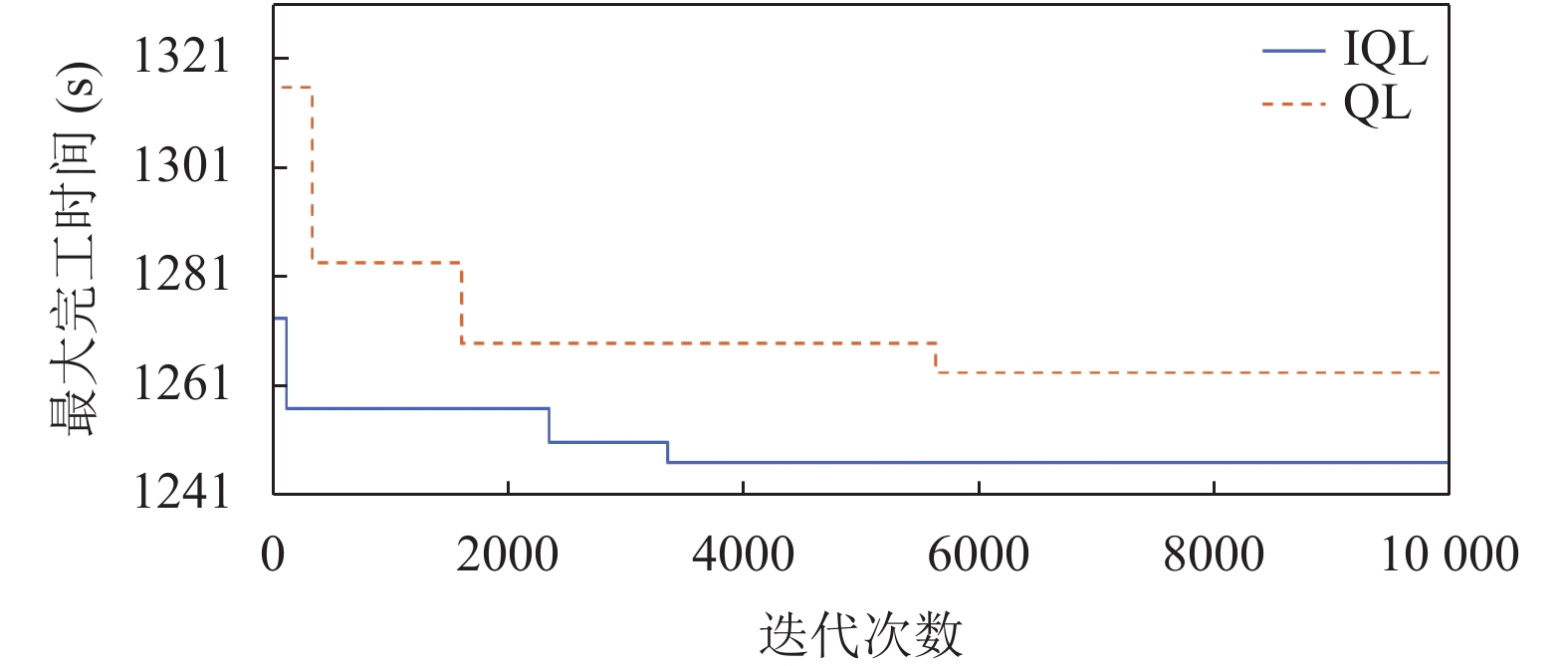
|
图 8 算例ft20的Q学习算法收敛对比 |

|
图 9 算例ft10的3种群智能算法的寻优曲线变化 |
5.3 求解结果对比分析 5.3.1 IQL算法与已知最优解的对比分析
从表3中可以看出, IQL算法的最小值误差率(IQLmin error rate)为0的有4个算例, 在3%以内的算例有7个, 在5%以内的算例有11个, 在10%以内的算例有16个, 约占所有算例的76%. 图12为算例ft10的调度结果.
5.3.2 IQL算法与QL算法的对比分析表4为这两种算法的最小值误差率(min error rate)、平均值误差率(avg error rate), 分别对这两种指标进行方差分析.
首先, 对最小值误差率和平均值误差率进行配对样本T检验, 结果如表5所示, 以小值误差率的检验结果为例, 均值X约为–0.130, 标准差SD为0.142, 成对差分均值的标准误SE为0.031, 置信区间CI为[–0.195, –0.065], α值小于0.05说明IQL算法与QL算法在求解质量上具有显著差异, 配对T检验的t值为负数(–4.183), 说明IQL算法在寻优质量上显著优于QL算法. 具体而言, 如表5所示, 求解质量提升率超过5%的有12个算例, 超过10%的有7个算例, 超过20%的有6个算例.
| 表 3 IQL算法与已知最优解的对比 |
| 表 4 IQL算法与QL算法在误差率上的方差分析结果 |
同理, 从平均值误差率的配对样本T检验结果可以看出, IQL算法在总体性能上显著优于QL算法.
5.3.3 IQL算法与HGWO算法、DCS算法和QWSO算法的对比分析HGWO算法、DCS算法和QWSO算法的最小值误差率和平均值误差率以文献[24–26]中的数据为准, 与IQL算法的结果进行配对样本T检验, 结果如表6所示, 以最小值误差率的检验结果为例, 在与HGWO算法的比较中, α大于0.05, t值为1.093, 说明IQL算法与HGWO算法在求解结果上无显著差异; 与DCS算法和QWSO算法的比较中, α值均小于0.05, 说明求解结果存在着显著差异, t值均为负数, 说明IQL算法在求解质量上显著优于DCS算法和QWSO算法. 具体而言, 如表6所示, 求解质量优于HGWO算法的有9个算例, 约占所有算例的42.86%; 求解质量优于DCS算法的有15个算例, 约占所有算例的71.43%; 求解质量优于QWSO算法的有17个算例, 约占所有算例的80.95%.
| 表 5 IQL算法与QL算法的求解结果 |
| 表 6 IQL算法与QL算法的求解结果 |
同理, 在平均值误差率的配对样本T检验结果中可以发现, 改近的Q学习算法在总体性能上显著优于其它3种算法.
6 总结与展望 6.1 总结从经典的作业车间调度问题模型出发, 对一般用于求解该问题的Q学习算法进行改进, 设计出与该问题更为匹配的改进的Q学习算法, 通过用21个标准算例对其进行测试, 选择最小值误差率和平均值误差率作为评估算法的求解质量和总体性能指标, 与改进前的Q学习算法和3种群智能算法进行对比, 得出以下3种结论:
1)在收敛速度方面, 改进的Q学习算法快于改进前的Q学习算法, 慢于改进的灰狼优化算法、离散布谷鸟算法和量子鲸鱼群优化算法, 这与强化学习不断“试错”的寻优特点有关.
2)在求解质量方面, 改进的Q学习算法显著优于改进前的Q学习算法, 离散布谷鸟算法和量子鲸鱼群优化算法, 与改进的灰狼优化算法无显著差异.
3)在总体性能方面, 改进的Q学习算法显著优于改进前的Q学习算法、改进的灰狼优化算法、离散布谷鸟算法和量子鲸鱼群优化算法.
6.2 展望改进的Q学习算法在求解作业车间调度问题中, 具有良好的理论价值和实际应用意义, 丰富了强化学习的研究内容, 拓展了Q学习算法的应用范围, 为相关领域提供了有益的参考价值. 但是, 本文的研究仍然存在有待进一步改进的地方:
1)对调度问题的寻优速度有待提升. 本文算法对作业车间调度问题的求解效果和整体性能上优于同类Q学习算法和群智能算法, 但在寻优速度上, 显著慢于群智能算法. 说明该算法还有进一步改进的空间.
2)尝试更为丰富的调度问题. 本文算法所应用的调度场景为车间调度问题中的作业车间调度问题. 在后续工作中, 可以将算法引入到求解多目标的调度问题中, 扩大其应用场景.
| [1] |
Błażewicz J, Domschke W, Pesch E. The job shop scheduling problem: Conventional and new solution techniques. European Journal of Operational Research, 1996, 93(1): 1-33. DOI:10.1016/0377-2217(95)00362-2 |
| [2] |
Kurdi M. An effective new island model genetic algorithm for job shop scheduling problem. Computers & Operations Research, 2016, 67: 132-142. |
| [3] |
Asadzadeh L. A parallel artificial bee colony algorithm for the job shop scheduling problem with a dynamic migration strategy. Computers & Industrial Engineering, 2016, 102: 359-367. |
| [4] |
Silva MR, Cubillos C, Paniagua DC. A constructive heuristic for solving the Job-Shop Scheduling Problem. IEEE Latin America Transactions, 2016, 14(6): 2758-2763. DOI:10.1109/TLA.2016.7555250 |
| [5] |
Mudjihartono P, Jiamthapthaksin R, Tanprasert T. Parallelized GA-PSO algorithm for solving Job Shop scheduling problem. Proceedings of the 2016 2nd International Conference on Science in Information Technology. Balikpapan, Indonesia. 2016. 103–108.
|
| [6] |
Shen JY, Zhu YG. Chance-constrained model for uncertain job shop scheduling problem. Soft Computing, 2016, 20(6): 2383-2391. DOI:10.1007/s00500-015-1647-z |
| [7] |
沈桂芳, 李敬明, 陈平. 基于RUD的和声搜索算法求解作业车间调度问题. 江苏师范大学学报(自然科学版), 2017, 35(4): 58-61. |
| [8] |
杨小东, 康雁, 柳青, 等. 求解作业车间调度问题的禁忌分布估计算法. 计算机工程与应用, 2017, 53(7): 147-153. DOI:10.3778/j.issn.1002-8331.1510-0004 |
| [9] |
顾文斌, 张薇薇, 苑明海. 基于改进型粒子群的作业车间调度问题研究. 机械设计与制造工程, 2017, 46(1): 11-15. DOI:10.3969/j.issn.2095-509X.2017.01.002 |
| [10] |
施文章, 韩伟, 戴睿闻. 模拟退火下布谷鸟算法求解车间作业调度问题. 计算机工程与应用, 2017, 53(17): 249-253, 259. DOI:10.3778/j.issn.1002-8331.1612-0100 |
| [11] |
Li LN, Weng W, Fujimura S. An improved teaching-learning-based optimization algorithm to solve job shop scheduling problems. Proceedings of the 2017 IEEE/ACIS 16th International Conference on Computer and Information Science. Wuhan, China. 2017. 797–801.
|
| [12] |
陈宇轩. 工时不确定条件下基于改进遗传算法的柔性作业车间调度问题的区间数求解方法. 机械工程师, 2018(1): 74-76. DOI:10.3969/j.issn.1002-2333.2018.01.025 |
| [13] |
Zeng R, Wang YY. A chaotic simulated annealing and particle swarm improved artificial immune algorithm for flexible job shop scheduling problem. EURASIP Journal on Wireless Communications and Networking, 2018, 2018(1): 101. DOI:10.1186/s13638-018-1109-2 |
| [14] |
钱晓雯. 求解作业车间调度问题的变邻域动态烟花算法. 实验室研究与探索, 2018, 37(1): 19-21, 124. DOI:10.3969/j.issn.1006-7167.2018.01.006 |
| [15] |
Zhang SC, Wang SY. Flexible assembly job-shop scheduling with sequence-dependent setup times and part sharing in a dynamic environment: Constraint programming model, mixed-integer programming model, and dispatching rules. IEEE Transactions on Engineering Management, 2018, 65(3): 487-504. DOI:10.1109/TEM.2017.2785774 |
| [16] |
曹琛祺, 金伟祖. 基于人工神经网络的作业车间调度算法. 电脑知识与技术, 2016, 12(30): 204-207. |
| [17] |
Tselios DC, Savvas IK, Kechadi MT. Integrated intelligent method for solving multi-objective MPM job shop scheduling problem. Proceedings of the 2015 6th International Conference on Information, Intelligence, Systems and Applications. Corfu, Greece. 2015. 1–6.
|
| [18] |
Shahrabi J, Adibi MA, Mahootchi M. A reinforcement learning approach to parameter estimation in dynamic job shop scheduling. Computers & Industrial Engineering, 2017, 110: 75-82. |
| [19] |
Waschneck B, Reichstaller A, Belzner L, et al. Optimization of global production scheduling with deep reinforcement learning. Procedia CIRP, 2018, 72: 1264-1269. DOI:10.1016/j.procir.2018.03.212 |
| [20] |
Kuhnle A, Schäfer L, Stricker N, et al. Design, implementation and evaluation of reinforcement learning for an adaptive order dispatching in job shop manufacturing systems. Procedia CIRP, 2019, 81: 234-239. DOI:10.1016/j.procir.2019.03.041 |
| [21] |
Spanò S, Cardarilli GC, Di Nunzio L, et al. An efficient hardware implementation of reinforcement learning: The Q-learning algorithm. IEEE Access, 2019(7): 186340-186351. |
| [22] |
刘想德. 基于自适应规则的车间实时调度方法研究. 组合机床与自动化加工技术, 2014(2): 157-160. |
| [23] |
王超, 郭静, 包振强. 改进的Q学习算法在作业车间调度中的应用. 计算机应用, 2008, 28(12): 3268-3270. |
| [24] |
姚远远, 叶春明. 求解作业车间调度问题的改进混合灰狼优化算法. 计算机应用研究, 2018, 35(5): 1310-1314. DOI:10.3969/j.issn.1001-3695.2018.05.007 |
| [25] |
姚远远, 叶春明. 作业车间调度问题的布谷鸟搜索算法求解. 计算机工程与应用, 2015, 51(5): 255-260, 265. DOI:10.3778/j.issn.1002-8331.1304-0305 |
| [26] |
闫旭, 叶春明, 姚远远. 量子鲸鱼优化算法求解作业车间调度问题. 计算机应用研究, 2019, 36(4): 975-979. |
 2020, Vol. 29
2020, Vol. 29


