随着智能时代的到来, 生产数据价值的重要性越来越明显. 如何根据生产工艺, 通过数据采集、处理、聚类、存储、分析和可视化等技术手段发挥数据蕴含的价值信息, 成为了热门的研究课题. 而流程型制造车间的生产环境特殊, 加上传输网络、人为因素的影响, 导致采集到的生产数据不可避免的存在一定程度的异常情况, 如数据缺失、离群和异常波动等[1,2], 若不经过处理, 无法正常应用.数据处理就是为了清洗掉生产现场各种因素干扰造成的异常情况, 同时也为了面向生产管控需求进行特定的数据加工[3,4].
目前, 数据处理技术非常广泛[5,6], 如文献[7]针对复杂装备的监测数据在采集过程中出现时序混乱, 影响对设备状态的分析问题进行了建模研究, 根据不同实时任务对数据的时序容错性和实时性要求不同, 采用不同大小的缓冲窗口和处理策略, 并结合数据传输延时的概率密度, 分析计算模型的参数, 最后以仿真实验的方式验证了所提出模型的有效性; 文献[8]针对流程型制造业个性化的环境中生产工艺参数难以快速决策影响实时管控任务的问题, 通过结合实际生产工艺进行分析, 提出了基于数据驱动的生产工艺参数匹配方法, 建立了产品工艺相似度函数, 从大量生产数据中选取与实际生产任务有关的邻近数据, 通过对比历史数据与目标产品的生产要求实现了生产工艺参数的匹配; 文献[9]通过分析已有时间序列数据处理的研究, 进行了大量的实验研究, 结果表明, 在特殊情况下某些观点可能太乐观, 最后重新实现了一些时间序列表示形式和相似性度量; 文献[10]和文献[11]针对缺失数据的异常情况, 基于EM插补算法和高斯混合模型进行改进优化, 提出一种新的数据流缺失处理算法, 有效的解决了数据缺失异常, 最后通过实验验证, 相比于传统的EM插补算法, 改进后的算法实时性和适应性更好, 但是该算法仅局限于对缺失数据进行修复, 其他异常情况无法处理; 文献[12]根据传感器数据的时序性特点, 提出了一种基于嵌套滑动窗口的数据缺失填充算法, 通过皮尔逊分析数据项的空间相关性, 然后使用固定大小的嵌套滑动窗口进行数据采样处理, 通过MKNN算法进行缺失数据的精准填补, 该算法的复杂度更低, 数据修复效果精准, 但是也只局限于缺失数据异常问题.
通过对现有数据处理技术的分析, 并不适合应用于流程型制造车间生产数据的处理, 因为其数据种类多, 格式不一, 不同数据项采集频率不一, 数据质量也是参差不齐, 加上不同任务对数据的实时性和准确性要求不同, 所以不能一概而论. 本文根据生产数据特点不同, 将其分为3类: 状态数据、开关数据和逻辑数据. 其中状态数据是生产过程中表示环境、设备运行状态的数据信号, 如物料重量、传送带速度、焙烧温度时间、环境温度湿度等; 开关数据是设备启动、停止, 以及阀门开关时产生的开关信号; 逻辑数据是设备运行中表示是否运行的逻辑信号, 如电流、频率, 其值在某一范围内有效.为了满足流程型车间生产任务的实际需求, 针对不同数据类型, 不同异常类型采用了不同的处理策略.
1 相关定义 1.1 数据模型待处理数据是典型的时间序列[9]数据, 即一系列按时间先后顺序、等间隔采集的数据点所组成的数据序列. 因此, 数据模型可表示为由采集点唯一标识、采集时间以及数据值组成, 记为:
| $ D = \{ {d_1} = ({p_1},{t_1},{v_1}), \cdots ,{d_i} = ({p_i},{t_i},{v_i}), \cdots ,{d_n} = ({p_n},{t_n},{v_n})\} $ |
其中, di=(pi,ti,vi)表示在pi采集点、ti时刻采集的数据值为vi, 并且时间是一维线性递增的, n为时间序列的长度.制造车间所有采集点在环境的影响下采集到的生产数据, 如图1所示

|
图 1 生产数据示意图 |
流程型制造车间生产过程中时间序列数据的特点就是数据维度高, 即数据值v表示的类型众多, 如温度值、速度值、重量值等; 加上时间流特点, 这决定了不能使用传统单一的数据处理方式进行处理. 因此, 降低数据维度、提高数据处理算法效率成为关键. 本文首先根据数据特征, 进行数据分类处理, 再针对每类数据采用适合的算法进行处理, 在保证数据处理质量的前提下, 最大化提高处理效率[13].
1.2 滑动窗口滑动窗口[12]是一个固定长度的队列, 窗口中的数据是过去一段时间内采集数据点组成的数据流. 数据点从窗口首部流入, 尾部流出.
根据窗口中存放数据方式的定义, 滑动窗口分为基于时间的滑动窗口和基于数据个数的滑动窗口; 其中基于时间的滑动窗口保存最近一段时间长度内采集到的数据; 基于数据个数的滑动窗口保存最近采集到的K个数据.
结合采集数据的特点分析, 数据可能存在丢失情况, 如果采用基于时间的定义方式, 则在一定时间段内进入滑动窗口的数据项个数可能很少, 在数据修复时准确度会下降. 所以本文选择基于数据个数的滑动窗口. 在数据处理过程中, 结合生产工艺的具体情况分析, 根据每类数据的特点不同, 为每类数据建立不同宽度的滑动窗口缓存数据, 尽可能实时高效的处理数据.
例如滑动窗口大小N, 在ti时刻, 进入滑动窗口的数据流(d1, d2, ···, dn), 如图2所示[12].

|
图 2 ti时刻滑动窗口 |
在tj时刻, 滑动窗口中前i–j个数据移出窗口, dn+1至dn+i–j作为最新数据进入滑动窗口, 存放在最右位置, 如图3所示.

|
图 3 tj时刻滑动窗口 |
随着时间推移, 数据流不断流入滑动窗口, 窗口中的数据不断更新, 并且每次只需要处理更新后的数据, 即dn+1至dn+i–j.
2 数据流处理算法 2.1 处理模型本文针对流程型制造车间采集数据来源广、采集频率不同、格式不同等特点分析, 提出基于滑动窗口的多源数据分类处理模型. 如图4所示[14].

|
图 4 基于滑动窗口的多源数据分类处理模型 |
首先根据生产管控任务从数据源中选择需要的数据项, 在进行处理前根据数据特点进行分类, 可划分为3类数据, 分别是状态数据、开关数据、逻辑数据; 基于各类数据对完整性、准确性的需求不同, 采用不同的处理算法进行修复; 最后根据生产管控任务中数据项的关联关系将处理后的数据进行多源融合, 方便应用.
2.2 数据分类依据根据数据的采集频率将数据分为3类: 逻辑数据、状态数据、开关数据. 其中逻辑数据变化最频繁, 采样频率最高, 状态数据次之, 开关数据最后; 状态数据包含数据项、异常情况最多, 分析处理也最为复杂. 以下是对不同种类数据进行异常分析处理的过程.
2.3 状态数据状态数据的异常情况可以分为3类: 数据重复、数据离群和数据丢失; 其中丢失数据的修复较为复杂.根据状态数据的特点, 主要采用EM算法进行改进, 结合滑动窗口技术进行处理, 提高数据处理的精度和性能.
(1)重复
根据之前对数据模型的分析, 每个数据点都是由采集点唯一标识、采集时间和采集值构成, 记d1=(p1,t1,v1). 所以重复数据可以根据采集时间的唯一性过滤.
(2)离群
离群数据包括局部异常高值、低值, 超出数据阈值. 其中超出数据阈值异常可以通过为每个数据项配置数据阈值方式过滤; 局部异常高值低值可以通过中值法修复, 如下式:
| $d({p_i},{t_i},{v_i}) = \;\dfrac{{{d}({p_i},{t_{i + 1}},{v_{i + 1}}) + {d}({p_i},{t_{i - 1}},{v_{i - 1}})}}{2}\;\;$ | (1) |
(3)缺失
数据缺失的异常处理较为复杂, 分为连续型缺失和不连续型缺失. 针对不连续缺失情况, 由于缺失数据前后时间间隔较短, 可以采用中值法进行修补; 对于连续型缺失, 由于缺失数据过多若使用中值法修复, 则可能导致误差较大, 所以本文采用改进的EM (Expectation-Maximization algorithm, 最大期望算法)插值法, 处理连续性缺失[10,11]. EM算法是一种从不完整数据集中对参数进行估值, 然后通过不断迭代求参数最大似然值的经典数据修复算法之一.
文献[10]介绍了针对EM算法进行改进处理缺失数据的情况. 改进的EM缺失插补算法有3个特点: (1) 设定连续缺失数据点个数的阈值为M, 当连续缺失数据个数小于M时, 表明数据缺失不严重, 使用中值法进行修复, 大于M时才使用EM插补算法; (2)设定EM算法的最高迭代次数为K, 当算法迭代次数大于K时, 停止迭代, 使用最后一次迭代结果作为缺失数据的插补值; (3)设定算法迭代精度ε, 当第k次与k–1次迭代结果差小于ε时, 表明结果满足要求, 停止迭代, 这样可以在保证数据处理质量的前提下, 提高数据处理效率.
数据修复的整个过程是基于固定大小的滑动窗口模型, 窗口宽度为N, 数据缺失阈值为M, 最高迭代次数为K, 迭代精度为ε, 数据的采样频率为T, 即时间序列数据正常到达滑动窗口的时间间隔. 计算滑动窗口相邻两条数据di=(pi,ti,vi) 和di+1=(pi,ti+1,vi+1)的时间间隔△t=ti+1–ti, 比较△t与M×T的关系, 共有3种情况, 如下:
(1)当△t < 2× T, 则采集数据无缺失情况, 无须处理;
(2)当2×T≤△t≤M×T, 则数据点d1和d2之间存在缺失点, 但没有超过设定的缺失阈值M, 使用中值法进行修复;
(3)当△t≥M×T, 则缺失数据个数超出阈值M, 采用EM算法进行修复. 具体如下[12]: 首先记滑动窗口中N个数据点构成的数据集为S, 假设其中有m个连续缺失的数据点, 记为di(i=1,2,···,m). 扫描数据集, 分别以m个连续缺失数据为中心进行高斯模型划分, 得到m个高斯模型分别记为S1, S2, ···, Sm, 构成高斯混合模型[11], 表示为:
| ${p}({S_i}) = \sum\limits_{i = 1}^m {{\pi _i}({S_i}|{\mu _i},{\varSigma _i})} \;\;$ | (2) |
其中, N(si |μi,
| ${p}({S_i}{\rm{|}}{{Z}_k} = 1) = N({S_i}|{\mu _i},{\varSigma _i})$ | (3) |
在贝叶斯思想下, p(z)是先验概率, p(s|z)是似然概率, 得到后验概率p(z|s)如下:
| $\gamma ({Z_k}) = {p}({Z_k} = 1|{S_{}}) = \frac{{{\pi _i}N({S_{}}|{\mu _i},{\varSigma _i})}}{{\displaystyle\sum\limits_{j = 1}^m {{\pi _i}N(S|{\mu _j},{\varSigma _j})} }}$ | (4) |
为了方便计算模型的参数, 在式(4)中用γ(zk)表示第k个分组的后验概率. 这里有3个参数π, μ,
| ${\mu _{i}} = \frac{1}{{{C_i}}}\sum\limits_{n = 1}^C \gamma ({Z_{ni}}){x_n}$ | (5) |
| $ {\sum _{i}} = \frac{1}{{{C_i}}}\sum\limits_{n = 1}^C \gamma ({Z_{ni}})({x_n}{\rm{ - }}{\mu _{i}}{\rm{)(}}{x_n}{\rm{ - }}{\mu _{i}}{{\rm{)}}^{T}} $ | (6) |
| ${\pi _{i}} = \frac{{{{{C}}_i}}}{C}$ | (7) |
其中, C表示每个分组中包含数据点的个数, xn表示当前分组中的第n个点, γ(zni)表示第n点属于分组Si的后验概率.
然后设定最大迭代次数K, 初始迭代次数K0
求期望: 根据当前πi、μi、
| $\gamma ({{\textit{z}}_n}\;i) = \frac{{{\pi _i}\;N({x_n}\;|\;{\mu _n},{\varSigma _n})}}{{\displaystyle\sum\nolimits_{j = 1}^m {\;{\pi _j}\;N({x_n}\;|\;{\mu _j},{\varSigma _j})} }}$ | (8) |
求极大: 根据求期望步骤可得的γ(zni), 再代入式(5)~式(7)计算πi、μi、
开关数据主要有两种状态开和关, 有两种表现形, 第一种分别用True和False表示开和关, 另一种用1和0表示用开和关, 两种表示形式的数据处理都不复杂. 首先需要将非数字量转换为数字量的0或1; 然后结合生产工艺, 联合相关数据项进行处理, 这里不做详细介绍. 对于同一采集点的开关数据处理结果一定是{0,1,0,1,···}.
2.5 逻辑数据逻辑数据是另一种形式表示设备开关状态的数据, 其采样频率高, 但是只有在一定范围内才有效, 如机器运转的频率、电流、电压等, 只有频率达到某个范围才表示机器在运转中, 而在这个范围内, 数据波动频繁, 有时出现异常情况可能跳出范围内. 所以对该类数据的容错性较高, 即使出现部分数据缺失、离群对整体数据的影响不大, 处理的重点在于找到数据趋于稳定的点, 将稳定在某范围内的数据按逻辑1处理, 其余按逻辑0处理. 这样便于对逻辑数据的分析时找到从0跳变到1或者从1跳变到0的时间点.
本文采用二次稳定度算法判断逻辑数据的稳定性, 具体如算法1[15].
算法1. 二次稳定度算法
1) 结合生产工艺和数据特点, 选择合适的波动率(R1,R2), 其中R1、R2分别是第一次和第二次稳定性判断的波动率, 以及稳定指标(S1,S2); 一般情况下波动率R1大于R2, 稳定指标S1小于S2;
2) 从计算滑动窗口中所有数据的总值Vsum和平均值Vavg; 当每次滑动窗口向后移动时只需要用Vsum减去移出数据值, 再加上移入数据值即可得到新的总值;
3) 根据波动率R1确定均值上下的一次稳定区间[Vavg–Vavg×R1, Vavg+Vavg×R1], 然后计算滑动窗口中数据在一次稳定区间中的概率, 即数值在稳定区间的个数占总数的比值P1; 如果P1小于S1, 则判定数据不稳定, 将滑动窗口首位置为0, 否则执行4);
4) 根据波动率R2计算均值上下的二次稳定区间[Vavg–Vavg×R2, Vavg+Vavg×R2], 然后计算滑动窗口中数据在二次稳定区间中的概率P2; 如果P2大于等于S2,则判定数据稳定, 将滑动窗口首位置为1, 否则置为0.
3 实验结果 3.1 实验环境说明本文采用的实验环境是Windows 7, CPU 3.6 GHz, 内存16 GB的计算机; 实验数据是某锂电池材料生产车间产生的数据, 该生产车间是典型的流程型生产车间, 数据种类多, 质量参差不齐, 采样间隔1 s, 如表1所示.
| 表 1 部分生产数据 |
3.2 实验结果
本文分别选取滑动窗口的宽度N为150, 160, 170, 180, 190, 200; EM算法循环迭代精度ε=0.1; 数据缺失阈值W=4,5,6,7,8; 分别进行实验验证, 最后选定滑动窗口宽度N=180, 数据缺失阈值W=7时数据插补效果最好.
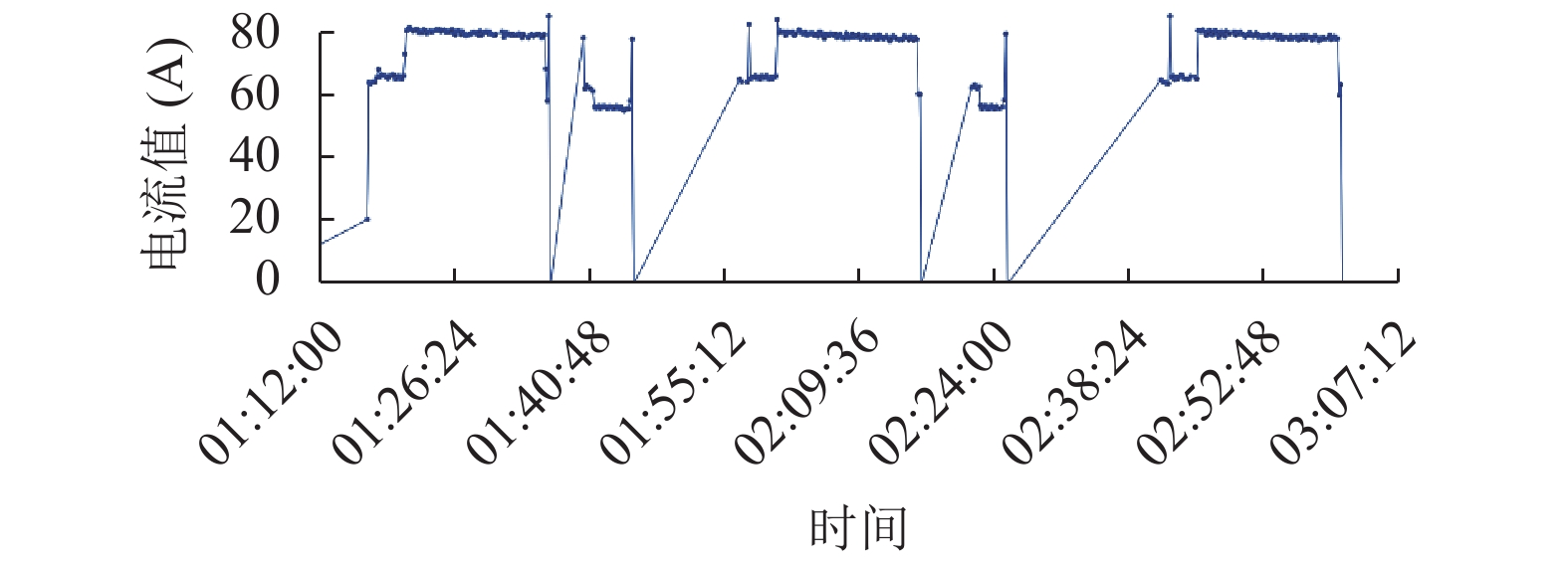
同时对于逻辑数据由于生产环境因素影响造成其值在一定范围内波动的情况, 如图5所示, 为原料高混机运行时产生的电流数据.
|
图 5 高混机电流数据 |
为了便于找到数据稳定趋势, 分析从逻辑0跳变到逻辑1, 或者相反跳变的时间点, 采用二次稳定度算法, 结合生产工艺设置波动率R1、R2分别是10%、5%, 稳定指标S1、S2分别是90%、80%, 将稳定在某范围内的数据值按逻辑1处理, 其余按照逻辑0处理, 结果如图6所示.

|
图 6 处理后的电流数据 |
最后为了验证数据处理效果, 将经过处理后的数据应用于流程型制造车间锂电池材料产品生产批次判断, 与实际人工统计结果比较, 误差率不足1%.
4 结论与展望本文针对流程型车间生产数据的多样性、数据质量参差不齐等问题, 采用数据分类处理技术, 相比与传统的单一数据处理技术, 提高了数据处理效率, 为数据应用于过程控制提供了保障. 最后以某锂电池材料生产车间生产数据为例, 验证了所设计的数据分类处理模型. 结果表明: 该方法在保证数据处理质量的前提下, 较传统数据处理方法更加简洁、高效, 具有实际应用价值.
| [1] |
Ponce LM, dos Santos W, Meira Jr W, et al. Upgrading a high performance computing environment for massive data processing. Journal of Internet Services and Applications, 2019, 10(1): 19. DOI:10.1186/s13174-019-0118-7 |
| [2] |
Van Nguyen T, Zhou L, Chong AYL, et al. Predicting customer demand for remanufactured products: A data-mining approach. European Journal of Operational Research, 2019, 281(3): 543-558. |
| [3] |
Niu G, Yang BS, Pecht M. Development of an optimized condition-based maintenance system by data fusion and reliability-centered maintenance. Reliability Engineering & System Safety, 2010, 95(7): 786-796. |
| [4] |
赵颖, 侯俊杰, 于成龙, 等. 面向生产管控的工业大数据研究及应用. 计算机科学, 2019, 46(S1): 45-51. |
| [5] |
Nardelli M, Cardellini V, Grassi V, et al. Efficient operator placement for distributed data stream processing applications. IEEE Transactions on Parallel and Distributed Systems, 2019, 30(8): 1753-1767. DOI:10.1109/TPDS.2019.2896115 |
| [6] |
Liu TH, Wei HK, Zhang KJ. Wind power prediction with missing data using Gaussian process regression and multiple imputation. Applied Soft Computing, 2018, 71: 905-916. DOI:10.1016/j.asoc.2018.07.027 |
| [7] |
曹原, 刘英博, 肖利, 等. 状态监测数据流时间乱序问题建模与研究. 计算机集成制造系统, 2013, 19(12): 2960-2967. |
| [8] |
程进, 王坚. 数据驱动的流程制造工艺参数匹配方法. 计算机集成制造系统, 2017, 23(11): 2361-2370. |
| [9] |
Wang XY, Mueen A, Ding H, et al. Experimental comparison of representation methods and distance measures for time series data. Data Mining and Knowledge Discovery, 2010, 26(2): 275-309. |
| [10] |
张宙锋, 张磊, 王志超. 改进的数据流缺失数据处理算法. 微电子学与计算机, 2012, 29(3): 55-59. |
| [11] |
王凯南, 金立左. 基于高斯混合模型的EM算法改进与优化. 工业控制计算机, 2017, 30(5): 115-116, 118. DOI:10.3969/j.issn.1001-182X.2017.05.049 |
| [12] |
许江, 陈志奎, 张清辰. 基于嵌套滑动窗口的数据流缺失数据填充算法. 西南师范大学学报(自然科学版), 2015, 40(11): 130-136. |
| [13] |
Liu GY, Yang J, Hao Y, et al. Big data-informed energy efficiency assessment of China industry sectors based on K-means clustering. Journal of Cleaner Production, 2018, 183: 304-314. DOI:10.1016/j.jclepro.2018.02.129 |
| [14] |
徐卫, 朱翔宇, 刘志. 城市多源交通数据分析处理关键技术研究. 浙江工业大学学报, 2018, 46(3): 305-309, 315. DOI:10.3969/j.issn.1006-4303.2018.03.012 |
| [15] |
李娜, 黄孝彬, 田志强, 等. 生产过程数据稳定性判断的一种方法. 华电技术, 2010, 32(1): 32-34, 38. DOI:10.3969/j.issn.1674-1951.2010.01.011 |
 2020, Vol. 29
2020, Vol. 29



