2. 国家电网 国网安徽省电力有限公司 电力科学研究院, 合肥 230601
2. Electric Power Research Institute, State Grid Anhui Electric Power Co. Ltd., State Grid, Hefei 230601, China
配电网网络重构是配电管理系统的重要研究内容, 也是配电网优化运行和控制的有效手段, 它通过开关状态的变化来形成满足优化目标的新网络结构, 使网络负荷分布更加合理[1]. 传统网络重构多以有功网损最小为目标, 但随着人们对供电可靠性的要求越来越高, 配电网的运行需要考虑更多的可靠性因素, 而配电网重构是一个多目标、多约束的复杂非线性规划问题[2], 在配电网重构加入可靠性指标时会进一步加大重构模型求解的复杂度, 为提高配电网运行的可靠性和经济性, 需对计及供电可靠性指标的配电网重构进行系统的深入研究.
网络重构的传统方法有分支定界法和单纯型法等, 传统数学优化法虽然可以得到不依赖于配电网初始结构的全局最优解, 但其只适用于简单结构的配电网, 对于结构较复杂的配电网计算时间过长、效率低下[3]. 近年来, 随着人工智能算法的广泛应用[4], 相关学者将人工智能方法应用到配电网重构中, 取得了不错的效果. 文献[5]采用遗传算法来求解配电网重构模型, 遗传算法虽然具有良好的全局并行处理能力, 搜索效率较高, 但其局部搜索能力较差, 易陷入局部最优解的缺陷. 文献[6]将粒子群算法应用于配电网重构模型的求解, 粒子群算法具有优良的局部搜索能力, 但其全局搜索能力较差, 算法收敛困难. 以上文献的研究均是以单一的配电网有功损耗最小为重构的目标, 未考虑供电可靠性的因素. 文献[7]虽然建立了包括可靠性指标的配电网重构模型, 但其对于多目标的权重处理采用的是层次分析法, 该方法主观性过强.
本文建立了计及供电可靠性指标的配电网多目标优化重构模型, 提出一种改进的人工蜂群算法, 并将其应用于配电网重构模型的求解, 通过建立的配电网实例的重构计算分析对本文重构方法的可行性和优越性进行了验证.
1 计及可靠性指标的配电网重构模型配电网规划时通常采用闭环的形式, 而实际运行则采用开环形式, 节点间存在分段开关, 整个网络有一定的联络开关. 配电网重构是在满足一定约束的条件下, 通过对开关状态的调整来达到减小损耗和提高供电可靠性等目标[8].
1.1 目标函数配电网重构一般以系统有功网损最小为目标, 未考虑配电网的供电可靠性, 本文以配电网有功网损最小和供电可靠性指标最优为共同目标.
配电网有功网损计算表达式为:
| ${P_L} = \sum\limits_{i = 1}^L {{k_i}} {R_i}\frac{{P_i^2 + Q_i^2}}{{U_i^2}}\;\;\;$ | (1) |
其中, L表示配电网支路总数, ki为支路i的开关状态变量, 1为闭合、0为断开, Pi、Qi、Ri、Ui为支路i的有功、无功、电阻及节点电压大小.
配电网可靠性指标包括系统可靠性指标和负荷点可靠性指标[9], 负荷点可靠性指标表示的是网络结构对某一负荷点可靠性的影响, 而系统可靠性指标则能全面地反映在某种结构下的可靠性优劣. 因此, 对配电网供电可靠性进行评估时选取系统可靠性指标能更好地反映网络的可靠性. SAIFI(系统平均停电频率)和CAIFI(用户平均断电频率), SAIDI(系统平均停电持续时间)和CAIDI(用户平均停电持续时间), ASAI(平均供电可用率)和AENS(系统供电量不足)这3对指标描述的均是同一问题的两个方面, 且3对指标是相互关联的, 任意两类指标均可反映出其它两类, 对系统可靠性指标进行综合考虑后, 本文选取SAIFI和SAIDI作为重构模型中考虑的网络可靠性因素, 计算公式为:
| $SAIFI = \frac{{{\text{用户总停电次数}}}}{{{\text{总用户数}}}}{\rm{ = }}\frac{{\displaystyle \sum {{\lambda _i}{N_i}} }}{{\displaystyle \sum {{N_i}} }}$ | (2) |
| $SAIDI = \frac{{{\text{用户停电持续时间总和}}}}{{{\text{总用户数}}}}{\rm{ = }}\frac{{\displaystyle \sum {{T_i}{N_i}} }}{{\displaystyle \sum {{N_i}} }}$ | (3) |
其中, λi表示负荷点i的故障率, Ni表示用户数, Ti表示年平均停电时间.
本文配电网重构模型目标函数表达式如下所示:
| $F = ({f_1},{f_2},{f_3}) = \min({P_L},SAIFI,SAIDI)$ | (4) |
配电网重构的数学模型还需满足一定的等式约束条件和不等式约束条件.
等式约束条件指配电网系统的潮流需满足功率平衡的等式约束.
| ${P_{{\rm{G}}i}} - {U_i}\sum\limits_{j \in i} {{U_j}\left( {{G_{ij}}\cos {\delta _{ij}} + {B_{ij}}\sin {\delta _{ij}}} \right)} - {P_{{{L}}i}} = 0$ | (5) |
| ${Q_{{\rm{G}}i}} - {U_i}\sum\limits_{j \in i} {{U_j}({G_{ij}}\sin{\delta _{ij}} - {B_{ij}}\cos{\delta _{ij}})} - {Q_{{{L}}i}} = 0$ | (6) |
其中, PGi、PLi、QGi、QLi为节点i电源和负荷的有功功率、无功功率, Ui、Uj为电压幅值大小; δij、Gij、Bij为相角、电导和电纳值.
不等式约束包括节点电压约束、支路电流约束和网络拓扑约束.
| $U_i^{\min } \le {U_i} \le U_i^{\max }$ | (7) |
| ${I_l} \le I_l^{\max }$ | (8) |
| ${g_k} \in {G_k}$ | (9) |
其中,
人工蜂群算法是由Karaboga于2005年提出的一种模拟自然界蜜蜂采蜜过程的群体智能算法[10]. 人工蜂群包括雇佣蜂、观察蜂和侦察蜂, 雇佣蜂负责搜索食物源及其邻域, 并将食物源的相关信息传递给观察蜂, 观察蜂再综合相关信息决定一个食物源目标进行搜索, 若经过规定的搜索次数后, 雇佣蜂未寻到更优的食物源, 则雇佣峰转变成侦察蜂, 并随机寻找新的食物源, 食物源的位置集为优化问题的解集, 食物源对应的花蜜量则为解的适应度. 人工蜂群算法具有鲁棒性强、通用性好和收敛效率快等优良特性, 但其仍存在着局部开采能力差和易陷入“早熟”的缺陷[11]. 因此, 为进一步提高人工蜂群算法的优化求解能力, 本文对其进行相应的改进, 本文将量子理论引入到算法中, 并在迭代的过程中将Metropolis准则来取舍最优解.
蜜蜂的位置由一串量子位表示, 第k只蜜蜂的量子位置为:
| ${v_k} = \left[ {\begin{array}{*{20}{c}} {{\alpha _{k1}}}&{{\alpha _{k2}}}&\cdots&{{\alpha _{kl}}} \\ {{\beta _{k1}}}&{{\beta _{k2}}}&\cdots&{{\beta _{kl}}} \end{array}} \right]$ | (10) |
其中, α、β满足
蜂群的进化主要由蜜蜂的位置更新来实现, 第k只蜜蜂位置的第i个量子位vki为:
| $v_{ki}^{t + 1} = {\rm{abs}}(U(\theta _{ki}^{t + 1})v_{ki}^t)$ | (11) |
| $U(\theta _{ki}^{t{\rm{ + 1}}}) = \left[ {\begin{array}{*{20}{c}} {\cos \theta _{ki}^{t{\rm{ + 1}}}}&{ - \sin \theta _{ki}^{t{\rm{ + 1}}}} \\ {\sin \theta _{ki}^{t{\rm{ + 1}}}}&{\cos \theta _{ki}^{t{\rm{ + 1}}}} \end{array}} \right]$ | (12) |
其中,
若
| $v_{ki}^{t + 1} = \overline N v_{ki}^t = \left[ {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right]v_{ki}^t$ | (13) |
量子人工蜂群主要由工蜂和观察蜂组成, 蜜蜂位置对应的食物源为一个由0或1数字串, 食物源k的位置为:
| $x_{kd}^{t + 1} = \left\{ \begin{array}{l} 1,\;\;\eta _{kd}^{t + 1} > {(a_{kd}^{t + 1})^{\rm{2}}} \\ {\rm{0,}}\;\;\eta _{kd}^{t + 1} \le {(a_{kd}^{t + 1})^{\rm{2}}} \\ \end{array} \right.$ | (14) |
式中,
设蜜蜂的局部最优位置为: pk=(pk1, pk2, ···, pkl), 蜂群当前的全局最优位置为: pg=(pg1, pg2, ···, pgl).
工蜂位置更新表达式为:
| $\theta _{id}^{t + 1} = {e_1}(p_{id}^t - x_{id}^t) + {e_2}(p_{gd}^t - x_{id}^t)$ | (15) |
| $v_{id}^{t + 1} = \left\{ \begin{array}{l} \overline N v_{id}^t,\;\;{\text{若}}\theta _{id}^{t + 1}{\rm{ = 0}}{\text{且}}\gamma _{id}^{t + 1} < {c_1}\\ {\rm{abs}}[U(\theta _{id}^{t + 1})v_{id}^t],\;\;{\text{其他}} \end{array} \right.$ | (16) |
其中, e1、e2表示影响因子,
观察蜂量子位的进化表达式为:
| $ \theta _{jd}^{t + 1} = {e_3}\left( {p_{id}^t - x_{jd}^t} \right) + {e_4}\left( {p_{jd}^t - x_{jd}^t} \right) + {e_5}\left( {p_{gd}^t - x_{jd}^t} \right) $ | (17) |
| $v_{jd}^{t + 1} = \left\{ \begin{array}{l} \overline N v_{jd}^t,\;\;{\text{若}}\theta _{jd}^{t + 1}{\rm{ = 0}}{\text{且}}\gamma _{jd}^{t + 1} < {c_{\rm{2}}}\\ {\rm{abs}}[U(\theta _{jd}^{t + 1})v_{jd}^t],\;\;{\text{其他}} \end{array} \right.$ | (18) |
其中,
在求解过程中, 采用Metropolis准则来取舍获得的最优解[12]. 如果获得的最优解更优, 则接受它; 否则则根据下式进行判断是否接受.
| ${Q_{i + 1}} = \left\{ {\begin{array}{l} {1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;fit({x_{i + 1}}) < fit({x_i})} \\ {\min [1,1 - Z] > K\;\;fit({x_{i + 1}}) \ge fit({x_i})} \end{array}} \right.$ | (19) |
| $Z = \exp (\left( {fit({x_{i + 1}}) - fit({x_i})} \right)/fit({x_i}))$ | (20) |
| ${x_{i + 1}} = \alpha \times {x_i}$ | (21) |
其中, K为[0, 1]区间的判定阈值, Q(xi+1)表示在状态xi+1下的接受概率, α表示温度冷却系数.
2.2 改进蜂群算法性能检验为验证本文改进后人工蜂群算法的寻优性能, 采用Shubert函数进行相应的测试, 并与遗传、粒子群和改进前的人工蜂群算法进行相应的对比分析. Shubert函数得表达式为:
| $\begin{array}{l} f\left( {x,y} \right) = \left\{ {\displaystyle \sum\limits_{i = 1}^5 {i\cos \left[ {\left( {i + 1} \right)x + i} \right]} } \right\}\left\{ {\displaystyle \sum\limits_{i = 1}^5 {i\cos \left[ {\left( {i + 1} \right)y + i} \right]} } \right\} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+0.5\left[ {{{\left( {x + 1.425\;13} \right)}^2} + {{\left( {y + 0.800\;32} \right)}^2}} \right] \end{array} $ | (22) |
其中, −10 ≤ x, y ≤ 10, 该函数的局部最小值有760个, 全局最优解只有1个(−1.42513, −0.80032), 函数值为−186.730 90. 四种优化算法的种群个体数均为100, 最大迭代步数为10000, 分别进行20次寻优试验, 结果如表1所示.
| 表 1 函数寻优结果分析 |
由表1可知, 本文改进后的人工蜂群算法具有更加优异的寻优性能, 优化结果的平均值和平均收敛时间均是四种算法中最小的, 本文采用量子位的概率幅对蜂群算法中食物源进行编码, 通过量子旋转门相位的旋转实现蜂群算法搜索过程中的食物源更新, 扩展了对解空间的遍历性, 采用量子非门来实现搜索过程的变异操作, 可增加种群的多样性, 可有效扩展全局最优解的数量, 提高获得全局最优解的概率, 另外, 本文采用的Metropolis迭代终止准则, 可概率性地跳出当前局部最优解的陷阱, 使得算法全局性更强, 迭代终止阈值的设置则主要根据精度和时间要求进行设定, 精度要求越高, 则阈值越小, 时间要求越快, 则阈值需设定的越大. 为验证不同个体数量对算法性能的影响, 在不同个体数量下进行分别20次寻优, 结果如图1所示.
由图1可知, 随着个体数量的增加, 优化结果随之变优, 当个体数量达到一定程度时, 结果趋于平稳, 但优化时间却明显增加, 因此在设置改进人工蜂群算法个体数量时, 需根据需优化变量个数、结果精度和时间要求进行综合评估.
2.3 配电网重构模型的优化求解本文配电网重构模型是一个多目标优化问题, 多目标优化问题不存在最优解, 而是由许多非劣解构成的Pareto最优解集[13]. 本文通过模糊满意度决策方法来确定最终解, 定义模糊隶属度函数如下:
| ${\mu _j} = \left\{ \begin{array}{l} 1,\;\;\;{f_j} \le f_j^{\min } \\ \dfrac{{f_j^{\max } - {f_j}}}{{f_j^{\max } - f_j^{\min }}},\;\;\;f_j^{\min } \le {f_j} \le f_j^{\max } \\ 0,\;\;\;{f_j} \ge f_j^{\max } \\ \end{array} \right.$ | (23) |
式中, fj、

|
图 1 不同个体数量下优化结果 |
再由下式求取每个目标函数的综合隶属度U, 然后选择U最大的来作为重构模型的折衷解.
| $ U = \sum\limits_{j = 1}^J {{\mu _j}} $ | (24) |
假设本文多目标优化问题的Pareto最优解集为[xi, yi, zi], i=1, 2, ···, N, N为解集的组数, [x1, x2,···, xN]为对应子目标函数f1的解集, 其最小值为xmin, [y1, y2, ···, yN]为对应子目标函数f2的解集, 其最小值为ymin, [z1, z2, ···, zN]为对应子目标函数f3的解集, 其最小值为zmin, 多目标优化问题的理想最优解为[xmin, ymin, zmin]. 综合隶属度U表示解集中任一组解与理想最优解的接近程度, U越大, 则越接近, U ≤ 3, 当U为3时, 表示[xi, yi, zi]为理想最优解.
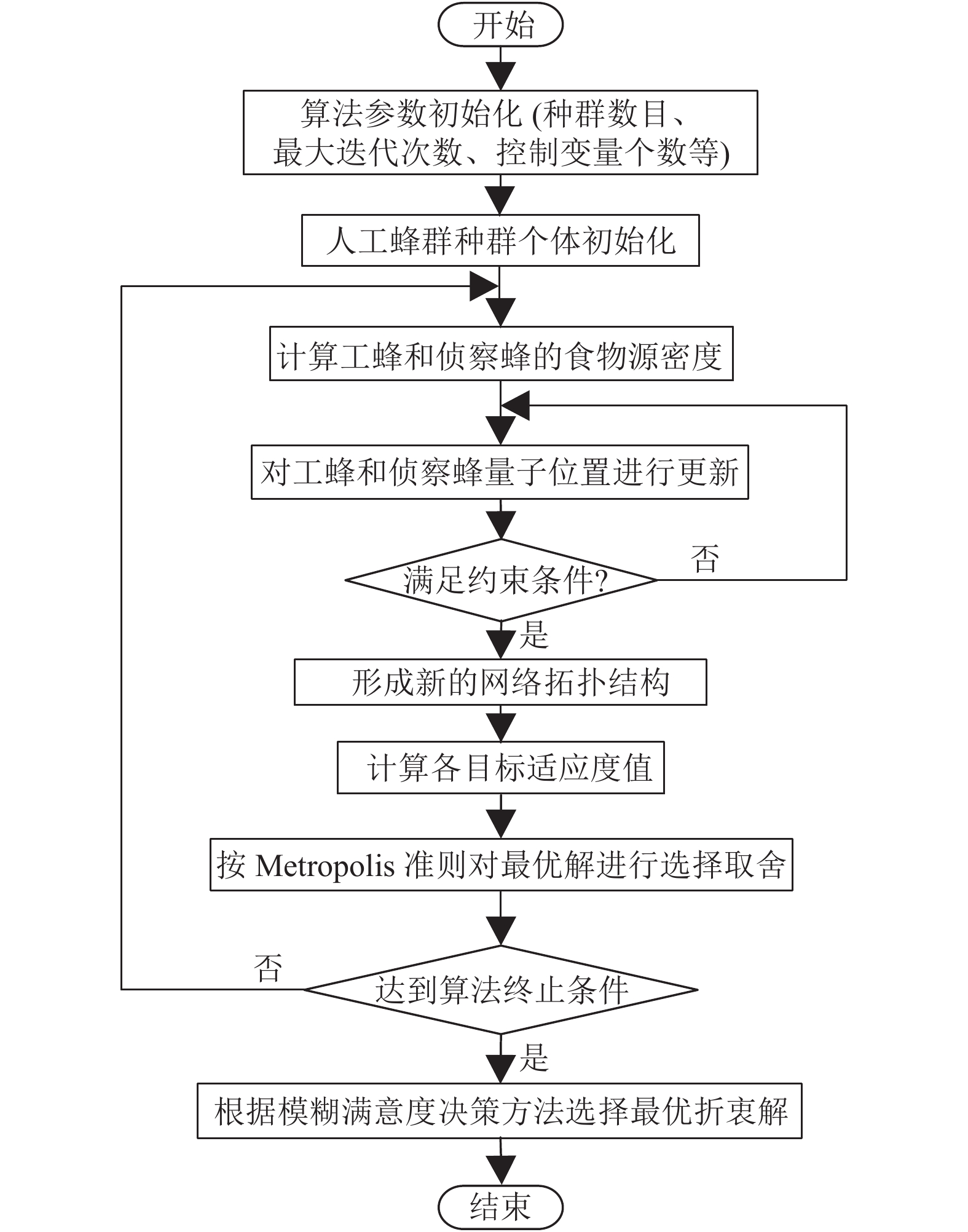
本文利用改进后的人工蜂群算法来对配电网重构多目标问题进行求解, 求解流程图如图2所示.
|
图 2 本文求解基本流程图 |
3 配电网重构实例分析 3.1 系统实例分析
本文以IEEE33节点配电系统为例进行配电网重构分析, 系统结构图如图3所示, 共包含33个节点和37条支路, 分段开关共32个, 联络开关共5个, 配电网支路参数与节点负荷参数见文献[14], 系统基准电压为12.66 kV, 基准功率值为10 MVA, 总负荷为3715 kW+j2300 kvar.

|
图 3 IEEE-33节点系统图 |
3.2 配电网重构结果对比分析
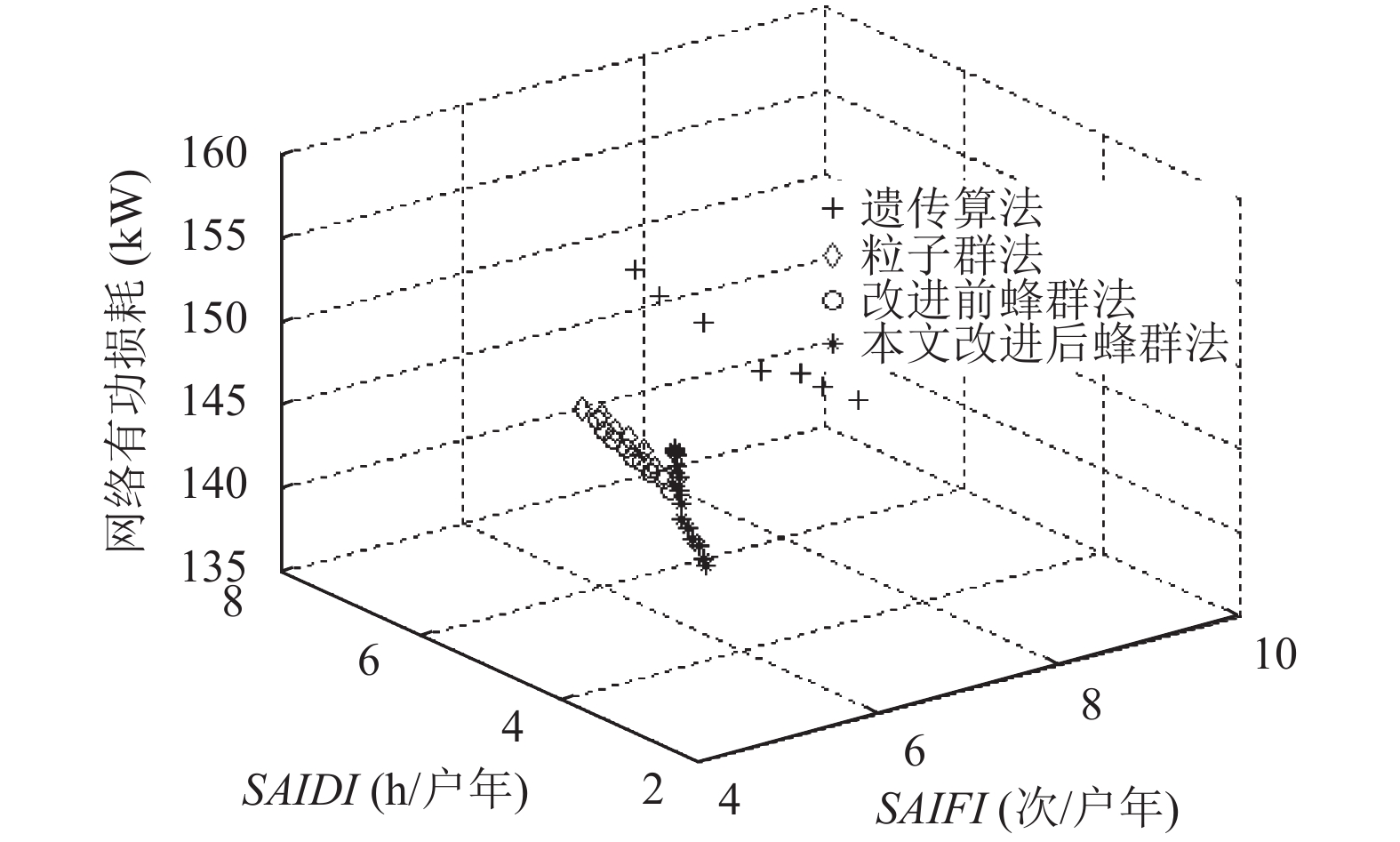
根据本文建立的计及可靠性指标的配电网多目标重构模型, 将本文改进后的蜂群算法应用于模型的求解, 并与遗传、粒子群和改进前的蜂群3种智能算法进行对比分析, 其中配电网可靠性的计算采用故障模式与后果分析法(FEMA), 该方法具有概念清晰、结果准确的优点[15], 在配电网供电可靠性计算中获得广泛应用. 四种不同智能方法优化获得的Pareto前沿如图4所示.
|
图 4 不同方法获得的Pareto最优解前沿 |
由图4可知, 遗传算法、粒子群法、改进前蜂群法和本文改进后蜂群法计算后获得的Pareto最优解个数分别为7、7、9、15, 表明本文改进后蜂群法获得在配电网多目标重构模型求解中获得的Pareto最优解集分布更为完整, 本文算法在寻找最优解的性能上优于其它3种算法.
通过本文2.2小节的模糊满意度决策方法确定4种智能优化方法的折衷最优解如表2所示, 各优化方法优化过程对应的收敛曲线图如图5所示.
根据表2和图5的结果可知, 本文改进后的人工蜂群算法在求解计及可靠性指标的多目标重构模型中拥有更好的优化效果与收敛速度, 优化后选择的Pareto最优解是最优异的: 配电网损耗最小(139.63 kW), 系统平均停电频率SAIFI (5.89次/户年)和系统平均停电持续时间SAIDI (4.35 h/户年)也均是最小的, 且本文方法收敛特性良好, 收敛时间较短(5.69 s). 若在配电网重构时只考虑配电网有功损耗, 采用本文改进后的人工蜂群算法优化得到的配电网损耗虽然更小(137.86 kW), 但重构后的配电网可靠性却大幅下降(SAIFI为8.03次/户年, SAIDI为5.12 h/户年), 严重影响了配电网的安全可靠运行. 因此, 本文计及供电可靠性指标的配电网多目标重构模型能更好地兼顾经济性与可靠性, 更适合配电网的实际运行状况.
| 表 2 重构模型优化结果分析 |

|
图 5 优化过程收敛曲线图 |
4 结论与展望
本文建立了计及供电可靠性指标的配电网多目标重构模型, 多目标的处理采用模糊满意度的决策方法, 并提出了基于改进人工蜂群算法的配电网多目标重构模型优化方法, 通过建立的IEEE33节点配电网实例仿真系统的重构对比分析, 结果表明本文改进后的人工蜂群算法在解决计及可靠性指标的配电网多目标重构中具有更加优越的性能, 获得的Pareto最优解集分布更为完整, 选择的Pareto最优解是最优的: 配电网损耗最小、系统平均停电频率和系统平均停电持续时间也均是最小的, 且本文方法收敛特性良好, 收敛时间较短. 本文计及供电可靠性指标的配电网多目标重构模型能更好地兼顾经济性与可靠性, 在配电网的运行中具有更好的适用性.
| [1] |
杨凯峰, 王击. 配电网络重构算法综述. 南方电网技术, 2013, 7(4): 103-107. DOI:10.3969/j.issn.1674-0629.2013.04.022 |
| [2] |
Shu DS, Huang ZX, Li JY, et al. Application of multi-agent particle swarm algorithm in distribution network reconfiguration. Chinese Journal of Electronics, 2016, 25(6): 1179-1185. DOI:10.1049/cje.2016.10.015 |
| [3] |
董思兵. 基于免疫二进制粒子群算法的配电网重构[硕士学位论文]. 济南: 山东大学, 2008.
|
| [4] |
Zhang FY, Dong YQ, Zhang KQ. A novel combined model based on an artificial intelligence algorithm-a case study on wind speed forecasting in Penglai, China. Sustainability, 2016, 8(6): 555. DOI:10.3390/su8060555 |
| [5] |
胡雯, 孙云莲, 张巍. 基于改进的自适应遗传算法的智能配电网重构研究. 电力系统保护与控制, 2013, 41(23): 85-90. DOI:10.7667/j.issn.1674-3415.2013.23.014 |
| [6] |
马草原, 孙展展, 葛森, 等. 改进二进制粒子群算法在配电网重构中的应用. 电测与仪表, 2016, 53(7): 84-88, 94. DOI:10.3969/j.issn.1001-1390.2016.07.015 |
| [7] |
何禹清, 刘定国, 曾超, 等. 计及可靠性的配电网重构模型及其分阶段算法. 电力系统自动化, 2011, 35(17): 56-60. |
| [8] |
文娟, 谭阳红, 雷可君. 基于量子粒子群算法多目标优化的配电网动态重构. 电力系统保护与控制, 2015, 43(16): 73-78. DOI:10.7667/j.issn.1674-3415.2015.16.011 |
| [9] |
董雷, 何林, 蒲天骄. 中性点接地方式对配电网可靠性的影响. 电力系统保护与控制, 2013, 41(1): 96-101. DOI:10.7667/j.issn.1674-3415.2013.01.015 |
| [10] |
Bansal JC, Sharma H, Arya KV, et al. Memetic search in artificial bee colony algorithm. Soft Computing, 2013, 17(10): 1911-1928. DOI:10.1007/s00500-013-1032-8 |
| [11] |
刘三阳, 张平, 朱明敏. 基于局部搜索的人工蜂群算法. 控制与决策, 2014, 29(1): 123-128. |
| [12] |
Norouzi N, Sadegh-Amalnick M, Tavakkoli-Moghaddam R. A time-dependent vehicle routing problem solved by improved simulated annealing. Proceedings of the Romanian Academy, 2015, 16(3): 458-465. |
| [13] |
戚建文, 任建文, 翟俊义. 基于改进多目标引力搜索算法的电力系统环境经济调度. 电测与仪表, 2016, 53(18): 80-86. DOI:10.3969/j.issn.1001-1390.2016.18.015 |
| [14] |
Su HS, Yang J. Capacitors optimization placement in distribution systems based on improved seeker optimization algorithm. Sensors & Transducers, 2013, 155(8): 180-187. |
| [15] |
王乐. 厦门配电网可靠性提升措施的研究与应用[硕士学位论文]. 广州: 华南理工大学, 2014.
|
 2020, Vol. 29
2020, Vol. 29


