聚类是将数据集中的样本划分为若干个通常不相交的子集, 每个子集称为“族”, 同一族中的对象具有较高的相似度, 不同族中的对象差别较大. 聚类分析已成为数据挖掘领域的研究热点问题, K均值算法(K-means)是一种经典的聚类算法, 因其受初始聚类中心的影响容易陷入局部最优等缺陷而限制了其应用范围. 许多学者提出一系列智能聚类算法, 如蜜蜂交配优化聚类算法[1]、萤火虫聚类算法[2]、差分进化聚类算法[3]、布谷鸟聚类算法[4]、弹性网络聚类算法[5]、花朵授粉聚类算法[6]、蝙蝠聚类算法[7]、灰狼与郊狼混合优化算法[8]、自适应细菌觅食聚类优化算法[9]、拓展差异度的高维数据聚类算法[10]、无人仓系统订单分批问题及K-max 聚类算法[11]等. 各种改进算法均取得了一定成效, 但对于一些复杂问题仍存在精度不高和收敛速度慢等问题.
蝴蝶优化算法[12](Butterfly Optimization Algorithm, BOA)是2018年Sankalap Arora提出一种新的全局优化算法, 其灵感来自于蝴蝶的觅食行为. 该行为由蝴蝶的合作向食物来源位置移动, 蝴蝶接收并感知空气中的气味以确定食物来源或交配伙伴的潜在方向, 但其本质不同于文献[13, 14]. 由于提出时间短, 国外可参考的文献很少, 国内暂无相关论文报道. 蝴蝶优化算法与其他群智能算法一样, 也存在收敛速度和易陷入局部最优等缺陷, 因此本文尝试提出了一种改进蝴蝶优化算法(Improved Butterfly Optimization Algorithm, IBOA), 首先描述了蝴蝶优化算法的特点及实施步骤, 重新定义蝴蝶优化算法的局部迭代公式, 再将遗传算法的轮盘赌选择、交叉操作和变异操作融入蝴蝶优化算法中, 通过标准的数据集测试验证IBOA算法的有效性.
1 基本的蝴蝶优化算法蝴蝶优化算法是模拟蝴蝶的觅食行为, 该思想的条件假设如下:
1) 所有的蝴蝶都应该散发出某种香味, 使蝴蝶能够互相吸引.
2) 每只蝴蝶都会随机移动, 或朝着散发出更多香味的最佳蝴蝶移动.
3) 蝴蝶的刺激强度受目标函数值的影响或决定.
当蝴蝶能感觉到其他任何蝴蝶的香味时并朝它移动, 在该算法中, 该阶段称为全局搜索. 在另一种情况下, 当蝴蝶不能感觉周围的香味时, 然后它会随机移动这个阶段称为局部搜索. 利用转换概率 控制全局和局部搜索过程, 其迭代公式为:
| $ f = {c^t}{I^a} $ | (1) |
| ${x_i^{t + 1} = x_i^t + \left( {{r^2} \times {g^*} - x_i^t} \right) \times {f_i}}$ | (2) |
| ${x_i^{t + 1} = x_i^t + \left( {{r^2} \times x_j^t - x_k^t} \right) \times {f_i}}$ | (3) |
| ${{{{c}}^{{{t + 1}}}} = {{{c}}^{{t}}} + \left( {{{b}}/{{{c}}^{{t}}} \times Ngen} \right)}$ | (4) |
式(1)中的
基于上述描述, 蝴蝶优化算法的实施步骤如下:
Step 1. 初始化种群规模
Step 2. 利用式(5)计算每只蝴蝶的适应度值, 并求出当前最优值fmin和最优解Best.
Step 3. 利用式(1)计算香味感知量, 如果rand<p, 则利用式(2)计算
Step 4. 利用式(5)重新计算每只蝴蝶的适应度值Fnew, if Fnew<fmin, 则替换之前的最优值和最优解.
Step 5. 利用式(4)更新
Step 6. 判断是否达到最大迭代次数, 如果是输出最优值和最优解, 否则跳至Step 3.
2 改进的蝴蝶优化算法由于基本的BOA算法聚类效果差, 本文对其进行改进, 提出一种改进的蝴蝶优化聚类算法. 重新定义蝴蝶的局部搜索方式, 同时结合轮盘赌选择、交叉操作和变异操作, 提高算法的寻优能力, 使聚类效果稳定.
2.1 编码方法采用实数编码, 一只蝴蝶的位置表示一组聚类中心, 假设有
本文采用如下的聚类准则作为适应度值:
| $f({x_i}(t)) = \min \sum\limits_{i = 1}^{{n_c}} {\sum\limits_{j = 1}^m {||{y_i} - {c_j}(t)||} } $ | (5) |
其中,
鉴于基本的蝴蝶优化算法局部寻优能力较差, 故结合精英策略将式(3)重新定义如下:
| $x_i^{t + 1} = x_i^t + r \times (x_j^t - x_k^t) + r \times ({g^ * } - x_i^t)$ | (6) |
式(6)中
为了提高聚类效果和鲁棒性, 融合遗传算法相关操作.
2.4 轮盘赌选择1) 计算每只蝴蝶的适应度值Fitness;
2) 计算每只蝴蝶被遗传到下一代的概率p;
3) 计算每只蝴蝶的累加概率q;
4) 在蝴蝶种群中对每一个体产生一个随机数
1) 在蝴蝶种群中随机选择两个父类
2) 若r<pc, 随机产生一个交叉点point;
3)
设
IBOA算法求解聚类问题的步骤:
Step 1. 初始化种群规模、转换概率、迭代次数N_iter和交叉概率pc等参数.
Step 2. 计算每只蝴蝶的适应度值, 并求出当前最优值fmin和最优解Best.
Step 3. 利用式(1)计算香味感知量, 如果rand<p, 则利用式(2)计算, 否则利用式(6)计算.
Step 4. 重新计算每只蝴蝶的适应度值Fnew, if Fnew<fmin, 则替换之前的最优值和最优解.
Step 5. 执行轮盘赌选择、交叉操作和变异操作. 重新计算每只蝴蝶的适应度值Fnew, if Fnew<fmin, 则替换之前的最优值和最优解.
Step 6. 利用式(4)更新.
Step 7. 判断是否达到最大迭代次数, 如果是输出最优值和最优解, 否则跳至Step 3.
3 实验分析 3.1 实验环境与参数设置为了测试IBOA算法的正确性与有效性, 选取6个基准测试函数来验证算法, 包括1个人工数据集和5个从UCI (
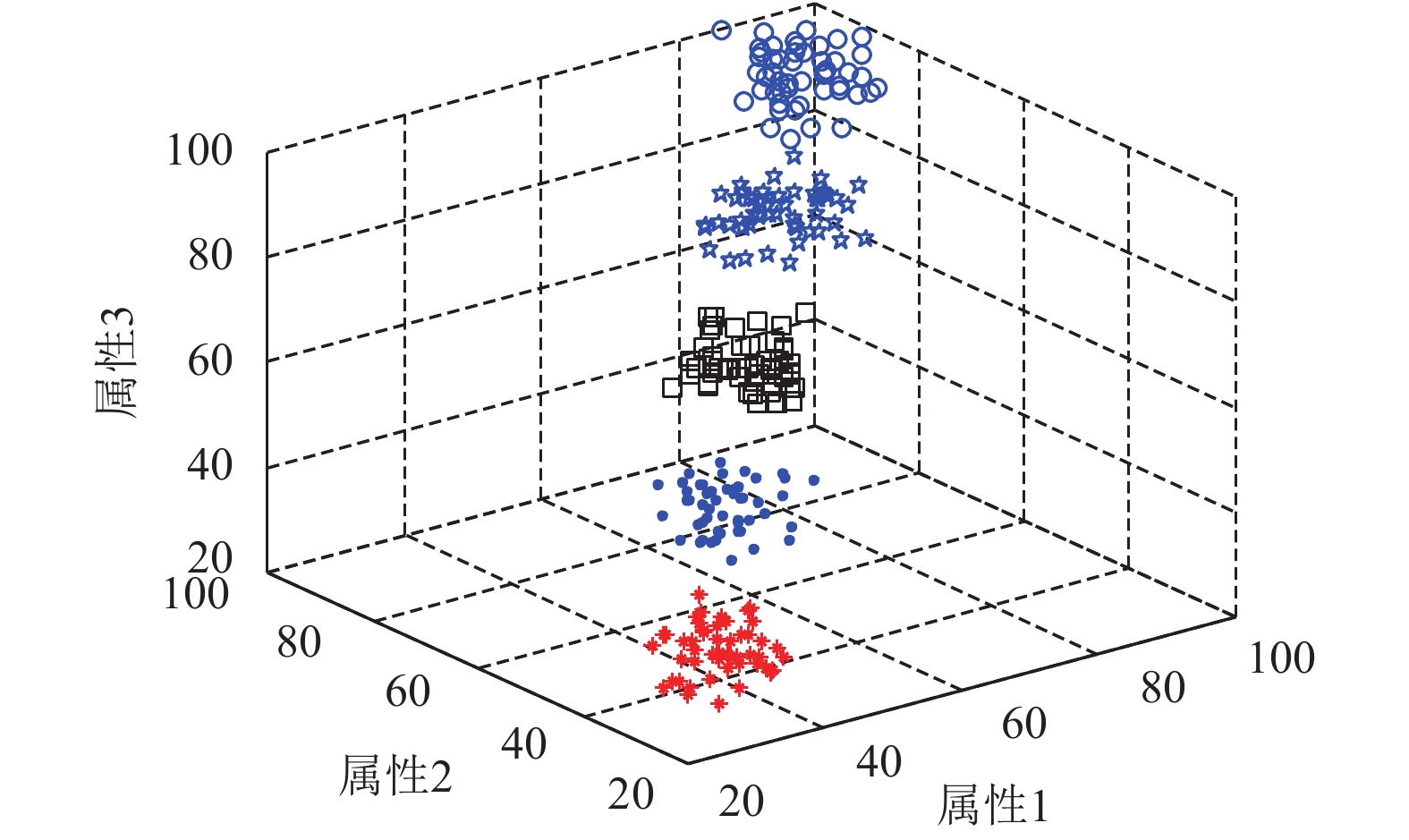
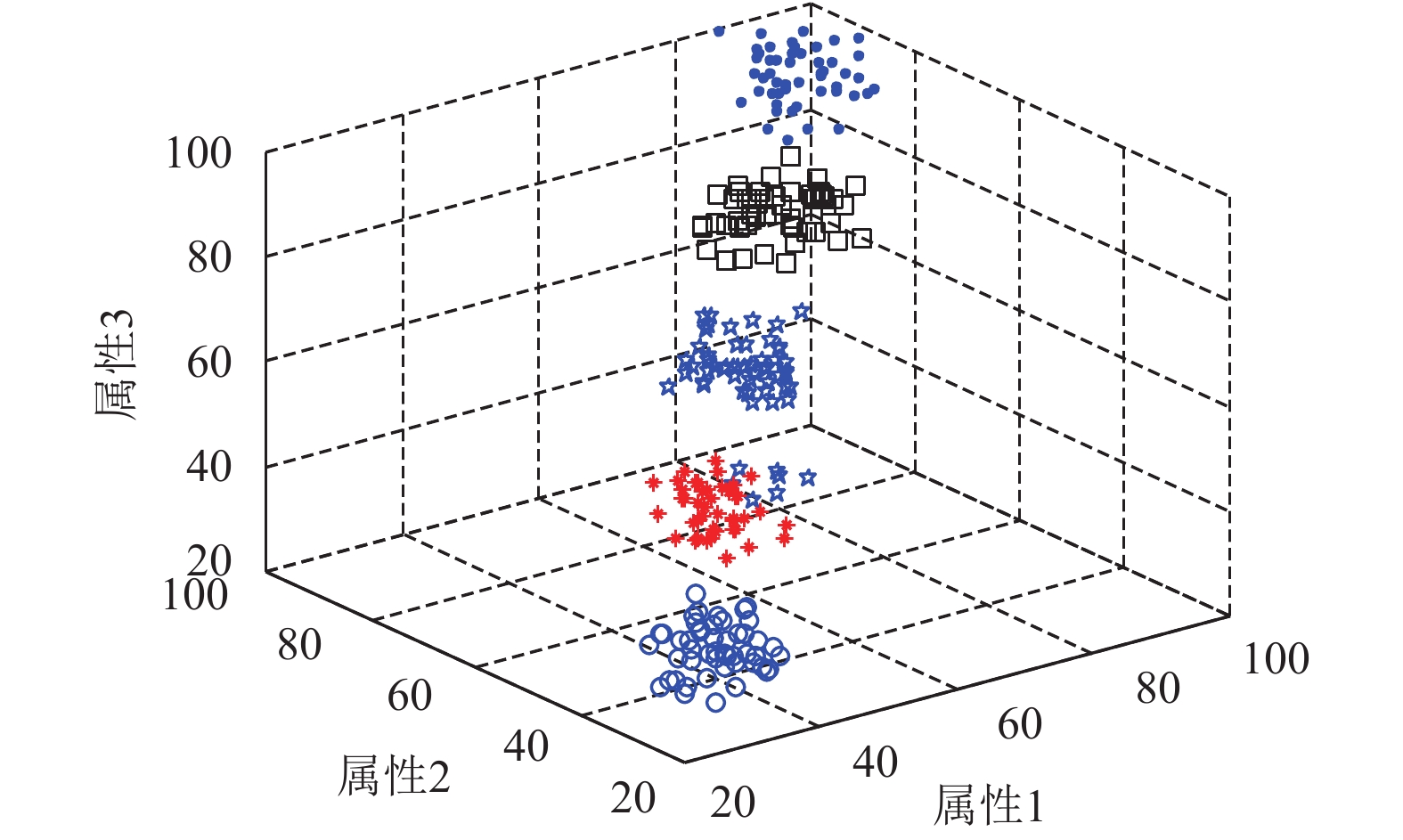
(1)人工数据集1 (set_data=250, d=3, K=5): 为了展示IBOA的求解过程, 分别计算第10代、第50代的求解结果如图1和图2中. 并将算法独立运行20次的结果于表1中, Best表示最优解, Average表示平均解, Worst表示最差解, Std表示标准差.表1中其他算法与数据来源于文献[7], 从表1中的计算结果可知IBOA的求解精度及鲁棒性均优于其他算法.
|
图 1 人工数据集1第10代的聚类结果 |
|
图 2 人工数据集1第50代的聚类结果 |
| 表 1 人工数据集1的20次独立运行结果比较 |
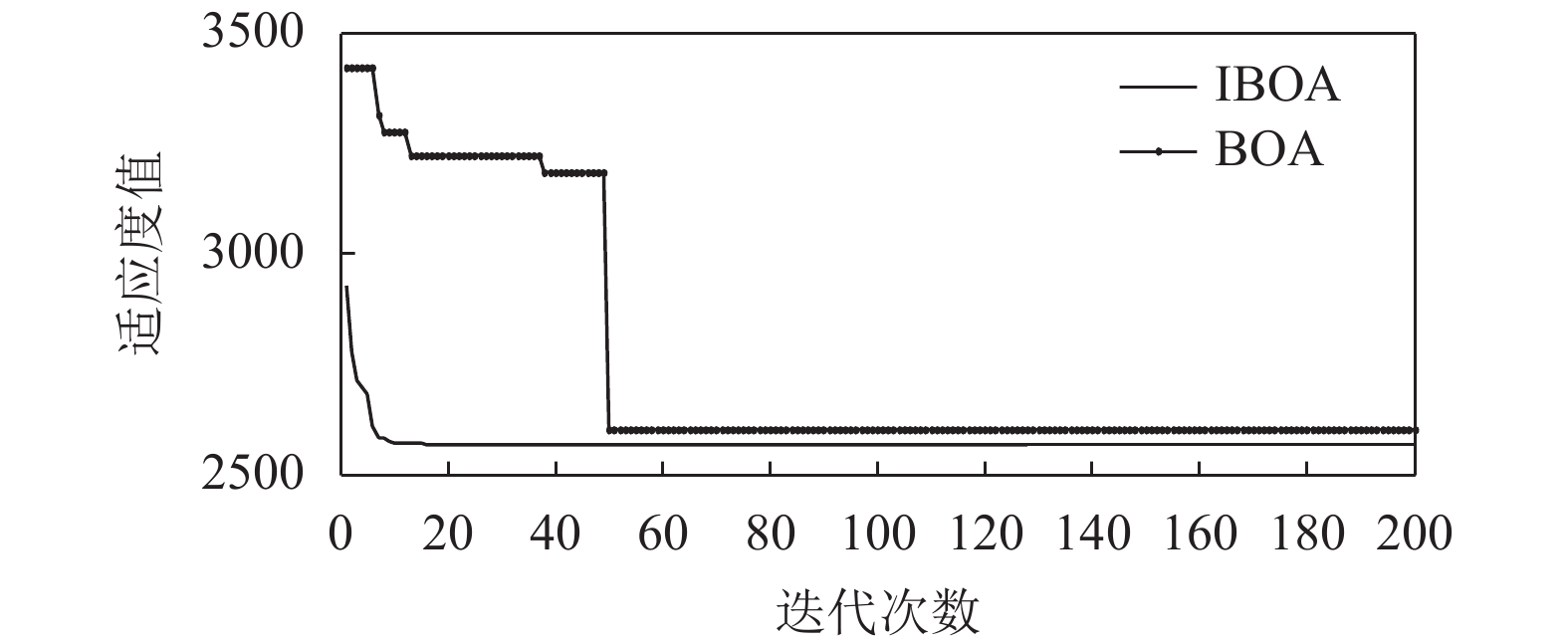
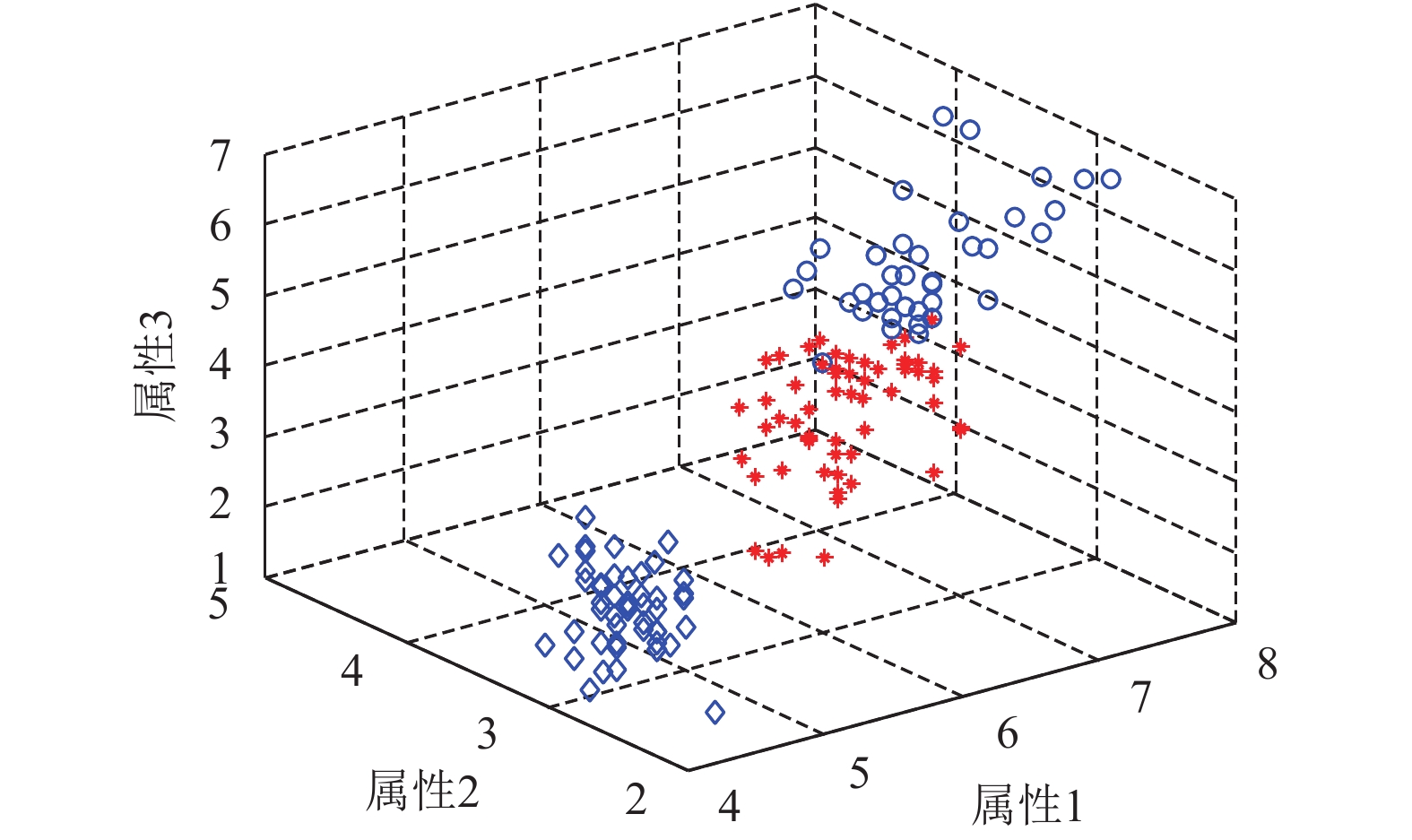
(2)UCI数据集: 将算法独立运行20次, 与近几年多种算法比较如表2–表7所示, 其中表2–表6中的K-means、GA、ACO、PSO、HBMO、IDE算法数据来源于文献[3]且迭代次数为500时的计算结果, IBA算法数据来源于文献[7], IGSO算法数据来源于文献[2], BPFPA算法数据来源于文献[6]; 表7中K-means、PSO、ABC、BA和IBA算法数据来源于文献[7]. 从表2可知, IBOA算法求解效果与IBA、BPFPA相当, 但比其余8种算法效果较好; 从表3可知, IBOA算法与BPFPA求解效果相当, 但比其余7种算法效果优越许多; 文中的“-”表示未有相关数据. 从表4可知, IBOA的求结果在迭代次数为200时优于IDE和其他算法; 从表5可知, IBOA算法的精度和方差均优于其他算法; 从表6可知, IBOA算法的求解效果差于IDE, 与IBA、BPFPA效果相当, 但优于其他算法; 从表7可知, IBOA算法的求解效果与IBA、BPFPA相当, 但优于其他算法. 另外, 图3展示了IBOA算法和BOA算法在Survival数据集的最优解收敛曲线图, 从图3易知, IBOA算法的求解速度和精度较BOA算法高.IBOA求解Iris、Survival、CMC数据集的聚类效果图如图4–图6所示.
| 表 2 11种算法在Iris数据集上聚类结果比较 |
| 表 3 10种算法在Wine数据集上聚类结果比较 |
| 表 4 9种算法在Glass数据集上聚类结果比较 |
| 表 5 9种算法在Cancer数据集上聚类结果比较 |
| 表 6 10种算法在CMC数据集上聚类结果比较 |
| 表 7 8种算法在Survival数据集上聚类结果比较 |
|
图 3 IBOA与BOA求解Survival数据集函数收敛曲线图 |
4 结论
本文将精英策略的思想重新定义蝴蝶优化算法的局部搜索迭代公式且遗传算法相结合提出了一种改进的蝴蝶优化聚类算法, 通过求解1个人工数据集和5个UCI数据库中不同规模的数据, 统计分析结果表明IBOA算法能够避免陷入局部最优, 具有较快的收敛速度和较强的鲁棒性, 能够有效解决聚类问题且与其他聚类算法相比具有一定优势.
|
图 4 IBOA求解Iris数据集的聚类效果图 |
|
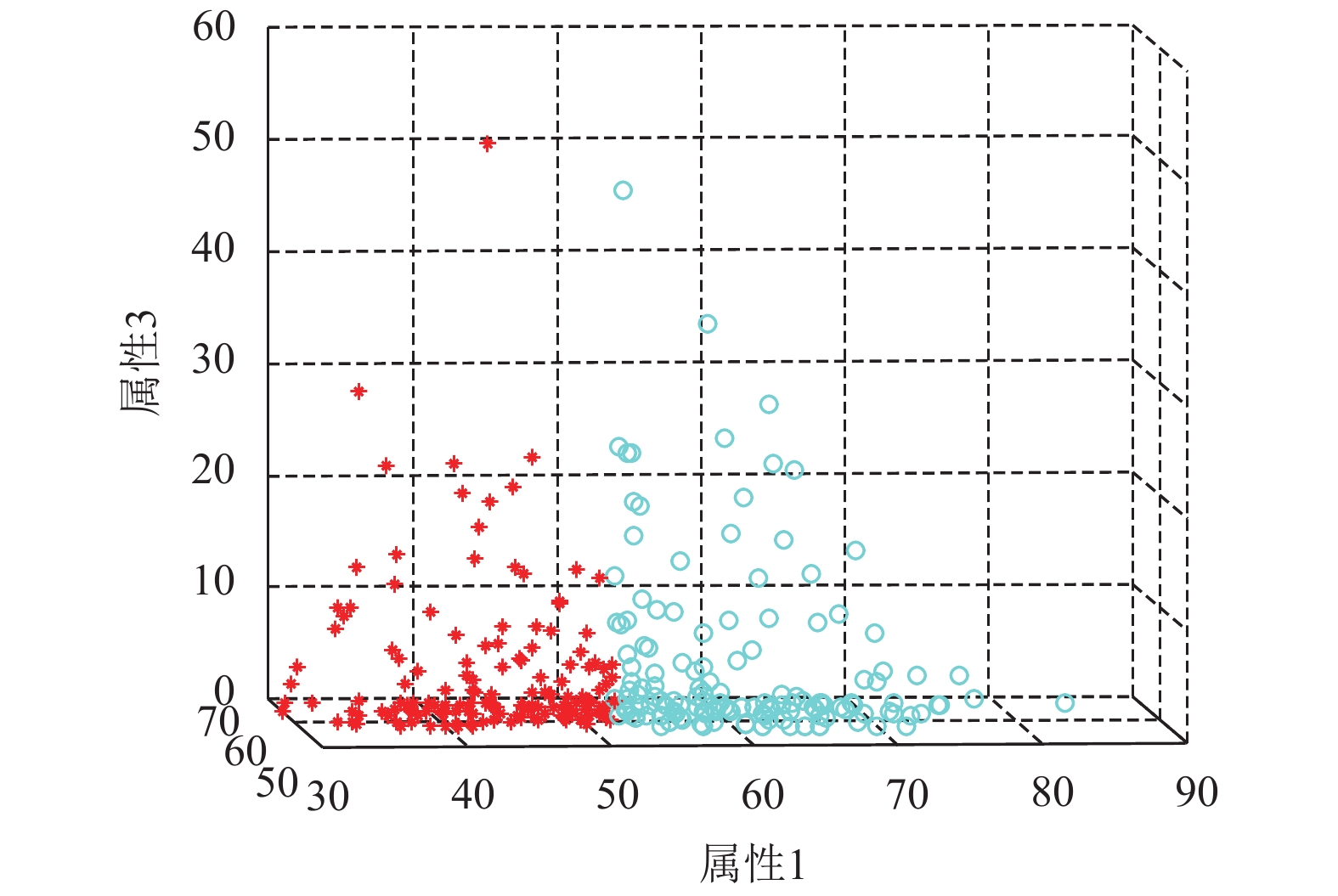
图 5 IBOA求解Survival数据集的聚类效果图 |
|
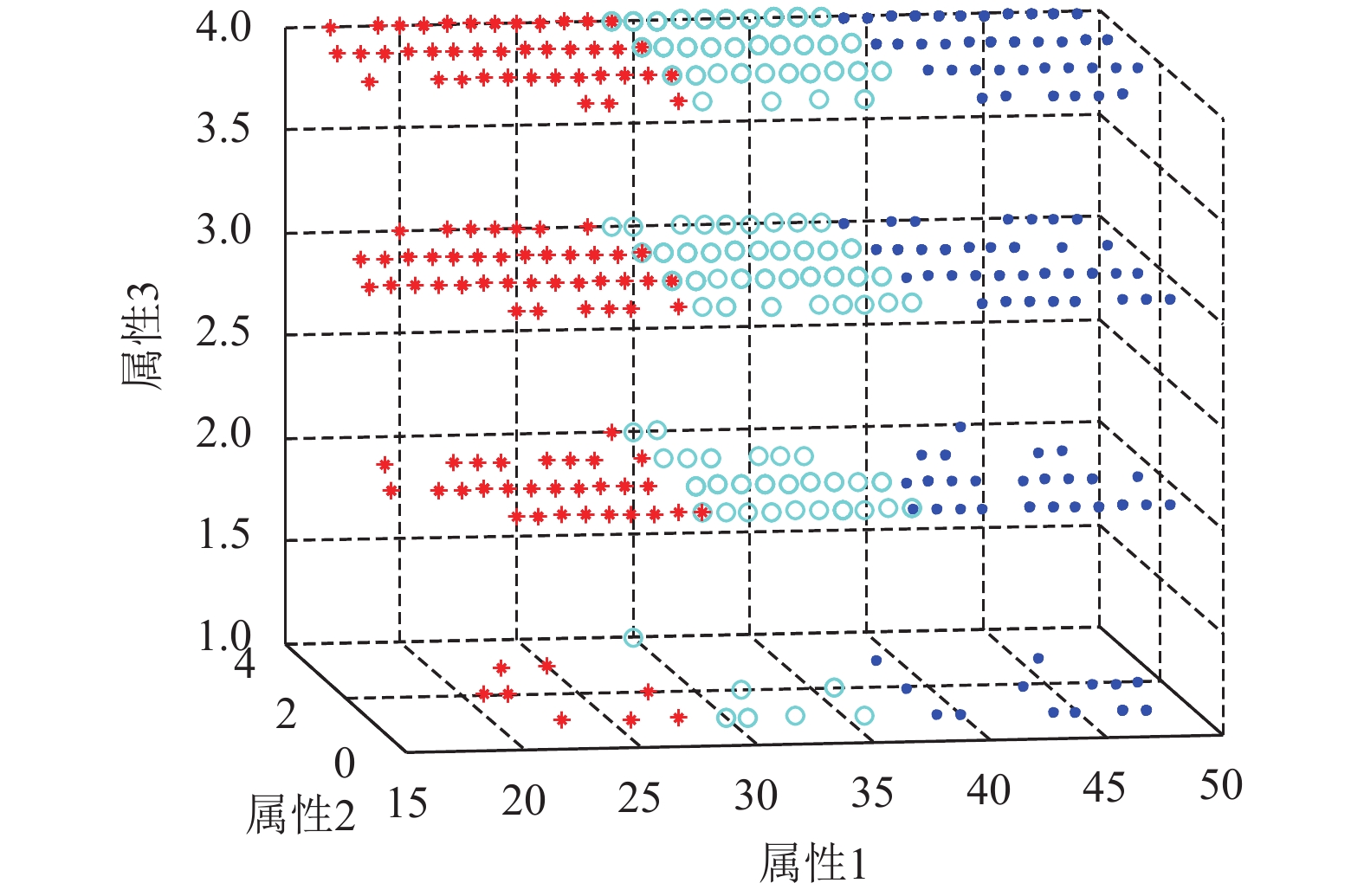
图 6 IBOA求解CMC数据集的聚类效果图 |
| [1] |
罗可, 李莲, 周博翔. 一种蜜蜂交配优化聚类算法. 电子学报, 2014, 42(12): 2435-2440. DOI:10.3969/j.issn.0372-2112.2014.12.015 |
| [2] |
杜明煜, 雷秀娟. 一种改进的求解聚类问题的萤火虫群优化算法. 陕西师范大学学报(自然科学版), 2014, 42(3): 20-23. |
| [3] |
王勇臻, 陈燕, 张金松. 一种改进的求解聚类问题的差分进化算法. 计算机应用研究, 2016, 33(9): 2630-2633. DOI:10.3969/j.issn.1001-3695.2016.09.014 |
| [4] |
杨辉华, 王克, 李灵巧, 等. 基于自适应布谷鸟搜索算法的K-means聚类算法及其应用. 计算机应用, 2016, 36(8): 2066-2070. DOI:10.11772/j.issn.1001-9081.2016.08.2066 |
| [5] |
沈小云, 衣俊艳. 面向聚类分析的自适应弹性网络算法研究. 计算机工程与应用, 2017, 53(9): 175-183. DOI:10.3778/j.issn.1002-8331.1611-0316 |
| [6] |
Wang R, Zhou YQ, Qiao SL, et al. Flower pollination algorithm with bee pollinator for cluster analysis. Information Processing Letters, 2016, 116(1): 1-14. DOI:10.1016/j.ipl.2015.08.007 |
| [7] |
熊珍, 傅秀芬. 求解聚类问题的异构蝙蝠算法. 计算机工程与设计, 2017, 38(3): 677-681, 728. |
| [8] |
张新明, 姜云, 刘尚旺, 等. 灰狼与郊狼混合优化算法及其聚类优化. 自动化学报. https://doi.org/10.16383/j.aas.c190617. [2020-03-26].
|
| [9] |
刘志鹏, 胡亚琦, 张卫卫. 自适应细菌觅食的FCM聚类优化算法研究. 现代电子技术, 2020, 43(6): 144-148. |
| [10] |
武森, 何慧霞, 范岩岩. 拓展差异度的高维数据聚类算法. 计算机工程与应用https://www.cnki.net/KCMS/detail/11.2127.tp.20200323.1607.004.html. [2020-03-24].
|
| [11] |
李珍萍, 田宇璇, 卜晓奇, 等. 无人仓系统订单分批问题及K-max聚类算法. 计算机集成制造系统. http://kns.cnki.net/kcms/detail/11.5946.TP.20200320.1423.010.html. [2020-03-20].
|
| [12] |
Arora S, Singh S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Computing, 2018, 23(3): 715-734. |
| [13] |
Wang GG, Deb S, Cui ZH. Monarch butterfly optimization. Neural Computing and Applications, 2019, 31(7): 1995-2014. DOI:10.1007/s00521-015-1923-y |
| [14] |
Arora S, Singh S. Butterfly algorithm with Lèvy Flights for global optimization. Proceedings of 2015 International Conference on Signal Processing, Computing and Control (ISPCC). Waknaghat, India. 2015. 220–224.
|
 2020, Vol. 29
2020, Vol. 29


