资源受限项目调度问题(Resource-Constrained Project Scheduling Problem, RCPSP)是一种典型的NP-hard问题^[1], 具有约束条件严苛、组合性强、求解范围广等特点, 其基本目标是在一定资源的约束下得到合理的调度方案, 使得时间或者项目成本得到最优化. 多技能资源受限项目调度问题(Multi-Skilled Resource-Constrained Project Scheduling Problem, MS-RCPSP/MSPSP)是在其基础上增加了技能约束的一种拓展性问题, 因其在软件开发、建筑工程、车间调度等方面的广泛应用而不断受到越来越多的学者的关注, 并衍生出许多求解方案. 比如, 任逸飞等人提出了一种包含双层决策及局部优化策略的混合算法对MSPSP进行求解, 并结合基于关键链的局部搜索算法提高了求解质量^[2]; Skowronski等人先后用基于调度优先级规则的元启发式算法^[3]、禁忌搜索算法^[4]和进化算法^[5]研究MSPSP, 并生成了一套专门针对MSPSP的基准数据集iMOPSE^[6], 为后世研究该问题提供了重要参考依据.

总的来说, 目前所使用的各种算法都仅能针对部分数据对象而不断靠近最优解, 如何提出合适的算法为MSPSP求出更优解是目前研究努力的一个方向. 本文在对比了各种算法之后, 考虑到发展已久的遗传算法(Genetic Algorithm, GA)^[7]在寻优搜索能力、鲁棒性和兼容性等方面的良好表现, 选择其作为本文的基本算法. 考虑到该算法存在早熟收敛和后期收敛速度慢的问题, 学者们在其基础上进行了相关改进, 并用于求解MSPSP问题. 比如, Laszczyk等人在经典的非支配遗传算法的基础上提出了一种新的选择算子, 提高了搜索效率^[8]; Lin等人提出了一种遗传规划的超启发式算法, 将遗传算法作为一种宏观策略, 统筹调度十种启发式规则进行求解^[9]. 本文针对MSPSP的特点, 在细化遗传算法的求解过程的基础上, 对其选择、交叉和排序过程分别进行了改进.

1 MSPSP介绍 1.1 问题描述

MSPSP的基本概念是: 一个项目中涉及多个任务, 任务之间存在时间约束关系, 项目中的各种资源都具备一种或多种技能, 问题的目标是在满足各种约束的条件下合理调度和分配已有的资源和任务, 使得完成整个项目的总时间或总成本最小化.

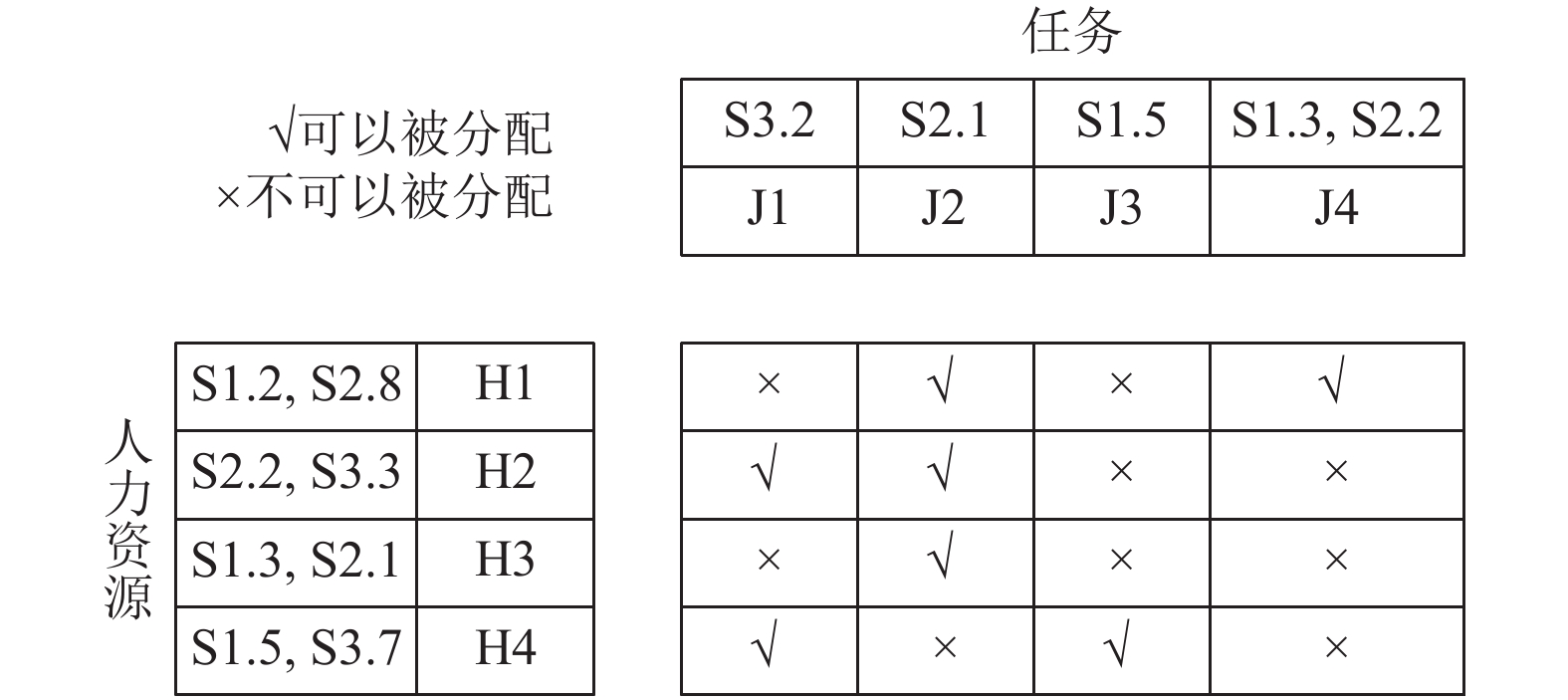
一般而言, 问题中的资源都指人力资源, 以图1为例, J1~J4表示任务, H1~H4表示资源, 以J1为例, 它需要具备技能S3且技能等级达到3.2的人员, 在H1~H4中只有H2和H4是满足的, 因此对于J1来说H2和H4可以被分配给它. 当确定人力资源的可分配权后, 再结合相关时间约束和资源约束, 才能进一步确定最终的分配情况.

1.2 数学模型

为了便于描述MSPSP的数学模型, 首先引入如下符号定义:

J: 任务集合, J={1, 2, ···, m};

H: 资源集合, H={1, 2, ···, n};

S: 技能集合;

d_j: 完成任务j的工期;

b_j: 任务j的开始时间;

f_j: 任务j的结束时间;

k_jh: 任务j所需要的资源 h的数量;

P_j: 任务j的前置任务集合;

K_h: 资源h的数量;

w_h: 资源h的单位成本;

S_h: 资源h所拥有的技能集合;

J_h: 资源h可完成的任务集合;

l_s: 技能s的等级;

q_s: 技能s的类别;

α: 优化目标的权重系数;

T: 工作持续时间;

Q_jht: 0-1变量, 资源h在t时刻作用于任务j时为1, 否则为0.

MSPSP的数学模型为:

目标函数:

$\min {F_s} = \min \alpha {F_\tau } + (1 - \alpha ){F_c}\quad \alpha \in [0,1]$

(1)

其中,

${F_\tau } = \mathop {\max }\limits_{j \in J} {f_j}$

(2)

${F_c} = \sum\limits_{j = 1}^m {\sum\limits_{h = 1}^n {{d_j}{w_h}\theta (jh)} } $

(3)

约束条件:

${f_j} = {b_j} + {d_j}\quad \forall j \in J$

(4)

${f_p} \le {f_j}\quad \forall j \in J,\forall p \in {P_j}$

(5)

${S_h}\not = \emptyset \quad \forall h \in H,{S_h} \in S$

(6)

${w_h} \ge 0\quad \forall h \in H$

(7)

$\sum\limits_{j = 1}^m {{Q_{jht}} \le 1\quad \forall h \in H,\forall t \in T} ,\forall j \in J$

(8)

${l_s} \ge {l_{{s_i}}} \wedge {q_s} = {q_{{s_i}}}\quad \forall i \in {J_h},\exists s \in {S_h}$

(9)

$\theta (jh) = {Q_{jht}} = \left\{ {\begin{array}{*{20}{c}} {1\quad {b_j} \le t \le {f_j}}\\ {0\quad t \notin [{b_j},{f_j}]} \end{array}} \right.\quad \forall j \in J,\forall h \in H,\forall t \in T$

(10)

式(1)中的 ${F_\tau }$ 和 ${F_c}$ 分别表示工作的总时间和总成本, 两者是相互制约的关系, 通过权重系数 $\alpha $ 关联起来, 构成总的优化目标 ${F_s}$ . $\alpha $ 的取值将决定优化对象是单目标还是多目标, $\alpha {\rm{ = }}0$ 时是成本优化, $\alpha {\rm{ = }}1$ 时是时间优化, $\alpha \in (0,1)$ 是综合考虑时间和成本的多目标优化. 本文主要考虑单目标优化. 式(4)和式(5)表示任务的时间约束. 式(6)~式(8)是对人力资源的约束: 式(6)要求每种人力资源至少具备一种技能; 式(7)体现了人员成本的合理性; 式(8)表示单个资源在同一时间内只能使用一种技能去执行一项任务. 式(9)是技能约束, 规定了在为各个任务节点分配资源时, 必须满足该任务对资源的技能种类和技能等级的需求. 式(10)的定义是为了方便计算成本消耗.

2 改进遗传算法 2.1 编解码方案

根据问题选择合适的染色体编码方式是遗传算法的第一步, 鉴于MSPSP是要寻找满足约束条件的任务和资源的最佳排列, 本文选择基于优先级数组的整数编码, 以更直观地展示和表达调度结果. 在遗传算法中, 每条染色体对应一个任务链, 以优先级数组进行表示时, 数组中的元素(即染色体的基因)是任务的权重, 数组的下标表示任务编号, 数组的长度等于任务总数.

编码之后还需要进行解码才能形成完整的调度方案. 本文选择串行调度机制^[10]实行解码操作, 主要分为两个部分:

(1) 在不考虑技能约束的情况下, 根据任务的权重生成任务序列, 当权重相等时, 任务编号小的优先;

(2) 根据技能约束和资源约束对资源进行分配, 在此过程中如果发现资源分配冲突则需要对任务序列进行调整, 如果无法通过调整满足需求则放弃该方案.

2.2 适应度函数

遗传算法一般会选择问题的目标函数作为适应度函数, 但MSPSP的目标函数是最小化目标, 不满足适应度函数的最大化需求, 因此需要做一定转化, 最终的适应度函数如式(11)所示.

${f_g}({c_k}) = \frac{{{F_{s\_\max }} - {F_s}}}{{{F_{s\_\max }} - {F_{s\_\min }}}}$

(11)

其中, ${f_g}({c_k})$ 是个体 ${c_k}$ 的适应度函数, ${F_s}$ 是当前个体的目标值(即目标函数值), ${F_{s\_\max }}$ 和 ${F_{s\_\min }}$ 分别是当前群体中的最大目标值和最小目标值.

2.3 基于群体共享的小生境选择

得到种群的适应度后, 需要根据适应度大小对种群中的个体进行初步筛选, 挑选出适应度较好的一批个体, 为后续的交叉和变异做准备. 传统的直接通过比较个体适应度大小来决定生存权的方式会带来一些问题:

(1) 算法搜索初期, 适应度很好的一批个体不但拥有更长的生存时间, 而且易被视为优良父代将本身的基因传承下去, 进而影响整个种群的进化方向, 从而削弱了算法的全局搜索能力;

(2) 算法搜索后期, 经过多代的进化, 个体间的差异变小, 种群多样性降低, 演变成了近亲繁殖, 在此基础上生成的后代也很难有新的变化, 最终算法可能会陷入局部最优.

为了防止种群的多样性被破坏, 本文在遗传算法的选择阶段融入基于群体共享的小生境技术^[11]. 其基本过程是: 首先将原始种群分为若干子种群, 接着从中挑选出一个优质种群作为共享种群, 然后在共享种群和普通种群内部独立进行交叉、变异操作, 生成新一代种群, 并不断重复这种操作, 直到满足终止条件为止. 将小生境技术与遗传算法相融合, 能够增强算法的全局搜索的能力, 加快算法的收敛速度.

2.3.1 定义说明

为了实现上述算法, 首先给出如下定义:

定义1. 个体间距离

在基于群体共享机制的小生境方法中, 可以利用海明距离来辅助判断个体之间的相似程度, 相似度不高的个体才能进行交配, 以保证种群的多样性. 为了方便计算海明距离, 需要先将个体由实数编码转为二进制编码, 然后再根据式(12)求得个体 ${c_i}$ 和 ${c_j}$ 之间的海明距离, 其中, $binLen$ 表示染色体二进制编码的长度, G表示整个种群.

$\begin{array}{l} d({c_i},{c_j}) = ||{c_i} - {c_j}|| = \sqrt {\displaystyle \sum\limits_{k = 1}^{binLen} {{{({c_{ik}} - {c_{jk}})}^2}} } \\ \forall {c_i},{c_j} \in G,{c_i} \ne {c_j} \end{array}$

(12)

定义2. 个体共享度

个体共享度是借助个体间海明距离来度量其相似程度的一种表达, 如式(13)所示, 个体之间相似度越大, 个体共享度就越大.

$s({c_i},{c_j}) = 1 - \frac{{d({c_i},{c_j})}}{{binLen}}$

(13)

定义3. 群体共享度

群体共享度是对个体在群体中的特异性的度量, 是个体与群体中的其他个体间的个体共享度之和, 如式(14)所示.

${s_g} = \sum {s({c_i},{c_j})} \quad \forall {c_i},{c_j} \in G,{c_i} \ne {c_j}$

(14)

2.3.2 确定式采样选择

在各个子群体的进化过程中, 为了保证优质基因能够遗传下去, 与文献[11]不同的是, 本文采用确定式采样选择法^[12]进行个体选择, 避开传统轮盘赌方式带来的统计误差. 具体操作过程是:

Step 1. 计算各个子种群中的个体在下一代中的期望数目:

${N_{exp}}({c_i}) = subS\!i{\textit{z}} e \cdot \frac{{f({c_i})}}{{\displaystyle \sum\limits_{i = 1}^{subSi{\textit{z}} e} {f({c_i})} }}\;\;\;{\kern 1pt} i = 1,2, \cdots ,subS\!i{\textit{z}} e$

(15)

Step 2. 取 $\left[ {{N_{\rm {exp}}}({c_i})} \right]$ 作为 ${c_i}$ 在下一代中的生存数目, 其中 $\left[ {{N_{\rm {exp}}}({c_i})} \right]$ 表示不大于 ${N_{\rm {exp}}}({c_i})$ 的最大整数;

Step 3. 根据 ${N_{\rm {exp}}}({c_i})$ 的小数部分对所有个体进行排序, 选择最大的 $subS\!i{\textit{z}}e - \displaystyle \sum\limits_{i = 1}^{subS\!i{\textit{z}}e} {\left[ {{N_{\rm {exp}}}({c_i})} \right]}$ 个个体进入到下一代种群中.

这种方式能够确保每个子群体中适应度较大的个体都能存活到下一代.

2.3.3 子种群适应度和规模调整

为了减少算法中相似个体的不断聚合, 需要根据子群体的群体共享度不断调整其适应度和种群规模.

调整的基本规则是:

(1) 根据共享种群的群体共享度占总群体共享度的比值, 略微调高共享种群的适应度;

(2) 当普通种群的群体共享度大于共享种群的群体共享度时, 调低普通种群的适应度, 反之调高;

(3) 在总的种群规模不变的情况下, 根据种群的适应度比例重新分配子种群的规模.

对于共享种群的适应度调整:

${f_{\rm {share}}} = {f_{\rm {share}}} \cdot \exp ({N_e}\frac{{{s_{\rm {share}}}}}{{\displaystyle \sum\limits_{j = 1}^{{N_{\rm {sub}}}} {{s_g}(j)} }})$

(16)

对于普通种群的适应度调整:

${f_{\rm {others}}} = {f_{\rm{others}}}\exp \left( - \frac{{{s_g} - {s_{\rm {share}}}}}{{{s_{\rm {share}}}}}\right)$

(17)

对于各个子种群规模的调整:

$subS\!i{\textit{z}} e(i) = \frac{{{f_g}(i)}}{{\displaystyle \sum\limits_{j = 1}^{{N_{\rm {sub}}}} {{f_g}(j)} }} \cdot popS\!i{\textit{z}} e\quad i = 1,2, \cdots ,{N_{\rm {sub}}}$

(18)

其中, ${s_{\rm {share}}}$ 表示共享种群的群体共享度, $subSi{\textit{z}}e(i)$ 表示第i个子种群的规模, ${f_g}(i)$ 表示第i个子种群的适应度值.

2.4 基于修复机制的单点交叉

遗传算法中的交叉操作能够生成继承了父代基因的新个体, 提高算法的全局搜索能力, 其中最常见的是单点交叉法. 传统的单点交叉的过程是: 在父辈个体中随机选择一个交叉点, 将该交叉点之后的基因互换, 从而生成了两个新的子个体. 本文的染色体是任务时序链, 使用基本的单点交叉后容易打破时序约束, 且新生成的子个体中可能出现重复项和缺失项. 为了保证子代个体的有效性, 本文结合随机生成的交叉概率 ${P_c}$ , 在基本的单点操作基础上增加了相关修复策略, 如图2所示.

具体的修复过程是: 经过基本的单点交叉后, 首先找到子代个体中重复的编号, 子代c₁中是1和3, c₂中是4和6; 然后将c₁交叉点前的重复编号与c₂交叉点后的重复编号依次进行交换, 即c₁中交叉点前的1和3分别与c₂交叉点后的4和6交换, 同理, 也将c₂交叉点前的重复编号与c₁交叉点后的重复编号依次进行交换, 即c₂中交叉点前的4和6分别与c₁交叉点后的3和1交换; 最后交换后的结果即为修复的子代个体, 该子代个体都满足任务的时序约束, 且没有重复项.

但是, 交叉完后的子代个体的适应度并不一定比父代强, 为了在交叉后尽量保留适应度相对较好的个体, 在此引入父子竞争机制来进一步筛选出能够进入下一代繁殖的个体: 对父代c₁、c₂和子代c₁、c₂四个个体的适应度进行排序, 选择适应度最好的两个作为最终的新生代个体进入下一次繁殖和进化.

2.5 基于多重验证的变异

除了交叉外, 遗传算法中的变异操作也能生成新的个体, 辅助交叉操作维护种群的多样性, 增强算法的局部搜索能力. 与交叉不同的是, 变异是根据变异率 ${P_m}$ 在单个染色体上对其部分基因进行突变, 从而产生新的个体.

对于MSPSP问题而言, 为了使变异后的个体仍旧满足约束条件, 在执行传统的变异操作后, 还需对新个体进行时序约束验证, 只有验证通过的个体才能保留下来, 否则变异失效. 另外, 如果变异后的个体适应度太低, 则表明该方案不太可取, 且会影响整个子群体的适应度, 因此还需对新个体进行适应度检验.

本文设计的基于多重验证的变异过程如下:

Step 1. 随机为子种群中的所有个体分配概率 $p({c_i})$ ;

Step 2. 选择一个个体, 判断是否满足 $p({c_i}) \le {P_m}$ , 如果是则执行变异操作, 否则另选个体进行判断;

Step 3. 在所选个体上随机选择两个任务 $c_i^{{k_1}}$ 和 $c_i^{{k_2}}$ 进行交换;

Step 4. 判断新个体是否满足时序约束, 且适应度比旧个体高, 如果都满足则用新个体代替旧个体; 否则抛弃新个体, 保留旧个体;

Step 5. 判断当前种群中的所有个体是否都检测完毕, 如果是, 则结束变异操作; 否则转到Step 2.

2.6 算法总流程

改进遗传算法的详细步骤为:

Step 1. 设置遗传算法的相关参数(种群规模 $popSi{\textit{z}}e$ , 变异概率 ${P_m}$ , 最大迭代次数 ${N_{\rm {iter}}}$ ), 并用贪心算法初始化种群;

Step 2. 划分子种群;

Step 3. 计算个体的适应度, 并在各个子种群内独立执行进化操作: 首先按照确定式采样规则进行个体选择, 然后执行基于修复机制的单点交叉操作, 最后完成基于多重验证的变异操作;

Step 4. 判断子群体进化次数 ${k_{\rm {sub}}}$ 是否达到上限值 ${N_e}$ , 如果是则先将 ${k_{\rm {sub}}}$ 清零, 再转到Step 5; 否则转到Step 3;

Step 5. 计算子种群的平均适应度, 选择适应度值最高的作为共享种群;

Step 6. 根据群体共享度和适应度调整所有子种群的适应度和规模;

Step 7. 淘汰连续几代表现最差的子群体, 并产生相同规模的新群体进行替换;

Step 8. 判断当前迭代次数是否达到上限, 或者连续几代的求解结果偏差是否满足收敛条件, 如果满足任意一条则结束算法, 输出结果; 否则转到Step 3.

算法的流程图如图3所示.

3 实验分析

用Python实现了针对MSPSP的改进遗传算法后, 为了验证算法的性能, 本文在iMOPSE^[6]数据集上进行了实验, 并与其他算法的求解结果进行了对比. 实验中, 算法的参数设置如表1所示.

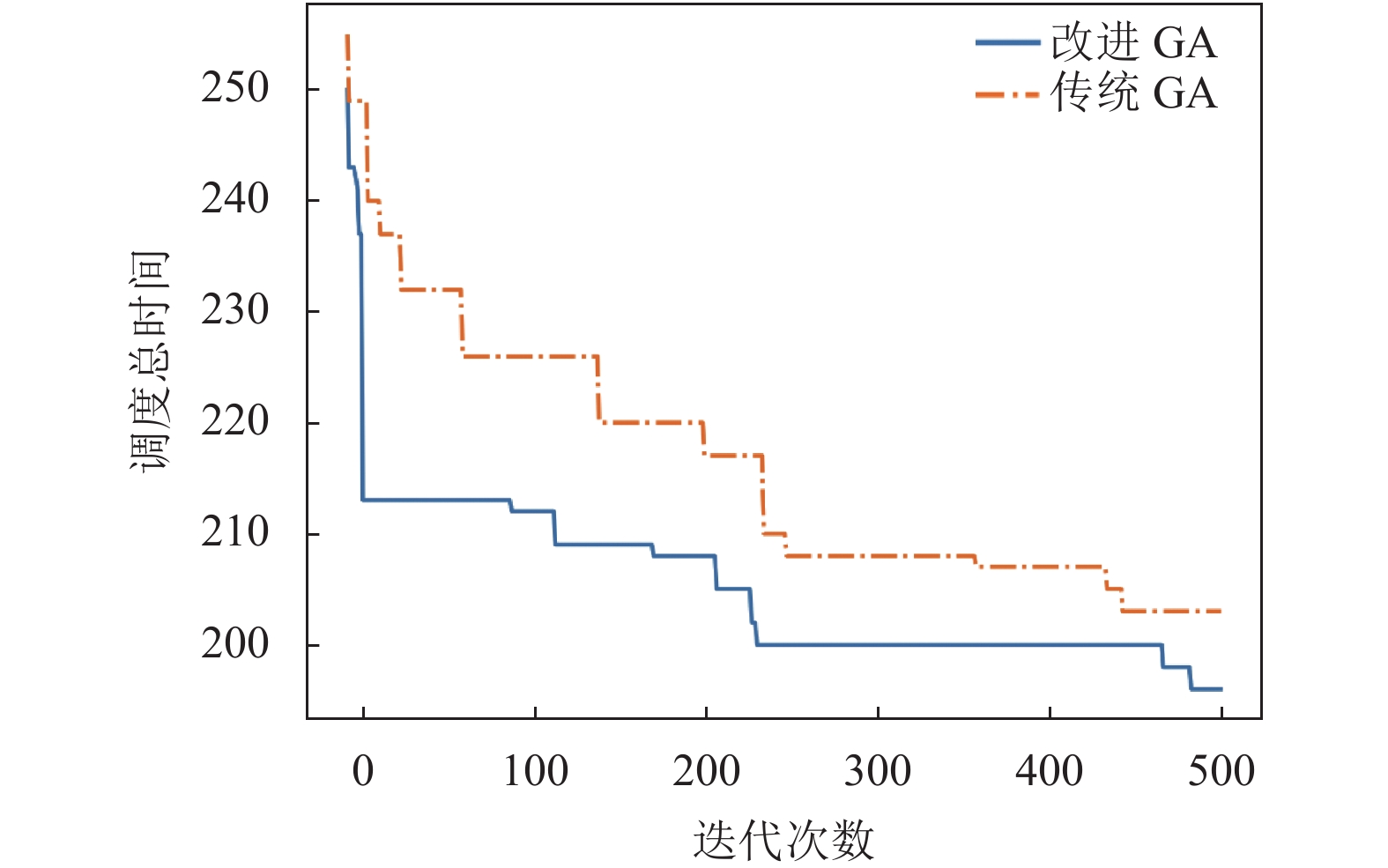
在取相同参数的情况下, 改进遗传算法和传统遗传算法在10_20_46_15算例上的求解效果如图4所示, 可以看出, 改进算法的收敛速度更快, 求解结果更优.

使用改进遗传算法对整个iMOPSE数据集进行求解, 分别取 $\alpha {\rm{ = }}1$ (时间最优)和 $\alpha {\rm{ = 0}}$ (成本最优), 每个实例运行20次, 将结果与文献[13]中的混合蚁群算法的结果进行对比, 如表2所示. 可以看出, 不管是以时间最优还是成本最优为目标, 改进遗传算法都能求得更优的解, 且从多次求解的标准差来看, 大部分情况下改进遗传算法都更加稳定.

4 结束语

本文针对MSPSP问题的特点, 在传统遗传算法的基础上, 融入了基于群体共享的小生境技术, 提高了种群信息的利用率, 并针对MSPSP的时序约束, 分别为交叉和变异操作增加了修复和验证机制, 进一步确保了个体的合法性. 经实验验证分析可知, 改进后的遗传算法相较于传统遗传算法和混合蚁群算法的收敛速度更快, 求解结果更优, 稳定性更强, 且能在iMOPSE数据集上取得良好效果, 为研究相关实际问题提供了一定参考价值.