地下浅层震源定位是地下浅层空间研究的热点问题, 该方法在侵彻弹地下浅层空间爆炸, 以及近地表人工爆破等军事方面以及能源勘探开发, 工程和灾害地质, 金属矿勘探等民用方面具有重要的应用价值, 它是重建爆破场区能量场以及试验验证的有效手段, 因此, 震源定位具有重要的工程应用价值. 目前, 地下震源定位中广泛运用DOA (Direction Of Arrival)—波达方向估计进行定位.

基于DOA模型定位是通过多组传感器节点获取的多个角度信息来计算震源估计位置.

DOA模型求解方法主要分为两类: 传统的解算方法和智能优化求解方法. 传统算法为(1)最小二乘+Taylor算法, 该算法首先用最小二乘法解出震源初始估计值, 再利用泰勒中值定理对定位方程展开, 然后只保留一次导数, 在初始位置的基础上, 在每一步迭代时, 都沿当前点函数值下降的方向进行, 但该算法对初始解的依赖性比较大, 定位精度会随初始值的多次迭代后误差累加, 从而使定位精度降低^[1]; (2)基于几何约束加权被动定位算法, 该算法将震源位置与传感器节点的距离作为参数, 两两传感器在空间中进行交叉定位, 再计算空间中各个交叉点的权值, 该方法对定位参数精度的要求比较高, 否则会出现交叉点异面的情况, 在计算震源交叉点权值时, 受权值的归一化影响, 可能导致最终解偏离真实震源解, 使误差增大. 智能优化求解方法主要为PSO (Particle Swarm Optimization)粒子群定位算法, 因为在该算法中, 粒子运动状态受速度—位移影响, 限制了粒子的搜索范围, 使得粒子只能在特定的轨迹进行搜索, 不能脱离粒子群本身, 容易陷入局部最优, 缩小了搜索范围并使最终定位结果不准确.

针对以上定位算法的不足, 本文开展了一种基于QPSO (Quantum Particle Swarm Optimization)量子粒子群的地下浅层震源定位方法研究. 将QPSO算法应用到求解DOA震源定位方程中, 该方法避免了传统定位算法(最小二乘+Taylor等)对初值过分依赖问题、几何约束加权法产生的异面问题以及粒子群算法搜索轨迹受限的问题, 同时扩大了搜索范围, 并且使震源粒子在空间范围搜索能力覆盖到整个空间, 增强了搜索能力, 对实现地下浅层震源的高精度定位具有重要意义.

1 基于DOA的震源定位模型构建

定位模型的构建对定位结果的影响至关重要, DOA—波达方向, 指空间中信号的到达方向, 即传播信号到达各传感器阵列阵元的角度参数信息.

首先利用传感器节点的坐标信息以及震源与传感器间的角度信息, 构建DOA震源定位模型.

在实际震源定位中, DOA震源定位模型的建立是在预设的试验区域范围内的不同位置布设多个无线传感器节点, 传感器的布站与信号的到达角度紧密相连, 通过震源信号到达各个传感器的角度信息(即俯仰角和方位角), 建立定位方程从而能够对单目标震源进行定位, 进一步计算出目标震源的具体位置.

具体模型如图1所示^[2].

根据DOA三维震源定位模型, 利用传感器坐标及与目标震源获取的角度信息间联系, 建立三维空间震源定位方程组:

$ \left\{ {\begin{aligned} &{{\tan}{\theta _i} = \frac{{x - {x_i}}}{{y - {y_i}}}}\\ &{\tan {\varphi _i} = \frac{{z - {z_i}}}{{{r_i}}}}\\ &{{r_i} = \sqrt {{{(x - {x_i})}^2} + {{(y - {y_i})}^2}} } \end{aligned}} \right. $

(1)

整理可得:

$ \left\{\begin{aligned} & x_i-y_i\tan \theta_i=x-y\tan \theta_i\\ & z=\sqrt {(x-x_i)^2+(y-y_i)^2} \tan \varphi_i+z_i \end{aligned}\right.$

(2)

其中, i=1, 2, …, n; $(x,y,z)$ 为所求震源坐标, $({x_i},{y_i},{z_i})$ 为已知传感器 $i$ 坐标, ${\theta _i}$ 和 ${\varphi _i}$ 分别是传感器 $i$ 与震源间测得的方位角与俯仰角.

以上式(2)是构建的DOA震源定位方程组, 本文针对特定区域范围内震源定位问题, 引入量子粒子群方法对DOA定位方程进行解算, 对目标震源进行估计.

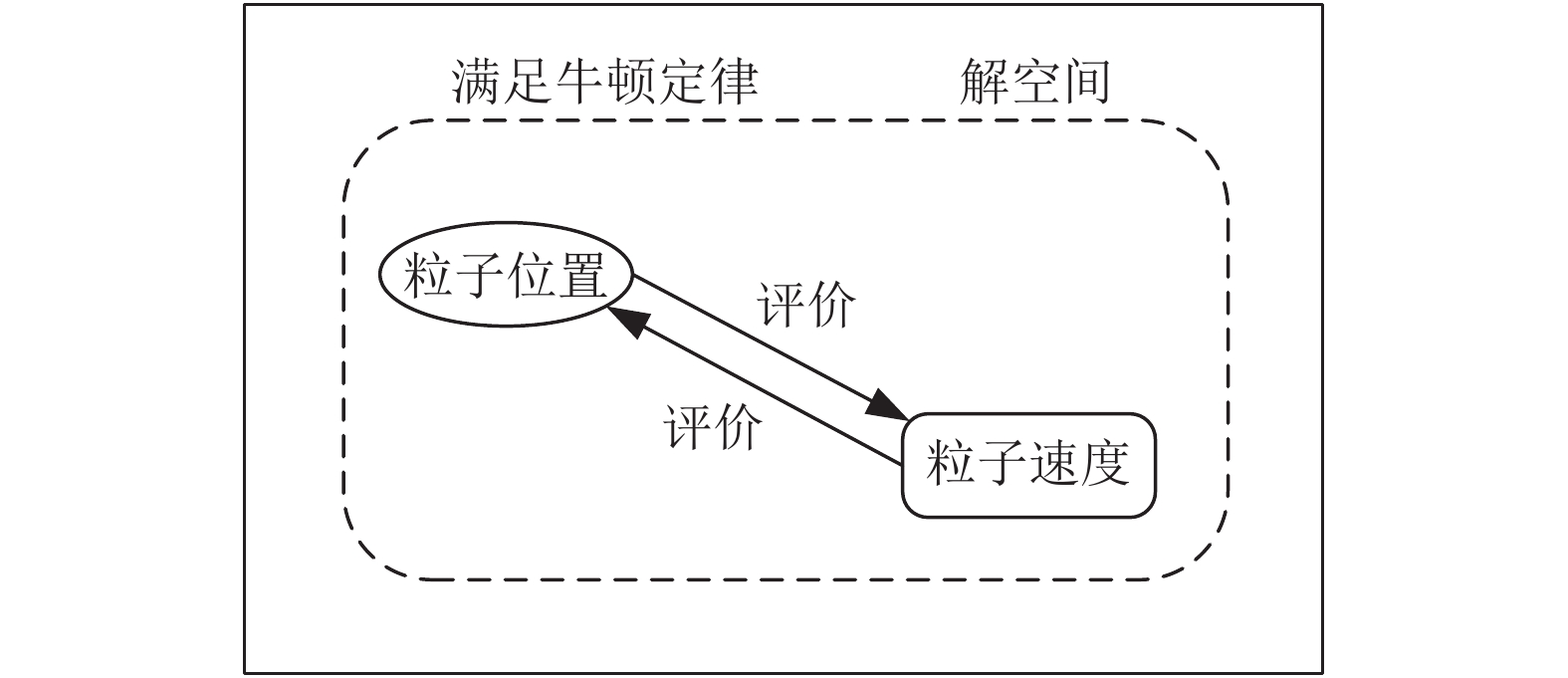
2 基于量子粒子群算法的DOA震源定位模型的解算 2.1 量子粒子群(QPSO)算法原理

在PSO粒子群中, 粒子的运动状态具有一定的约束性, 即在PSO系统中, 粒子运动状态受速度—位移条件制约, 粒子只能在粒子群附近进行运动, 即使此时位置优于当前全局最好位置Gbest, 其局限性如图2所示,

针对PSO粒子搜索的局限性, 为了避免粒子局限于只能在粒子群附近搜索的弊端, 需要扩大搜索范围, 将量子系统引入到PSO中.

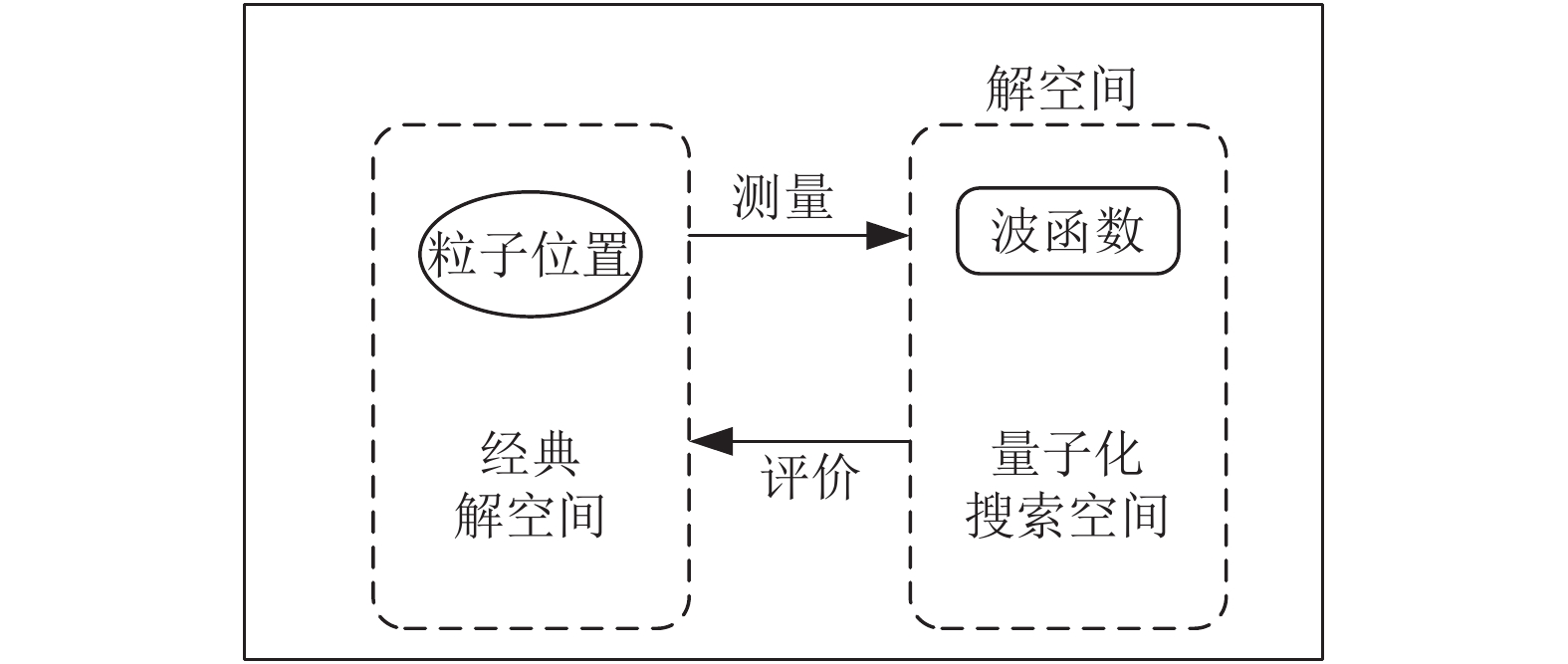
QPSO量子化系统的特点在于, 引入了波函数, 使得粒子的运动状态由波函数决定, 具有随机性和不确定性. 测量前, 粒子没有既定的轨道束缚, 会以一定的概率出现在任何位置, 能以一定的概率在空间范围内任意搜索, 随机程度高, 能够达到全局搜索的目的, 摆脱了粒子运动的局限性^[3]. 另外, 速度信息和位置信息归于一个参数, 算法收敛精度高. QPSO粒子运动状态如图3所示.

为了确保算法的收敛性, 每个粒子必须收敛到它自己的局部吸引子P, $P = ({P_{i,1}},{P_{i,2}},\cdots,{P_{i,n}})$ , ${P_{i,n}}$ 是第i个粒子在第n维的局部吸引子:

${P_{i,n}} = {{\left( {{\varphi _1} * {P_{ibest,n}} + {\varphi _2} * {G_{best}}} \right)} / {({\varphi _1} + {\varphi _2})}}$

(3)

其中, ${\varphi _1}$ 和 ${\varphi _2}$ 是介于0和1之间的随机函数. 引入一个平均最优位置 $mbest$ 来计算粒子的下一步迭代的变量 $L$ , 定义为所有粒子的全局极值的平均值^[4], 公式如下:

$mbest = \frac{1}{M}\sum\limits_{i = 1}^M {{P_i} = \left(\frac{1}{M}\sum\limits_{i = 1}^M {{P_{i,1,\cdots,}}\frac{1}{M}} \sum\limits_{i = 1}^M {{P_{i,n}}} \right)} $

(4)

其中, $M$ 是粒子群的个数, ${P_i}$ 是粒子 $i$ 的全局极值. 因此可得到参数 $L$ 的计算公式:

$L(t + 1) = 2*\beta *\left| {mbest - x(t)} \right|$

(5)

进而可得到粒子的进化过程为:

$ \begin{aligned}[b] & x(t + 1) = p \pm \beta *\left| {mbest - x(t)} \right|*\ln ({1 / u})\\ & u ={\rm rand}(0,1) \end{aligned} $

(6)

其中, CE系数 $\;\beta $ 具有系数创造力, 我们采用动态线性递减策略, 由理论分析可知, 该种方法会随种群迭代的增加而逐步减小势阱长度, 过程类似于退火^[5,6], 公式如式(7):

$\beta (t) = ({\beta _0} - {\beta _1}) * ({{({t_{\max }} - t)}/ {{t_{\max }}}}) + {\beta _1}$

(7)

2.2 基于QPSO的DOA算法的具体实现过程 2.2.1 目标函数的构建

目标函数的选择决定了种群局部最优和全局最优位置的选取, 从而进一步影响算法最终的准确性, 针对这一问题, 在基于DOA定位的基础上, 利用已知节点的信息, 如何构建合理的目标函数, 成为本节研究的重点.

极化度是衡量传感器节点信息准确度的一项指标, 因此利用基于协方差矩阵(ACM)(Adaptive Covariance Matrix)的极化分析算法, 计算各个节点的直达P波时段的极化度, 利用极化度信息来评估各节点的数据质量: 极化度越高, 说明传感器与土壤耦合程度越高, 线性偏振特性越好, P波角度信息越有效.

因此, 通过ACM极化分析方法找到极化度最高的两个传感器节点的坐标信息, 角度信息, 结合DOA模型的定位方程, 构建目标函数, 表达式如式(8)所示,

$f(x,y,z) = \sum\limits_{i = 1}^2 {(({x_i} - x + (y - {y_i})} \cdot\tan {\theta _i}{)^2} + {(z - {z_i} - {r_i}\tan {\varphi _i})^2})$

(8)

其中, ${r_i} = \sqrt {{{(x - {x_i})}^2} + {{(y - {y_i})}^2} + {{(z - {z_i})}^2}} $ , $\left( {x,y,z} \right)$ 为目标位置; $\left( {{x_i},{y_i},{z_i}} \right)$ 为传感器节点位置坐标, $i = 1,2$ , 为极化度最高的两个节点.

式(8)代表极化度最高的两个传感器的角度和坐标信息与估计震源的差值, 目标函数值越小, 证明在解空间内寻找的估计震源位置与目标震源越接近, 我们采用量子粒子群方法对该目标函数进行寻优.

2.2.2 QPSO的粒子更新方式

在QPSO中, 将速度和位置信息归于一个参数, 同时引入一个 $\delta $ 势阱中心P作为每个粒子的领导者, 它主导着粒子的运动方向; 同时引入势阱长度参数L, L具有其自身的创造性, 它表示震源粒子搜寻的范围. L值越大, 粒子找到最优位置的可能性就会增加, 创造能力就越强. 在下一步位置寻找前, 需要对势阱长度参数L不断进行评价. 因此, 在量子化空间内, 每个粒子就是以P点为中心, L为半径进行大规模搜索.

在评估完粒子个体创造力后, 从式(6)获得新位置, 并完成搜索空间到解空间的状态转换.

2.2.3 基于QPSO的DOA定位算法具体实现过程

具体流程如图4所示.

步骤1. 首先设定搜索范围, 在搜索区域x (–100 m, 100 m), y (–100 m, 100 m), z (–50 m, 0 m)内随机生成42个3维的震源位置(x, y, z), 并将此时的震源位置看作是当前每个震源的最好位置, 即个体最好位置pbest(personal best position);

步骤2. 根据2.2.1节所选的目标函数式(8)计算震源群中所有粒子的适应度值, 选适应度值最小的粒子, 设为当代震源群中的最优震源位置Gbest (Global best position)即全局最好位置^[7];

步骤3. 为了增大各粒子间的信息交流, 引入震源种群的平均最优位置(mbest), 即把这42个震源粒子的三维坐标各自取平均即可得到, 利用式(4)计算42个震源平均最优位置mbest^[8];

步骤4. 通过式(6)来更新每个震源的位置;

步骤5. 评价更新后震源粒子的优劣, 从而更新pbest和Gbest; 如果当前震源粒子新位置的适应度值小于上一个个体最优pbest的适应度值, 则更新pbest和其所对应的适应度值, 否则将保留原来的pbest, 若当前震源粒子的适应度值小于所有的震源粒子所经历的Gbest时, 则将更新Gbest作为新的全局最优位置;

步骤6. 当迭代次数达到 ${t_{\max }}$ 时, 说明此时已找到一个最优震源位置Gbest, 并将其输出. 通过以上方法可在所有粒子群中找到最优化的震源位置.

3 算法仿真

为验证该算法的可行性, 本文建立地下震源定位仿真模型如图5, 在预设区域x (–100 m, 100 m), y (–100 m, 100 m),z (–50 m, 0 m)范围内, 分布7个传感器节点对算法进行仿真测试, 假设炸点坐标已知为(–10 m, 15 m, –40 m), 7组传感器信号节点的角度参数信息采用信噪比为–10 dB的高斯白噪声, 炸点位置及传感器信息如表1所示.

本文采用传统PSO算法, 改进PSO算法即种群多样性反馈分组粒子群DGPSO算法, 以及量子粒子群QPSO算法分别对该定位模型进行模拟仿真, 参数设定如下.

粒子群算法的参数设置: 维数为3, 种群规模42, 迭代次数2500, 学习因子 ${c_1}$ 和 ${c_2}$ 分别设置为1.4792, 最大加权因子 ${\omega _{\max }}$ 和最小加权因子 ${\omega _{\min }}$ 分别设置为0.9和0.4. 另外, DGPSO算法中, 多样性阈值设置为 $5 \times {10^{ - 6}}$ . 量子粒子群算法的参数选取如下: 种群大小M为42, 维数d为3, 种群范围控制在x (–100, 100), y (–100, 100), z (–50, 0), 最大迭代次数 ${t_{\max }}$ 设为2500次, 大量实验表明, $\;{\beta _0}$ 取值为1, $\;{\beta _1}$ 取值为0.5能得到较好的控制效果. 三种算法的适应度曲线如图6所示.

由图6可知, 针对DOA定位算法中, 运用基于QPSO的定位算法收敛效果比较好^[9,10], 其最小适应度值逐渐趋近于3左右; 而选用传统PSO和DGPSO算法两种方法, 所得到的结果, 其最小适应度值与QPSO差值较大, 会造成与真实炸点位置偏离甚远.

从图7所得结果表明, 采用传统PSO, 其定位误差平均为1.725 m, 采用改进的粒子群DGPSO分析进行定位, 其平均误差为0.920 m, 采用本文提出的QPSO算法进行DOA定位寻优, 平均定位误差可达0.324 m.

由此证明, 本文提出的基于QPSO的DOA震源定位方法行之有效, 可见该算法的准确性, 且有效提高了微震定位的精确度.

4 结论

为了解决传统的基于粒子群的DOA定位模型在地下浅层空间中定位误差大的问题, 本文创新性地提出一种基于QPSO的地下浅层震源定位方法研究, 该算法增大了搜索范围, 增强了粒子创造性, 摆脱了粒子运动受轨道的约束, 对定位精度的提升做出了重要的贡献.

实验表明, 由图7分析可知, 针对地下空间范围内的震源定位问题, 本文提出的定位算法, 其解算结果明显比其他两种PSO定位方法精度大幅度提高, 误差范围为0.324 m, 提高了定位精度, 经过实验仿真, 证明本文所提出的算法可以有效提高定位的精度.