桥梁裂缝的产生和发展往往体现桥梁的健康状态, 全面、尽早、准确地发现表面裂缝对桥梁安全运营具有重大意义. 传统上利用超声波、X射线、红外线等传感器来识别土木结构内部或表面是否存在裂缝, 它们本质上是点式传感器, 很难一次性测量出全尺度信息^[1,2]. 近年来, 基于布里渊时域分析(BOTDA)的光纤传感器被广泛应用^[3]. 分布式光纤传感器能够以厘米级的空间分辨率一次测量获取桥梁数百甚至上千米全尺度表面上的分布式应变. 在分布式光纤传感器所测得的分布式应变数据中, 裂缝区域会表现为异常, 通过检测分布式应变的异常来发现桥梁表面裂缝. 在测量过程中为了测量更多的应变细节, 通常会配置尽量小的空间分辨率, 所以测得应变数据的信噪比(SNR)较低, 导致源自裂缝损伤处的应变异常难以被发现^[4]. 在早期, 异常模式发现是基于概率统计模型来实现的^[5]. 使用统计学方法来实现异常检测必须要确定适合数据的分布模型, 设置模型参数, 但实际情况是, 往往无法知道数据集所遵循的标准分布类型, 或许数据本身就不服从任何的标准分布. 此外改进的基于距离的异常点检测算法、基于密度的局部异常点检测算法^[6–8]. 它们以欧氏距离作为异常评判标准, 但这两种方法在面对海量数据时, 计算复杂度高, 具有潜在的局限性. 随着模式识别领域中深度学习方法的迅速发展, 深度学习算法开始被应用到异常检测中来^[9], 如基于神经网络的方法, 此方法采用自适应学习算法对异常活动和非异常活动进行特征提取, 训练结束后提供待测数据进行异常检测^[10,11]. 此方法不需要对原始数据作统计假设, 有很好的抗干扰能力. 自动编码器(AutoEncoder, AE)是典型的神经网络之一, 它可以被看作是一个三层全连接网络, 具有出色的抗噪声特征表征能力^[12,13]. 但是当数据更加复杂时, 单层编码器无法有效的提取复杂数据的特征. 因此, Hinton等^[14]将多个AE逐层堆叠构成一个堆叠自编码器用于对高维数据进行降维和特征提取. 卷积神经网络是一类前向传播的神经网络, 通过若干个卷积核挖掘特征的局部相关性, 卷积神经网络实现了权值共享, 降低了深度神经网络的计算代价并且更易于训练^[15,16]. 卷积神经网络多被利用于处理图像, 但是最近的一些研究也将其引入到对序列数据的挖掘中^[17,18].

受此启发, 本文充分挖掘到自动编码器自动提取高质量特征表征的能力, 卷积神经网络可以利用多个卷积核提取多个特征. 所以, 结合自动编码器与卷积神经网络的优势, 本文提出一种基于一维堆叠卷积自编码器(Stacking Convolutional AutoEncoder, SCAE)的分类检测方法来处理低信噪比的分布式应变裂缝检测. 该方法首先将应变序列标准化后划分为等长的子序列, 所有的子序列可以分为两类, 一类是从存在裂缝的结构表面获得的裂缝应变子序列(CS), 另一类是从正常的结构表面获得的非裂缝子序列(NS), 然后利用SCAE对这些子序列进行自适应的特征提取, 最后将SCAE提取的特征作为Softmax分类器的输入来进行分类, 以达到检测的目的. 微小裂缝检测是基于CS/NS二元分类的结果实现的. 该方法在人为制造微小裂缝的15米工字钢梁上进行了验证.

1 模型与算法

本文设计的基于一维堆叠卷积自编码器的分布式应变裂缝检测过程的具体算法流程如图1, 图中数据预处理部分的虚线框表示子序列截取, 特征提取部分的椭圆虚线框表示池化窗口, 矩形虚线表示卷积核.

第1部分为数据预处理部分, 将分布式光纤传感器感测到的应变序列进行标准化, 使用滑动窗口将其截取为多个子序列, 作为第2部分的输入样本数据.

第2部分为特征提取部分, 此部分由一维堆叠卷积自编码器的3个卷积层(Conv)和3个池化层(Pool)构成, 用以提取输入子序列具有噪声鲁棒性和高分辨率特征, 并将其输入第3部分.

第3部分为分类部分, 将提取到的高分辨率的特征表征输入Softmax分类器, 得到两个概率, $p(crack|x)$ 表示当前特征表征判断为裂缝的概率, $p(noncrack|x)$ 表示当前特征表征判断为非裂缝的概率, 根据两个概率的大小, 来判断是否该子序列为裂缝.

1.1 数据预处理

本文首先采用模式识别中常用的z-score标准化方法对采集的分布式光纤应变数据进行标准化, 其公式为: ${\hat S^i}{\rm{ = }}\dfrac{{{S^i} - {\mu _i}}}{{\sigma _i}}$ , ${S^i}$ 是独立测量中的第 $i$ 个分布式应变序列. ${\mu _i}$ 为 ${S^i}$ 的均值; $\sigma _i$ 为 ${S^i}$ 的标准差. ${\hat S^i}$ 则为 ${S^i}$ 标准化后的数据.

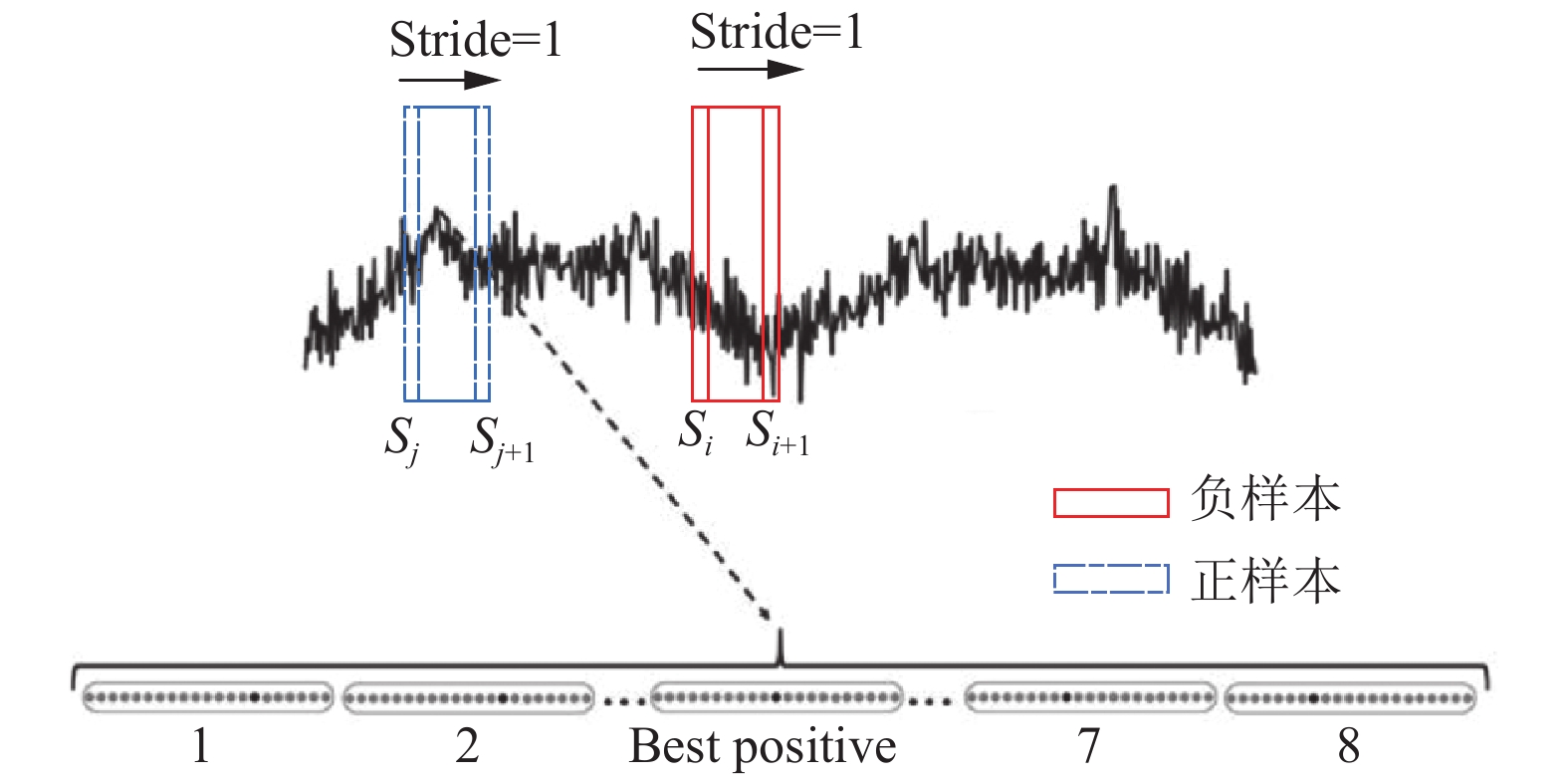
由于应变序列数据点与点之间并不独立, 很多异常都是存在于子序列中, 所以本文关注应变序列子序列的异常检测, 运用具有固定长度的滑动窗口, 把应变序列分为若干子序列进行异常检测, 该方法不仅能够观测单个数据点的异常情况, 还可对整个应变序列中所有子序列进行异常检测. 正样本选取以裂缝点{80, 200, 362, 482}为中心的样本视为最佳正样本, 步长为1, 滑动窗口大小为24, 将距离最佳正样本最近的7个样本标记为正样本, 其他数据全部标记为负样本. 具体的样本扩增情况图2所示.

1.2 一维卷积堆叠自编码器(SCAE)

自动编码器是一种无监督的神经网络模型, 它可以学习到输入数据的隐含特征, 这称为编码, 同时用学习到的新特征重构出原始输入数据, 称之为解码. 单层AE可以被认为是一个三层全连接神经网络, 分别为输入层, 隐藏层, 输出层. 卷积自编码器(Convolutional AutoEncoder, CAE)其核心思想是将AE中全连接网络换为卷积神经网络. 一维堆叠卷积自编码器由多个一维CAE分层堆叠而成, 前一个CAE编码器的输出为后一个CAE的输入, 第一个CAE的输入为预处理后应变子序列. 一维卷积自编码器可以获取噪声鲁棒性强, 可判别性高的特征, 主要是因为其模型堆叠起来的深层结构与单层自动编码器相比, 具有更强的特征表征能力. 每一层CAE的编码器对输入数据进行映射, 解码器对编码数据进行映射, 映射后的数据是输入数据的近似. 解码器和编码器同时训练, 不断的最小化重构误差, 得到最优模型. 此外其网络模型采用了卷积神经网络, 卷积神经网络相比于全连接网络的优势在于它采用了局部连接、参数共享、多个卷积核、池化. 局部连接主要是卷积层的节点和其前一层的部分节点相连接, 用来学习局部特征, 这种局部连接的方式减少了大量的参数数量, 加快了学习速率; 参数共享是指每一个卷积核在遍历整个数据时, 卷积核的参数不变, 这样的机制最大的作用就是很大限度地减少了运算量; 使用多个卷积核是因为一个核的参数是固定的, 其提取的特征也会单一化, 使用多个卷积核有利于提取多特征; 池化层其实是一个下采样的过程, 主要是为了降低维度并保留特征的有效信息, 减小过拟合, 同时提高模型的容错性.

图3是由两个CAE堆叠的SCAE模型, 其中 $X$ 为第一个CAE的输入, 其大小为 ${{w}} \times 1$ . 图中左边虚线框部分, 每一个卷积和池化表示一次CAE的编码过程. 其公式如下所示:

${h_{i,1}} = {s_f}(W \otimes {X_i} + b)$

(1)

${h_{i,2}} = {\rm{pool}} ({h_{i,1}})$

(2)

上式中, ${X_i}{\rm{ = }}{h_{i - 1,2}}(i = 1,2, \cdots, n)$ , 当 $i{\rm{ = }}1$ 时, ${X_i} = X$ . ${h_{i,1}}$ , ${h_{i,2}}$ 分别表示为第 $i$ 个编码器中卷积后的数据和池化后的数据, ${h_{i,2}}$ 也是第 $i$ 个编码器输出的特征; $ \otimes $ 表示卷积; $W$ 为卷积核, 其大小为 ${k_w} \times 1$ , 数目为 ${{{k}}_n}$ ; $b$ 为偏置向量; ${s_f}$ 为激活函数; ${\rm{pool}}$ 表示池化. 图中右边虚线框部分表示一次CAE的解码过程. 解码的具体过程如下:

${\hat h_{i,1}} = {s_{\rm{g}}}\left( {{{\hat W}_{i,1}} \otimes {h_{i,}}_2 + {{\hat b}_{i,1}}} \right)$

(3)

${\hat h_{i,2}}{\rm{ = upsample(}}{\hat h_{i,1}})$

(4)

${\hat X_i}{\rm{ = }}{s_g}{\rm{(}}{\hat W_{i,2}} \otimes {\hat h_{i,2}} + {\hat b_{i,2}})$

(5)

上式中, ${\hat X_i}$ 为输入 ${X_{{i}}}$ 的重构数据; ${\hat b_{i,1}}$ 和 ${\hat W_{i,1}}$ 为第 $i$ 个卷积自编码器解码过程中的第一个卷积的偏置和卷积核; ${\hat b_{i,2}}$ 和 ${\hat W_{i,2}}$ 为第 $i$ 个卷积自编码器解码过程中第二次卷积的偏置和卷积核, 其中 ${\hat W_{i,2}}$ 卷积核的数量为1, 因此最终重构出 ${\hat X_i}$ 的大小与输入 ${X_{i}}$ 一致; 上采样得到的特征为 ${\hat h_{1,2}}$ ; ${s_g}$ 是解码器中的激活函数, 与编码器中一致. 本文使用ReLu函数作为激活函数.

单层CAE模型的目标是最小化输入数据 ${X_i}$ 与重构数据 ${\hat X_i}$ 的误差, 其损失函数如下所示:

${L_1}({X_i},{\hat X_i}) = \left(\frac{1}{{2M}} {\sum\limits_{m = 1}^M {\left\| {{X_i}^m - {{\hat X}_i}^m} \right\|} ^2}\right)$

(6)

其中, $i$ 表示堆叠卷积自编码器中第 $i$ 个CAE, M表示训练过程中输入样本的总数.

1.3 Softmax分类器

Softmax是一个基于概率的多类分类器^[19]. 数据集 $\{ ({z_1},{y_1}),({z_2},{y_2}), \cdots ,({z_M},{y_M})\} $ 中共包含M个样本, 分为K个类别, 对于给定的输入样本 ${z_m}$ , Softmax分类器会基于式(7)判断属于每一类别的概率, 输出一个分类标签 ${y_m}$ .

${H_w}({z_m}) = \left[ {\begin{array}{*{20}{c}} {p({o_m} = 1|{z_m};w)} \\ {p({o_m} = 2|{z_m};w)} \\ \vdots \\ {p({o_m} = K|{z_m};w)} \end{array}} \right] = \frac{1}{{\displaystyle \sum\limits_{c = 1}^K {{e^{w_c^{\rm{T}}{z_m}}}} }}\left[ {\begin{array}{*{20}{c}} {{e^{w_1^{\rm{T}}{z_m}}}} \\ {{e^{w_2^{\rm{T}}{z_m}}}} \\ \vdots \\ {{e^{w_K^{\rm{T}}{z_m}}}} \end{array}} \right]$

(7)

其中, ${o_m}$ 是输入 ${z_m}$ 的输出类别; $w = {[{w_1},{w_2}, \cdots ,{w_K}]^{\rm{T}}}$ 是模型的参数, 需要通过训练数据来优化; $\dfrac{1}{{\displaystyle \sum\limits_{c = 1}^K {{e^{w_c^{\rm{T}}{z_{\rm{m}}}}}} }}$ 对概率分布进行归一化, 使得所有类别的概率和为1.

1.4 预训练和微调算法

用于二分类的一维SCAE和Softmax中的卷积核的权重和自由参数都是需要调整的. 本文采用预训练和微调来调整其参数. 预训练分为两个阶段, 第一个阶段是对堆叠自编码器中的3个CAE单独训练, 训练目标是最小化公式(6)中的损失函数. 第二阶段是将训练好的3个单层CAE以图3方式堆叠起来, 再对Softmax进行预训练. 通过最小化交叉熵函数L₂对其优化.

${L_2}(w) = - \frac{1}{M}\sum\limits_{m = 1}^M {\sum\limits_{j = 1}^K {\left( {1\left( {{{\rm{y}}_m} = j} \right)\log \left( {\frac{{{e^{w_j^{\rm{T}}{z_m}}}}}{{\displaystyle \sum\nolimits_{k = 1}^K {{e^{w_k^{\rm{T}}{z_m}}}} }}} \right)} \right)} } $

(8)

其中, M表示数据集中共包含M个样本, K表示类别, ${z_m}$ 为一维SCAE输出的第 $m$ 个子序列的特征, $w = $ $ {[{w_1},{w_2}, \cdots ,{w_K}]^{\rm{T}}}$ 为Softmax回归模型的自由参数. 在预训练之后, 对整个模型进行微调, 以重新优化SCAE中所有编码器以及Softmax分类器的自由参数. 本文中微调是将一维SCAE中各CAE编码器和Softmax作为一个整体去微调它们的自由参数. 通过最小化交叉熵函数L₃对其优化.

${L_3}(\Theta ) = - \frac{1}{M}\sum\limits_{m = 1}^M {\sum\limits_{j = 1}^K {\left( {1({y_i} = j)\log (H({X^m};\Theta ))} \right)} } $

(9)

整个模型为 ${o_i} = H({X^m};\Theta )$ , $\Theta $ 为模型中所有需要训练的的参数, ${X^m}$ 为输入的第 $m$ 个子序列.

2 实 验 2.1 实验数据

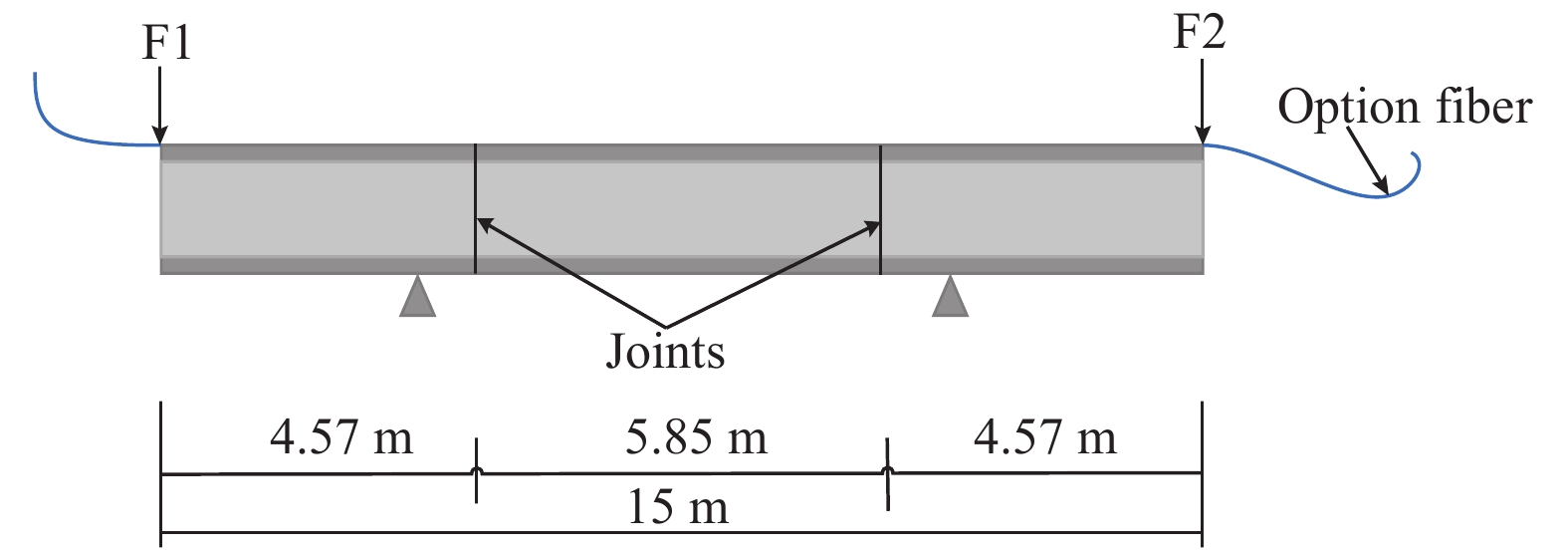
本文中使用的数据由实验室搭建试验台采集, 实验台由工字梁、分布式光纤应变传感器和光纳仪组成, 如图4所示.

工字梁钢结构由三段长度分别为4.575 m、5.85 m和4.575 m的工字钢拼接而成, 两个拼接接头处有张口宽度可调的人造裂缝, 通过在工字钢结构两端施加配重, 微小裂缝的裂缝张口宽度(COD)会相应的从0逐渐增加. 分布式光纤传感器一去一回平行地粘附在钢结构上表面, 由此每个裂缝被独立感测两次, 分布式应变数据呈现4个裂缝损伤.

本文中的分布式应变测量分为2个组, 设置为两个不同的空间分辨率(SR), 分别为10 cm和20 cm. 其中两个分组中又各分为5个case, 一共10个case, 每个case中独立测量20次, 具体测得的裂缝张口宽度见表1.

2.2 数据预处理

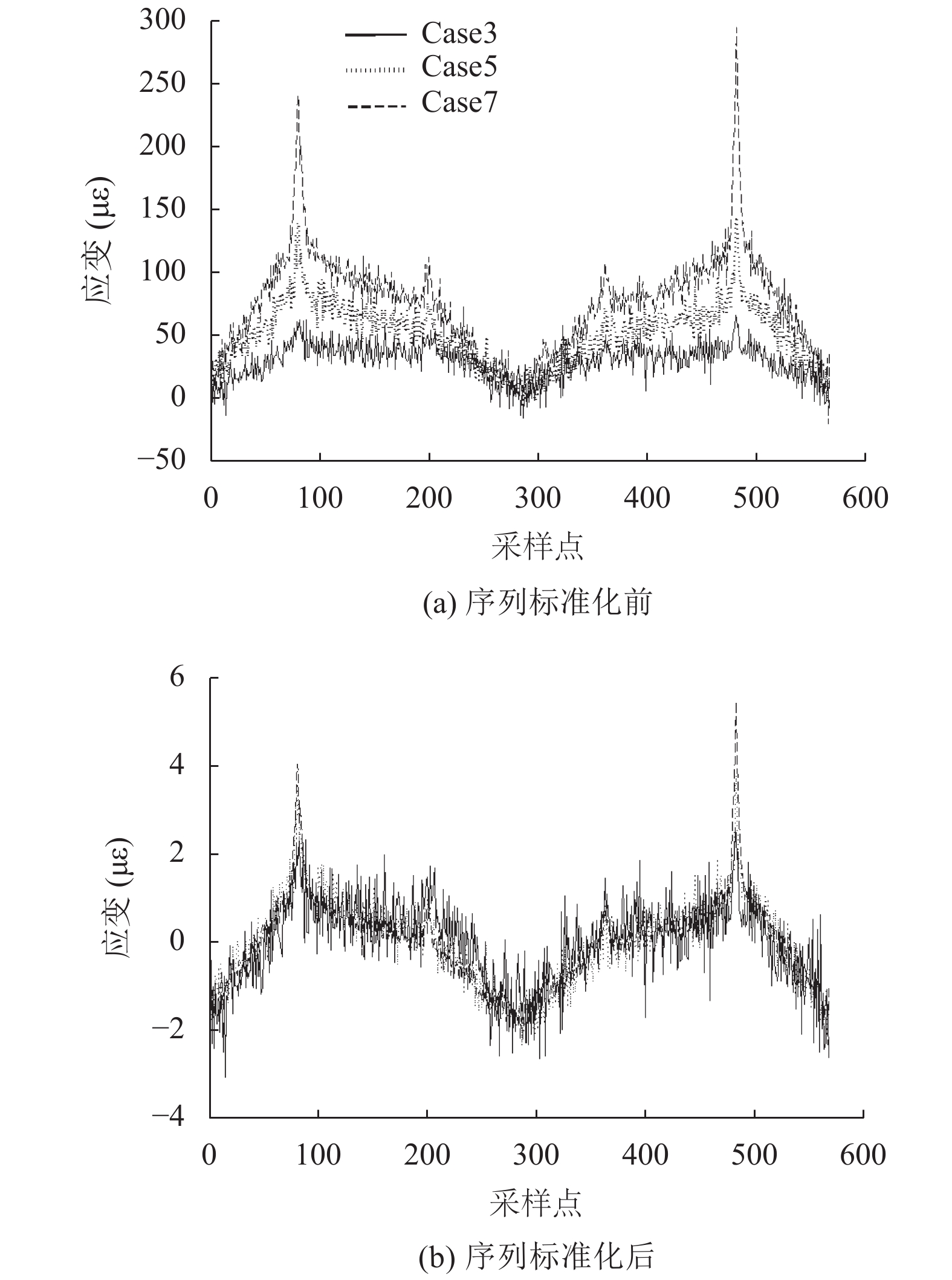
首先采用1.1节中z-score标准化方法对采集的数据进行标准化, 标准化后如图5所示, 图5(a)是分布式应变序列case3, case5, case7独立测量20条数据中的其中1条, 图5(b)是对3条应变序列标准化后的序列数据.

使用1.1节中样本扩增的方法对数据样本进行扩增, 经过数据样本扩增之后, 一共得到108 400个子序列样本, 其中正样本子序列有5120个, 负样本子序列有103 280个. 把扩增后子序列取40%作为训练集, 20%作为验证集, 40%作为测试集, 用于本文模型的训练、验证与测试.

2.3 模型参数设置

在模型中主要的参数设置如表2所示, 主要包括卷积自编码器中每个卷积层中的卷积核大小、卷积核数量以及步长. 池化层中池化窗口大小以及步长.

(1)输入为24×1的一维分布式应变子序列;

(2)网络共有3个卷积层, 其卷积核数目为分别为64、128和256, 卷积核大小均为 $3 \times 1$ , 卷积层中, 步长为1, 同时两侧进行大小为1的零填充, 因此每层卷积后的尺寸与输入尺寸相同;

(3)网络共有3个池化层, 每层使用平均池化, 池化窗口大小均为2×1. 池化层中, 步长为2, 因此每次池化后输出尺寸是输入尺寸的1/2;

(4)卷积后的特征要经过Flatten过程, 将得到的多特征图“压平”为一个一维序列. 将其输入Softmax分类器分类.

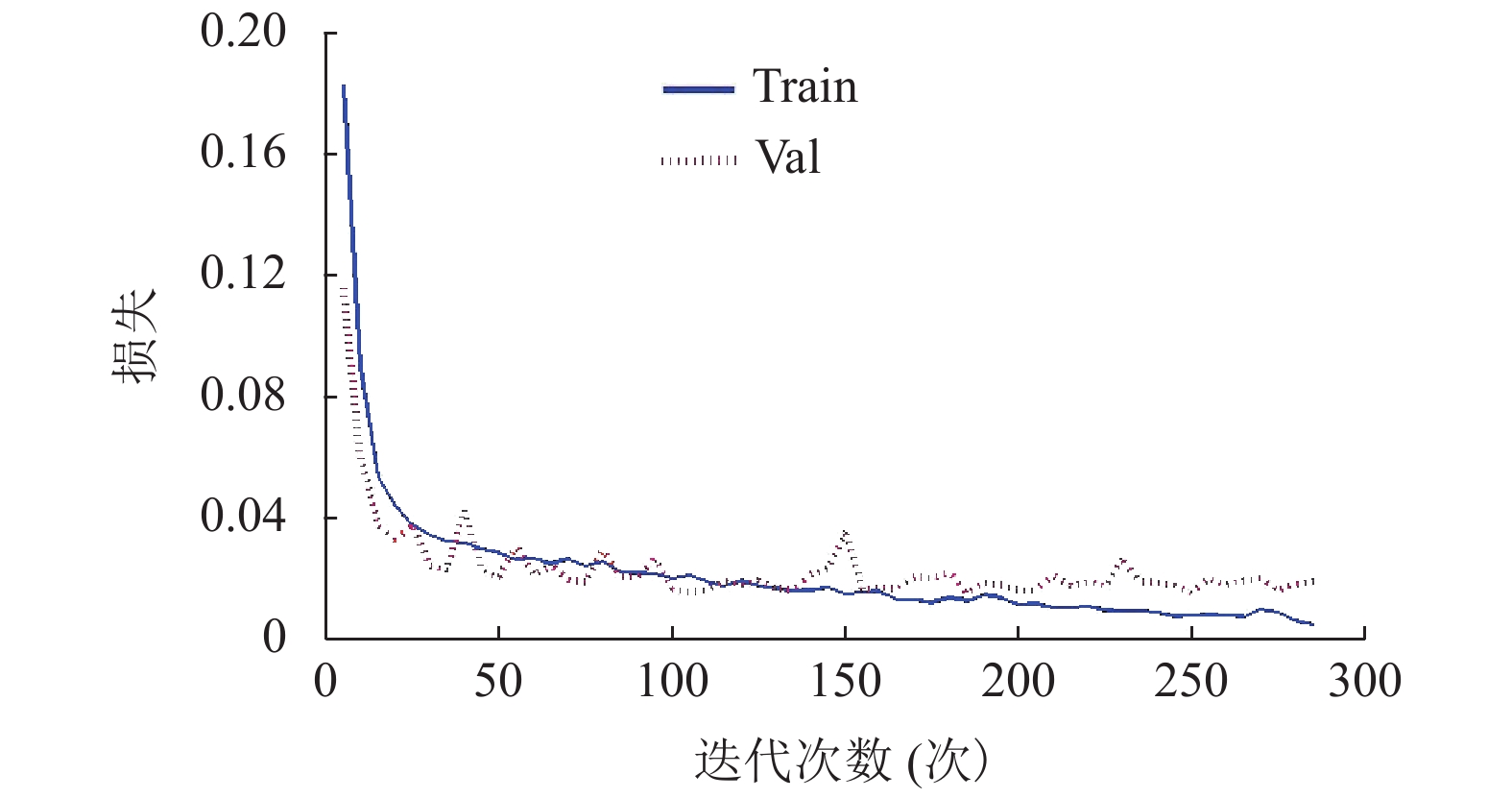
2.4 模拟钢梁实验结果及分析

预训练和微调两个过程都是通过最小化损失函数来得到最优自由参数. 预训练过程是单独调整各个CAE以及Softmax的自由参数. 微调是把SCAE 中各CAE编码器和Softmax作为一个整体去调整自由参数. 自由参数调整的准确性体现在迭代过程中, 损失不断降低, 趋于收敛时得到的自由参数是最优的. 图6是微调过程中, 训练集(train)和验证集(val)的损失变化曲线, 实线表示训练集的损失变化曲线, 虚线表示验证集损失变化曲线. 本文设置的微调迭代次数为400次, 从图中可以看出, 迭代240次后, 训练集和验证集的损失已经慢慢趋于稳定, 运用了早停法(early stopping)策略实际迭代288次, 保留迭代288次后的参数作为最优模型参数. 早停法是验证集在训练好的模型的表现, 当验证集连续迭代几次后, 损失增大, 停止训练, 这样就能避免继续训练导致过拟合的问题.

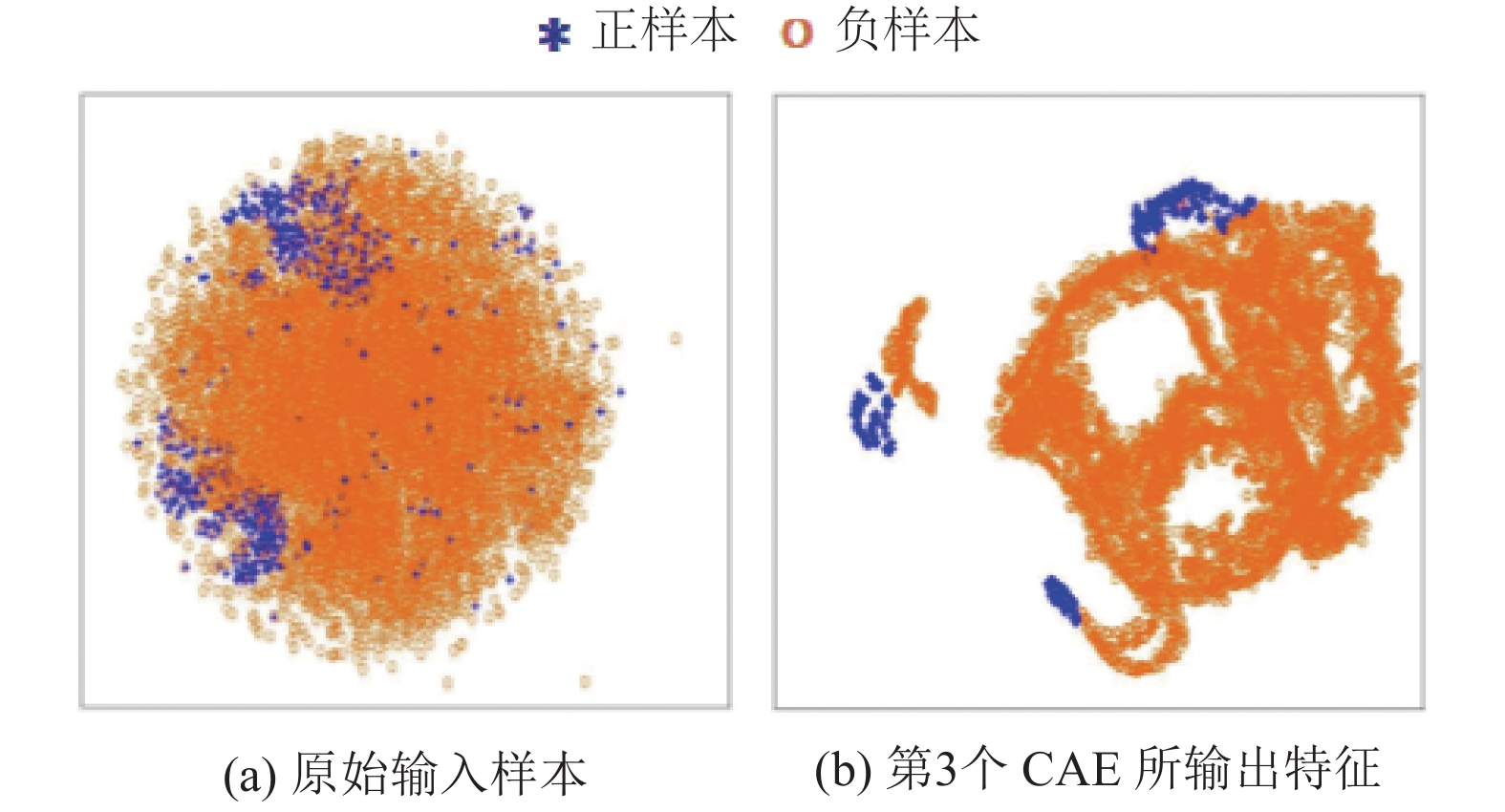
t-SNE算法是一种典型的降维和数据可视化的方法^[20,21]. 为了直观的看出一维堆叠自编码器模型参数调整的准确性以及在训练好的模型中所提取特征的可分辨性. 本文使用t-SNE算法将输出特征可视化到二维空间, 图7是t-SNE可视化图, 图中*是正样本, o是负样本, 图7(a)是对原始输入样本数据可视化, 可以看出, 正负样本混合在一起; 图7(b)是对一维堆叠卷积自编码器第3个CAE输出特征的可视化, 可以看出, 经过深层网络训练后, 正负样本的特征可辨识分离度变得明显. 因此, 所提出的基于SCAE的模型具有提取可识别特征的能力.

将测试集送入训练好的模型中进行分类检测. 为了说明本文方法相较于全连接网络的优势和预训练对检测结果的影响. 将本文方法与堆叠自编码器(SAE)和卷积神经网络(CNN)的检测结果进行了比较, 其比较结果如表3所示, 本文CNN的结构与SCAE的结构相同, 但在其训练过程中, 没有进行预训练的阶段只有对整体进行了微调. SAE是由3个AE堆叠起来, 在训练过程中, 对每一层AE进行预训练, 预训练的过程分为两个阶段, 第一个阶段是对每一层的AE独立训练, 优化参数. 第二个阶段对3个一维AE逐一训练后将AE堆叠起来, 并利用堆叠后隐藏层输出的特征对Softmax进行预训练. 最后对整体进行微调. 表中两种方法所使用的训练集、验证集以及测试集相同.

表3中FN为假阴性, 表示裂缝子序列被检测为非裂缝, FP为假阳性, 表示为非裂缝子序列被检测为裂缝, FP与FN出现的总和记为Error. Acc为准确率, 表示预测正确的样本的占总样本数的比重. 从表中可以看出本文方法准确率最高.

本文方法用于微小裂缝检测, 因此假阴性(FN)很重要. 从表中可以看出有22个裂缝子序列误检为非裂缝, 将分类后的结果定位到光纤应变序列. 当SR=10 cm时有16个检错的子序列出现的case3的第二和第三个裂缝部分, 有3个检错的子序列出现在case3的第四个个裂缝上, 有3个检错的子序列出现在case5的第二个个裂缝上. 其他的case中, 所有的裂缝子序列都被正确的检测. 当SR=20 cm时, 所有的裂缝都被正确的检测. 结果表明, 本文方法能够有效的检测微裂缝, 但性能受空间分辨率的影响.

3 总结

本文针对具有人为裂缝工字钢梁表面上的分布式应变, 提出了一种基于一维堆叠自编码器的微小裂缝检测方法. 该方法将裂缝检测当作一种二分类问题. 通过逐层堆叠3个CAE来构建深度SCAE模型, 利用该模型从分段的应变子序列中自动提取高质量判别性高的特征表征. 将Softmax附加至最后一个CAE后, 以特征表征作为输入, 对原始输入应变子序列做出分类决策. 实验结果验证了本文方法的有效性, 其检测性能受空间分辨率的影响, 当SR为20 cm时, 可以准确检测出23 μm及以上的微小裂缝, 取得好的检测效果. 但当SR=10 cm时, 因为数据信噪比较低, 对COD为23 μm的微小裂缝无法完全检测. 因此在未来的工作中探索如何消除空间分辨率对裂缝检测的影响是必要的.