2. 国网江苏省电力有限公司 电力科学研究院, 南京 210019;
3. 河海大学 计算机与信息学院, 南京 211100
2. Electric Power Research Institute, State Grid Jiangsu Electric Power Co. Ltd., Nanjing 210019, China;
3. College of Computer and Information, Hohai University, Nanjing 211100, China
在激烈的市场竞争中, 客户服务[1]己经成为企业在市场上面临的重要问题之一, 许多公司在近年迅速发展的趋势下, 己意识到客户服务的重要性: 让客户满意, 把满足客户需求作为一切工作展开的目标和中心. 结合企业各自不同的实际情况, 因地制宜地建立适合本企业的客户服务中心是现阶段摆在所有企业面前的重要问题. 良好的客户服务能够联系企业与客户之间的感情, 维护并营造企业良好的社会形象, 最终实现培养消费者对于企业和品牌忠诚度的长远目标. 目前, 企业的客服中心在客户服务和产品咨询上起着重要的作用, 但是企业需要为此承担相应的成本开销; 而且, 传统的人工服务方式不仅在客户服务质量上存在不足, 还增加了企业的运营成本.
针对传统人工服务方式服务质量层次低以及运营成本高昂的问题, 虽然传统的基于统计的方法应用广泛, 但存在着对前提条件要求过于严格或结果不够精确等诸多缺陷. 近年来, 为了弥补传统方法的不足, 人们将注意力转移到应用各种机器学习技术上来. 而目前将聚类分析技术应用到客户服务问题中的研究还很少[2]. 因此, 利用历史服务数据, 分析反馈问题的客户的关键特征, 通过聚类分析技术对客户进行类比, 挖掘出具有类似特征的客户群体, 对客户可能存在的问题早发现、早解决、早预防, 避免更多的客户产生类似诉求, 以实现主动服务, 从而提供更好的客户服务体验.
电力客户服务中心作为供电企业与电力客户交流的窗口, 不仅能够为电力客户提供优质便捷的服务, 而且能直接客观地反映客户用电问题[3]. 目前对在线坐席与客户服务工单数据的分析, 主要是数据分析人员依据坐席人员受理工单时勾选的业务类型, 进行统计汇总实现工单的分类分析. 该分类结果受坐席人员的主观判断影响大: 一方面不能及时、客观地反映散布在不同工单类型中的客户用电问题; 另一方面不能完整地反映用电客户的真实诉求, 更不能挖掘出客户产生诉求的真实原因. 因此在电力行业急需一种高效的方法对工单中隐藏的内容进行挖掘分析, 并为电力营销服务提供辅助决策.
众所周知, 电力是关系国计民生的重要基础产业, 是国民经济的重要组成部分. 电力企业具有规模经济特征, 与燃气、自来水、电信等类似, 在一般公共服务类企业中具有显著的代表性. 而客户服务工作作为电力企业的一项重要经营活动, 不仅关系到电力客户的切身利益, 也关系到电力企业的经营效益. 电力企业的客户服务问题的解决方案对于解决全行业的客户服务问题有着广泛适用性[4].
聚类分析技术是一种常见的数据分析工具, 其目的是把大量数据点的集合分成若干类, 使得每个类中的数据之间最大程度地相似[5], 而不同类中的数据最大程度地不同. 聚类分析作为一种有效的无监督分类方式, 在数学、计算机科学、统计学、生物学和经济学等领域得到了广泛的应用和关注, 为深层次分析提供了技术支持和解决方案[6].
本文主要研究了将聚类分析技术应用在电力客户用电问题分析领域, 通过一系列的数据预处理技术以及改进的聚类分析方法, 对供电服务过程产生的工单信息进行挖掘分析. 文中基于数据挖掘中的聚类技术, 以电力客服中心获取的客户用电问题为数据基础, 建立客户服务数据分析模型, 进而提出了针对用电问题分析的改进的聚类算法. 最后通过实验验证了该方法可快速准确地实现客户服务数据的自动聚类, 挖掘出隐藏的客户用电问题关键信息, 从而为改进电力客服质量与潜在服务风险预测提供了数据支撑.
本文内容安排如下: 第1节对客户用电问题的经典应用场景以及被动服务(事件驱动)和主动服务(服务驱动)两种情况进行了详细说明. 第2节概括了数据预处理的方法, 构建了聚类分析模型和算法. 第3节对省级电力客户服务工单数据进行了聚类分析, 并对实验结果作了评估与比较. 第4节阐述了聚类分析模型在实际应用场景中的应用方案.
1 用电问题分析电力企业客户服务, 是以电力客户需求为导向, 包括对电力客户服务前、服务中和服务后的一切活动, 是一个全员、全过程的系统工作. 近年来, 随着电力消费需求变化的加快, 对电力客户服务前, 通过客户历史服务数据, 分析产生用电问题的客户的关键特征, 通过聚类分析技术对客户进行类比, 挖掘出潜在具有类似特征的客户群体, 在客户产生用电问题之前就主动为客户提供服务, 达到防患于未然的目的越来越迫切.
这些潜在客户群具有极高的可能发生相同的用电问题, 当潜在客户通过微信公众号发起咨询时, 首先抽取出在线客户的关键特征, 而后通过聚类的方法挖掘出有类似特征的其他客户曾经发生过哪些用电问题, 以此来类比该用户可能想要提出的用电问题. 提高客户服务的效率, 从而辅助客服提升在线服务能力.
根据用电问题的产生情况不同, 可将类比分析分为被动服务(事件驱动)的类比分析和主动服务(服务驱动)的类比分析两种情况. 对于因某小区大批量初装用户、举行促销活动、中介恶意查询、系统故障(缴费未到账)、出现极端天气等因素导致某类用电问题的用户达到一定数量或一定比例的需要被动进行类比分析的场景, 可通过分析产生该类用电问题的客户的关键特征, 挖掘出具有类似用电问题的客户群体, 可以辅助客服提升在线服务能力. 对于定期发起的如电费账单出账、线路系统升级改造、安全隐患定期排查等需要主动进行类比分析的场景, 可通过分析群体客户的历史服务数据, 挖掘出可能受影响的客户群体, 可以辅助电力公司提升主动服务能力, 而且此类场景还可以用于群体客户服务风险预测与排查. 较为典型的应用场景包括:
(1) 串户场景: 当某个抄表段号一个月内由于串户问题, 发起的客服咨询达到了4个及4个以上, 则需要进行客户用电问题类比分析, 分析整个段号内是否存在同样具有串户风险问题的客户, 对其进行事先提醒, 避免串户问题的发生.
(2) 电费异常场景: 当某个区域一个月内有4户及4户以上客户由于电费异常来进行咨询, 则需要进行客户用电问题类比分析, 分析整个区域内是否存在其他当前月用电量远超以往的客户, 对其进行事先提醒, 提醒客户检查家用电器是否故障, 避免产生经济损失.
(3) 频繁停电场景: 当某个区域两个月内超过3户(包括3户)客户发生停电, 则需要向电力公司内部业务员提醒, 提醒其该区域可能存在设备故障问题, 需要安排人员进行停电原因排查.
(4) 欠费复电场景: 在客服系统中自动查询断电客户, 判断其是否已经缴纳电费, 如已经缴纳电费, 自动通知业务员尽快在24小时内恢复通电, 如客户未缴纳电费主动向客户发送信息, 提醒客户及时缴纳电费以恢复通电, 避免造成不必要的损失.
以上电力企业客户服务问题场景都可以通过聚类分析技术, 对电力客户群体依据用电问题的关键特征进行聚类, 以挖掘出潜在的具有相似用电问题特征的客户群. 常见客户用电问题如表1所示.
| 表 1 常见客户用电问题 |
上述应用场景中的业务流程如图1所示.

|
图 1 应用场景业务流程图 |
图1中描述的流程如下: 先将客户用电问题95598工单历史数据库与在线坐席访客咨询数据库进行关联以得到客户用电问题历史服务数据集, 利用客户用电问题历史服务数据集训练聚类分析模型, 然后依据主动触发条件或者被动触发条件将电力客户群体送入聚类分析模型, 发掘潜在具有相似用电问题特征的电力客户群体.
2 模型构建与算法设计 2.1 数据预处理通常, 客户服务信息的数据格式为一张二维表, 每一行为一个用户服务记录. 表结构中包含若干属性, 其属性值涉及各种数据类型, 以文本字符串居多.
2.1.1 缺失值处理通过调研发现此类数据中往往会出现许多属性值为空的情况. 其原因在于: 记录的属性是预定义的, 可用于完整描述客户服务中所有可能出现的特征; 而在一个具体的客户服务中, 某些属性所对应的特征可能根本没有出现, 从而导致缺失[7]. 所以对这些缺失值的处理, 也是数据分析过程中的关键环节. 通常, 对缺失数据的处理有两种方式: 用属性的均值来填补, 或者直接删除缺失数据. 在对于服务数据缺失值的处理上, 可以分情形采用不同的方式. 如果缺失值所占比例较低且为数值类型, 则可通过均值来填充; 反之, 如果缺失值所占比例较高, 则可认为对应属性所描述的为非公共特征, 采用直接删除的方法是较为合理的.
2.1.2 冗余处理客户服务数据内容往往较为繁杂, 数据内部存在冗余. 而且, 还可以根据实际需求对数据进行降维, 通过缩小数据规模使实验更为高效. 客户服务数据一般是由若干条记录所构成的一张二维表, 每一行为一条记录, 记录的每个分量为一个属性值, 对应某个属性. 这些属性的集合构成一个记录结构. 不妨将此类结构化数据中的最小语义单位称为语义原子. 为了给出冗余处理的方法, 以下先给出记录结构、语义块及极小语义覆盖的定义, 然后给出相应的求解极小语义覆盖的算法, 从而实现冗余处理[8].
定义1. 一个记录结构R是一个有限集, 其中任一元素e∈R称为一个属性, 而一个属性则是若干语义原子的集合.
定义2. 令e为记录结构R中的一个属性, e的语义基He是e中包含的所有语义原子的集合, 记录结构R的语义基HR是R的所有属性中所包含的语义原子的集合, 即
定义3. 令R为一个记录结构, 如果ParR={B1, …, Bn}, 满足Bi
定义4. 令R为一个记录结构, ParR为R的一个语义划分, B∈ParR. 如果
以一个例子来说明上述概念. 假设记录结构R的若干个属性中有3个用于描述地址信息, 分别是**省、**市、**市**区/县, 则可将这三个属性划分为属性块B1={**省, **市, **市**区/县}, 则属性块B1语义基为HB1={**省, **市, **区/县}. HB1中的语义原子为**省、**市、**区/县. B1属性块的一个极小语义覆盖为{**省, **市**区/县}.
通过语义划分得到属性块, 根据需求删除没用的属性块, 对保留的属性块求极小语义覆盖. 求极小语义覆盖的具体流程如下.
输入: 属性块B
输出: B极小语义覆盖
1)初始化一个空集
2)从B中找出一个属性e, e需满足集合
3)判断
在数据的操作中, 针对不同的地址数据, 采用转换到统一坐标系下的方式, 方便对数据进行处理与分析. 地址数据在原数据中通常以文字说明的形式呈现, 为了保留原数据的语义信息并切实表现数据之间的语义差异, 对原数据的地址信息进行地理编码. 地理编码是将地址信息映射到地理坐标的过程, 其中地理坐标用地理经纬度信息表示, 这样原地址数据转换为两个维度信息: 经度信息和纬度信息[9].
图2所示为通过地理编码后的地址信息表现为两维信息, 通过逆地理编码可将这两维信息还原为客户地址.

|
图 2 地理编码与逆地理编码 |
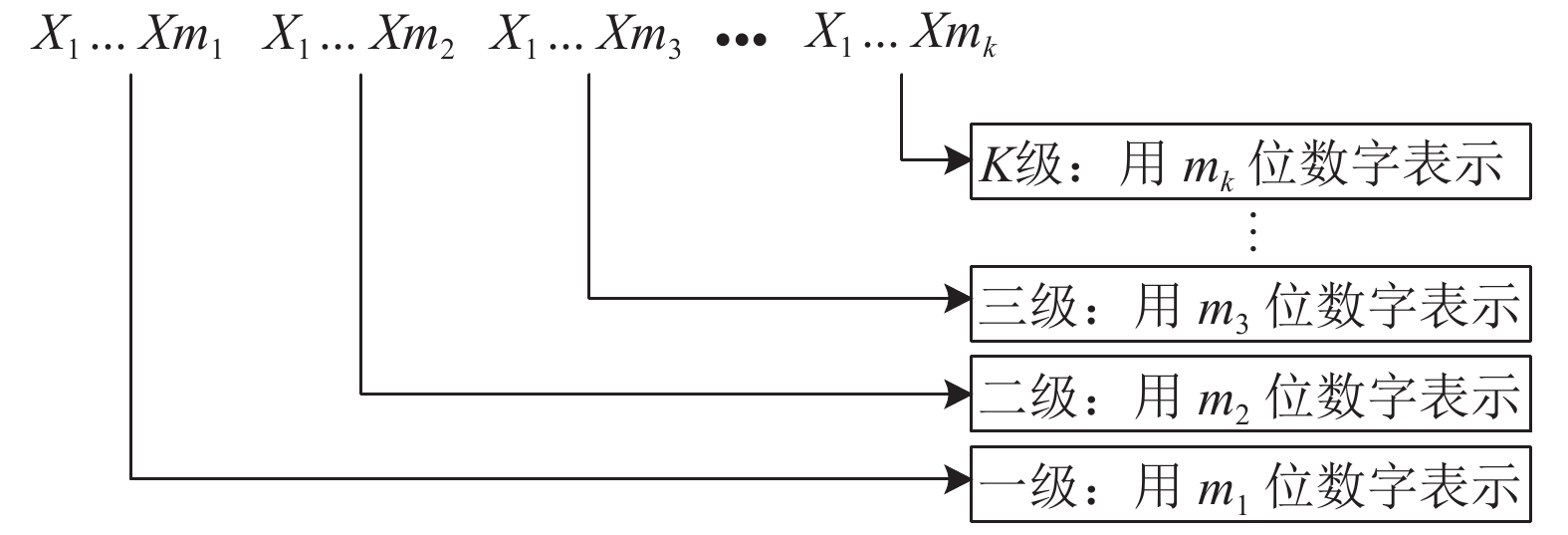
在数据操作过程中, 不同属性之间存在从属关系, 则可以参考邮政编码和身份证地址码采用K级M位编码规则[10], 如图3所示.
图3中的X代表占位符, 每级采用若干位数字表示, 每级的实际位数由该层级的类别数目决定, 实际位数等于该层级类别数目的位数. 因此K级M位编码规则中的M满足: M=m1+m2+m3+…+mk.
|
图 3 K级M位编码规则 |
2.2 算法设计 2.2.1 原始K-Means算法原理
K-Means算法是一种实现简单、应用广泛的聚类算法, 以平均值作为聚类中心, 簇内点尽可能紧密, 簇间距离尽量大. K-Means算法首先要选取初始聚类中心, 并对所有数据点进行分类, 之后根据每个聚类的平均值来调整聚类中心, 循环迭代直到确定的中心点不再改变[11]. 目的是使各个类内包含对象相似性最大, 类间对象相似性最小. 算法流程如下.
输入: 聚类的簇数K和包含N个样本的数据集
输出: K个聚类簇, 使平方误差准则最小
1) 从N个样本中选择K个样本, 作为初始聚类中心.
2) 计算其余样本到各聚类中心的距离, 将其分配到距离最短的距离中心对应的类别中.
3) 更新聚类中心: 将每个类别中所有样本所对应的均值作为该类别的聚类中心, 计算目标函数的值.
4) 判断聚类中心和目标函数的值是否发生改变, 若不变, 则输出结果; 若改变, 则返回步骤2).
大小为n的数据集, 指定的聚类数为k, 样本的维数为k, 则进行一次迭代的计算时间由三部分组成: 将每一个样本归到离它最近的聚类中心, 需要时间O(ndk); 新的类产生后, 计算新的聚类中心所需的时间O(nd); 计算聚类成本函数所需时间O(nd); 而迭代次数则由数据集大小、聚类数以及数据分布情况决定, 算法总的时间复杂度为O(ndk)[12].
2.2.2 肘部法则通常, 使用肘部法则求K-Means聚类最佳分类数K. K-Means算法运行过程中会不断地移动类中心点, 也就是重心, 把类中心点移动到该中心点包含样本的位置的平均值, 然后重新划分其内部成员[13]. K-Means虽然可以自动分配样本到相应的类, 但是不能决定要划分出多少个类. K-Means的参数为类的重心位置和其内部观测值的位置. K-Means参数的最优解能够使成本函数值最小. K-Means成本函数公式如下:
| $ J = \sum\limits_{k = 1}^k - {\sum\limits_{i \in {C_k}} {\left| {{x_i} - {\mu _k}} \right|} ^2} $ | (1) |
式中, μk表示第k个类的重心位置. 类的畸变程度为类重心与类内部成员位置距离的平方之和, 成本函数为所有类畸变程度(distortions)之和. 由成本函数知, 如果类内部的成员分布越紧凑, 那么类的畸变程度越小; 反之, 如果类内部的成员分布越分散, 那么类的畸变程度越大. 因此, 要求出使成本函数最小化的参数, 就需要重复配置每个类s包含的观测值, 并不断移动类重心直到求出为止.
肘部法则的核心思想是: 随着簇数k的变大, 数据集的划分会变得精细, 每个簇的聚合程度会逐渐提高, 那么成本函数值会逐渐变小. 如果k小于实际的聚类数时, 那么k的变大会大幅提高各个簇的聚合程度, 成本函数值的下降幅度也会很大; 而当k等于真实聚类数时, 再增加k所得到的聚合程度的提高会迅速变小, 成本函数值的也会随之大幅下降, 之后伴随k值的继续变大而趋于稳定, 也就是说成本函数值和k值的关系图会呈现出手肘形状的曲线, 而这个肘部对应的k值就是数据的真实聚类数[14].
2.2.3 改进的K-Means算法针对客服工单数据中存在较多孤立点, 对聚类分析结果产生巨大影响的情况下, 本文对传统K-Means算法进行改进, 使改进后的K-Means算法更加适用于客户工单类数据的分析.
当簇内样本是密集的, 而簇间区别明显时, 表明K-Means算法效果显著. 对于处理大数据集, K-Means算法依然高效, 复杂度为O(nkt), 其中t是迭代的次数. 但是, K-Means算法也存在局限性, 它只能在聚类样本的平均值被定义时才可以执行, 且无法适用于需要处理符号属性的数据. K-Means算法对初始聚类中心与样本的输入顺序较为敏感, 对于与不同的输入顺序, 聚类结果往往会有较大差异. 因为算法使用迭代更新的方法, 所以当初始聚类中心在局部值最小附近时, 算法比较容易得到局部最优解.
要进行聚类的初始数据大多都存在孤立点, 即存在较少数据点距离数据密集分布区域较远的情况. 因为算法首先随机地选取若干样本作为初始聚类中心, 所以此时可能存在将孤立点选为初始聚类中心的情况, 这种情况会严重影响聚类效果. 此外, 在聚类运算过程中, 会将聚类均值点(类中心中所有样本位置的平均值)作为新的聚类中心进行聚类. 孤立点会导致新的聚类中心偏离数据密集区, 使聚类效果变差. 因此, 孤立点的存在会对K-Means算法的聚类效果产生很大的影响[15]. 所以, 改进算法首先进行查找并排除孤立点, 然后才可以进行聚类.
为排除孤立点, 减少孤立点对聚类的影响, 可以先计算初始数据集中各个样本之间的距离, 将每个样本与其他样本距离之和求出, 删除距离之和最大的点. 可以根据精确度的要求, 删除若干个距离之和较大的样本, 这样可以极大地减少孤立点对聚类的影响. 查找并排除基于距离之和的孤立点时, 算法将进行N平方次的样本间的距离计算, 当N增大时, 计算量将几何倍的增长. 为了减少计算量, 先用代价很小的粗聚类方法进行聚类, 再根据每个粗聚类簇内的样本个数按比例均匀抽出若干样本, 抽出的样本可以代表粗聚类簇, 这些抽出的样本分布在样本空间各个角落, 这样抽出的样本比直接从数据集内均匀抽取的样本更具代表性, 因此这些抽出的样本可以有效地代表原数据集. 此时, 不需计算每一样本与原始数据集中其他样本的距离, 只需计算样本与抽出的对象的距离, 正常抽取的样本数量较少, 所以算法的复杂度将极大地降低.
此外, 为提高K-Means聚类算法在客户服务工单数据分析中的准确率, 使用了一种自适应特征权重的K-Means聚类算法. 该算法首先计算属性的均方差来选取初始聚类中心, 根据迭代结果, 按照类内紧密、类间远离的原则调整属性在距离公式中的特征权重, 这样能使数据点在欧氏空间中的真实距离更加明显, 也使用本文所用到的客户服务工单数据对算法的有效性进行验证[16].
将n个m维待聚类样本表示为如下的矩阵形式:
| $X = \left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}&{ \cdot \cdot \cdot }&{{x_{1m}}} \\ {{x_{21}}}&{{x_{22}}}&{ \cdot \cdot \cdot }&{{x_{2m}}} \\ { \cdot \cdot \cdot }&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot } \\ {{x_{n1}}}&{{x_{n2}}}&{ \cdot \cdot \cdot }&{{x_{nm}}} \end{array}} \right]$ |
为使不同属性上的数据具有可比性, 也为了方便计算属性贡献度, 将上述矩阵按维度归一化至[0.01, 1]. 设当前迭代后将n个对象划分为K个聚类, 每个聚类中的对象个数分别为: n1, n2, …, nk, 则所有K个聚类在第j维属性上的类内距离之和为:
| $ {d_n} = \sum\limits_{k = 1}^K {\sum\limits_{i = 1}^{{n_k}} {{{({x_{ij}} - {m_{kj}})}^2}} } $ | (2) |
式中, mkj为聚类k在第j维属性上的均值. 所有K个聚类在第j维属性上的类间距离之和为:
| $ {d_w} = \sum\limits_{k = 1}^K {{{({m_{kj}} - {m_j})}^2}} $ | (3) |
其中, mj为数据集在第j维属性上的均值. 根据当前迭代结果, 计算属性j对聚类的贡献度: cj=dw/dn. 类内紧凑、类间远离通常用来度量聚类的整体性能. 对单个属性而言, 如果聚类的结果在该属性上满足类内紧凑且类间远离的原则, 则表明该属性区分对象的能力强, 对聚类的贡献大; 反之, 则表明该属性区分对象的能力弱, 对聚类的贡献小. 第j维属性的特征权重为:
| $ {w_j} = {c_j}/\sum\limits_{j = 1}^m {{c_j}} \begin{array}{*{20}{c}} {}&{{w_j} \in \left[ {0,1} \right], \displaystyle\sum\limits_{j = 1}^m {{w_j} = 1} } \end{array} $ | (4) |
使用上式修正欧氏距离公式, 得到加权的欧氏距离公式:
| $ d(m,n) = \sqrt {\sum\limits_{j = 1}^m {{w_j}{{({x_{mj}} - {x_{nj}})}^2}} } $ | (5) |
属性的特征权重可以根据属性的贡献度预先设定. 属性的特征权重越大, 就说明该属性对聚类越重要, 在欧氏空间中该属性的坐标轴就会产生较大拉伸; 反之, 说明该属性对聚类不重要, 欧氏空间中该属性的坐标轴就会产生较大缩减. 属性权重的设定有两种特殊情况: 一种是所有属性的权重都相同, 此时便是传统的聚类方法; 另一种是属性权重为零, 即为不考虑, 可排除此种属性影响.
为验证改进K-Means聚类算法的有效性, 在Python环境下, 对传统K-Means、基于信息熵的固定权重K-Means聚类算法及改进K-Means聚类算法的有效性进行检验, 比较不同聚类算法的性能.
首先选取UCI上的鸢尾花数据集说明改进算法对权重的调整过程. 该数据集共有4个属性, 其中petal length和petal width两个属性对聚类结果影响较大.
用传统K-Means算法连续运行10次, 其平均迭代次数为7.3次, 基于信息熵的固定权重K-Means算法迭代次数为5次, 改进K-Means聚类算法经过4 次迭代后收敛, 说明改进K-Means聚类算法能够显著减少迭代次数. 改进K-Means聚类算法对鸢尾花数据集各属性特征权重的调整情况如图4所示.

|
图 4 鸢尾花特征权重调整曲线 |
由图4可知, 随着迭代的进行, 算法能够自动识别属性的重要性, 重要属性的特征权重逐步增大, 次要属性的权重不断减小, 最终petal length和petal width两个属性的权重由最初的0.25分别调整为0.4314和0.4731. 这种动态调整反映了各属性对类内紧密、类间远离聚类结果的重要程度, 能够更真实地反映对象在欧氏空间中距离, 减小距离失真程度, 有利于提高聚类性能.
3 基于电力工单数据的实验及结果分析每年的电力客户服务工单数据存在相似性, 因此数据选取一年范围内的服务工单, 而一年中受天气因素的影响, 四个季度之间的服务工单数据差距较大, 每个季度3个月份之间的差别较小, 因此数据选取以一年跨度中的每个季度中最具代表性的月份, 即2017年8月、2017年11月、2018年2月和2018年5月的省级所有服务工单为数据基础, 并在关联工单和在线坐席访问数据后, 从客户用电问题内容出发进行了挖掘分析, 处理的工单记录数共计35 000条.
3.1 电力数据预处理实验数据主要来自电力服务工单数据, 结合调研结果以及冗余处理的方法, 针对风险预测业务场景的需求, 总结出八维属性包括供电单位、地市、区县、客户地址、工单类型、业务类型一级、业务类型二级、业务类型三级. 但是属性值主要为文本, 因此需要对工单数据进行数值化操作.
考虑到邮政编码和身份证地址码都存在不同区共用一个编码的问题, 对于地市、区县采用三级六位编码制, 前两位表示省, 第三四位代表地市, 最后两位代表区县, 对全省各地市区县进行数值化编码. 供电单位编码规则类似采用三级六位编码制, 前两位表示省, 第三四位代表地市, 最后两位代表区供电单位.
电力服务工单数据中的工单类型、业务一级、业务二级、业务三级的编码规则采用四级四位编码制, 第一位代表工单类型, 第二位代表业务一级, 第三位代表业务二级, 第四位代表业务三级.
电力服务工单数据中的客户地址采用转换到统一坐标系下的形式, 每个地址对应二维数据, 分别代表经度和纬度.
3.2 最佳聚类数预处理后的数据利用手肘法选取最佳聚类数k. 具体做法是让k从20开始取值直到取到你认为合适的上限(一般来说这个上限不会太大, 这里选取上限为30), 对每一个k值进行聚类并且记下对应的SSE (误差平方和), 然后画出k和SSE的关系图, 最后选取肘部对应的k作为最佳聚类数. 画出的k与SSE的关系图如图5所示.

|
图 5 SSE与k的关系图 |
显然, 肘部对于的k值为23, 故对于这个数据集的聚类而言, 最佳聚类数应该选23.
3.3 评估方法K-Means是一种非监督学习, 不像监督学习的分类问题和回归问题, 无监督聚类没有样本输出, 也就没有比较直接的聚类评估方法. 但是可以从簇内的稠密程度和簇间的离散程度来评估聚类的效果. 常见的方法有轮廓系数Silhouette Coefficient[17]和Calinski-Harabasz Index[18]. 本实验采用Calinski-Harabasz Index方法, 这个方法计算简单直接, 得到的Calinski-Harabasz分数值
Calinski-Harabasz分数值
| $ s(k) = \frac{{tr({B_k})}}{{tr({W_k})}}\frac{{m - k}}{{k - 1}} $ | (6) |
其中, m为训练集样本数, k为类别数. Bk为类别之间的协方差矩阵, Wk为类别内部数据的协方差矩阵, tr为矩阵的迹.
也就是说, 类别内部数据的协方差越小越好, 类别之间的协方差越大越好, 这样的Calinski-Harabasz分数会高.
3.4 实验结果利用改进的K-Means算法对预处理后的数据进行聚类分析, 并采用Calinski-Harabasz Index方法对聚类的结果进行打分, 结合之前肘部法则推算出的最佳k值, 实验让k从20开始取值直到取到29, 实验结果如表2所示.
| 表 2 改进K-Means算法聚类结果得分 |
用Calinski-Harabasz Index评估的k=23时候聚类分数为, 可见k=23的聚类分数比其他都要高, 这也符合预期. 预处理后的数据为维度为9, 当特征维度大于2, 无法直接可视化聚类效果时, 用Calinski-Harabasz Index评估是一个很实用的方法.
根据改进K-Means算法聚类分析结果的Calinski-Harabasz Index评估得分数画出曲线图可以更加直观的看出实验聚类分析结果, 曲线图如图6所示.

|
图 6 Calinski-Harabasz Index得分曲线图 |
当k值取23时改进K-Means算法聚类分析得出23个簇中心如表3所示.
| 表 3 改进K-Means算法得出的23个聚类簇中心 |
表3中每一行代表一个聚类簇中心坐标, H1至H9分别代表供电单位、地市、区县、客户地址经度、客户地址维度、工单类型、业务类型一级、业务类型二级、业务类型三级对应的坐标.
簇中心1至簇中心23分别代表的用电问题如表4所示.
| 表 4 聚类簇中心 |
通过将各个簇中心业务类型、业务分级的数值与事先约定的编码规则对照, 可以得到具体的用电问题, 从而降低服务风险. 以簇中心6为例, 该位置有较多的客户进行投诉, 反应抢修服务超出时限. 该模型可以实时导入新的数据, 实现对簇中心的实时调整以应对新的服务风险的出现.
3.5 结果分析K-Means算法作为一种常用的聚类算法, 对球状分布的数据具有很好的效果, 但是算法对初始聚类中心敏感, 容易受到孤立点的影响. 文中在聚类之前排除了孤立点的影响, 提出了一种新的选取初始聚类中心的方法. 针对客服工单数据中存在较多孤立点, 对聚类分析结果产生巨大影响的情况下, 文章对传统K-Means算法进行改进, 使改进后的K-Means算法更加适用于客户工单数据.
分别利用原 K-Means算法和改进后的 K-Means算法进行聚类分析对比, 聚类结果如表5所示.
实验结果表明, 改进算法更接近实际数据分布. 虽然需要查找少量孤立点, 会增加时间消耗, 但是改进算法准确度较高, 聚类效果较好.
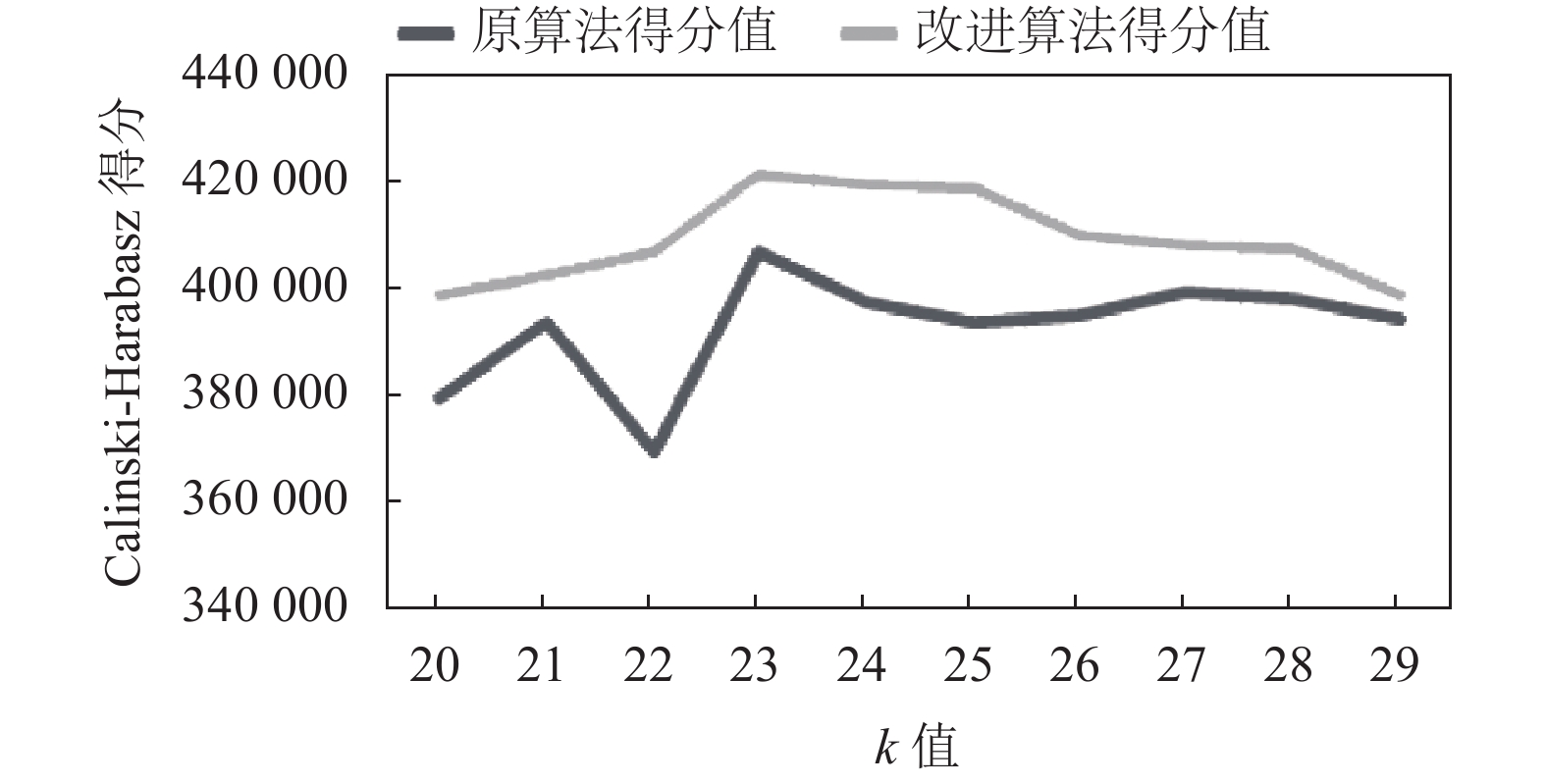
为了更加直观的表现改进算法的优越性, 根据经典K-Means算法和改进后的K-Means算法的聚类结果分析对比表画出曲线对比图, 如图7所示.
通过两者的聚类结果分析对比曲线图可以很明显的看出改进后的K-Means算法Calinski-Harabasz得分更高, 聚类效果更好, 更加准确挖掘出潜在具有相同问题的电力客户.
| 表 5 原算法和改进后算法的Calinski-Harabasz分值对比 |
|
图 7 聚类结果分析对比曲线图 |
比较每一条聚类结果是否和真是的结果一致, 计算聚类结果的准确率(Accuracy), 如式(7)所示.
| $ acc = \frac{{{N_{\rm {cor}}}}}{N} $ | (7) |
其中, N表示工单总数, Ncor表示正确聚类的工单数. 改进后的K-Means聚类模型准确率高达91.2%. 而采用传统的聚类算法模型, 准确率只有85.7%. 通过验证认为, 改进后的K-Means模型能从工单数据出发, 较为精准地将具有相同问题的电力客户聚类.
4 结论针对客户服务数据的特征, 本文给出了一种改进的K-Means聚类算法. 应用该算法可以从大量工单数据中找到若干个簇中心, 以挖掘出客户服务中的用电问题, 不仅为改进客服服务质量提供数据支撑, 还能为潜在服务风险的预测奠定数据基础, 从而让相关企业为客户提供更优质的服务.
以电力工单数据分析为例, 根据用电问题产生情况的不同, 可将类比分析分为被动服务(事件驱动)的类比分析和主动服务(服务驱动)的类比分析两种情况.
(1) 对于因大批量初装用户、举行促销活动、中介恶意查询、系统故障(缴费未到账)、出现极端天气等因素导致某类用电问题的用户达到一定数量或占一定比例的业务场景, 则可施行被动服务类比分析, 将发生该类问题的客户服务工单数据, 作为改进K-Means算法的输入, 进行聚类分析, 从而得到代表着该类用电问题的簇中心. 当再次接入新的客户时, 可以通过计算新客户与该类问题簇中心的欧式距离来判定潜在的风险: 若新客户在簇类内, 则客户是该类问题的潜在风险客户, 若客户在簇类外, 则客户发生该类问题风险较小. 因此, 改进的算法可以预先判断客户是否具有发生该类问题的风险, 从而提前实施相应的措施.
(2) 对于定期(每月、每周或每天)发起的如电费账单出账、线路系统升级改造、安全隐患定期排查等业务场景, 则可以采用主动服务类比分析, 将存在多种用电问题的客户服务工单数据, 作为改进的聚类算的输入, 从而得到代表前N个最频繁出现的用电问题的簇中心. 以此数据为支撑, 再结合业务处置的历史经验, 可做出相应的日常风险预判. 比如, 该方法还可以通过对往年同期数据的聚类, 挖掘出高概率发生的具体用电问题的信息包括时间和地点等, 通知相关部门做好预防措施; 再如, 通过对实时工单数据的聚类, 可以挖掘出突发问题, 从而能及时通知相关部门前往验证并解决突发问题, 与此同时通知出现电力问题区域的客户, 让客户知晓当前的情况, 以减少投诉, 减轻客服压力.
值得一提的是, 该方法还可以应用到其他相关行业的客服系统, 以提升客户服务质量.
| [1] |
谭火超. 关于完善电力客户服务、提升供电服务质量的探讨. 机电信息, 2018(33): 174-175. DOI:10.3969/j.issn.1671-0797.2018.33.100 |
| [2] |
Kruppa J, Ziegler A, König IR. Risk estimation and risk prediction using machine-learning methods. Human Genetics, 2012, 131(10): 1639-1654. DOI:10.1007/s00439-012-1194-y |
| [3] |
邹云峰, 何维民, 赵洪莹, 等. 文本挖掘技术在电力工单数据分析中的应用. 现代电子技术, 2016, 39(17): 149-152. |
| [4] |
陈璐. 浅谈电力公司的电力营销信息系统的建设. 电子世界, 2014(22): 208. DOI:10.3969/j.issn.1003-0522.2014.22.200 |
| [5] |
Hartigan JA, Wong MA. Algorithm AS 136: A K-means clustering algorithm. Journal of the Royal Statistical Society. Series C (Applied Statistics), 1979, 28(1): 100-108. |
| [6] |
Michie MG. Use of the Bray-Curtis similarity measure in cluster analysis of foraminiferal data. Journal of the International Association for Mathematical Geology, 1982, 14(6): 661-667. DOI:10.1007/BF01033886 |
| [7] |
Rahman G, Islam Z. A decision tree-based missing value imputation technique for data pre-processing. Proceedings of the Ninth Australasian Data Mining Conference. Ballarat, Australia. 2010. 41–50.
|
| [8] |
Bechtel W, Shagrir O. The non-redundant contributions of marr’s three levels of analysis for explaining information-processing mechanisms. Topics in Cognitive Science, 2015, 7(2): 312-322. DOI:10.1111/tops.12141 |
| [9] |
Rushton G, Armstrong MP, Gittler J, et al. Geocoding in cancer research: A review. American Journal of Preventive Medicine, 2006, 30(2S): S16-S24. |
| [10] |
Guo XJ, Song ZX. To study on coding for identity card of citizen and its application. Value Engineering, 2007, 26(10): 114-116. |
| [11] |
Zhang ZQ, Yang QY, Dou A. An improved K-means algorithm for reciprocating compressor fault diagnosis. Proceedings of 2018 Chinese Control and Decision Conference. Shenyang, China. 2018. 276–281.
|
| [12] |
Jain AK, Murty MN, Flynn PJ. Data clustering: A review. ACM Computing Surveys, 1999, 31(3): 264-323. DOI:10.1145/331499.331504 |
| [13] |
Appelboam A, Reuben AD, Benger JR, et al. Elbow extension test to rule out elbow fracture: Multicentre, prospective validation and observational study of diagnostic accuracy in adults and children. BMJ, 2008, 337: a2428. DOI:10.1136/bmj.a2428 |
| [14] |
Crozier SN, Falconer DD, Mahmoud SA. Least sum of squared errors (LSSE) channel estimation. IEE Proceedings F- Radar and Signal Processing, 1991, 138(4): 371-378. DOI:10.1049/ip-f-2.1991.0048 |
| [15] |
Mahmud S, Rahman M, Akhtar N. Improvement of K-means clustering algorithm with better initial centroids based on weighted average. Proceedings of International Conference on Electrical and Computer Engineering. Dhaka, Bangladesh. 2012. 647–650.
|
| [16] |
Tsai CY, Chiu CC. Developing a feature weight self-adjustment mechanism for a K-means clustering algorithm. Computational Statistics & Data Analysis, 2008, 52(10): 4658-4672. |
| [17] |
Aranganayagi S, Thangavel K. Clustering categorical data using silhouette coefficient as a relocating measure. Proceedings of the International Conference on Computational Intelligence and Multimedia Applications. Sivakasi, Tamil Nadu, India. 2007. 13–17.
|
| [18] |
Łukasik S, Kowalski PA, Charytanowicz M, et al. Clustering using flower pollination algorithm and Calinski-Harabasz index. Proceedings of 2016 IEEE Congress on Evolutionary Computation. Vancouver, BC, Canada. 2016. 2724–2728.
|
 2020, Vol. 29
2020, Vol. 29



