在精密机械行业, 微型摆轮(图1)是一种常见的部件, 在生产过程中容易出现表面不平整, 边缘处弧度不达标等缺陷. 因此, 在组装设备之前必须进行严格检测, 剔除次品. 传统的检测方法主要是人工检测, 工人通过双目显微镜放大零件图像, 并手动吹气来转动零件, 肉眼观察零件上下摆动幅度, 以确定零件是否合格. 人工检测依赖个人经验, 主观性强, 且易疲劳, 导致产品质量管理的不稳定, 难以量化评估. 采用视觉技术进行检测是大势所趋, 其能有效保证产品检测的准确度和稳定性.

一个优质的机器视觉系统必须具备以下几点: 第一, 所采用的光学系统必须成像清晰, 对比度好, 噪声少; 第二, 算法必须精确的计算出零件的边缘线; 第三, 算法必须具有一定的鲁棒性, 比如能够自动矫正倾斜的图像.

数字图像的基本单位是像素. 为了提高检测的精度, 需要进行亚像素的定位. 亚像素边缘检测是指将边缘附近的像素进行分解, 从而精确定位边缘^[1]. 常用的亚像素检测技术有矩法, 最小二乘方差法, 插值法, 拟合法等^[2,3]. 文献[2,4–6]提出了基于二次曲线拟合的亚像素定位模型, 该模型在理想条件下定位精准度高. 文献[7]提出了对二次多项式的最小二乘拟合求梯度的亚像素插值算法, 但模型比较复杂, 求解速度慢. 本文参考了以上文献中的理论, 使用一种基于局部区域特征的二次曲线模型来计算亚像素位置, 这种模型考虑了局部的特征和边缘梯度, 精确度高, 速度快, 能够满足项目的需要.

1 项目总体设计 1.1 光学方案设计

由于零件本身微小, 且检测的是轮面的平整度, 同时为了减少虚影提高图像对比度, 所以选择平行背光源. 镜头选择高分辨低畸变的远心镜头.

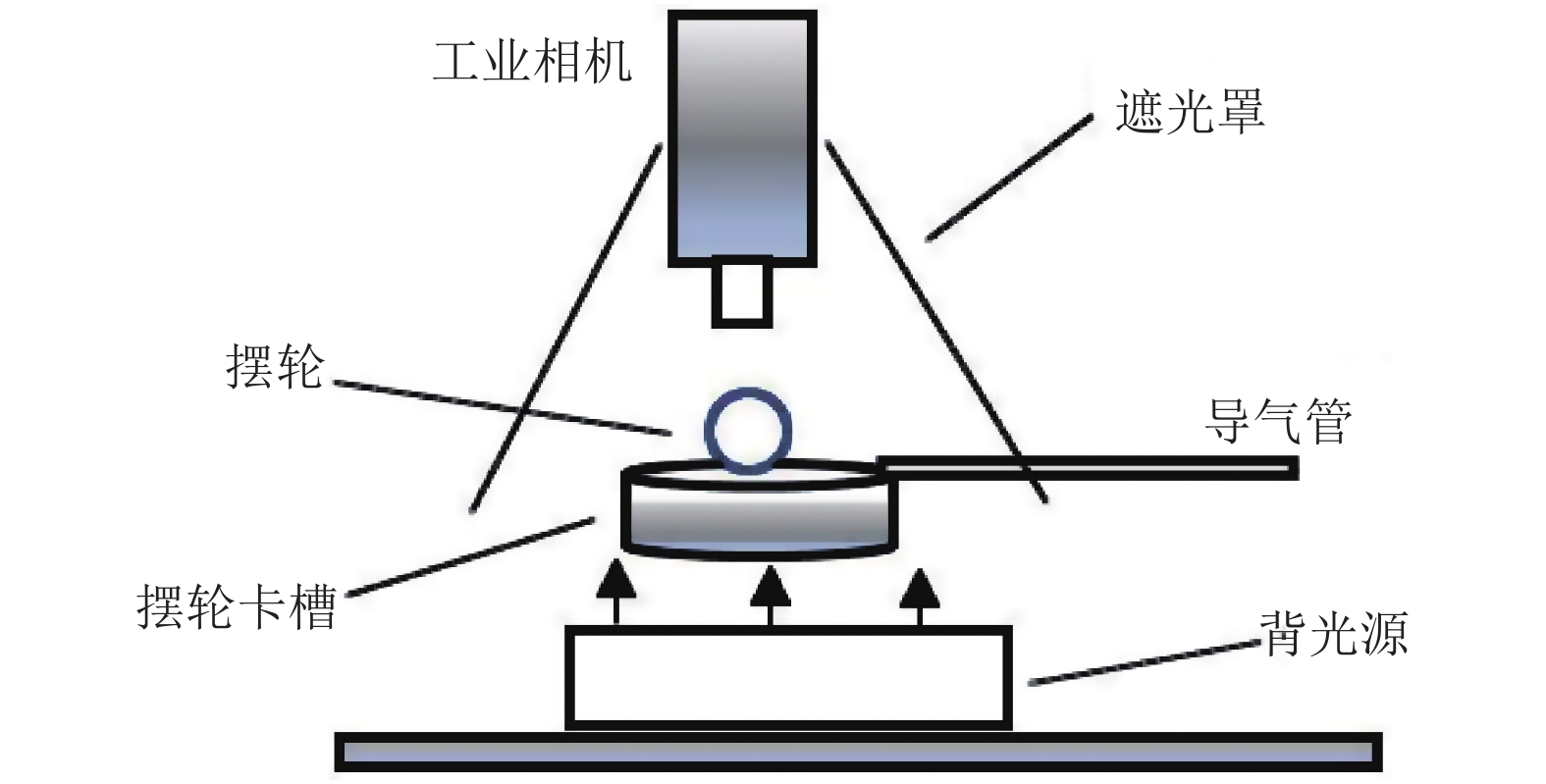
系统采用视频检测方式, 零件放置在专用的工作台上, 使用导气管吹动零件转动. 工作台如图2所示.

1.2 算法框架

摆轮检测依次经历如下步骤: 图像采集与预处理, Canny边缘检测, 倾角矫正, ROI (感兴趣区域)亚像素位置计算, ROI水平边缘和垂直边缘计算, 计算极差, 判定结果. 图3显示了这个流程框架.

2 算法分析 2.1 图像采集和预处理

图像采集是将传感器检测到的图像信息传输到计算机的过程. 摆轮图像中背景为白色, 目标为黑色, 目标和背景的对比度明显, 使用常见几种阈值分割方法进行实验, 实验结果如图4所示.

从上面的实验结果来看, OTSU方法, 迭代阈值法, p参数法效果都不错. p参数法依赖于参数的设置, 固定的参数会使得算法的鲁棒性降低. OTSU在细节体现上比迭代阈值法更好一些, 故选择OTSU法.

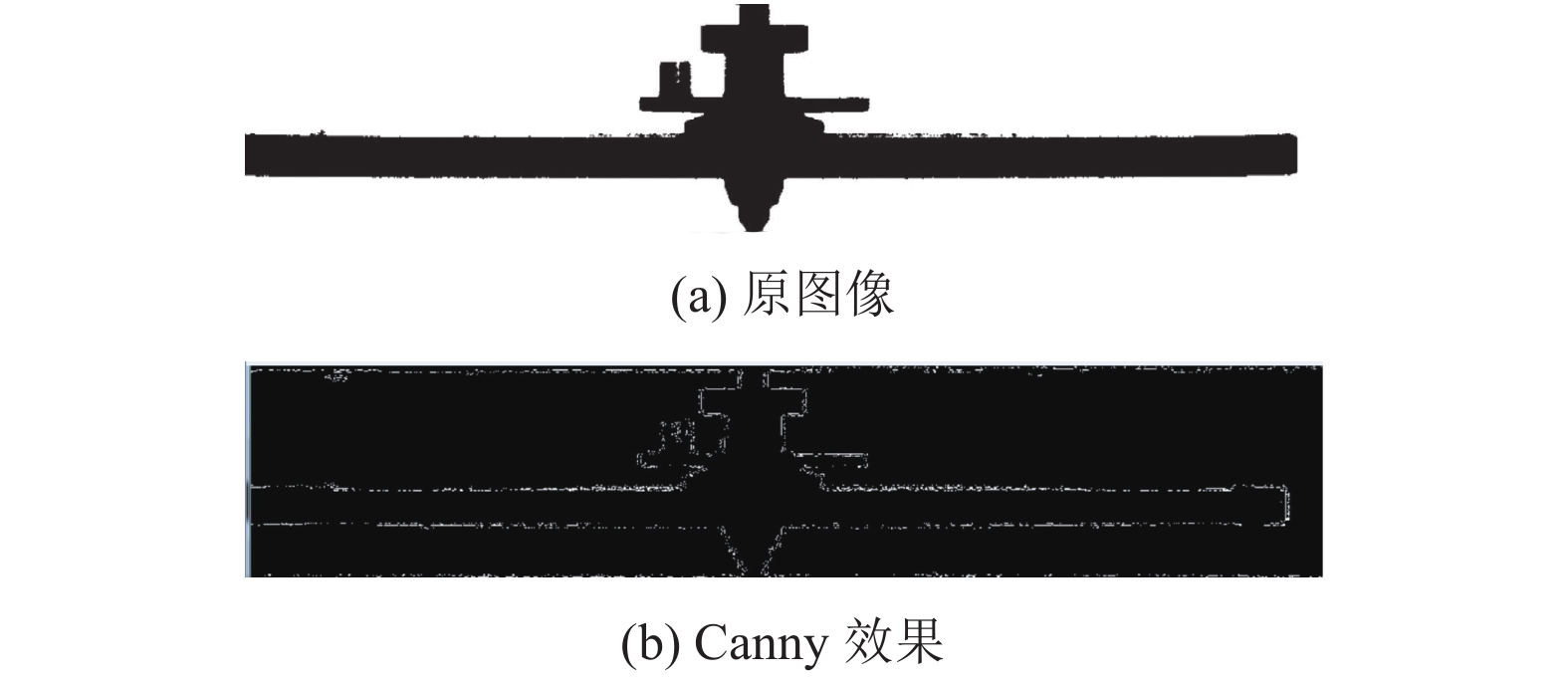
2.2 Canny边缘检测

图像的边缘检测算法有很多, 常见的有Robert, Sobel, Prewitt, Krisch, LOG, Canny等算子^[8]. 使用Canny算子检测的效果如图5所示.

Canny算法能够满足项目需要, 且使得后面霍夫直线检测时取得比较好的性能, 所以选择Canny算子.

2.3 图像矫正

零件在拍摄的过程中容易存在一定的倾斜, 根据先验知识, 倾斜的角度一般在30度以内. 目前常用的倾角矫正方法有: 基于投影的方法、基于Hough变换、基于线性拟合等方法^[9]. 使用霍夫变换的方法能够矫正摆轮图像的倾斜, 满足项目的需求. 下面是常见的两类倾斜情况及其矫正结果, 如图6所示.

从上面的实验结果可以看到, 利用霍夫直线检测算法能够矫正常见的沿顺时针或逆时针具有一定倾斜角度的图像.

2.3.1 图像矫正流程

1)基于Canny检测后的图像使用霍夫变换方法检测图像中的直线. 霍夫变换本身比较耗时, 但根据摆轮图像的特点只需要检测出2到3条比较长的水平直线, 其余水平直线和垂直直线则全部忽略掉. 当设置直线检测阈值为500像素点时即可达成上述目标. 这样能大大提高霍夫算法的效率.

2)对于每条检测出的直线, 获取其倾角θ, 如图7所示.

当 $\theta \in \left[ {\dfrac{\pi }{2}, \dfrac{{3\pi }}{4}} \right] \cup \left[ {\dfrac{{5\pi }}{4}, \dfrac{{3\pi }}{2}} \right]$ 时认为是水平直线倾斜后的结果, 属于其他区间时忽略掉. 统计这些直线的倾角并取其平均值作为最终的图像倾角α.

3)旋转图像至水平位置. 设β为图像需要旋转的角度, 则有:

$\beta = \alpha - \dfrac{\pi }{2}$

(1)

图像旋转的步骤如下:

第1步, 把图像坐标系的原点从左上角转移到图像中心.

第2步, 旋转所有像素点.

第3步, 把旋转后的图像平移到原来的图像坐标系中.

2.4 ROI亚像素计算

在该项目中我们使用了5×3的模板, 考虑每个可能的边缘像素, 然后在模板区域内计算一个二次曲线模型, 利用此模型计算亚像素位置. 二次函数模型是在一次函数模型的基础上推导出来的, 所以先介绍一次函数模型.

2.4.1 一次函数模型

如图8所示, 假设直线L: $y = kx + b$ 是图像中的边缘, 且L将图像区域分成上下两部分, 分别记做M, N. 这两部分的面积记做S_M, S_N, M, N也表示M, N两部分的平均灰度值. 直线L所在的坐标系的中心点为 $\left( {i, j} \right)$ . 设 $\left( {i, j} \right)$ 处像素的灰度值为 $F(i, j)$ , 它也代表整个模板区域的平均灰度值. 设图像区域总面积为S^[2,5]. 则有:

$S = {S_M} + {S_N}$

(2)

$ F(i,j) = \dfrac{{N \cdot {S_N} + M \cdot {S_M}}}{S} $

(3)

我们考虑中间像素 $\left( {i, j} \right)$ 的5×3邻域模板, 以L2、M2和R2来表示模板中直线L下侧左、中、右列的像素面积, 如图9所示. 直线L坐标系中心的位置依然是 $O\left( {i, j} \right)$ , l列中心的横坐标是i–1, r列中心的横坐标是i+1; 最上一行的中心纵坐标是j+2, 最下一行中心位置的纵坐标是j–2; 设每个像素格的边长为w^[2,5].

$ L2 = \displaystyle\int_{ - \tfrac{{3w}}{2}}^{ - \tfrac{w}{2}} \left(kx + b + \dfrac{5}{2} w\right){\rm d}x = \left(\dfrac{5}{2} - k\right){w^2} + bw $

(4)

$ M2 = \displaystyle\int_{ - \tfrac{w}{2}}^{\tfrac{w}{2}} \left(kx + b + \dfrac{{5w}}{2} \right){\rm d}x = \dfrac{5}{2}{w^2} + bw $

(5)

$ {{R}}2 = \displaystyle\int_{\tfrac{w}{2}}^{\tfrac{{3w}}{2}} \left(kx + b + \dfrac{{5w}}{2}\right){\rm d}x = \left(\dfrac{5}{2} + k\right){w^2} + bw $

(6)

设5×3模板中左边一列的像素灰度值之和为T_l, 中间一列为T_m, 右边一列为T_r, 则有:

${T_l} = \sum\limits_{J = j - 2}^{j + 2} {F(i - 1, J)} $

(7)

代入式(3), 可得:

${T_l} = 5N + \dfrac{{M - N}}{S}\sum\limits_{j - 2}^{j + 2} {{S_M}} $

其中, $ \displaystyle\sum {{S\!_M}} = L2, $ 所以, 可得:

${T_l} = 5N + \dfrac{{M - N}}{S}L2$

(8)

同理, 可知:

$ {T_m} = \sum\limits_{J = j - 2}^{j + 2} {F(i, J)} = 5N + \dfrac{{M - N}}{S}M2 $

(9)

$ {T_r} = \sum\limits_{J = j - 2}^{j + 2} {F(i + 1, J)} = 5N + \dfrac{{M - N}}{S}R2 $

(10)

2.4.2 二次函数模型

一次函数可以看做是二次函数当二次项系数为0时的特例, 所以使用二次函数模型来预测亚像素的位置会比一次函数模型更普遍一些. 在二次函数模型中我们还可以求得边缘的曲率, 这样对边缘的描述会更准确. 二次函数模型预测亚像素位置如图10所示. 各数学符号还保持前面的定义, 假设抛物线f : $y = a{x^2} + bx + c$ 为图像中的边缘.

边缘下侧左、中、右部分面积计算^[2,4–6]:

$ L2 \!=\! \int_{ - \tfrac{{3w}}{2}}^{ - \tfrac{w}{2}} \left(a{x^2} \!+\! bx\! +\! c\! +\! \dfrac{{5w}}{2} \right){\rm d}x\!=\! \dfrac{{13}}{{12}}a{w^3} + \left(\dfrac{5}{2} - b\right){w^2} + cw $

(11)

$ M2 = \displaystyle\int_{ - \tfrac{w}{2}}^{\tfrac{w}{2}} \left(a{x^2} + bx + c + \dfrac{{5w}}{2} \right){\rm d}x = \dfrac{1}{{12}}a{w^3} + \dfrac{5}{2}{w^2} + cw $

(12)

$ {{R}}2 \!= \! \displaystyle\int_{\tfrac{w}{2}}^{\tfrac{{3w}}{2}} \left(a{x^2} \!+\! bx \!+\! c \!+ \!\dfrac{{5w}}{2} \right){\rm d}x \!=\! \dfrac{{13}}{{12}}a{w^3} + \left(b + \dfrac{5}{2}\right){w^2} + cw $

(13)

由前面的推导过程可知, 式(8), (9), (10)在二次函数模型中依然成立. 将式(11), (12), (13)代入式(8), (9), (10)中, 可以得到包含了a, b, c三个变量的三个方程, 解之, 可得a, b, c的值.

$a = \dfrac{{{T_l} + {T_r} - 2T{}_m}}{{2(M - N)}} $

(14)

$b = \dfrac{{{T_r} - T_l}}{{2(M - N)}} $

(15)

$ c = \dfrac{{2{T_m} - 5(M + N)}}{{2(M - N)}} - \dfrac{1}{{12}}a $

(16)

由式(16)可知, 二次函数模型下真实的像素点(i, j)对应的亚像素位置为(i, j–c).

在上面的公式中, M, N代表了边缘两侧平均灰度值, |M–N|则代表了边缘两侧的梯度幅值, 其方向为边缘的梯度方向.

如图11所示, 设点O(i, j)处沿x方向的偏导数为f_x, 沿y方向的偏导数为f_y, 当 ${f_x} \cdot {f_y} > 0$ 时, 设 $\Delta {{x}} = 1$ ; 当 ${f_x} \cdot {f_y} \le0$ 时, $\Delta {{x}} = - 1$ .

$ M = \dfrac{1}{2}\left[ {F(i,j + 2) + F(i + \Delta x,j + 2)} \right] $

(17)

$N = \dfrac{1}{2}\left[ {F(i - \Delta x,j - 2) + F(i,j - 2)} \right] $

(18)

将式(17), 式(18)代入前面的公式, 即可求得二次函数模型下的亚像素位置.

在使用上述模型之前必须先粗略定位出边缘的位置. 对于每个边缘点, 使用上述模型求解亚像素位置.

2.5 计算边缘直线

如图12所示, 我们需要描绘出ROI中摆轮边缘的直线. 此处ROI就是方框的区域. 可以使用投影法来生成直线. 投影法是通过计算图像在水平和垂直边缘上的像素点的个数来确定边缘的位置^[10].

计算水平直线的方法如下. ROI中以行为单位, 每行的像素数累计起来, 相当于往y轴上投影, 按照式(19)的方式进行统计. $f(i, j)$ 为 $(i, j)$ 处的像素值. 为了利用计算前面得到的亚像素位置, i, j的增量都设置为0.5像素, 即将1个像素点分解为4个亚像素点, 这样就可以将边缘精确到0.5像素.

$Hi = \sum\limits_{j = 0}^{\Delta x} {f(i,j)} $

(19)

其中, 当 $f(i, j) > 100$ 时, $f(i, j) = 1$ , 当 $f(i, j) \le100$ 时, $f(i, j) = 0$ , Δx是ROI在x轴方向的长度.

在图12中, 从上往下依次是白色区域, 黑色区域, 白色区域, 所以生成的Hi数组从上往下会依次出现峰, 谷, 峰, 取靠上的峰值处的纵坐标y₀为生成的水平线段L1的起点P1的纵坐标, L1的终点P2的纵坐标也取y₀, P1, P2的横坐标取ROI的沿x轴方向的起点和终点的横坐标, 连接P1, P2即得到水平线段L1. 如图13所示.

生成边缘垂直线的方法与上面生成水平线的方法类似. 只是在计算ROI投影时, 以列为单位, 统计每列的像素数, 相当于往x轴投影, 如式(20)所示.

$Vi = \sum\limits_{i = 0}^{\Delta y} {f(i, j)} $

(20)

其中, 当 $f(i, j) > 100$ 时, $f(i, j) = 1$ , 当 $f(i, j) \le100$ 时, $f(i, j) = 0$ , Δy是ROI在y轴方向的长度.

在图12中, 从左往右依次是包含黑色区域, 纯白色区域, 所以生成的Vi数组从左往右必然是谷, 峰, 取峰值处的横坐标x₀为生成的垂直线段L2的起点P3的横坐标, L2的终点P4的横坐标也取x₀, P3, P4纵坐标取ROI沿y轴方向的起点和终点的纵坐标, 连接P3, P4即得到图13中的垂直线段L2.

2.6 计算极差

视频检测时软件连续的采集帧. 对于每一帧, 进行上述的处理, 生成摆轮的水平边缘线和垂直边缘线. 摆轮的平面是否平整反映在数据上就是生成的水平线的位置的偏差大小. 统计同一个零件的一定数量的帧的水平线位置的极差, 依据极差判断出摆轮表面平整度是否合格. 另外, 工厂还需检测摆轮的边缘处弧度是否标准, 这可以通过图13中一定数量帧的垂直线的极差来判断.

3 结果分析

按照机械手表行业的规定, 2 g微型摆轮产品合格的标准是端跳、径跳最大偏差都不大于2丝. 端跳对应图13中垂直边缘, 径跳则对应水平边缘. 系统计量的单位是像素, 摆轮的度量单位是丝.

如图14所示, 获取到摆轮上下边缘直线的纵坐标y1, y2, 经检测 $\Delta y = y2 - y1 = 908{\rm{ - }}814 = 94$ 像素, 已知摆轮设计的厚度为47丝, 所以得到下面的换算关系:

$1{\text{像素}} = 0.5{\text{丝}}$

(21)

这样, 在统计动态极差的时候以不大于4像素作为合格的标准.

为了检测算法的稳定性, 对400个摆轮零件进行了测试, 其中200个合格品, 200个不合格品. 对于每一个零件的检测结果, 都与人工检测结果进行比对. 软件检测结果如表1所示.

经分析, 出错的原因在于ROI位置设置的有些远离摆轮末端, 重新设置至摆轮末端后, 这类误检情况没有再出现.

分析表明, ROI的标记位置是一个影响因素. 正确的标记方法是将此区域标记在摆轮的末端, 如图12所示. 如果标记在远离末端位置, 零件旋转时靠中间的位置其摆动幅度较小导致统计的极差较小, 这样可能会导致误判. 检测系统使用背光源, 所以必须在周围遮光的条件下进行, 如果周围有亮光射入实验台就可能干扰实验结果.

选取有代表性的7个合格品和7个缺陷品, 其测试数据见表2. 表中偏差值的单位是像素.

系统检测实况如图15所示. OK表示合格品, NG表示缺陷品.

系统通过亚像素算法得到的像素点的位置是浮点型数据, 根据式(22)将亚像素位置精确到0.5像素的整数倍.

$ x = \left\{ \begin{array}{l} \left[ x \right],x < \left[ x \right] + 0.5\\ \left[ x \right] + 0.5,x \ge \left[ x \right] + 0.5 \end{array} \right. $

(22)

其中, x表示偏差值, $x \ge 0$ .

表2中, 产品序号为2、6、7的零件径跳最大偏差值都是4像素, 属于合格品. 产品序号为12、13的零件径跳最大偏差为4.5像素, 属于缺陷品. 系统在工厂进行了6个月的试运行, 具有4、4.5这样偏差数据的摆轮普遍存在, 系统检测的结论得到了充分的验证.

由实验中人工和软件检测结论的一致性可以进一步确定, 4像素小于等于2丝, 4.5像素大于2丝.

$ \left\{ \begin{array}{l} 4{\text{像素}} \le 2{\text{丝}} \Rightarrow 0.5{\text{像素}} \le 0.25{\text{丝}}\\ 4.5{\text{像素}} > 2{\text{丝}} \Rightarrow 0.5{\text{像素}} > 0.22{\text{丝}} \end{array} \right. $

(23)

由此可知, 使用0.5像素代表0.25丝的误差小于0.03丝.

在上述算法中, 亚像素位置的计算对于准确度起着重要作用. 项目中偏差值的精确度为0.5像素, 在实验条件下, 对应0.25丝的实际长度, 这一对应关系误差小于0.03丝. 这能够满足工厂对摆轮的检测要求.

4 结语

目前微型零件检测技术逐步向非接触式检测、数字化检测等方向发展^[11], 引入机器视觉检测技术, 既能保证检测的结果更加精确, 可解释, 又能弥补工人数量不足的问题, 深受企业的欢迎. 本文提出一种微型摆轮的机器视觉检测算法, 算法的平均准确率为99.5%, 单帧检测时间平均27 ms, 一个零件可以在2秒钟之内检测出结果. 实验结果表明:该算法能够实时和准确的检测摆轮的表面平整度和边缘整齐情况, 能够满足工业检测的要求.

目前工厂仍在使用人工上料, 如果未来能够使用精密机械成批的上料, 那么整体检测的效率会更高.