聚类分析是数据挖掘研究的一项重要技术, 属于无监督机器学习方法, 其目的是根据已知数据, 计算各观察个体或变量间相似度的统计量, 然后根据某种准则(如最短距离法、最长距离法、中间距离法、重心法), 使得同一类内的相似度最大, 类间相似度最小, 最终将观察个体或变量分为若干类. 常用的聚类分析方法包括基于划分的方法, 基于密度的方法, 基于网格的方法, 基于模型的方法和基于变换的聚类算法. K-means聚类算法的基本思想: 首先, 根据聚类数目k, 选择一定数目初始聚类中心; 然后, 计算某一点到每一聚类中心的距离, 并将该点归入最小的类中; 接着, 基于新的聚类计算新的聚类中心, 并基于新的聚类中心进行新的聚类. 上述过程依次进行, 直到达到最佳的聚类效果.
K-means聚类算法在交通大数据的应用中, 聚类效果明显, 聚类快速且易于实现. 但是K-means算法也存在一定的局限性, 如对“噪声”和孤立感(异常点)敏感, 无法掌握数据分布情况, 人为设定分簇数目, 需要增加迭代次数以取得良好的聚类效果; 算法时间复杂度高, 经常以局部最优结束, 难以达到全局最优. 为解决以上问题, 文献[1]提出基于自适应布谷鸟搜索的K-means聚类改进算法, 试图解决K-means聚类算法受初始类中心影响的问题, 该算法适用于海量数据聚类, 但是集群节点数量对算法的效率具有一定的影响, 算法的稳定性同时有待提高; 文献[2]基于最小化生成树初始化类中心, 有效提高了聚类算法的准确率, 但算法效率有待改进; 文献[3]提出使用cannopy方法对数据预处理从而得到初始聚类中心的方法, 该方法对于交通数据聚类具有一定的复杂性; 文献[4]提出将遗传算法和K-means算法融合, 解决K-means容易陷入局部最优的问题, 但是需要多次进行遗传操作, 具有一定的复杂性. 文献[5]将人工蜂群算法和K-means算法相结合, 克服人工蜂群初始化随机性和K-means算法的敏感性, 加快了收敛速度, 同时, 引入了较高的时间复杂度; 文献[6]将粒子群算法和K-means算法结合, 利用粒子群全局搜索和K-means局部搜索的优势达到最好的聚类结果, 但是算法运行时间还有待优化. 文献[7]通过样本数据分层获取聚类数搜索范围从而获得最佳聚类数; 文献[8] 通过设定AP算法的参数, 基于最大最小距离算法思想设定初始聚类中心和确定聚类数目, 但是参数的设定对聚类效果会有一定的影响. 将K-means算法应用于交通数据聚类中, 文献[9] 用K-means算法分析杭州市通勤特征,杭州市总体达到职住平衡; 文献[10]通过引入Canopy-K-means改进聚类算法,得到客源地的出行热点区域,并将该区域和已有公交站点对比,分析公交站点存在的合理性.
基于不同的思想, 已经有学者提出了多种不同的聚类数选择方法. 在避免局部最优问题中, 提高了聚类准确度, 但聚类效率仍有待提高. 本文通过计算点之间的互信息来寻找聚类中心; 寻找聚类数目时, 基于互信息和散度的比值, 用比值来衡量聚类效果, 从而决定最佳聚类数目. 此方法不需要人为设定聚类数据, 避免了主观设置聚类数目对聚类产生的影响, 提高了聚类效率, 保证了K-means算法聚类结果的有效性和稳定性.
1 本文算法 1.1 相关概念(1) 互信息
互信息[11]是信息论中的一个基本概念, 利用两个随机变量 的联合分布 与乘积分布 的相对熵, 测量两随机变量的相互依赖程度. 将互信息应用在交通数据聚类中, 其互信息可表示为:
| $ I(X;Y) = \sum\limits_{x \in X} {\sum\limits_{y \in Y} p } (x,y)\log \left( {\frac{{p(x,y)}}{{p(x)p(y)}}} \right) $ | (1) |
其中, X为经度, Y纬度, p(x, y)为下车点的经纬度, p(x)为经度出现的概率, p(y)为纬度出现的概率, p(x, y)、p(x)、p(y)可以根据原始交通数据求得, 进而可以求得互信息的值, 参考计算得到的互信息值决定是否将待分类点归入这个类. 通常互信息越小, 两变量间相似度越大, 将互信息较小的点归为一类, 使得类内之间相似性较高, 类内点较紧凑.
1.2 相对熵相对熵[12], 是两个概率分布间差异性度量, 其非负性, 使得相对熵可用于描述两组变量之间的聚类. 传统的样本相似性度量方式如欧氏距离、曼哈顿距离、余弦相似性等难以对不同分布间的相似性进行度量. 相对熵的定义为:
| $ {D_{KL}}\left( {{f_m}(x){g_q}(x)} \right) = \sum\limits_{x \in X} {{f_m}} (x)\log \left( {\frac{{{f_m}(x)}}{{{g_q}(x)}}} \right) $ | (2) |
评判聚类效果优的标准为: 类内的差异尽可能小, 类间差异尽可能大. 聚类数K值发生变化时, 簇类间的差异值以及簇类内的差异值随之变化, 我们把簇类内差异值与簇类间的差异值之比定义为聚类效果优劣程度的评判标准S(式(3)), 簇类内差异值用样本间的互信息I表示, 簇类间的差异值用相对熵表示.
| $ S = \frac{{I(X;Y)}}{{D_{KL}^{}(f_m^{}(x)||g_q^{}(x))}} $ | (3) |
根据评判聚类效果优的标准, 结合交通数据, 当互信息I尽可能小, 相对熵尽可能大时, 聚类效果较好, 在式(3)中, 当S达到最小值, 此时的聚类效果最好.
1.4 算法实现过程实现得到最优聚类数的改进算法的步骤大致如下:
(1)加载样本数据集.
(2)计算样本信息熵, 选择能最大限度降低信息熵的簇划分为两个簇.
(3)确定聚类中心, 选择联合概率 较大的点为聚类中心点.
(4)对现有簇计算S值.
(5)设置判断值H,H=S.
(6)重复步骤(2)(3)(4),若计算的的S<H,说明这一次聚类效果比上一次聚类效果好, 继续迭代; H=S, K+1, 并执行步骤(2)(3)(4), 否则, 停止迭代并返回K.
(7)输出最优聚类数K值下的聚类结果.
2 实验 2.1 实验数据准备为了检测本文提出算法的有效性和可靠性, 本文分别采用滴滴公司盖亚计划(
| 表 1 成都市10月1日8点下车点出租车数据 Table 1 Chengdu taxi point data at 8:00 on October 1 |
2.2 实验结果
将表1中的数据在传统K-means聚类下, 聚类效果如图1所示.

|
图 1 传统K-means聚类结果 Fig. 1 Traditional K-means clustering results |
图4(a)为表1 数据进行数据可视化后的显示图, 四个圆为聚类中心点. 图4(b)为利用表1数据进行热力图可视化的显示图.
传统的K-means算法, 通过手动设置聚类数目K, 聚类效果如图1所示, 其中横坐标表示经度(/°), 纵坐标表示纬度(/°). SK-means算法聚类效果如图3 所示, SK-means算法通过迭代自动寻找聚类数目为4, 通过对比可以看出, 传统的K-means算法需要手动设置聚类数目, 同时, 相同聚类数目时, 聚类效果不够稳定, SK-means自动寻找聚类数目, 多次运行聚类效果较为稳定. DBSCAN算法是基于密度分类, 其对任意形状数据聚类和识别噪声点的优势使其广泛应用于交通大数据中, 其聚类效果如图2所示, DBSCAN算法需要对距离阈值和邻域样本数阈值进行大量联合调参, 由于交通数据的特殊性, 使其聚类过程具有一定的复杂性. 图2中左图聚为4类, 右图聚为3类, 和SK-means算法相比, 类间距离相差较近, 类内距离相差较远, 不能满足较好的聚类条件.
2.3 算法分析表2是传统K-means与本文SK-means算法的性能对比, 通过对比两者的信息熵, SK-means类内信息熵较小、类间信息熵较大, 说明类内下车点更加聚集, 类间下车点较离散. 通过对比minSSE, SK-means具有更小的最小均方误差. SK-means聚类时间相比传统K-means较长, 当考虑到聚类精度, 同时不需手动设置聚类数目时, 所用的时间是可以接受的.
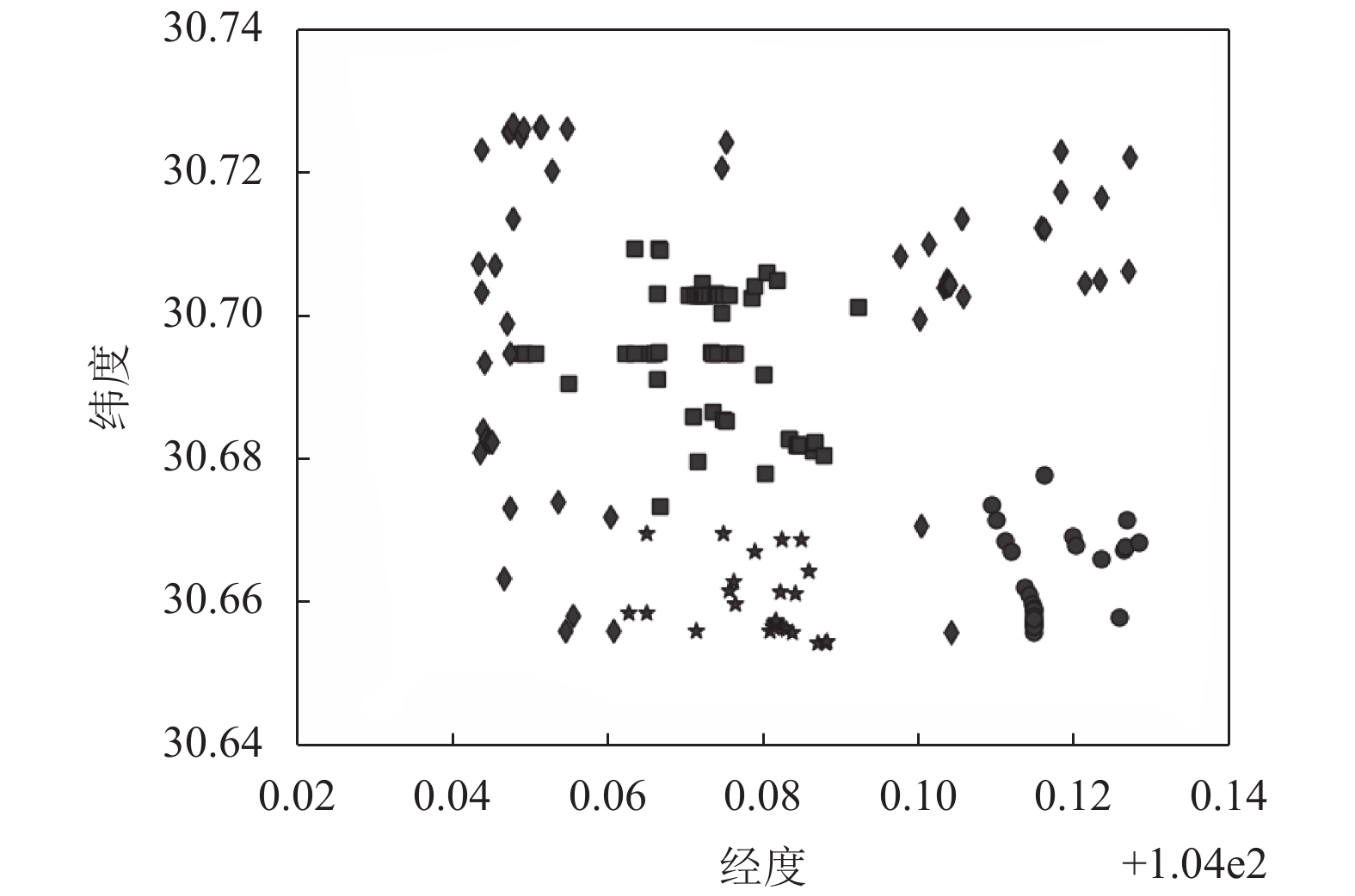
|
图 2 DBSCAN聚类结果 Fig. 2 Traditional K-means clustering results |
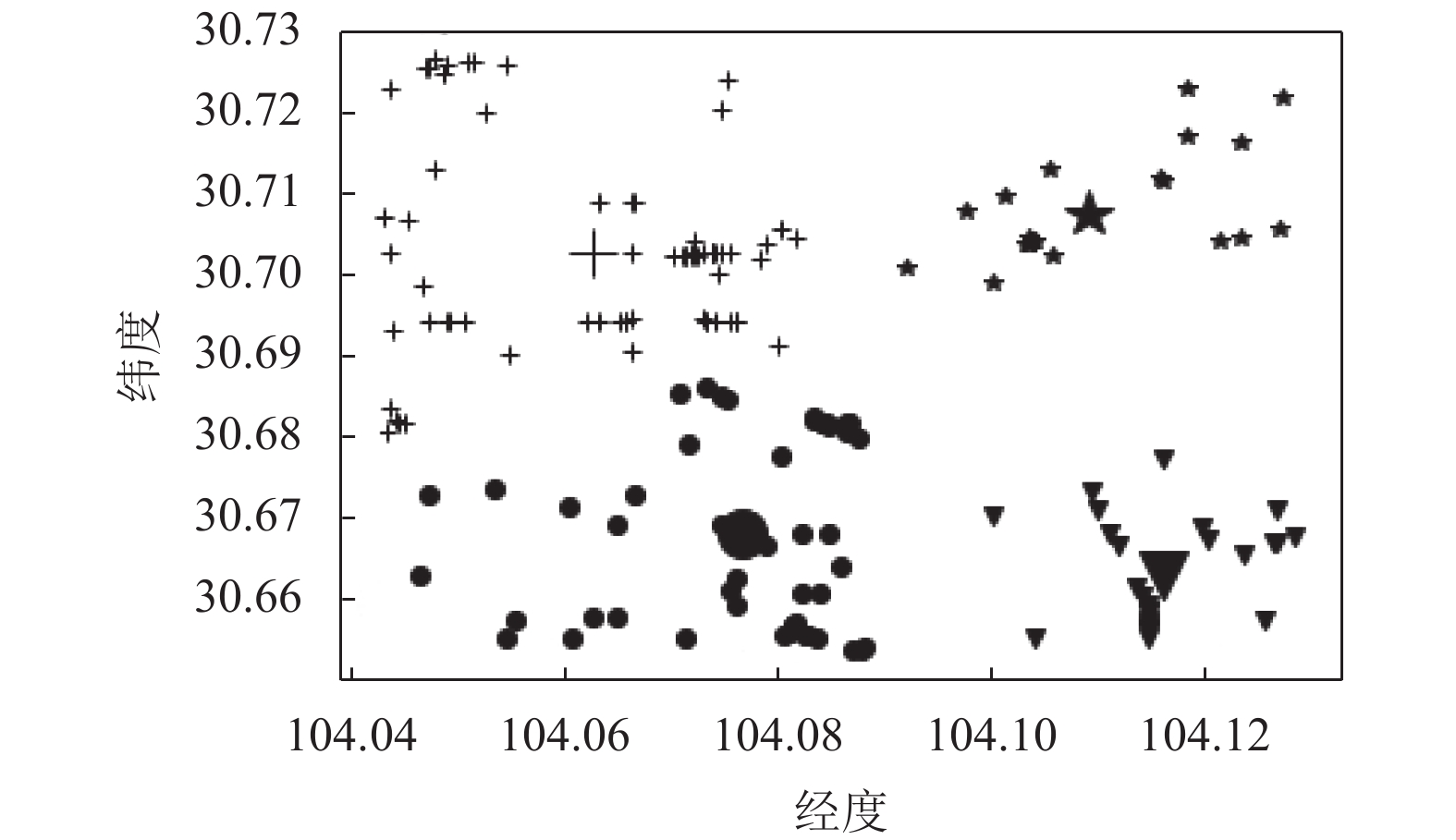
|
图 3 SK-means聚类结果 Fig. 3 SK-means clustering results |

|
图 4 下车点数据图及热力图 Fig. 4 Get off point data map and heat map |
对比SK-means算法和传统K-means算法进行聚类分析后得到的聚类结果, 我们不难发现: 从信息论角度来看, 通过计算两变量的联合概率, 选出其最大的点作为聚类中心, 用互信息衡量类内变量之间的相关性, 互信息越小, 两变量相关性越大, 用相对熵来衡量类间相似性, 相对熵越大, 类间分布差异性越大. 通过互信息和相对熵的比值来决定聚类次数, 当互信息较小, 相对熵较大时, 即比值最小时, 聚类效果最好, 可以有效避免局部收敛. 在改进后的算法中, 我们并没有预先设定聚类数K值, 主要是通过算法本身的循环迭代计算以及判定比较, 最终输出了较好的聚类效果. 与此同时, 在多次运行我们的的改进算法的情况下, 所得到的聚类结果都是一致的, 这也证明了改进算法的稳定性. 由此, 我们可以得到结论, 改进的K-means算法, 具有一定的稳定性和可靠性.
| 表 2 算法性能对比 Table 2 Algorithm performance comparison |
3 结论
交通数据在时空上具有一定的多变性, 利用有效的聚类方法能够更好地揭示潜在的用户行为模式, 传统的K-means聚类由于基于聚类数量, 不能合理解释变化的人流热点. 本文通过基于信息论的方式计算每一次聚类效果, 并将其作为反馈来判断是否继续进行迭代, 从而找到最佳聚类数和最佳聚类中心, 在性能上提高了对空间聚类的判别效率, 其聚类方法还有一定的改进性, 但其聚类精度还需进一步完善.
| [1] |
王波, 余相君. 自适应布谷鸟搜索的并行K-means聚类算法. 计算机应用研究, 2018, 35(3): 675-679. |
| [2] |
李春生, 王耀南. 聚类中心初始化的新方法. 控制理论与应用, 2010, 27(10): 1435-1440. |
| [3] |
Zhang G, Zhang CC, Zhang HY. Improved k-means algorithm based on density canopy. Knowledge-Based Systems, 2018, 145: 289-297. DOI:10.1016/j.knosys.2018.01.031 |
| [4] |
Lu B, Ju FY. An optimized genetic K-means clustering algorithm. Proceedings of 2012 International Conference on Computer Science and Information Processing. Xi’an, China. 2012. 1296–1299.
|
| [5] |
喻金平, 郑杰, 梅宏标. 基于改进人工蜂群算法的K均值聚类算法. 计算机应用, 2014, 34(4): 1065-1069, 1088. |
| [6] |
陶新民, 徐晶, 杨立标, 等. 一种改进的粒子群和K均值混合聚类算法. 电子与信息学报, 2010, 32(1): 92-97. |
| [7] |
王勇, 唐靖, 饶勤菲, 等. 高效率的K-means最佳聚类数确定算法. 计算机应用, 2014, 34(5): 1331-1335. DOI:10.11772/j.issn.1001-9081.2014.05.1331 |
| [8] |
周世兵, 徐振源, 唐旭清. 新的K-均值算法最佳聚类数确定方法
. 计算机工程与应用, 2010, 46(16): 27-31. |
| [9] |
周天绮, 杨志民. 一种改进的K-means算法在城市通勤研究中的应用. 计算机应用与软件, 2019, 36(3): 265-270. DOI:10.3969/j.issn.1000-386x.2019.03.047 |
| [10] |
刘旭, 陈云波, 施昆, 等. 结合Canopy-K-means算法和出租车轨迹数据的公交车站预测方法. 测绘通报, 2018(11): 63-68. |
| [11] |
梁武, 苏燕. 基于改进互信息函数的文本分类方法研究. 科技通报, 2018, 34(11): 188-191, 196. |
| [12] |
姚志均, 刘俊涛, 周瑜, 等. 基于对称KL距离的相似性度量方法. 华中科技大学学报(自然科学版), 2011, 39(11): 1-4, 38. |
 2020, Vol. 29
2020, Vol. 29



