网络层次设计进行网络社区检测的有效方式, 在社交网络、教育社区数据挖掘和犯罪特征识别等领域得到了广泛的应用. 网络层次本质上是由不同尺度上社区内连接密度的异构性定义^[1], 若社区内的连接密度大于社区之间的连接密度, 则网络社区组织结构具有层次性. 将网络划分成若干个连接相对紧密的社区, 每个社区又可能包含若干个连接相对更紧密的子社区^[2–4]. 例如: 存在一个具有40个节点的二层网络组织, 设网络的一个社区C_i内部连接密度为p₁, 它到网络其余部分的密度为p₀, 则有p₁>p₀; 如果社区 C_i由许多小的社区C_ik构成, C_ik的连接密度为p₂, 则有 p₂>p₁. 如何抽取网络层次社区结构是当前的一个重要研究热点^[4].

抽取网络层次社区结构的主要方法是基于层次聚类方法^[5,6], 其思想是采用谱顶层分割的算法将k最近邻图划分成大量较小的子社区, 并用相似的子社区反复地合并操作; 文献[7]利用谱顶层分割的方法, 提出了一种基于马尔可夫链的蒙特卡罗抽样技术预测丢失连接, 用于推导复杂网络的层次, 但由于其算法的抽取的空间较大, 容易导致数据的维度问题; 文献[8]提出了多层次节点相似的网络社区发现方法, 在改进节点相似度和团体连接紧密度的基础上构建社区发现模型, 从而更加准确地找到社区成员, 但这种方法未考虑网络的层次的异构特性, 且不能很好地适用于大型网络; 文献[9,10]提出了多尺度方法揭示不同尺度下的社区结构, 该方法对异构网络的检测具有较好的效果, 但未考虑社区内外连接密度的动态变化和社区间的异构性, 使该方法不能适用于动态演化的网络社区.

基于以上问题, 提出了一种基于谱顶层分割的网络社区层次抽取方法, 该方法将网络的顶层分割定义为某个子网络的二分使得没有任意一个顶层社区横跨两部分, 并给出了顶层分割的期望划分; 引入队列的思想计算社区连接密度, 自顶向下逐层分解给定网络, 提出社区层次抽取算法; 通过实验验证所提出方法的科学性和合理性.

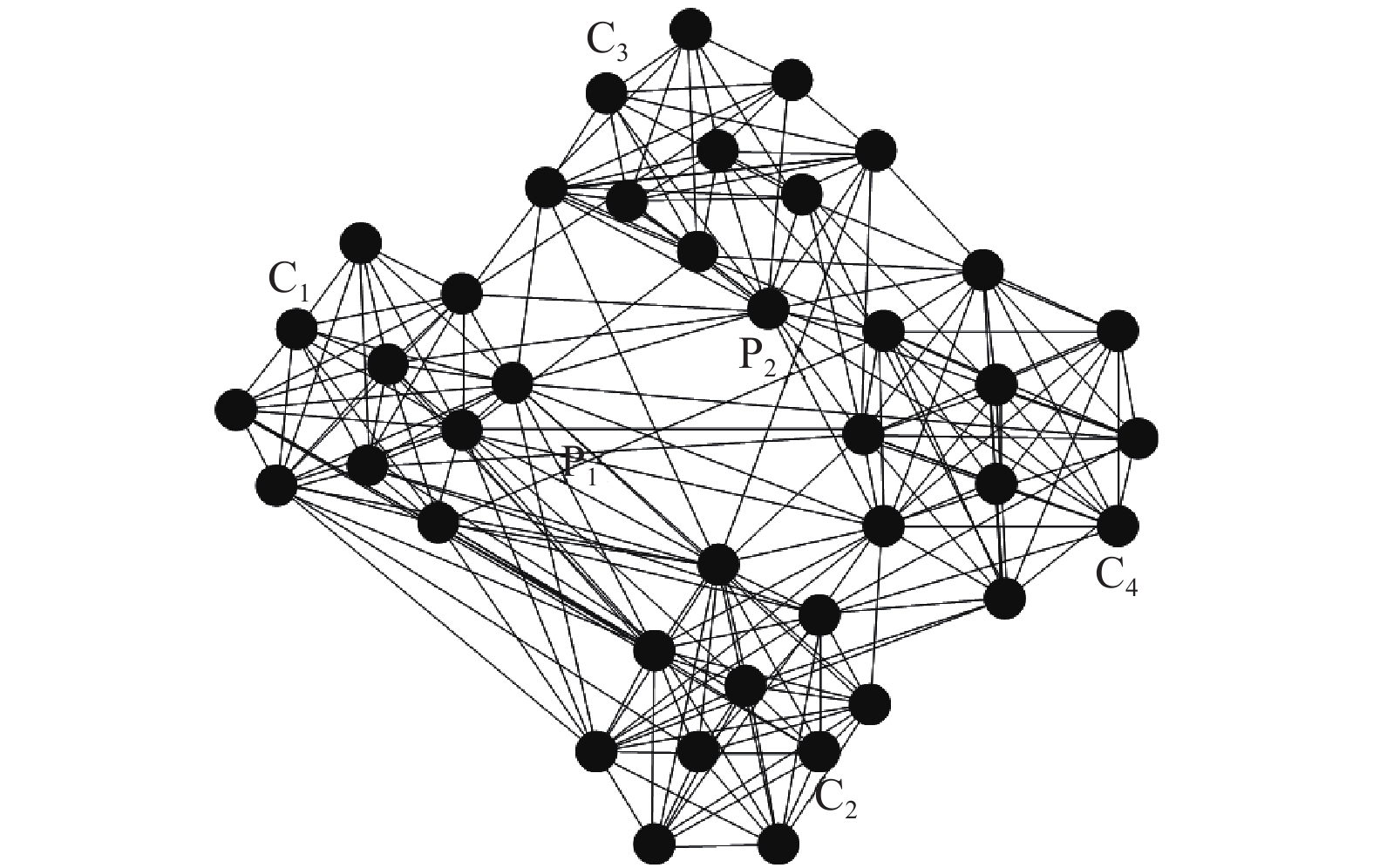
1 谱顶层分割 1.1 顶层分割

存在一个具有内部结构的网络N, 所有构成它的第一层的社区称为关于该网络N的顶层社区, 所有顶层社区的集合称为N的顶层分解, 而使N的顶层分解中所有节点只存在于一个分组中的方法则为N 的谱顶层分割, 进而形成一个网络的二分, 使没有任何一个顶层分解跨越得到两个组. 如图1所示, 在具有两层网络组织结构中, P₁和P₂为网络N的顶层社区, 社区C₁和C₂为P₁的顶层社区, 则P₁-P₂是网络的顶层分割, C₁-C₂是 P₁的顶层分割.

谱顶层分割可以期望找到一个顶层分割或近似顶层分割, 由于每次分裂总是试图找到模块度最大或者增量最大的二分, 如果考虑更多的特征向量, 找到一个顶层分割的机会将进一步增强. 因此, 为使顶层分割得到较高的模块度, 需计算期望最高划分, 从而选择连接密度最小的返回顶层分割.

1.2 谱顶层期望划分

设存在具有3个社区C₁、C₂和C₃的随机网络, 假设连接概率的如表1所示且p₀ < p₁ < p₂.

谱顶层分割设置了一个两层次网络, 即由C₁和C₂构成的社区和C₃形成了网络的第一层, 而C₁和C₂形成了第二层. 对于该网络, 存在3个二分, 即π₁: (C₁, C₂)- (C₃), π₂: (C₁, C₃)- (C₂)和π₃: (C₁) - (C₂, C₃). 为进一步分析, 将3个连接概率参数设置为: p₀=0.1, p_n=p₀+k_n×r_n. 其中, p₀作为社区与社区之间划分的初始连接概率, p_n在p₀的计算基础上设置连接概率, 并以k_n和r_n取值[0, 1]中的随机数, 这里统一取k_n=0.5且r_n=0.5, 以保持网络层次的稳定性, 以免在出现连接状态层次不统一问题. 在给定一个网络N的前提下, 设Q为期望划分值, 对两个层次的期望则定义为:

$\begin{gathered} Q\left( {{p_1}} \right) = {m_1} \times {m_2} \times {p_0} - \frac{{{{\left( {{k_1} + {k_2}} \right)}^2} + k_3^2}}{{2M}} \\ Q\left( {{p_2}} \right) = {m_1} \times {m_3} \times {p_1} - \frac{{{{\left( {{k_1} + {k_3}} \right)}^2} + k_2^2}}{{2M}} \\ Q\left( {{p_2}} \right) = {m_1} \times {m_3} \times {p_1} - \frac{{{{\left( {{k_1} + {k_3}} \right)}^2} + k_2^2}}{{2M}} \\ \end{gathered} $

(1)

式(1)中,m_i和k_i分别是社区i的尺寸和总度. 通过计算期望划分值可以将连接密度最小社区作为顶层分割, 进而对网络层次进行抽取.

2 网络层次社区抽取 2.1 连接密度计算

为获取连接密度最小的社区, 引入队列思想对网络N自顶向下逐层分解, 采用q_curr 表示存储网络第h层的有待分析社区, q_work表示当前工作队列, q_next表示存储下一层社区. 当初始化时, q_curr存储包含网络中所有节点的唯一组, 从q_curr的队头中取出第一组并将其存入网络N, 然后将其分解成两组网络数据N₁和N₂, 并计算其连接密度:

$\delta _{\rm{0}}^{\rm{*}} = \frac{{\left| {E\left( {\rm {N_1},{N_2}} \right)} \right|}}{{\left| {\rm {N_1}} \right| \times \left| {\rm {N_2}} \right|}}$

(2)

式(2)中, E(N₁, N₂)表示网络N₁和N₂之间的边数, 而计算连接密度是关于N的顶层社区间的连接密度的一个估计.

当N₁和N₂进入工作队列q_work时, 都可能包含几个谱顶层分割. 如果当前q_work非空, 则可以从中取出第一组网络数据N₁并对它进行分解; 如果不可分, 则N₁被认为是一个顶层社区, 否则它被划分为两个更小的组N₁₁和N₁₂, 并实时检查它们之间的连接密度 ${\delta _{\rm{1}}}$ , 计算是否超过谱顶层分割间连接密度的估计值 $\delta _{\rm{0}}^{\rm{*}}$ . 如果计算结果大于估计值 $\delta _{\rm{0}}^{\rm{*}}$ , 则此分割不属于h层分解, 而属于h+1层分解. 由此推知, N₁是关于网络N的一个谱顶层分割, 则N₁进入q_next准备下一层分解, 否则, N₁₁ 和N₁₂都可能是一个谱顶层分割或者几个谱顶层分割. 因此, 为进一步取代N₁, 需进入q_work调整估计值 $\delta _{0}^{*}$ , 调整估计值方法的思路是将原有的估计值在顶层分割次数的基础上对下一层网络分割后连接密度的预判, 可以实时检测顶层分割后的每一层网络的连接概况, 从而提高下一层分割的精准性. 其计算方法如下:

$\delta _{0}^{*} = \frac{{\delta _{0}^{*} \times n + {\delta _{1}}}}{n + 1}$

(3)

式(3)中, n表示网络N从q_curr中取出后, 执行顶层分割的次数, $\delta _{\rm{0}}^{\rm{*}}$ 表示新的值. 当q_work为空时, 表示从q_curr中取出的第一个组N₁已经完全分解为它的顶层社区; 而从q_curr中取出下一个组直到q_curr为空, 将q_next中的组移到q_curr, 并进行h+1层分析, 重复上述过程得到调整后的估计值.

2.2 算法实现

抽取网络层次由算法1实现, 在该算法中函数subspaceMethod (G, N₁, N₂, ${\delta _{\rm{1}}}$ , d)为搜索一个顶层分割, 将N分解为两个组N₁和G₂, ${\delta _{\rm{1}}}$ 为两部分间的连接密度, d指示了N是来自于q_curr(d=0)还是来自于q_work (d>0). 符号“←”和“→”对应队列的两个基本操作, 即“从队头取元素”和“存储数据到队尾”, 而q_a $\Rightarrow $ q_b表示将队列q_a的所有数据移到另一个队列q_b, 算法实现如算法1.

算法1. 层次抽取算法(伪代码)

输入: q_curr, q_work, q_next

输出: 新的层次社区

1) initialize q_curr, q_work, q_next

2) N→q_curr, h=0 //N表示整个网络

3) while q_curr is not empty do

4) 　while q_curr is not empty do

5) 　　N←q_curr,d=0

6) 　　　 v=subspaceMethod (N, N₁, N₂, δ₁, d)

7) 　　　if v>0 then //N未被分解

8) 　　　　N₁→q_work, N₂→q_work, δ^*=δ₁

9) 　　　end if

10) 　　　while q_work is not empty do

11) N←q_work and v=subspaceMethod (N, N₁, N₂, δ₁, d)

12) 　　　　if v<=0 then N→q_next

13) 　　　　else if $\scriptstyle{\delta ^*} < = \beta \times {\delta ^*}$ //β确定一个划分是否属于下一个层次

14) 　　　　N₁→q_work, N₂→q_work update δ^*

15) 　　　　 d=d+1, compute(Q)//计算期望划分值

16) 　　　　else N→q_next //N为最顶层社区

17) 　　　　end if

18) 　　　end if

19) 　　end while

20) 　　end while

21) 　 h=h+1

22) 　if q_next is not empty then output the communities at h level from qnext //返回新的层次社区

23) 　 q_next $\Rightarrow $ q_curr

24) 　end if

25) 　end while

由于对网络分割的顺序取决于集合之间边的密度, 因此上述算法可看作为一种有序的谱方法, 首先搜索一个顶层分解并计算网络的特征向量, 判断网络N是否被分解状态, 然后进入队列进行顶层分割; 在 ${\delta ^*} \Leftarrow $ $\;\beta \times {\delta ^*}$ 中, 参数β的选择确定一个划分是否属于下一层次, 本文设置β=1.6, 为实验测试设定一个稳定值, 以解决该值太小导致连接密度的同质性较高以及异质性较强的问题.

3 实验分析

仿真实验在gephi软件平台上验证本文方法的有效性, 数据来源于Rovirai Virgili^[11]大学Email数据中的教师联系网络, 该网络由7个主要学院的教师共640个节点构成的三层次网络, 自顶向下分别为学院、系和研究组, 网络第一层由4个160节点的社区构成, 每个类似的社区在第二层分解为4个40节点的小社区构成, 而每个小社区又在第三层包含了4个10节点的更小社区, 网络的边按照各层的不同的连接密度生成的, 满足p₀<p₁<p₂<p₃, 实验中设定p₀=0.005, p₁=0.2, p₂=0.4, p₃=0.8. 通过比较同步法和多尺度法^[12]测试层次随机网络, 同时在Email现实网络上测试本文方法的性能.

3.1 同质层次随机网络性能

对于数据源中学院、系、研究组, 其每个层次具有相似的层次分布结构, 在满足所有层次比例µ= k<h/k_l^[13] 的情形下, 它表示了层次的相对凝聚性, 若µ越小, 则凝聚性越强, 反之则越弱. 为说明本文方法的鲁棒性, 通过调整µ得到不同凝聚强度进行测试, 并采用规范化互信息^[14]度量被划分的分割和已知的分割, 取0≤µ≤1表示无关匹配到完全匹配的状态. 如图2所示, 本文方法可以精确地识别3个层次上的社区, 其规范化互信息的匹配程度均在90%以上.

由图2可知, 对于具有3个同质层的随机网络上的性能, 每一个点是在10个实例网络上的平均, 一个稳定的分割可能对应于某一层次的划分.

由图3可知, 通过本文方法与多尺度法和同步法进行比较, 说明了多尺度法和同步法对3个层次分割的精度. 在最强凝聚情形0.785 和0.885下, 虽然同步法在3个层次上都具有相当高的精度, 但它的精度随着凝聚强度的下降而快速下降; 多尺度法在精度和稳定性方面则更接近本文方法, 但其规范化互信息仍然低于本文方法且不适应于动态演化的网络.

3.2 异质层次随机网络性能

由于在更小的网络社区中, 其每一层所具有的社区的尺寸是完全不同的, 因此需要在通过本文方法验证是否适用于尺寸异质的情形. 由图4可知, 通过实验, 本文方法能够精确地抽取它的层次组织, 其中粗线表示第一层划分, 细线表示第二层划分, 在第二层中社区内的不同灰度节点表示第三层的网络组织, 可以显示层次抽取后的结果.

由图5可知, 谱顶层划分与真实的划分完全一致, 第二层和第三层精确地逼近真实的划分, 按照互信息精度分别为0.93和0.81. 同时, 将本文方法与同步法和多尺度法做了比较, 在第一层社区网络上, 本文方法比同步法和多尺度法在规范化互信息性能上分别高0.05和0.15, 计算精度损失较小, 这是由于在第一层社区网络计算连接密度的数据量较大, 而第二层次和第三层次社区网络上, 本文方法比同步法和多尺度法在规范化互信息性能上的差距逐渐减少, 这是由于本文方法引入了队列的思想, 在空间不足的情形下通过不断调整连接密度的估计值, 实时预判和分析下一层分割网络社区的密度, 在期望划分的驱动下释放密度最小社区的相关节点, 然后再计算连接密度的估计值, 以此类推, 得出最小社区.

4 结论与展望

针对网络的层次社区检测问题, 提出了一种基于谱顶层分割的网络社区层次抽取方法, 选取在线真实数据源作为实验数据, 说明了该方法的科学性和合理性, 为院校社区教育和大数据行为特征识别提供了相关技术基础支持, 下一步将从大数据的角度对社区的层次进行抽取, 利用语义特征检测的方法和大数据优化相关算法, 对社区层次检测的语义性进行探索研究, 以得出更好的实验效果.