智能交通监控系统(ITS)是现代交通体系中不可或缺的一部分[1,2], 智能交通监控系统伴随着图像视频处理、模式识别和机器视觉等多种技术的发展, 已经越来越广泛的应用到城市道路[3]、高速公路[4]、桥梁[5]和隧道[6]等不同场景道路下, 其广泛的应有除了与技术本身发展有关外, 还与不断降低的监控相机与处理器成本、丰富的数据收集有着密切的关系. 目前, 大多数基于视频的研究还仅限于单场景下[7,8], 但是由于单相机场景视野小等因素的影响难以实现对整个交通场景进行智能监控应用, 本文借助单场景下的相机标定以及场景中相机的几何关系来实现多场景的综合相机标定, 并结合多场景综合相机标定来实现交通场景道路拼接, 从而为以后跨相机的广泛应用奠定基础.
相机标定是一个重要的研究领域, 通过相机标定可以实现基于视频的车辆尺寸测量[9]、车辆速度监测[10]和车辆空间位置定位等交通参数信息的获取. 确立相机标定能够构建出图像平面与真实物理世界之间的映射关系[11], 该映射关系的确立来源于简单的相机针孔模型并被定义为相机内参数矩阵和相机外参数矩阵. 相机内参数矩阵表示了相机内部固有的参数, 例如焦距、主点和纵横比等, 而相机外参数表示相机所在坐标系与真实世界坐标系所建立的位置关系参数. 近年来, 科研工作者提出许多交通场景下的相机标定方法, 如严红平等人[12]依据道路标识信息提出基于3个消失点的道路云台相机标定方法. Sochor等人[13]基于车辆3D模型提出交通场景的相机标定方法, 并依据该方法实现车辆速度测量.
场景拼接[14,15]是将带有重叠区域的数张图像或相机场景拼接成一幅完整图像, 其中数张重贴图像或场景可以是同一相机的不同角度拍摄, 也可以是不同相机的相同或不同角度所拍摄, 其中研究较为广泛的是同一相机的不同角度拍摄的场景拼接, 如马嘉林等人[16]通过棋盘标定实现两幅图像的拼接. 但本文所研究是不同相机的不同角度拍摄的道路场景拼接, 其场景拼接是建立在相机标定基础上, 依据逆投影思想和平移矢量关系来实现的.
本文针对单相机由于视野和分辨率有限, 无法对完整道路实现监控与应用, 因此通过基于相机标定的场景拼接方法能够有效的实现全场景覆盖. 首先采用基于消失点的相机标定方法分别对不同相机场景进行标定, 并建立其子世界坐标系关系, 之后依据公共区域特征, 求解两个相机场景对应子世界坐标系之间的旋转平移关系, 最后结合逆投影思想和平移矢量关系, 将不同相机下的子世界坐标系统一到以第一相机为基准的世界坐标系中, 将场景道路信息融入到世界坐标系, 生成完整道路全景拼接俯视图.
1 单场景相机标定 1.1 相机标定相机标定是通过计算相机的内部参数和外部参数来实现的, 本质上是为了构建图像上的像素信息和世界坐标系中物理信息的几何映射关系. 其中内部参数主要包含焦距、主点、纵横比和畸变参数等, 表示图像坐标系上像素信息与相机坐标系中的物理信息的投影变换, 外部参数主要包含旋转矩阵和平移向量, 表示相机坐标系和世界坐标系之间的位置关系[17]. 整个过程(假设世界坐标中的一个点P(x, y, z)到像素坐标系中的一个点p(u, v)的映射)可以通过式(1)表示:
| $ \alpha p = HP{\rm{ = }}KRTP $ | (1) |
其中, K表示相机内部参数, R表示旋转矩阵, T表示平移向量, α为比例因子. KRT可通过H3×4进行表示, 这里H3×4称映射矩阵.
1.2 道路场景标定模型道路场景中的监控相机满足小孔成像模型且其具有自旋角为零、主点位于图像中心等特点. 通常情况下, 监控相机架设在道路旁的支柱上, 该类支柱等距离等高度分布. 依据监控相机自身属性和架设特点, 建立出合理简化的单场景下相机标定模型, 如图1所示, 将世界坐标系原点设置在相机正下方的路面上. YcoZc平面与YwoZw平面均处于平面Ω内, 且平面Ω与道路方向成夹角为θ, Xc轴与Xw轴相互平行且方向一致.

|
图 1 单场景下相机标定模型 |
根据单场景下的相机标定模型, 内参数矩阵为:
| $ K = \left[ {\begin{array}{*{20}{c}} f&0&{{C_x}}\\ 0&f&{{C_y}}\\ 0&0&1 \end{array}} \right] $ | (2) |
其中, f为相机焦距, 其单位为像素, (Cx,Cy)为主点位置是已知参数, 矩阵表示如式(2)所示.
| $ R = {R_x} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos (\phi + \pi /2)}&{ - \sin (\phi + \pi /2)}\\ 0&{ - \sin (\phi + \pi /2)}&{\cos (\phi + \pi /2)} \end{array}} \right] $ | (3) |
旋转矩阵R是世界坐标系绕X轴逆时针旋转ϕ+π/2, 如式(3)所示. 因道路上安装监控相机高度h有统一标准, 因此平移向量T定义为原点沿着世界坐标系的Z轴移动h距离至相机原点, 可表示为式(4).
| $ T = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ { - h} \end{array}} \right] $ | (4) |
因此,
| $ u = \frac{{su}}{s} = \frac{{{X_w}{H_{11}} + {Y_w}{H_{12}}}}{{{X_w}{H_{31}} + {Y_w}{H_{32}} + {H_{34}}}} $ | (5) |
| $ v = \frac{{sv}}{s} = \frac{{ - {X_w}{H_{12}} + {Y_w}{H_{22}} + {H_{24}}}}{{{X_w}{H_{31}} + {Y_w}{H_{32}} + {H_{34}}}} $ | (6) |
在消失点标定原理中, 两个正交方向的消失点可以实现相机焦距和旋转参数的标定, 相机标定模型中选择Y轴方向的消失点vp0(u0, v0)在世界坐标系中无穷远处, 用齐次坐标表示为[0, 1, 0, 0], X轴方向的消失点vp1(u1, v1), 用齐次坐标表示为[1, 0, 0, 0], 将这两个点代入式(5)、式(6)可得:
| $ f = \sqrt { - (v_0^2 + {u_0}{u_1})} $ | (7) |
| $ \phi = \arctan ({{ - {v_0}} / f}) $ | (8) |
| $ \theta = \sqrt {{{({f^2} + v_0^2)} / {({f^2} + u_0^2 + v_0^2)}}} $ | (9) |
从式(7)可以看出f的确定与消失点vp0(u0, v0)和消失点vp1(u1, v1)有关, 如果f可以通过其他方式确定, 则可避免求解垂直道路方向的消失点vp1(u1, v1), 只需要通过计算俯仰角ϕ、扫视角θ和相机高度h, 就可以实现单场景下的相机标定. ϕ与θ可以通过式(8), 式(9)获得, h为已知信息. 接下来则重点说明f的计算过程.
沿道路方向消失点可以通过对道路上实线进行检测, 从而获得第一个方向消失点vp0(u0, v0), 如图2所示, 但是垂直道路方向因不存在标志线, 难以获取该方向消失点, 因而采用沿道路方向一段实际物理标志线长度l来解决该方向消失点难以提取的情况. 如图3所示, 实线长度l可以选择道路上一段虚线或其它线段长短, 将线段前段点(·, yf, 0)投影到图像上的坐标是(·, yf), 同时将线段后端点(·, yb, 0)投影到图像上的坐标为(·, yb), 其中yf、yb之间满足yb=yf+lcosθ, 之后通过将该式及线段上的两组点代入式(5)和式(6)可以得出如下关系式:
| $ \cos \theta = \frac{{fl({v_f} - {v_0})({v_b} - {v_0})}}{{h({f^2} + v_0^2)({v_f} - {v_b})}} $ | (10) |

|
图 2 沿车道方向消失点的确定 |

|
图 3 世界坐标系中的线段示意图 |
通过式(8)和式(9)得出:
| $ {\cos ^2}\theta = \frac{{\left( {{f^2} + v_0^2} \right)}}{{{f^2} + u_0^2 + v_0^2}} $ | (11) |
将式(10)代入式(11)可得式(12), 通过解该方程即可求解出焦距值f, 并依据场景信息匹配排除错误焦距值. 通过道路方向消失点vp0、道路线段长度l和相机高度h即可完成单场景下的相机标定.
| $ {f^4} + [u_0^2 + 2v_0^2 - {\left( {{{wl} / h}} \right)^2}]{f^2} + (u_0^2 + v_0^2)v_0^2 = 0 $ | (12) |
本章节的目的是依据不同相机下提取的相同特征信息来寻求最佳匹配关系, 为完成场景道路拼接奠定基础. 待拼接的图像或待拼接图像的子世界坐标系之间存在旋转、平移在内的多种变换关系, 该部分就是求解待拼接图像的子世界坐标系之间的变换关系.
在交通监控场景下, 针对同一空间位置点在相机视野1中处于较近和清晰位置, 在相机视野2中处于较远和模糊位置, 通过特征点匹配无法实现位置匹配, 本文设计在两个重叠视野里放置不少于4个圆形标志点(假设两个相机视野之间存在少量重叠区域), 人工选取标志点中心, 通过单场景相机标定获取其在相机1所在子世界坐标系坐标P1i (x1i, y1i, z1i), 该子坐标系称作参考坐标系, 参考坐标系表示其他子世界坐标系经过旋转平移的映射变换可以变换到该参考坐标系上. 相机2中标志点中心在子世界坐标系坐标为P2i (x2i, y2i, z2i), 该坐标系称作非参考坐标系, 因此参考坐标系和非参考坐标系之间可用式(13)表示:
| $ \left[ {\begin{array}{*{20}{c}} {{x_{1i}}}\\ {{y_{1i}}}\\ {{z_{1i}}} \end{array}} \right] = M\left[ {\begin{array}{*{20}{c}} {{x_{2i}}}\\ {{y_{2i}}}\\ {{z_{2i}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} r&t\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_{2i}}}\\ {{y_{2i}}}\\ {{z_{2i}}} \end{array}} \right] $ | (13) |
其中, M表示4×4的投影变换矩阵, r是3×3的旋转矩阵, 表示非参考坐标系经过旋转矩阵r可以与参考系坐标系X轴、Y轴和Z轴方向保持一致. t是3×1的平移矩阵, 表示非参考坐标系原点经过平移矩阵可以与参考坐标系原点重合. 通过上面的变换关系式(13),将n组坐标点代入, 之后通过最小二乘法可以求解出该投影变换矩阵M. 到此该部分建立起了两个子世界坐标系之间的映射关系, 结合单场景的相机标定, 构建出多相机视野和同一个世界坐标系的一一对应关系, 其中统一世界坐标系的原点与参考坐标系的原点相同.
2.2 带有真实物理信息的场景拼接在交通监控场景中, 监控相机架设在道路旁, 相机视野覆盖监控道路, 如图4(a), 由于存在透视变换, 导致道路在视野中呈现出近处场景道路宽远处场景道路窄的变化, 显然通过现有拼接技术难以直接对不同相机所在道路进行拼接, 因此本文通过逆投影思想对道路进行含有物理信息的场景道路拼接, 拼接模拟示意图如图4(b)所示, 将场景以俯视图的方式计算在在一个坐标系中, 其中俯视图中任何位置可表示真实场景物理信息.

|
图 4 道路场景拼接模拟示意图 |
在2.1节中我们建立起了不同相机视野和统一世界坐标系的一一对应关系, 也就是说不同相机视野中的点在统一的世界坐标系中能够找到对应的点, 这样能将图像信息变换到世界坐标系中, 从而结合逆投影思想和平移矢量完成带有物理信息的道路场景拼接. 逆投影思想方法具体流程如下.
Step 1. 构建一个容纳两个场景的世界坐标系W1, 从世界坐标系W1原点开始向X轴、Y轴方向以cm级步阶获取世界坐标点(因对道路场景拼接因而始终世界坐标系Z=0), 记为(xi, yi, 0).
Step 2. 因统一世界坐标系与参考坐标系原点、方向一致, 所以两个坐标系之间变换矩阵为单位矩阵E, 因此将该世界坐标点(xi, yi, 0)通过相机标定, 结合式(14)计算出其在相机视野1(参考坐标系所在视野)的位置(ui, vi), 获取相机视野(ui, vi)的像素值, 将该像素值放入统一世界坐标系W2的(xi,yi,0)位置, 整个过程如图5, 依次经过该过程, 直到相机视野1中的道路信息全部放入世界坐标系W2中.
| $ \left[ {\begin{array}{*{20}{c}} {{u_i}}\\ {{v_i}}\\ 1 \end{array}} \right] = {K_1}{R_1}{T_1}E\left[ {\begin{array}{*{20}{c}} {{x_i}}\\ {{y_i}}\\ 0\\ 1 \end{array}} \right] $ | (14) |
Step 3. 对于相机视野2, 因统一世界坐标系与非参考坐标系存在位置和方向上的差别, 因此通过2.1节中所求得的透视变换M, 同样将世界坐标点(xi, yi, 0)通过相机标定, 结合式(15)计算出其在相机视野2(非参考坐标系所在视野)的位置(ui, vi), 获取相机视野(ui, vi)的像素值, 将该像素值放入统一世界坐标系W2的(xi, yi, 0)位置, 对于部分世界坐标系中的位置不在相机视野范围内可将像素信息记为0.
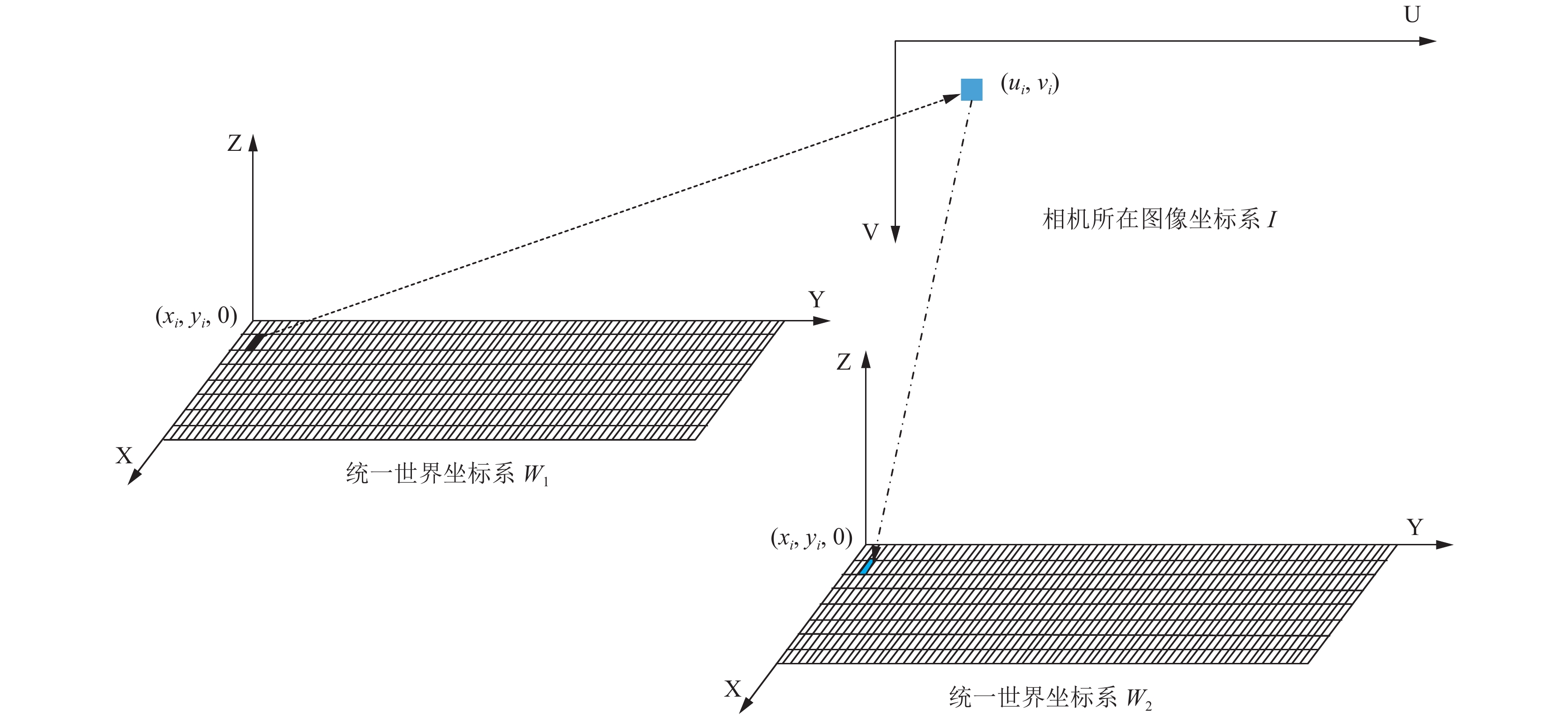
|
图 5 像素信息获取示意图 |
| $ \left[ {\begin{array}{*{20}{c}} {{u_i}}\\ {{v_i}}\\ 1 \end{array}} \right] = {K_2}{R_2}{T_2}M\left[ {\begin{array}{*{20}{c}} {{x_i}}\\ {{y_i}}\\ 0\\ 1 \end{array}} \right] $ | (15) |
到此为止如果对于相机视野2整体采用世界坐标系到图像(获取像素信息)再到世界坐标系的思想完成道路场景拼接是不准确的, 这样对相机视野2远处视野是存在巨大误差的, 拼接结果也是大打折扣. 误差体现在求解两个子世界坐标系之间的旋转平移矩阵M时, 依据的是重叠区域中公共特征, 这是一种局部最优的解决方式, 也就是说在相机2中公共特征处透视变换M是非常准确的, 但是公共特征只存在视野下方(近处), 那么对于上方(视野远处)通过透视变换M误差就会产生, 并且会伴随视野变远误差会越来越大. 针对上述误差, 提出一种平移矢量思想:
Step 1. 求取相机场景2中多个圆标志物中心点在该子世界坐标系下的坐标, 记为(X2i, Y2i, 0), 并通过式(16)和式(17)求解多个标志物的中心坐标为
Step 2. 通过透视变换M求取
Step 3. 如此在统一世界坐标系W1对相机场景2远处进行拼接时, 可对W1中(xi, yi, 0)进行矢量偏移计算得
| $ \overline {{X_2}} = \frac{{\displaystyle \sum\limits_{i = 1}^n {{X_{2i}}} }}{n} $ | (16) |
| $ \overline {{Y_2}} = \frac{{\displaystyle \sum\limits_{i = 1}^n {{Y_{_{2i}}}} }}{n} $ | (17) |
最终能够将两个相机的道路信息都准确无误的放入到统一世界坐标系W2中, 完成含有物理信息的道路场景拼接, 该物理信息是图像上的像素点在空间位置的映射即跨区域的相机标定.
对于在场景拼接的边界处常会出现因像素信息突然过渡而出现明显的拼接缝, 可采用图像融合技术进行处理, 常用的方法有加权平均法、多尺度变换法和多分辨分析等方法. 本文采用加权平均算法处理拼接缝问题, 对拼接重叠区域中像素信息值F由相机视野1对应点像素信息值F1与相机视野2对应点像素信息值F2进行加权平均, 即
本文提出的方法本质上是通过对两个监控场景的标定和投影变换来实现跨相机的标定和道路场景拼接. 为了评价本文提出的方法的可靠性和有效性, 在实际监控场景中进行实验测试, 选择道路中存在重叠区域的两个监控相机并对其图像信息进行采集, 系统的数据测试选在Windows 10系统的Visual Studio 2015开发平台上. 实验分为两个环节, 在3.1对单相机的标定做了误差分析, 在章节3.2对双相机的距离标定和拼接结果做了评价.
3.1 单相机标定误差分析针对监控场景1和监控场景2, 如图6所示, 分别对这两个场景进行单相机标定, 因两个场景标定方法相同,现以监控场景1为例进行说明, 通过章节1可知, 要完成单场景的相机标定, 需要知道沿道路方向消失点vp0(u0, v0), 相机高度h和道路方向一段实际物理标志线长度l, 因此对监控场景1相机高度进行测量, 获得其相机高度h为6.18 m, 同时选取沿道路方向上黄色标志实线l, 根据中国交通部发布的《公路工程技术标准》, 可以了解到二级及以下公路虚线长度满足“长2空4”, 即黄色实线部分长2米, 空白部分长4米, 因此该黄色标志线长度应该为2米, 为保证实验精度, 笔者也对其进行测量, 实际长度为2.05米, 对该场景下道路方向消失点vp0(u0, v0)采用图2消失点确定过程进行确定, 之后结合1.2节算法思想对该场景进行标定.

|
图 6 不同相机监控场景示意图 |
为验证对该单场景标定的准确性, 本文通过标定方式对场景中的线段标志和道路宽度总计12条线段进行计算. 并与场景中实际线段标志和道路宽度尺寸做对比, 其中表1为相机1场景标定结果与真实尺寸的数据对比, 表2为相机2场景标定结果与真实尺寸的数据对比, 数据误差w为对应线段标定值
| 表 1 场景1下线段标定与测量值对比及分析 |
| 表 2 场景2下线段标定与测量值对比及分析 |
3.2 场景拼接误差分析
对图6中两个相机单场景相机标定的基础上, 结合2.1节的子世界坐标系之间投影变化的求解和2.2节带有真实物理信息的场景拼接, 完成了整个多相机视野的道路拼接工作. 本文道路场景拼接通过遍历思想完成统一世界坐标系中每一个点与图像道路像素信息的匹配, 从而构建出带有道路信息的世界坐标系, 试验中完成了相机场景1与相机场景2的道路拼接, 其拼接结果如图7所示.

|
图 7 两个场景下的道路场景拼接 |
本文多场景下的拼接是含有道路物理信息的特殊拼接, 物理信息是指拼接出的全景示意图所有像素的所在位置带有真实物理尺寸信息, 即拼接图中任意两点之间的像素距离就是实际距离, 单位为厘米. 在全景示意图中选了5段距离, 如图8所示, 通过人工实际测量值和系统处理结果做对比, 对比结果如图9所示. 通过图表发现该方法能够较好的实现跨区域道路测量, 为实际应用奠定了良好基础.

|
图 8 全景图中线段选取 |
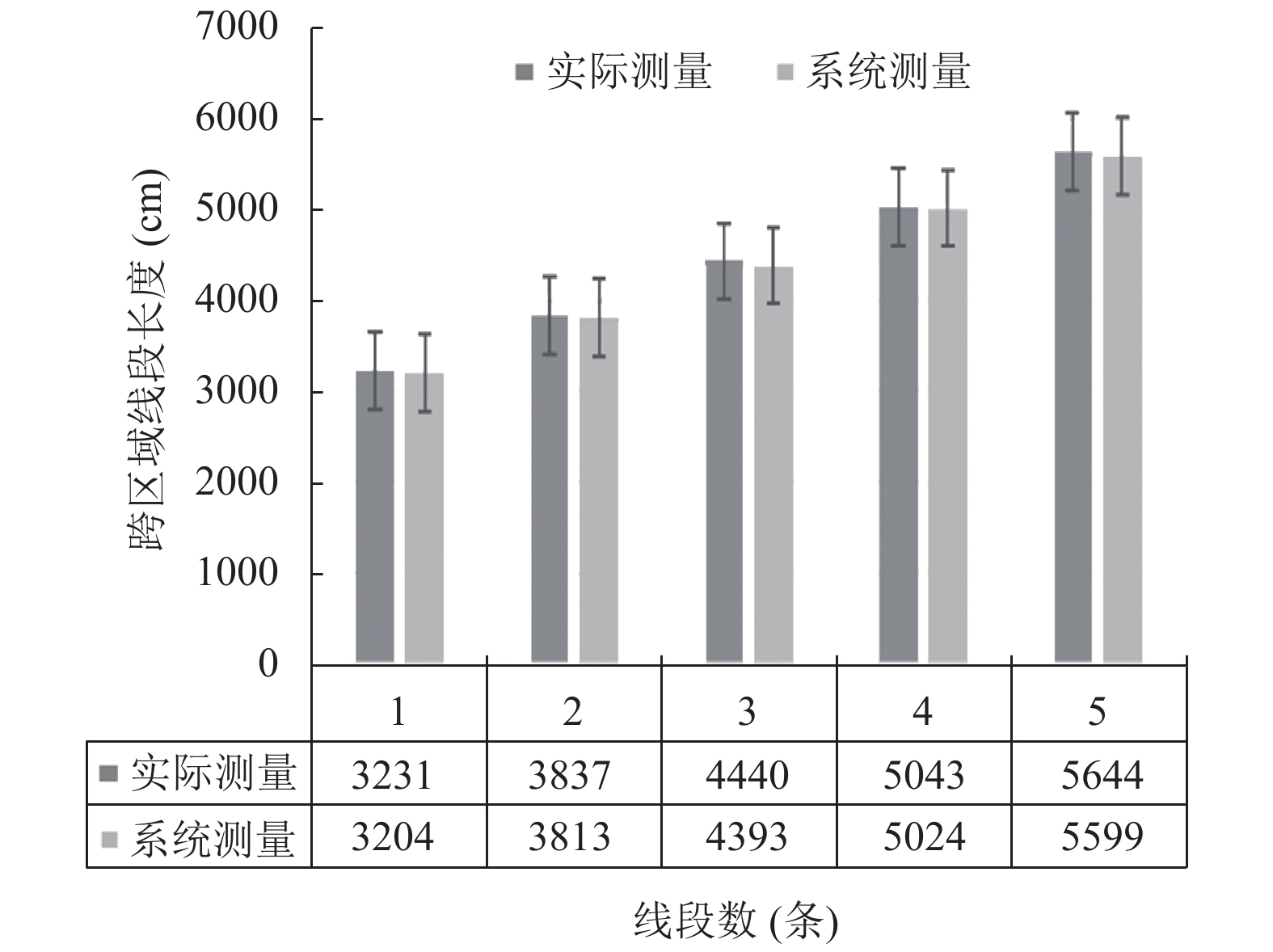
|
图 9 跨区域线段测量与对比 |
4 结束语
本文介绍了一种基于相机标定的跨相机场景拼接方法, 该方法结合单相机标定和空间透视变换完成多相机标定工作, 从而进一步结合逆投影思想和平移矢量思想实现了含有物理信息的道路场景拼接. 实验结果表明, 该方法能够较好的实现道路场景拼接和跨区域道路物理测量, 从而为今后更多实际应用和理论研究奠定基础. 在未来研究工作中, 一方面本文主要针对两个相机进行场景道路拼接, 往后可通过3个相机或更多相机来实现直道甚至弯道的拼接工作, 另外一方面在该拼接方法的基础上, 实现跨区域的车辆空间位置、车辆速度和交通事件监测等应用.
| [1] |
Wan YW, Huang Y, Buckles BP. Camera calibration and vehicle tracking: Highway traffic video analytics. Transportation Research Part C: Emerging Technologies, 2014, 44: 202-213. DOI:10.1016/j.trc.2014.02.018 |
| [2] |
徐德文. 基于视频的智能交通监控系统技术研究[硕士学位论文]. 西安: 西北工业大学, 2004.
|
| [3] |
Datondji SRE, Dupuis Y, Subirats P, et al. A survey of vision-based traffic monitoring of road intersections. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(10): 2681-2698. DOI:10.1109/TITS.2016.2530146 |
| [4] |
严腾. 高速公路场景下相机自动标定算法研究[硕士学位论文]. 西安: 长安大学, 2018.
|
| [5] |
王琳, 赵健康, 夏轩, 等. 基于双目立体视觉技术的桥梁裂缝测量系统. 计算机应用, 2015, 35(3): 901-904. DOI:10.11772/j.issn.1001-9081.2015.03.901 |
| [6] |
吴战广. 隧道近景摄影测量影像解析与快速实现研究[硕士学位论文]. 成都: 西南交通大学, 2016.
|
| [7] |
刘大海, 卢朝阳. 视频技术在智能交通系统中的应用. 计算机工程, 2003, 29(17): 165-166, 186. DOI:10.3969/j.issn.1000-3428.2003.17.065 |
| [8] |
Wiska R, Alhamidi MR, Habibie N, et al. Vehicle traffic monitoring using single camera and embedded systems. Proceedings of 2016 International Conference on Advanced Computer Science and Information Systems. Malang, Indonesia. 2016. 117–122.
|
| [9] |
Dubska M, Herout A, Sochor J. Automatic camera calibration for traffic understanding. Proceedings of 2014 British Machine Vision Conference. Nottingham, UK. 2014. http://www.bmva.org/bmvc/2014/papers/paper013/index.html.
|
| [10] |
Khan S, Ali H, Ullah Z, et al. An intelligent monitoring system of vehicles on highway traffic. Proceedings of the 2018 12th International Conference on Open Source Systems and Technologies. Lahore, Pakistan. 2018. 71–75.
|
| [11] |
Zheng Y, Peng SL. A practical roadside camera calibration method based on least squares optimization. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(2): 831-843. DOI:10.1109/TITS.2013.2288353 |
| [12] |
严红平, 汪凌峰, 潘春洪. 高速公路动态环境下的摄像机自标定. 计算机辅助设计与图形学学报, 2013, 25(7): 1036-1044. DOI:10.3969/j.issn.1003-9775.2013.07.014 |
| [13] |
Sochor J, Juránek R, Herout A. Traffic surveillance camera calibration by 3D model bounding box alignment for accurate vehicle speed measurement. Computer Vision and Image Understanding, 2017, 161: 87-98. DOI:10.1016/j.cviu.2017.05.015 |
| [14] |
Hong JX, Lin W, Zhang H, et al. Image mosaic based on SURF feature matching. Proceedings of the 2009 1st International Conference on Information Science and Engineering. Nanjing, China. 2009. 1287–1290.
|
| [15] |
赵向阳, 杜利民. 一种全自动稳健的图像拼接融合算法. 中国图象图形学报, 2004, 9(4): 417-422. DOI:10.3969/j.issn.1006-8961.2004.04.007 |
| [16] |
马嘉琳, 张锦明, 孙卫新. 基于相机标定的全景图拼接方法研究. 系统仿真学报, 2017, 29(5): 1112-1119. |
| [17] |
Kanhere NK, Birchfield ST. A taxonomy and analysis of camera calibration methods for traffic monitoring applications. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(2): 441-452. DOI:10.1109/TITS.2010.2045500 |
 2020, Vol. 29
2020, Vol. 29



