2. 兰州轨道交通有限公司 机电设备处, 兰州 730030
2. Department of Electromechanical Equipment, Lanzhou Rail Transit Co. Ltd., Lanzhou 730030, China
地铁门作为地铁启动频繁的部件之一, 其可靠性事关旅客安全和地铁网络调度秩序等而备受关注. 统计表明, 地铁车辆系统中列车门的故障占车辆系统总故障的约30%以上[1], 其中机械故障多于电气故障[2]. 特别地, 对于新上线且正处于新环境适应期调试的地铁车辆, 因机械装置处于磨合期或部分参数处于调试期, 系统发生故障的概率相对较高或退化变化趋势不同于成熟运行期的普遍规律. 基于此, 本文针对新上线地铁门设计了间距可调的夹紧力测量装置及故障预测模型, 以此明确地铁门早期故障发生的概率, 从而缩短新上线地铁门的调试期. 针对短期预测问题, 时间序列模型因其简易性而广受关注. 国内外许多学者开展了针对ARIMA建模相关研究与应用. 在部分振动信号缺失的情况下, 李社新[3]通过对已有数据建立ARMA时间序列模型从而恢复缺失数据, 并最终应用于某稳压泵实测振动信号中缺失数据的预测. 王民等[4]通过对磨削过程振动信号进行分析, 提出一种基于ARIMA模型的磨削颤振预测方法. 陶耀东、李宁[5]运用ARIMA模型对锂电池剩余使用寿命进行预测. 崔永祥等[6]通过建立ARMA预测模型对定轴齿轮振动信号的频谱进行预测, 同时结合预测值和当前值对齿轮故障进行预测, 预测结果将用于齿轮运行状态分析和故障预测分析. Amini等[7]通过建立ARIMA模型同时预测常规电力负荷和电动汽车停车场的充电需求. Gorlov、Strogonov[8]采用ARIMA模型对高可靠性TTL集成电路的寿命试验数据进行失效时间预测. Li等[9]根据故障率的特点, 通过建立ARMA对某航空公司波音航班的故障率进行了预测.
虽然传统的时间序列模型应用广泛, 但仍然存在预测精度低等不足. 基于此, 本文提出了改进的EMD-ARIMA预测模型. 国内外许多学者将EMD分解法应用于预测研究领域. 高强等[10]采集具有内圈损伤及外圈损伤的滚动轴承振动信号, 提出了一种基于EMD的滚动轴承故障诊断方法, 有效地提取轴承故障特征, 诊断轴承故障. 李宁等[11]为了研究飞机开关磁阻发电系统健康管理技术, 利用MATLAB软件对其典型电气故障进行了仿真分析, 然后将发电机输出电压信号利用EMD算法进行分解, 得出开关磁阻发电系统的故障预测模型. 范庚等[12]针对滑油光谱数据的非线性非平稳特性及现有预测方法的不足, 提出了一种基于EMD结合AR及RVM模型的故障磨损预测方法. Gao等[13]提出了一种基于EMD和ARMA模型对自相似网络流量进行预测的方法. Wang等[14]利用齿轮箱的振动信号将EMD分解法应用于对其的故障预测之中. Xu等[15]设计了滚动轴承加速寿命试验, 获得了轴承的所有振动信号, 然后从这些信号中提取失效特征, 并基于EMD对轴承的剩余寿命进行预测.
1 地铁门传动系统结构及工作原理地铁门按照车门的运动轨迹及与车体的安装方式可以分为: 内藏门、外挂门、塞拉门和外摆门. 本文以塞拉门传动系统作为研究对象, 其主要由基架、驱动装置、丝杆、长/短导柱、携门架等组成[16], 如图1所示.

|
图 1 传动系统结构示意图 |
驱动装置由一个直流电机和一个齿轮减速装置(减速比7∶1)组成. 丝杆是车门系统能实现开关门动作的动力传递部件. 通过三个支承丝杆被安装在基架上. 通过减速装置, 电机的旋转运动将传递到丝杆并最终带动门扇运动. 长导柱为门的纵向移动提供自由度, 短导柱承受门板的重量并为门提供横向移动自由度. 携门架通过滚珠直线轴承在长导柱上滑动将力传送到门扇[17].
传动系统是车门系统重要组成部分之一, 夹紧力可以在一定程度上反映传动系统的退化状态. 根据传动系统的工作原理可以推导出夹紧力计算公式如下:
| $F = \frac{{2{\text{π}} \eta {T_2}}}{L} = \frac{{2{\text{π}} \eta }}{L}\frac{{{Z_2}}}{{{Z_1}}}{T_1} = {\rm{ }}\frac{{19100{\text{π}} \eta {Z_2}}}{{L{Z_1}}}\frac{P}{{{n_1}}}$ | (1) |
其中, F表示地铁门夹紧力; n表示电机的输入转速; P表示轴传递的功率; n1电机轴的转速; T1表示轴传递的转矩; Z1小齿轮齿数; Z2大齿轮齿数;
地铁门开始运动时门扇处于完全打开状态, 电子门控单元接收到控制系统发出的关门指令门扇开始关闭. 同时, 地铁车门具备防夹功能即检测到障碍物时车门会打开一定开度. 如果障碍物依然存在, 将会循环一次, 循环三次后车门将完全打开.
新上线的车辆通常在组装车间完成组装, 运行车间进行调试. 此时, 传动系统处于磨合调试期, 诸如电机反馈信号等参数仍处于不断调整的阶段, 夹紧力峰值的均值也存在增大的可能. 因此, 在此期间内有必要预测其早期故障, 从而减少调试周期.
2 地铁门数据采集系统设计地铁门数据采集系统的设计主要分为采集装置的设计及软硬件电路的设计. 由于测量地铁门夹紧力的采集装置较少. 因此, 学科组研发了一种变距式自动门夹紧力测量装置. 本采集装置已申请发明专利, 专利号为201811464636.6, 其结构如图2所示.

|
图 2 地铁门夹紧力采集装置结构 |
在测力时, 通过转动左端内六角螺杆来调节左支座的位置, 使得两个测力接触端之间的距离满足需要测量的间隙. 当两个测力接触端受力时, 连杆将力传到左右支座, 左支座在螺纹锁紧下和导套向左运动, 右支座带动套筒内的弹簧导套轴端向右运动, 从而弹簧导套轴端向右压弹簧, 弹簧将力传给压力传感器(传感器通过紧贴套筒后盖), 套筒后盖和套筒通过螺纹连接, 同时套筒后盖有通孔使得导套杆可以伸缩. 从而使得压力传感器获得一个横向轴向力并将所对应的压力信号发送到数据处理终端.
与其配套的数据采集硬件系统主要由数据采集单元、数据传输单元以及数据显示单元组成. 数据采集单元将传感器接收到的压力信号通过A/D芯片转化为拟信号. 数据传输模块主要将信号通过RS-232串口通讯协议与上位机进行数据“交流”, 同时在显示单元中示数据及曲线.
软件编程部分主要包括基于STM32控制程序的编写以及基于VB开发环境的界面设计, 该部分可对检测装置所采集数据进行处理、存储、显示等工作. 数据接收界面如图3所示.
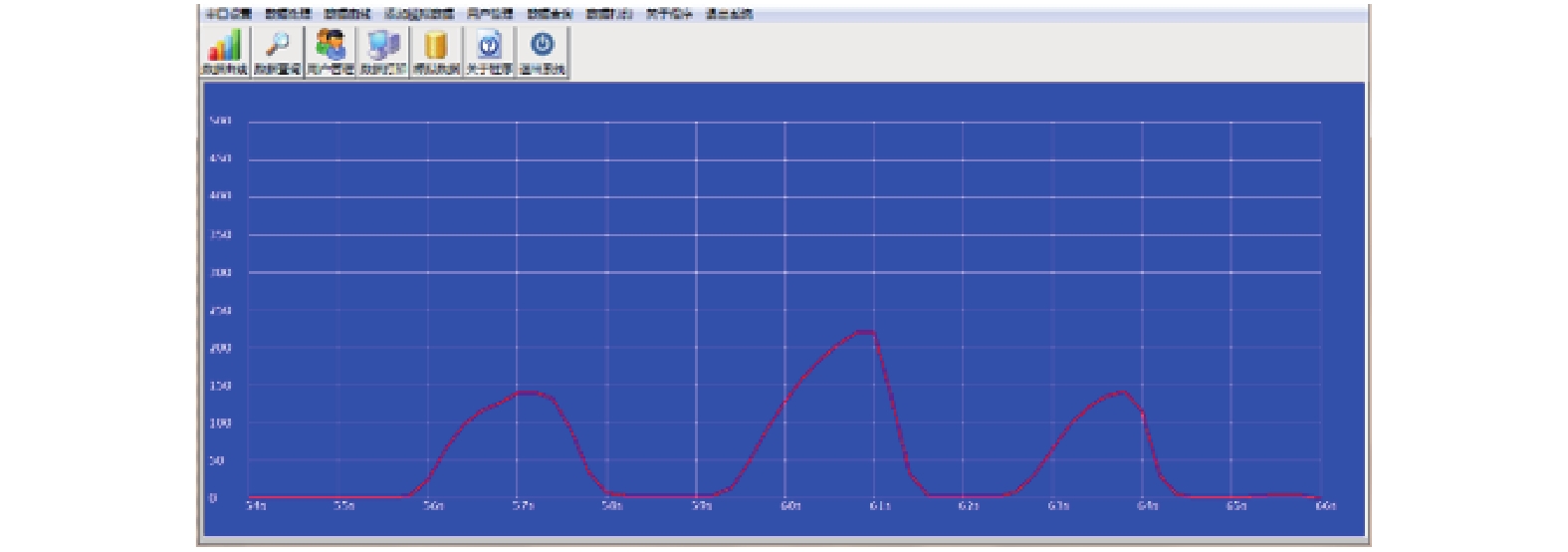
|
图 3 数据接收界面 |
3 EMD-ARIMA模型预测原理及方法 3.1 EMD分解法
经验模态分解(EMD)是一种信号变换理论, 具有自适应的特性, 分解出的信号能够很好地反映原信号的特征. EMD可以将一个信号分解为有限个本征模函数(IMF)和余量, 各IMF分量包含了原信号的不同时间尺度的局部特征信号, 从而尽可能地保留了原有数据本身的特性.
经过EMD分解时间序列X(t)被分解为n个本征模函数和一个趋势项, 可以表示为:
| $x(t) = \sum\limits_{j = 1}^n {IM{F_j}} + res.$ | (2) |
本文将EMD分解引入时间序列预测中, 把含有多个复杂的非平稳信号分解, 再对每个IMF分量利用时间序列ARIMA模型预测, 然后用各个分量的预测值重构出原始信号, 从而提高预测精准度. 预测算法如图4所示.
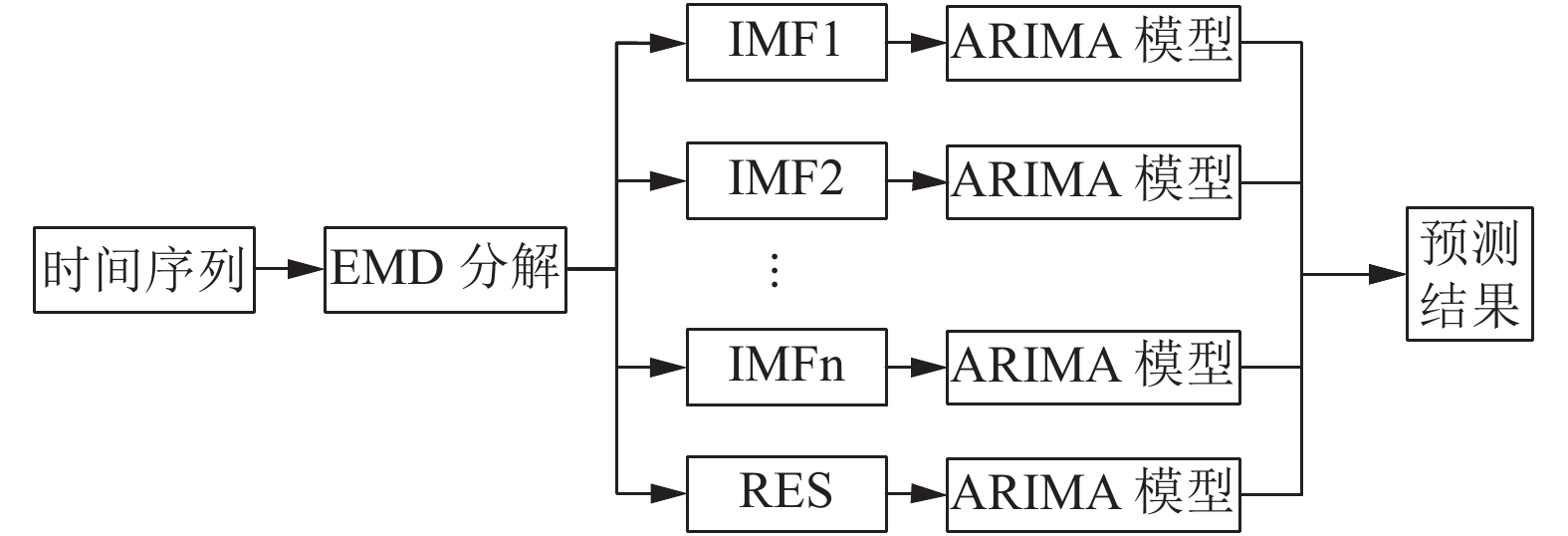
|
图 4 EMD-ARIMA预测算法 |
3.2 时间序列建模
时间序列是把预测对象的历史数据按一定的时间间隔进行排列, 构成一个随时间变化的统计序列, 建立相应的随时间变化的模型, 并将该序列外推到未来进行预测[18]. 其形式为:
| $ {X_t} = F({X_{t - 1}},{X_{t - 2}}, \cdots ,{a_t}) $ | (3) |
对于平稳序列直接采用ARMA模型进行建模, 但对于非平稳序列则需运用ARIMA模型方法进行建模, 其形式表示如下:
ARIMA(p, d, q)模型:
| ${\nabla ^d}{X_t} = {\varphi _1}{\nabla ^d}{X_{t - 1}} + \cdots + {\varphi _p}{\nabla ^d}{X_{t - p}} + {a_t} - {\theta _1}{a_{t - 1}} - \cdots {\theta _q}{a_{t - q}}$ | (4) |
为了精确确定模型阶数采用AIC准则确定模型参数. 对于ARIMA(p, d, q)模型,
对经d次差分后的时间序列运用ARMA(p,q)建模, 首先计算样本的自协方差
| $\left[ \begin{gathered} {{\hat \gamma }_{q + 1}} \\ {{\hat \gamma }_{q + 2}} \\ \vdots \\ {{\hat \gamma }_{q + p}} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {{{\hat \gamma }_q}}&{{{\hat \gamma }_{q - 1}}}& \cdots &{{{\hat \gamma }_{q - p + 1}}} \\ {{{\hat \gamma }_{q + 1}}}&{{{\hat \gamma }_q}}& \cdots &{{{\hat \gamma }_{q - p + 2}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{{\hat \gamma }_{q + p - 1}}}&{{{\hat \gamma }_{q + p - 2}}}& \cdots &{{{\hat \gamma }_q}} \end{array}} \right]\left[ \begin{gathered} {\phi _1} \\ {\phi _2} \\ \vdots \\ {\phi _p} \\ \end{gathered} \right]$ | (5) |
根据上面的公式可计算出
| $\mathop {{Z_t}}\limits^ \sim - \left({\phi _1}{\mathop Z\limits^ \sim _{t - 1}} + \cdots + {\phi _p}{\mathop Z\limits^ \sim _{t - p}}\right) = {a_t} - {\theta _1}{a_{t - 1}} - \cdots - {\theta _q}{a_{t - q}}$ | (6) |
使得:
| $\mathop {{X_t}}\limits^ \sim = \mathop {{Z_t}}\limits^ \sim - \left({\phi _1}{\mathop Z\limits^ \sim _{t - 1}} + \cdots + {\phi _p}{\mathop Z\limits^ \sim _{t - p}}\right),\;t = p + 1,p + 2, \cdots ,n$ | (7) |
最终有
模型建立后, 运用LB统计量检验法[20]对模型的有效性进行检验, LB统计量定义如下:
| ${Q_{lb}} = n\left( {n + 2} \right)\sum\limits_{k = 1}^m {\left( {\frac{{{{\hat \rho }_k}^2}}{{n - k}}} \right)} \sim {\chi ^2}\left( m \right)$ | (8) |
其中,
在轨道交通企业, 通过夹紧力测量装置分三次对处于试验阶段同一型号的地铁车辆进行地铁门夹紧力数据采集. 地铁门在关门过程中遇到障碍物会产生三次开关动作, 每一次开关动作都会产生一组数据. 在本次研究中, 夹紧力数据的峰值是预测地铁门传动系统早期故障的重要因素. 假设峰值服从正态分布, 根据所测数据峰值的均值(
本文采用Matlab对两种模型相关参数进行计算, 如图5所示为ARIMA预测模型算法流程图:
| 表 1 原始采集数据 |
由于数据存在缺失现象, 本文以10天为序列周期对原始数据进行牛顿多项式插值. 用
(1)经数据处理后, 第一次开关门动作时夹紧力峰值的均值及标准差数据如表2所示.
第一次开关门夹紧力峰值均值及标准差数据变化如图6、图7所示.
通过对数据进行ADF单根检验, 均值与标准差时间序列均为非平稳序列. 经过2次差分后再经ADF检验, 二者均为平稳序列. 然后, 通过寻找AIC最小值确定ARIMA模型中p, q值, 如表3和表4所示为不同p, q下均值及标准差AIC值.
由表3、表4可知, 当p=0, q=1时均值的AIC值最小. 当p=1, q=0时标准差的AIC值最小. 因此, 均值预测模型为ARIMA (0, 2, 1), 经计算

|
图 5 ARIMA建模算法流程图 |
| 表 2 插值后夹紧力峰值均值及标准差数据 |

|
图 6 夹紧力峰值均值变化曲线 |

|
图 7 夹紧力峰值标准差变化曲线 |
| 表 3 不同p, q下均值AIC表 |
| 表 4 不同p, q下标准差AIC值 |
综上, 峰值均值的预测模型为为
对均值及标准差进行残差的LB统计量的检验, 计算结果如表5所示.
| 表 5 模型显著性检验结果 |
由表5可知, P值显著大于0.05, 认为该拟合模型显著有效, 可以运用ARIMA模型进行预测.
在运用EMD-ARIMA模型进行预测时, 需对时间序列进行EMD分解, 最终将均值及标准差数据分解为3个IMF分量以及一个趋势项, 如图8、图9所示.
基于前面对EMD-ARIMA模型算法的分析, 通过ARIMA预测模型分别对均值及标准差的IMF1、IMF2、IMF3和趋势项进行预测. 将各项的预测数据重构得到EMD-ARIMA模型最终的预测结果, 并与ARIMA模型进行比较, 对比结果如图10、图11所示.

|
图 8 均值的EMD分解 |
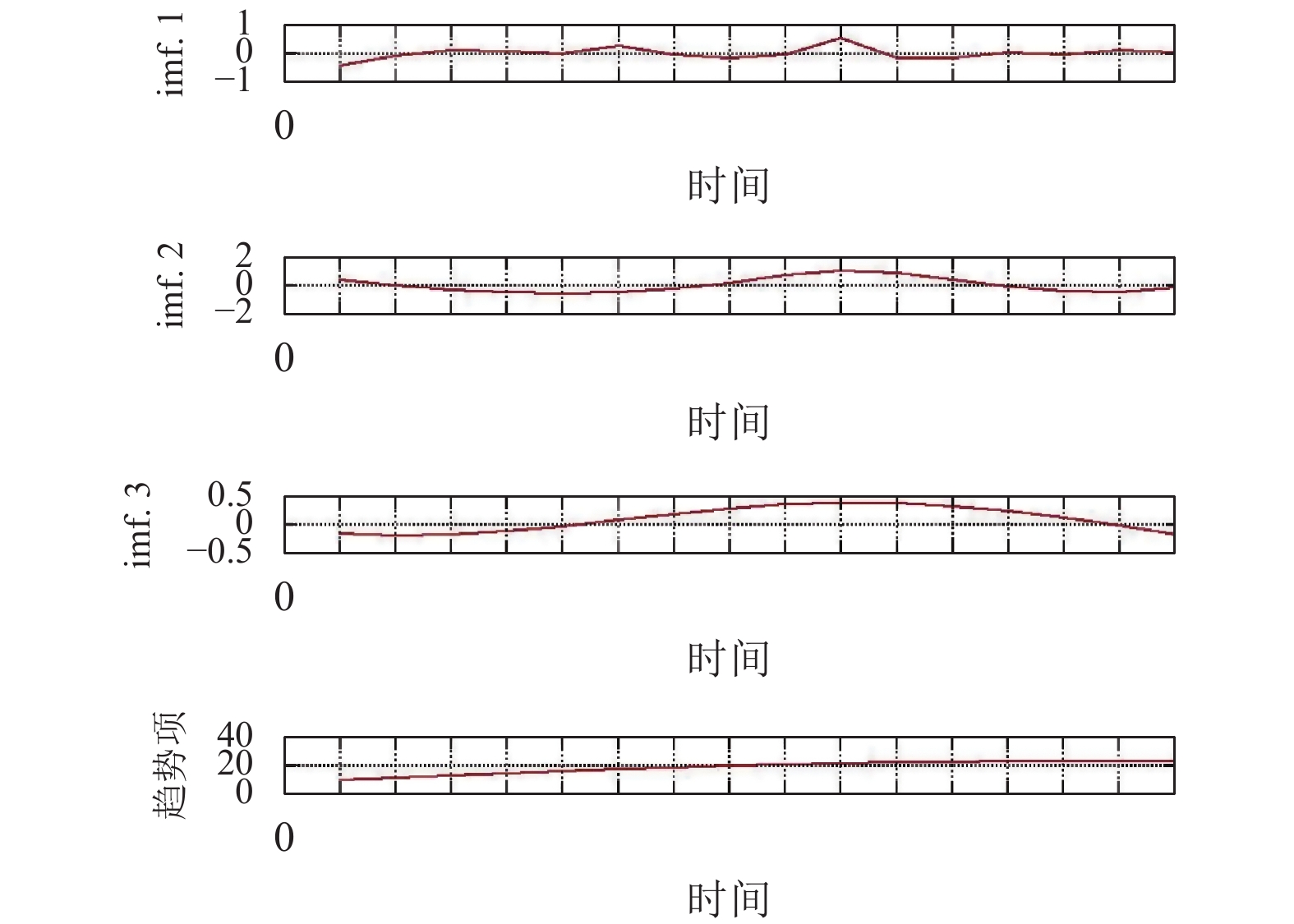
|
图 9 标准差的EMD分解 |
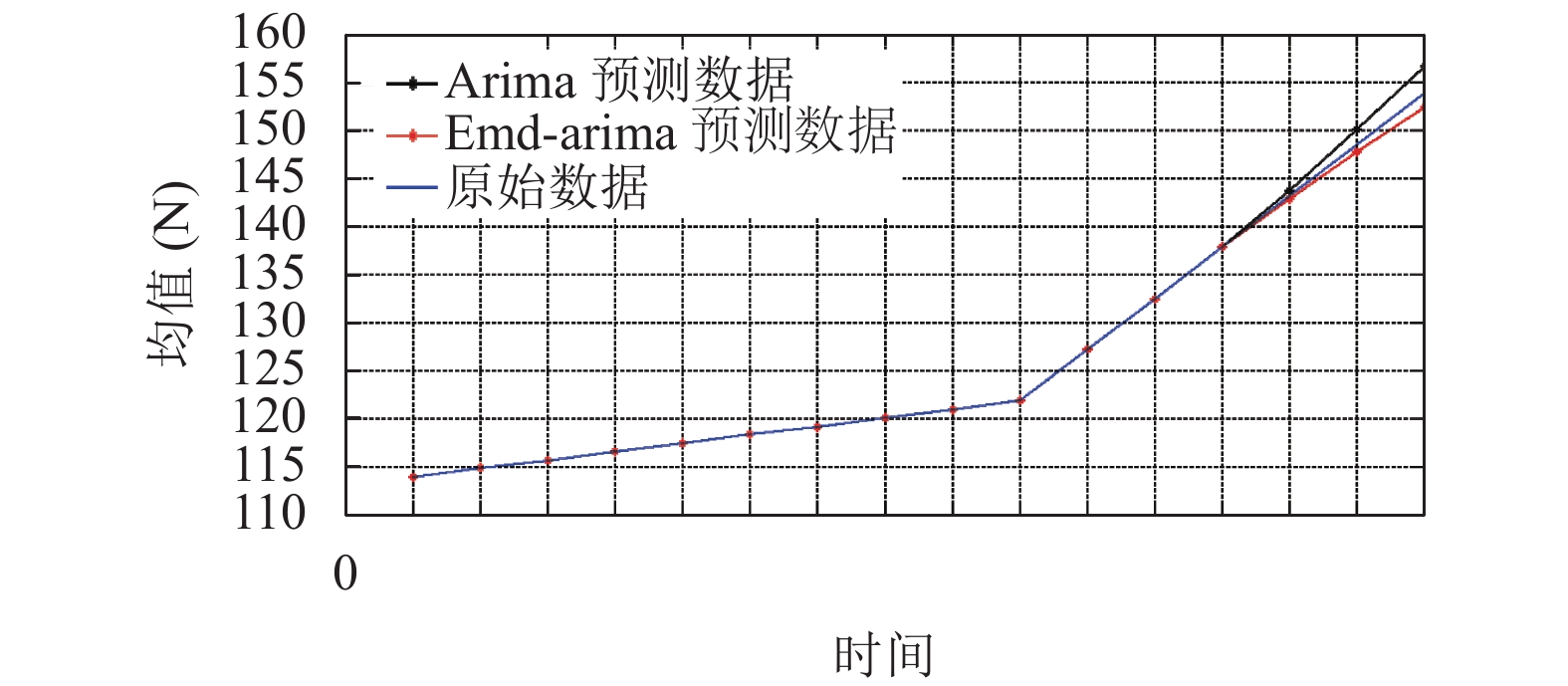
|
图 10 均值预测对比图 |

|
图 11 标准差预测对比图 |
第一次开关门夹紧力最大阈值为200 N,
| 表 6 第一次开关门ARIMA预测结果 |
| 表 7 第一次开关门EMD-ARIMA预测结果 |
(2)第二次开关门动作与第三次开关门动作夹紧力峰值分布情况的ARIMA及EMD-ARIMA模型预测步骤及方法与第一次基本相同.
通过对第二次开关门的均值据数据进行ADF单根检验, 均值为非平稳序列, 经过2次差分后为平稳序列. 标准差时间序列本身为平稳序列. 通过计算, 均值预测模型为ARIMA (0, 2, 1), 标准差预测模型为ARIMA (2, 0, 1).
综上, 峰值均值预测模型为
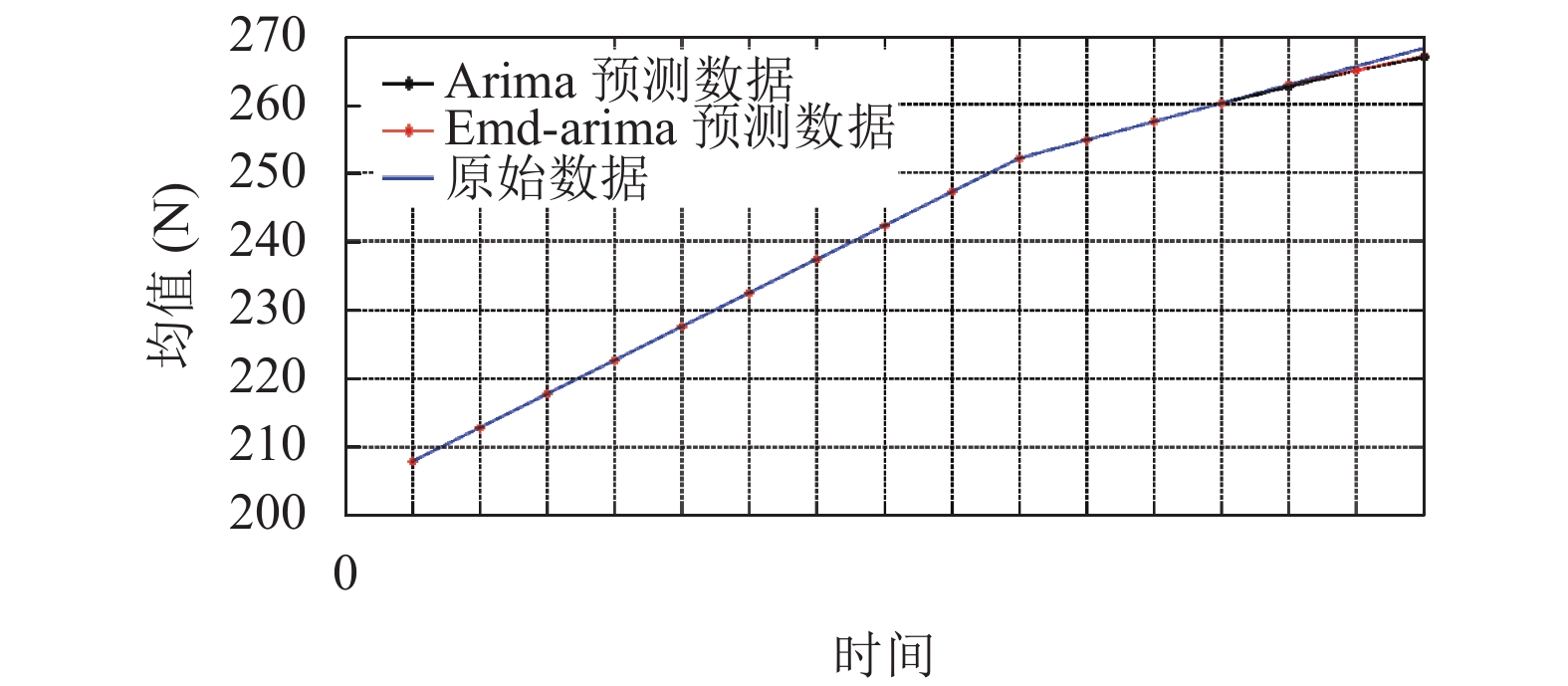
|
图 12 均值预测对比图 |
第二次开关门阈值为280 N,

|
图 13 标准差预测对比图 |
| 表 8 第二次开关门ARIMA预测结果 |
| 表 9 第二次开关门EMD-ARIMA预测结果 |
(3)通过对第三次开关门的均值及标准差数据数据进行单根检验, 均值及标准差序列为非平稳序列. 经过2次差分后, 两者均为平稳序列. 因此, 均值预测模型为ARIMA(1,2,0), 标准差预测模型为ARIMA(1,2,0). 峰值的均值预测模型为
基于EMD-ARIMA模型第三次开关门夹紧力峰值的均值及标准差预测结果如图14, 15所示.

|
图 14 均值预测对比图 |
第三次开关门阈值为300 N,
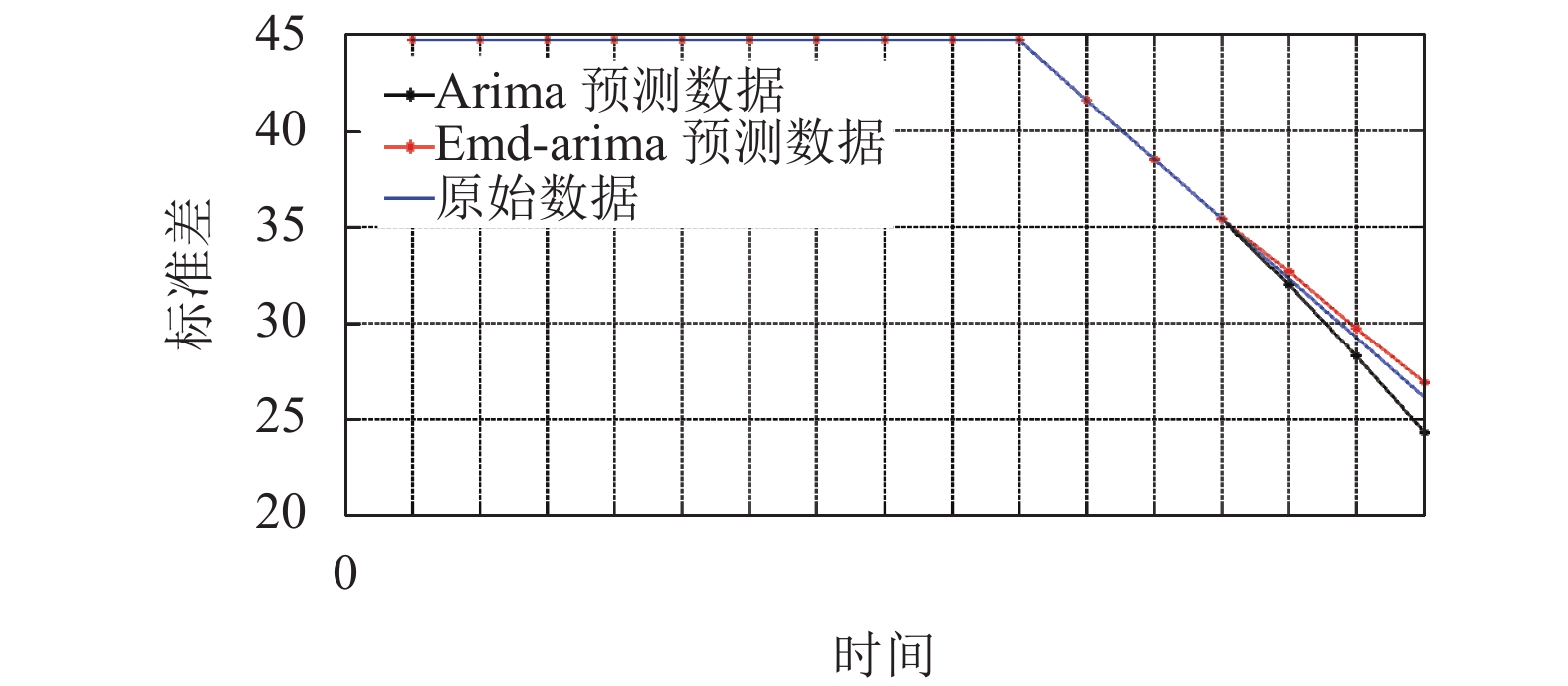
|
图 15 标准差预测对比图 |
| 表 10 第三次开关门ARIMA预测结果 |
| 表 11 第三次开关门EMD-ARIMA预测结果 |
5 结论
本文使用自主设计的数据采集系统对地铁门夹紧力数据进行采集, 并以夹紧力数据的峰值作为故障预测建模数据. 在假设所采集的夹紧力峰值数据xt服从正态分布的前提下, 应用ARIMA及改进的EMD-ARIMA模型分别对前13组数据峰值的均值及标准差进行预测, 得到未来峰值的分布, 然后根据失效阈值得到三次开关门动作时故障发生的概率.
从上述预测图表中可以清晰地看出, 相比传统的ARIMA预测模型, 改进后的EMD-ARIMA预测模型能更好地预测地铁门传动系统的早期故障. 地铁门传动系统故障概率的计算结果在一定程度上可以缩短地铁门的调试周期, 为轨道交通企业在地铁门调试期间的检测和维护提供理论基础和技术支持, 丰富和完善关于调试期间地铁门故障预测理论, 着力解决企业面临的相关问题.
| [1] |
王冬雷. 广州地铁四号线车辆塞拉门系统的特点及常见故障分析. 电力机车与城轨车辆, 2006, 29(6): 44-46. DOI:10.3969/j.issn.1672-1187.2006.06.015 |
| [2] |
夏军, 任金宝. 地铁车门故障模式的可靠性评估. 机械制造与自动化, 2014, 43(5): 185-188. DOI:10.3969/j.issn.1671-5276.2014.05.060 |
| [3] |
李社新. ARMA模型在振动信号分析中的应用. 机械科学与技术, 2010, 29(11): 1586-1588. |
| [4] |
王民, 冯猛, 姚子良, 等. 基于ARIMA的磨削颤振预测方法. 北京工业大学学报, 2016, 42(4): 609-613. DOI:10.11936/bjutxb2015070030 |
| [5] |
陶耀东, 李宁. 基于ARIMA模型的工业锂电池剩余使用寿命预测. 计算机系统应用, 2017, 26(11): 282-287. |
| [6] |
崔永祥, 陈磊, 韩捷, 等. 时序分析在定轴齿轮故障预测中的应用研究. 机械设计与制造, 2017(12): 11-13. DOI:10.3969/j.issn.1001-3997.2017.12.003 |
| [7] |
Amini MH, Kargarian A, Karabasoglu O. ARIMA-based decoupled time series forecasting of electric vehicle charging demand for stochastic power system operation. Electric Power Systems Research, 2016, 140: 378-390. DOI:10.1016/j.jpgr.2016.06.003 |
| [8] |
Gorlov MI, Strogonov AV. ARIMA models used to predict the time to degradation failure of TTL ICs. Russian Microelectronics, 2007, 36(4): 261-270. DOI:10.1134/S1063739707040063 |
| [9] |
Li RY, Kang R. Research on failure rate forecasting method based on ARMA model. Systems Engineering and Electronics, 2008, 30(8): 1588-1591. |
| [10] |
高强, 杜小山, 范虹, 等. 滚动轴承故障的EMD诊断方法研究. 振动工程学报, 2007, 20(1): 15-18. DOI:10.3969/j.issn.1004-4523.2007.01.003 |
| [11] |
李宁, 雷洪利, 韩建定, 等. 飞机开关磁阻发电系统故障推理模型研究. 电源技术, 2011, 35(5): 563-566. DOI:10.3969/j.issn.1002-087X.2011.05.025 |
| [12] |
范庚, 马登武. 基于EMD和RVM-AR的航空发动机磨损故障预测模型. 计算机测量与控制, 2013, 21(7): 1746-1749. DOI:10.3969/j.issn.1671-4598.2013.07.007 |
| [13] |
Gao B, Zhang QY, Liang YS, et al. Predicting self-similar networking traffic based on EMD and ARMA. Journal on Communications, 2011, 32(4): 47-56. |
| [14] |
Wang JZ, Zhou GH, Zhao XS, et al. Gearbox fault diagnosis and prediction based on empirical mode decomposition scheme. Proceedings of 2007 International Conference on Machine Learning and Cybernetics. Hong Kong, China. 2007. 1072–1075.
|
| [15] |
Xu D, Xu YC, Chen X, et al. Life cycle vibration analysis based on EMD of rolling element bearing under alt by constant stress. Proceedings of the 8th International Conference on Reliability, Maintainability and Safety. Chengdu, China. 2009. 1177–1182.
|
| [16] |
黄冬. 轨道车辆门可靠性数据管理及故障分析系统的研究与实现[硕士学位论文]. 南京: 南京理工大学, 2007.
|
| [17] |
曾庆虎. 机械传动系统关键零部件故障预测技术研究[博士学位论文]. 长沙: 国防科学技术大学, 2010.
|
| [18] |
Kjolle GH, Gjerde O, Hjartsjo BT, et al. Protection system faults -- a comparative review of fault statistics. Proceedings of 2006 International Conference on Probabilistic Methods Applied to Power Systems. Stockholm, Sweden. 2006.
|
| [19] |
Zhang Q, Wang BD, He B, et al. Singular spectrum analysis and ARIMA hybrid model for annual runoff forecasting. Water Resources Management, 2011, 25(11): 2683-2703. DOI:10.1007/s11269-011-9833-y |
| [20] |
杜奕. 时间序列挖掘相关算法研究及应用[博士学位论文]. 合肥: 中国科学技术大学, 2007.
|
 2019, Vol. 28
2019, Vol. 28



