2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
对称矩阵的特征求解问题在科学计算领域普遍存在, 包括计算物理、计算化学、结构力学、纳米材料等前沿学科. 通常的处理方法是先通过正交变换把原矩阵化为三对角矩阵, 如使用Householder或Givens方法, 再求解三对角阵的特征值和特征向量, 然后映射回原矩阵的特征值和特征向量. 三对角阵的特征求解算法有很多种, 常见的有QR法、二分法、MRRR方法和分而治之方法等等. 由于QR法和二分法求解特征向量时往往需要显式的正交过程, 时间复杂度为O(n3), 常用于中小规模矩阵的特征求解. 而分治法和MRRR法能避免这一过程, 分治法的平均时间复杂度仅为O(n2.3), 其分而治之思想对于大规模矩阵特征问题的并行求解求解有着天然的优势.
分而治之求解对称三对角矩阵特征问题的算法最早由Cuppen提出[1], 后M. Gu和S. C. Eisenstat等人作出改进, 提高了该算法求解的特征向量的正交性[2], 使得该算法能够在实际求解中应用. 该算法采用分而治之思想, 将原矩阵划分为若干子矩阵, 先求出子矩阵的特征分解, 再通过修正计算, 逐级合并子矩阵的结果, 回代得到原矩阵的特征分解. 分治法具有很强的灵活性, 适合大规模三对角矩阵特征问题求解的并行化求解.
分治算法的并行化工作很早就开始展开[3–5], 如基于分布式存储的MPI进程级并行, 基于共享内存的openMP线程级并行, 还有基于SMP的MPI/openMP混合并行等模型. 并行化的实现主要基于数据并行的考量, 通过划分数据到多个核或节点上计算, 在负载均衡的条件下能取得较好的并行效果. 但对于分治和递归类的场景, 当数据依赖呈现复杂的网状结构时, 难以实现理想的负载均衡效果.
基于任务的并行编程模型按照功能将一个应用划分成多个能并行执行的模块, 可以是细粒度的, 也可以是粗粒度的. 常见的任务并行模型有TBB,Cilk和SMPSS等, 使用这些模型时无需关心任务的具体分配和调度细节.
Cilk作为一个基于任务的并行编程模型, 为共享内存系统提供了一个高效的任务窃取调度器, 适合用来为分治和递归类算法实现高效的多核任务并行. 对于并行编程, Cilk为串行程序的并行化提供了向量化、锁、视图等机制[6], 通过关键字来声明操作, 改造后的代码具有语义化、可读性强的特点.
1 分治算法求解的基本原理 1.1 矩阵划分对任意n阶实对称三对角矩阵T, 基于秩1修正从第k行作如下划分:
| $\begin{split} T &= \left( {\begin{array}{*{20}{c}} {{T_1}}&{\beta {e_k}e_1^{\rm{T}}} \\ {\beta {e_1}e_k^{\rm{T}}}&{{T_2}} \end{array}} \right) \\ &= \left( {\begin{array}{*{20}{c}} {{{T'}_1}}&0 \\ 0&{{{T'}_2}} \end{array}} \right) + \beta \left( {\begin{array}{*{20}{c}} {{e_k}} \\ {{e_1}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {e_k^{\rm{T}}}&{e_1^{\rm{T}}} \end{array}} \right) \\ \end{split} $ | (1) |
其中, T'1, T'2是三对角子矩阵块, ek代表第k个元素为1的单位向量, 元素β是T的第k个副对角元素. 为使修正矩阵元素一致, 对T1的末位元素和T2的首元素都减去了相同的元素.
分治过程一般采用折半划分, 对于划分后的矩阵T', 若规模未达到指定阈值, 则继续划分.
1.2 分治法求解过程若划分后的子矩阵规模达到设定阈值, 调用QR或者其他算法得到子矩阵T’1, T’2的特征值分解:
| ${T'_1} = {Q_1}{D_!}{Q_1}^{\rm{T}},{T'_2} = {Q_2}{D_2}{Q_2}^{\rm{T}}$ | (2) |
令修正向量
| $z = diag{\left( {{Q_1},{Q_2}} \right)^{\rm{T}}}\left( {\begin{array}{*{20}{c}} {{e_k}} \\ {{e_1}} \end{array}} \right),$ | (3) |
则矩阵T的特征分解如下:
| $\begin{split} T &= \left( {\begin{array}{*{20}{c}} {{Q_1}}&0\\ 0&{{Q_2}} \end{array}} \right)\left[ {\left( {\begin{array}{*{20}{c}} {{D_1}}&{}\\ {}&{{D_2}} \end{array}} \right) + \beta z{z^{\rm{T}}}} \right]{\left( {\begin{array}{*{20}{c}} {{Q_1}}&0\\ 0&{{Q_2}} \end{array}} \right)^{\rm{T}}}\!\!\!\!\!\!\!\!\!\\ &= Q\left( {D + \beta z{z^{\rm{T}}}} \right){Q^{\rm{T}}}. \end{split}$ | (4) |
令D+βzzT=W, 因为diag(Q1, Q2)为正交矩阵, 所以T和W相似有相同的特征值, 求T的特征分解T=QΛQT, 可以通过先求出W的特征分解: W=PΛPT, 再令Q=diag(Q1, Q2)P, 即可求得T的特征分解.
对于W的特征分解, 需要根据划分后矩阵的特征值和原矩阵特征值之间的间隔性[7], 通过求解对应的secular方程(3):
| $1 + \beta \sum\limits_i {\frac{{x_i^2}}{{{d_i} - \lambda }}} = 0,{d_i} = {D_{ii}}$ | (5) |
得到相应的的特征值λ. 文献[6]讨论了方程(3)根的分布特性和解法, 在特征区间内使用牛顿法或拉格朗日法迭代逼近区间内的特征值, 线性时间内即可收敛. 解出所有的特征值后, 再通过式(D−λI)−1x[1]求得每个特征值对应的特征向量, 回代到式(1)中得到T的特征分解.
整个求解过程在逻辑上可看作树型结构, 在叶子结点上进行特征求解, 在非叶子结点上进行特征合并.
1.3 注意事项文献[5]中指出合并过程中如果D的主对角线上出现了相同的元素或者z向量中出现0元素时, 在迭代前进行deflation操作可以避免特征区间内迭代不收敛的情况. 通过Givens正交旋转变换, 部分特征值和特征向量就能原地得到. 如果求得的特征值前后过于接近, 按原方法求得的特征向量会丢失正交性, 文献[8,9]讨论了特征值间隔过小时的特征向量的求法, 避免了显式正交过程. 文献[2]根据特征问题的反问题给出了特征向量的改进求法, 保证了计算结果的正交性.
2 分治算法的并行化 2.1 节点内并行实现单节点内求解三对角矩阵块的特征分解主要包含两个过程, 分别是求出最小划分矩阵的特征分解以及逐步合并特征值和特征向量. 由于每个子矩阵的特征计算以及同级子矩阵之间的合并过程是相互独立的, 下面结合Cilk模型给出递归实现的分治算法在单节点多核环境下的并行化算法.
算法1. 分治算法基于Cilk的节点内并行
1) 判断输入矩阵的规模, 如果矩阵规模小于等于设定 阈值, 执行2); 否则执行3);
2) 调用特征求解算法进行特征分解, 返回结果;
3) 划分矩阵T得子矩阵T1, T2, 通过Cilk执行任务划分, 并行地对T1, T2递归调用步骤1), 求出子矩阵的特征值和特征向量后, 进行排序和迭代逼近等操作合并子矩阵的特征值和特征向量, 得到T的特征分解, 返回结果.
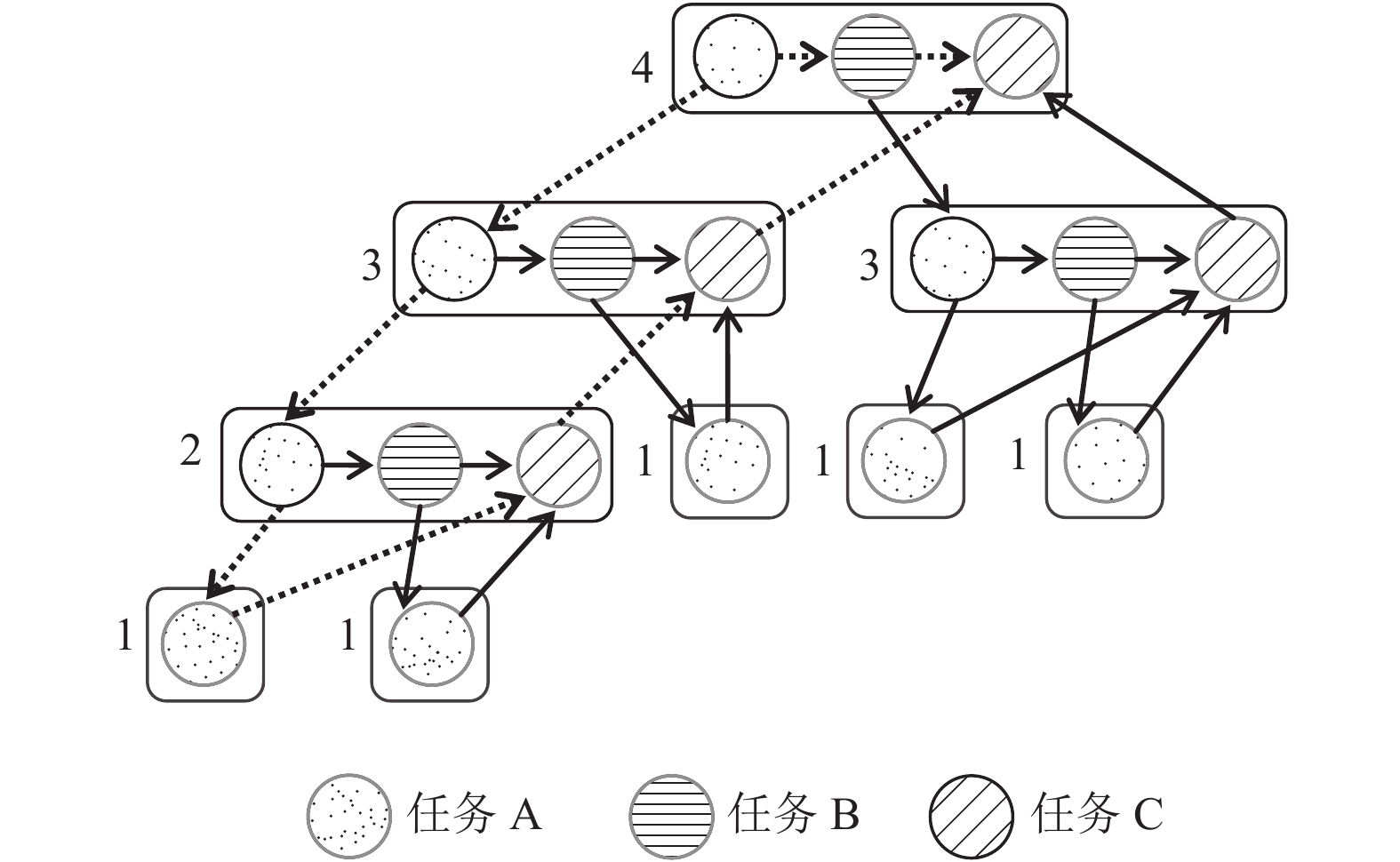
Cilk在程序递归执行过程中不断划分新的任务, 产生Cilk线程去处理, 并把其分配到空闲的核上, 和父线程并行执行. 一个Cilk任务是在同步、生成新线程或返回结果之前执行的最长序列化指令集或代码段[10]. 求解过程中, 递归调用T1之前的过程可看作任务A, 递归调用T2的过程可看作任务B, 同步及合并过程可看作任务C. 现假设程序只进行了四次嵌套调用, 则全局任务划分后生成的任务流如图1所示.
2.2 多节点混合并行实现实现分治算法的多节点并行, 需要先把原始矩阵按逻辑树结构划分成小的子矩阵分发到叶子结点上进行初步计算, 然后通过MPI通信汇总每棵子树的计算结果, 把整理后的结果重新发送到子结点进行合并操作, 重复此过程, 直到返回到树的根结点. 为了减少进程间通信, 充分利用Cilk任务并行机制, 需要对原矩阵进行较粗粒度的划分, 以榨取单节点处理器的计算性能.
|
图 1 分治算法的任务并行流程 |
对于n阶对称三对角矩阵T在N个进程上的特征求解, 假设N=2k, n=2j, 算法初始时把原矩阵划分为N个子矩阵, 每个子矩阵阶数为2j–k, 下面给出分治算法在多节点上的混合并行实现.
算法2. 分治算法基于MPI/Cilk的节点间并行
首先, 对于划分到N个进程上的每个初始子矩阵, 调用算法1求出各部分特征值和特征向量;
接着, 进行p轮循环(p对应逻辑树的高度). 每轮循环先把进程分组并确定主控进程. 每个MPI进程根据自己的进程类别按序选择执行下列步骤:
1) 组内进程通过互补通信交换求得的局部特征向量矩阵, 接着向主控进程发送本进程求得的局部特征值和拼接的修正向量;
2) 主控进程收集所有组内进程求得的局部特征值进行排序, 并保留排序后的位置索引数组, 并根据此数组将修正向量排序, 将排好序的特征值和修正向量划分到组内各进程;
3) 组内进程接收主控进程发送过来的排好序的部分特征值和修正向量, 求解secular方程和特征向量;
4) 各组内进程按列执行分块矩阵乘法, 更新当前轮循环的部分特征向量矩阵, 接着执行下一轮循环.
2.3 算法分析图1最上方左面对应递归的最外层, 每个出度大于1的结点都会派生出新的Cilk线程, 执行新的任务. 程序执行过程产生的所有的Cilk线程数为图1中节点数, 关键路径长度为图1中虚线部分路径长度. 程序的并行性为Cilk线程数与关键路径长度之比, 执行时间大于等于所有任务平均到每个核上运行的时间和关键路径上任务运行花费的总时间.
算法2中在对特征值进行排序后, 同时记录排序后各位置元素的原来位置的索引, 避免对特征向量重复排序, 方便下一轮特征向量的计算. 在第p轮循环中, 从0号进程开始每2p+1个进程分为一组, 每隔2p+1个进程被选为选为主控线程. 更新局部特征向量矩阵时, 为了减少数据通信开销, 避免主控进程进行统一收发, 使组内进程间只进行必要的局部特征向量的互补交换, 然后按列执行分块矩阵乘法, 分别计算更新的特征向量矩阵的部分, 通信量为O(n2/N).
算法1和算法2中的合并过程涉及大量计算密集型操作, 占据程序执行的主要时间, 可以使用Cilk提供的数据并行机制加速. Cilk通过数据划分形成一个个可供调度的线程级任务并行执行, 通过基于贪心策略的任务窃取方式执行调度: 当一个核完成自己的任务而其它核还有很多任务未完成, 此时会将忙的核上的任务重新分配给空闲的核.
由于在迭代计算不同特征值的近似值时, 所执行的迭代次数可能不同, 均匀分配任务可能导致线程间的负载不平衡. Cilk通过工作密取机制从其他线程获取一部分工作量, 能够避免单核上出现任务过载和饥饿等待的问题, 同时能将密取的次数控制在最低水平, 减少密取带来的性能开销. 若单节点内划分的数据粒度适当, 就能利用Cilk机制充分发挥多核处理器的计算和调度能力, 得到较好的负载均衡.
3 实验结果与分析我们在中科院“元”超算上的cpuII计算队列进行了数值实验, 节点上搭载的是Intel E5-2680 V3芯片, 每块芯片包含12颗主频为2.5 GHz的计算核心. MPI程序使用Intel mpiicpc编译并链接到Cilk Plus运行时. 实验对象是30 000阶主对角元素是4, 副对角元素是1实对称三对角矩阵. 矩阵划分求解的规模阈值设为200阶, 实验最终求出全部特征值和特征向量(通过环境变量设置每个节点使用2~12个Cilk线程进行实验).
表1是MPI模型与MPI/Cilk混合模型在4~128个核、2~12个Cilk线程参与计算下所用时间汇总. 从表中可以看出, 相同计算条件下MPI/Cilk混合并行计算时间要少于纯MPI方法, 而随着参与计算的Cilk线程数的增加, 计算用时也越来越少, 这表明当计算任务密集时, 计算效率随着可供调度的线程的增加而增加. 当参与计算的Cilk线程数超过10时, 对于当前规模的矩阵计算获得的加速提升效果逐渐变得有限, 这是因为Cilk是基于贪心策略执行调度的, 当任务粒度较小时不会频繁的执行任务窃取, 从而减小系统开销. 而在较少节点参与计算时, 获得的加速效果较为明显, 这说明对数据进行粗粒度划分时能取得较好性能.
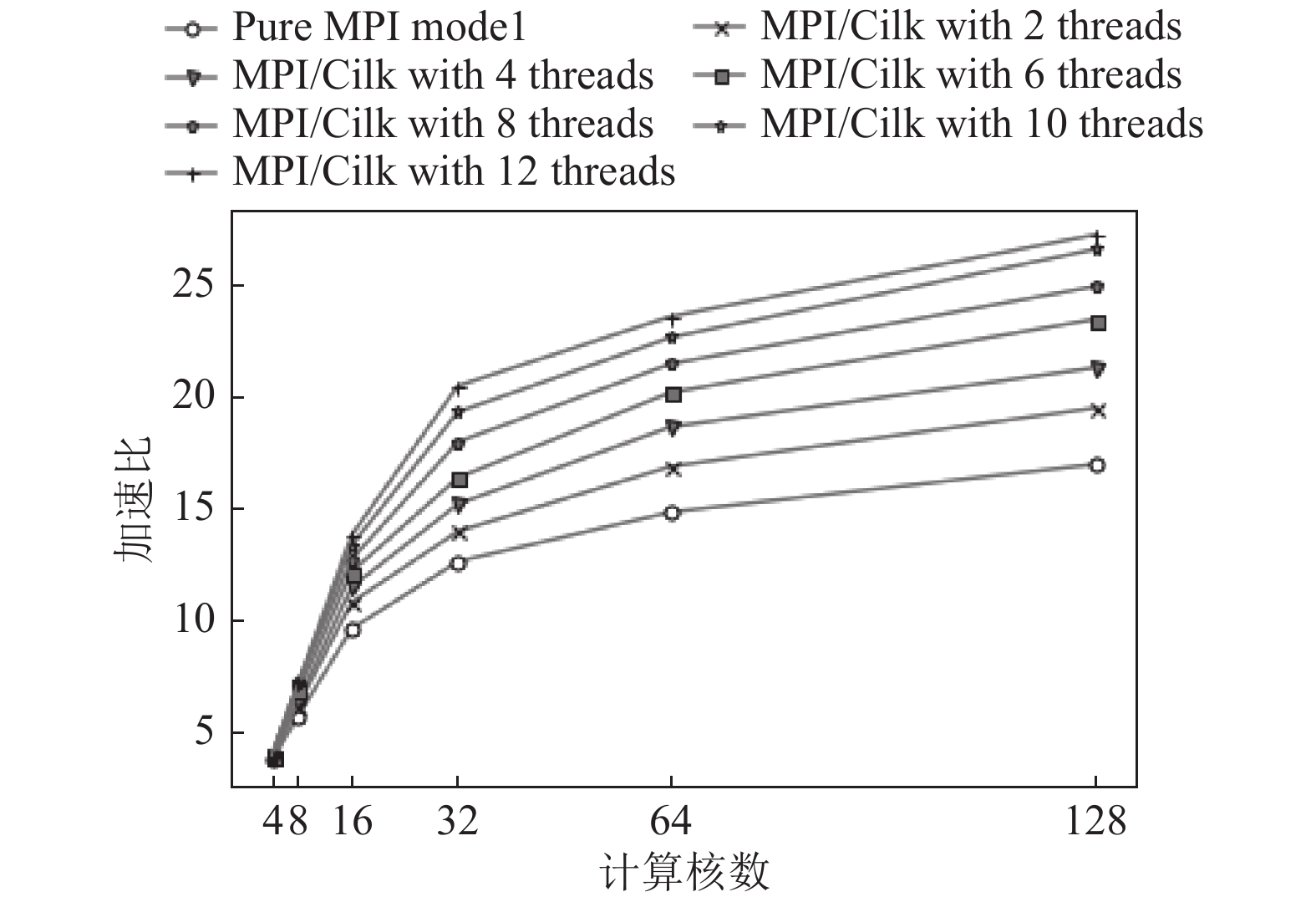
图2是MPI模型和MPI/Cilk模型在不同参数下的加速比变化趋势曲线(已测出在单节点单线程环境下的平均串行时间为880秒左右). 可以看出, 随着参与计算的核数和Cilk线程数增加, 三条曲线的上升趋势都逐渐变得平缓, 出现这种现象的原因主要为计算任务粒度变细和进程间通信开销增加导致的. MPI/Cilk方法的曲线在一开始上升较快, 随着进程数的增加, 计算任务粒度逐渐减小, 加速效果也随之下降, 但仍比纯MPI方法变缓得更慢. 这表明MPI/Cilk方法的并行效果要优于纯MPI方法, 拥有更好的可扩展性. 随着可供调度的核数增多, 使用更多的Cilk线程数参与计算能获得更好的计算性能, Cilk动态调度的优势也渐渐体现了出来.
表2给出了MPI/Cilk模型(使用8个Cilk线程)同ELPA、ScaLAPACK软件包实现的分治算法求解30000阶矩阵特征的计算时间比较. ELPA和ScaLAPACK是求解线性代数问题领域中应用广泛的并行软件包. 从表中数据可以得出, 当参与计算的核数较少时, MPI/Cilk方法与ELPA、Scalapack中分治算法计算用时接近, 随着参与计算的核数增多, MPI/Cilk方法、ELPA方法与ScaLAPACK方法的计算性能逐渐拉开, 但本文的MPI/Cilk方法与ELPA方法的扩展性仍然存在着一定差距. 这是由于ELPA按照块级循环分布矩阵, 实现了对计算流程的更细粒度的控制.
| 表 1 MPI模型和MPI/Cilk模型运行时间 |
|
图 2 MPI模型和MPI/Cilk模型的加速比曲线 |
| 表 2 MPI/Cilk方法与ELPA、ScaLAPACK求解器时间对比 |
4 结论与展望
本文针对对称三对角矩阵特征求解的分治算法, 提出了一种改进的基于MPI/Cilk的混合并行实现. 在节点间, 进行粗粒度计算任务的划分, 更新局部特征矩阵时通过弱化主控进程的中心作用, 使组内进程之间只进行必要的互补数据交换, 避免了统一收发流程, 减少了进程间的通信开销; 在节点内, 利用Cilk的任务并行机制提高了CPU的利用率和特征求解过程中的负载均衡性. 实验结果体现了该算法的性能. 本文实现的分治算法与最新的ELPA软件包仍然存在一定的性能差距, 还有可以提升的空间. 此外, Cilk线程启动数和数据划分粒度对计算性能的影响以及同openMP等其它任务并行模型的效果对比等等是值得进行下一步研究的方向.
| [1] |
Cuppen JJM. A divide and conquer method for the symmetric tridiagonal eigenproblem. Numerische Mathematik, 1980, 36(2): 177-195. DOI:10.1007/BF01396757 |
| [2] |
Gu M, Eisenstat SC. A stable and efficient algorithm for the rank-one modification of the symmetric eigenproblem. SIAM Journal on Matrix Analysis and Applications, 1994, 15(4): 1266-1276. DOI:10.1137/S089547989223924X |
| [3] |
Tisseur F, Dongarra J. A parallel divide and conquer algorithm for the symmetric eigenvalue problem on distributed memory architectures. SIAM Journal on Scientific Computing, 1998, 20(6): 2223-2236. |
| [4] |
Zhao YH, Chen J, Chi XB. Solving the symmetric tridiagonal eigenproblem using MPI/OpenMP hybrid parallelization. Cao J, Nejdl W, Xu M. Lecture Notes in Computer Science. Berlin: Springer, 2005. 3756. 164–173.
|
| [5] |
Ammar GS, Reichel L, Sorensen DC. An implementation of a divide and conquer algorithm for the unitary eigen problem. ACM Transactions on Mathematical Software, 1992, 18(3): 292-307. DOI:10.1145/131766.131770 |
| [6] |
Intel Cilk Plus. Intel Cilk reference manual and documentation, https://www.cilkplus.org/cilk-plus-tutoriall.
|
| [7] |
Melman A. Numerical solution of a secular equation. Numerische Mathematik, 1995, 69(4): 483-493. DOI:10.1007/s002110050104 |
| [8] |
Dhillon IS, Parlett BN. Orthogonal eigenvectors and relative gaps. SIAM Journal on Matrix Analysis and Applications, 2003, 25(3): 858-899. DOI:10.1137/S0895479800370111 |
| [9] |
Dhillon IS, Parlett BN. Multiple representations to compute orthogonal eigenvectors of symmetric tridiagonal matrices. Linear Algebra and its Applications, 2004, 387: 1-28. DOI:10.1016/j.laa.2003.12.028 |
| [10] |
Supercomputing Technologies Group, MIT Laboratory for Computer Science. Cilk-5.4.6 reference manual. Cambridge, Massachusetts, USA: Massachusetts Institute of Technology. http://supertech.csail.mit.edu/cilk/manual-5.4.6.pdf.
|
 2019, Vol. 28
2019, Vol. 28



