2. 西北师范大学 教育学院, 兰州 730070
2. College of Education, Northwest Normal University, Lanzhou 730070, China
数据挖掘(DM, Data Mining)是近年来研究、开发和应用最活跃的一个领域, 它是在机器学习、神经网络和模式识别的理论基础上发展而来的, 其任务是从海量数据中提取隐含且用户感兴趣的知识和信息[1].
关联规则挖掘是数据挖掘中最重要的研究领域之一, 其本质是对频繁模式的挖掘, 最早由Agrawal等提出[2], 目的是发现模式之间隐含的内在联系, 为后续问题的解决提供决策支持. 关联规则挖掘主要包含两个子问题: 一是生成频繁模式集, 其任务是根据用户设置的最小支持度阈值生成所有频繁模式; 另一个是生成关联规则, 主要任务是从所有的频繁模式中提取满足最小置信度阈值的规则.
频繁模式挖掘算法大致可分为两类: 一种是类Apriori算法, 如文献[3]提出了Inter-Apriori频繁模式挖掘算法, 该算法使用交集策略来减少扫描数据库的次数, 使算法达到了较高的效率; 文献[4]提出了一种基于三角矩阵和差集的垂直数据格式挖掘频繁模式的算法; 文献[5]提出了一种基于前缀项集的候选集存储结构, 并利用哈希表进行快速查找, 提高了经典Apriori算法在连接步和剪枝步中的效率; 文献[6]提出了一种基于矩阵的改进算法, 通过事务矩阵和候选项集项目矩阵相乘的矩阵操作改进频繁扫描数据库的问题, 优化了Apriori算法的连接步与剪枝步. 这些算法都是由经典的Apriori算法改进而来, 由于Apriori算法的固有缺陷, 使得这些算法的挖掘效率仍然不高. 另一类是基于频繁模式增长的算法, 如文献[7]提出了一种基于频繁模式树(FP-tree)的FP-growth算法; 文献[8]提出了一种基于COFI-Tree挖掘N-最有兴趣项集算法, 该算法采用COFI-Tree结构, 无需递归构造条件子树FP-Tree; 文献[9]提出了一种基于邻接表的改进FP-Growth算法, 该算法使用哈希表存储邻接表, 可以快速删除小于最小支持阈值的模式. 这类算法利用树结构对数据库进行压缩, 不产生候选项集, 减少了数据库的扫描次数, 但在对大型稠密数据集进行挖掘时会构造大量条件模式基和条件FP-tree, 对内存消耗非常大.
为克服前两类算法的局限性, 一些研究人员将Apriori算法和FP-tree结构结合[10–14]. 这类算法先将整个数据库投影到FP-tree上, 然后对FP-tree进行分区, 将数据库划分成若干个子数据集, 最后利用Apriori算法的候选生成-测试机制对子数据集进行挖掘. 文献[10]首次将Apriori算法与FP-tree结合, 提出了相应的APFT算法, 该算法不需要递归地生成条件模式基和条件FP-tree, 有效提高了挖掘效率. 文献[11]在FP-tree的基础上提出了压缩频繁模式树(CFP-tree), 并从最不频繁的项开始划分生成子树, 并在每棵子树上执行候选项集生成机制, 算法避免了递归生成大量子树, 提高了模式挖掘速度; 文献[12]利用频繁1-项集对数据库进行分库, 统计候选项集支持度计数时只扫描分库, 减少了Apriori算法对数据库的遍历次数; 文献[13]提出了一种改进的基于fp-tree的Apriori算法, 该算法先用尾元将fp-tree分区, 生成数据量更小的子数据集, 再动态删除冗余数据将子数据集进一步压缩, 最后通过扫描子数据集进行支持数统计; 文献[14]将Apriori算法与FP-growth算法结合, 提出了一种基于事务映射区间求交的频繁模式挖掘算法IITM, 只需扫描数据集两次来生成FP-tree, 然后扫描FP-tree将每个项的ID映射到区间中, 通过区间求交进行模式增长. 但将FP-tree结构与Apriori算法结合后仍存在以下不足: (1) Apriori算法在连接步会花费大量时间判断项集是否满足连接条件; (2) 构建FP-tree时需要对数据库进行两次扫描, 且不支持交互式挖掘与增量挖掘.
为解决这些问题, 本文在APFT算法的基础上提出了一种改进的频繁模式挖掘算法. 主要进行了如下改进: (1)在算法的连接步前加入预处理过程, 减少比较次数; (2)提出了一种新的紧凑前缀树结构, 只需对数据库进行一次扫描就可以构造出一棵紧凑的模式树, 且支持交互式挖掘与增量挖掘, 能有效处理数据流问题.
1 问题陈述 1.1 频繁模式挖掘设
频繁模式挖掘定义为, 在给定的数据库D和最小支持度阈值
Apriori算法[2]最早由Agrawal等提出, 该算法使用先验性质压缩搜索空间, 并使用一种逐层搜索的迭代方法, 其中
连接步: 这一步主要是为了生成候选
剪枝步: 利用频繁项集的反单调性对候选
统计支持度计数: 扫描数据库D, 对候选
为克服Apriori算法的缺陷, 韩家炜等提出了基于FP-tree的FP-Growth算法[7], 该算法只需对数据库进行两次扫描, 且不产生候选项集, FP-tree结构能对数据库进行有效压缩.
FP-tree中每个节点由4个域组成: 项标识item-name、节点计数item-count、节点链item-link和父节点指针item-parent. 同时为了方便对树进行操作, FP-tree还包含一个频繁项头表header-table, 它由两个域组成: 项标识item-name和项元链链头node-link, 其中node-link是指向FP-tree中具有相同项标识的首节点指针, FP-tree中实线是父节点指针, 虚线是节点链. FP-tree相关概念及结构细节见文献[1]. 使用表1中的示例数据生成的FP-tree如图1所示, 设最小支持度阈值
| 表 1 样例数据集 |

|
图 1 FP-tree结构 |
1.4 APFT算法
APFT算法[10]使用Apriori算法挖掘基于FP-tree的频繁模式, 该算法仍采用分治策略. APFT算法主要包括两个步骤, 第一步是利用FP-growth算法中构造树的方法构造FP-tree; 第二步是利用Apriori算法挖掘FP-tree. 在第二步中, 需要添加一个名为
算法1. APFT
Input: FP-tree, minsup
Output: all frequent patterns L
1) L=L1;
2) for each item
3)
4) return
Pseudocode
1) Find item p in the header table which has the same name with
2)
3) while q is not null
4) for each node qj!=root on the prefix path of q
5) if NTablehas a entry N such that N.Item-name=qj.item-name
6)
7) else
8) add an entry N to the
9)
10)
11)
12)
13)
14) repeat
15)
16)
17)
18) while q is not null
19) find prefix path
20)
21) for each
22)
23)
24)
25) until
26) return
为了提高基于FP-tree的Apriori算法的挖掘效率, 从进一步缩减数据库扫描次数以及增强算法的交互式挖掘与增量挖掘的方向改进. 首先, 将Apriori算法的apriori_gen()函数中的连接步进行优化. 由于连接步需要大量比较步骤, 并且会产生大量无用的候选项集, 因此增加了后续剪枝步和支持度计数步的时间开销. 其次, 将CP-tree[15]进行扩展, 提出了一个新的树结构ECP-tree(Extension of Compact Pattern tree). 由于在构造CP-tree的过程中包含所有项, 不论是频繁项还是非频繁项都参与了树的构造, 因此占用了大量的内存空间, 并且会影响频繁模式的挖掘效率. 在新构造的ECP-tree中只包含频繁项, 删除了非频繁项, 并且只经过一次数据库扫描就可以构造出一棵紧凑的前缀树, 新构造的树结构不仅支持交互式挖掘而且也支持增量挖掘.
2.2 优化连接步在给出优化思想之前, 首先了解两个关于集合的性质.
性质1. 包含k个不同项的k-项集有k个不同的(k–1)项子集;
性质2. 假设I为k-项集中的一个项, 根据性质1可得, 在k个子集中必有(k–1)个子集包含项I.
在Apriori算法的apriori_gen()函数的连接步中, 需要进行多次前(k–1)项的比较, 这大大增加了算法的时间开销. 经研究发现, 存在这样一个性质:
性质3. 假设
反证法: 假设包含项
根据性质3, 可对连接步进行优化, 在连接之前进行预处理, 删除不满足条件的
算法2. Pretreatment
Input: 频繁k-项集Fk
Output: 满足连接条件的频繁
1) for each items
2) for each item
3) if
4)
5) for each item
6) if
7) delete
8) return
为了说明优化流程, 用以下示例说明具体过程. 假设表2是事务数据库产生的所有频繁3-项集
| 表 2 所有频繁3-项集 |
在原始Apriori算法中, 保留所有频繁3-项集进入连接步, 连接产生的候选4-项集
| 表 3 所有候选4-项集 |
如表3所示, 表2中的12个频繁3-项集连接后共产生16个候选4-项集, 根据剪枝原理, 剪枝后剩下的候选4-项集只有{I2,I3,I4,I10}. 只有这一个候选4-项集进入支持度计数步. 连接步的预处理过程如下所示:
第一步: 计算表2中12个频繁3-项集中每一个项的计数, 结果如表4所示.
第二步: 由表4可知, 项I1、I5、I6、I7、I8、I9的计数小于k(即, 3), 因此对所有包含项I1、I5、I6、I7、I8、I9的频繁3-项集
| 表 4 频繁3-项集中每个项计数 |
| 表 5 预处理后的频繁3-项集 |
预处理后只剩4个频繁3-项集, 按照连接规则将这4个频繁项集进行连接, 生成一个候选4-项集{I2,I3,I4,I10}, 对这个候选项集进行剪枝操作, 没有被剪掉, 进入支持度计数步. 预处理后的结果与原始Apriori算法结果相同, 故预处理步骤是合理的.
2.3 新树的构造新树的构造主要包括两个阶段: 1)插入阶段; 2)重构阶段. 在插入阶段, 通过逐一扫描数据库中的事务项集, 根据项在事务中出现的先后顺序将它们插入树中. 由于将事务插入树中时, 它维护
本文对分支排序方法(BSM)进行了改进, 使该算法能够适应新提出的树结构. 在改进方法中, 如果路径没有按照新的排序顺序进行排序, 则将该路径删除, 并删除非频繁的项, 将剩余的频繁项按排序顺序排列到一个临时数组中, 最后再按顺序插入树中, 重复此过程最终将得到一棵紧凑的模式树. 改进的分支排序方法(IBSM, Improve Branch Sorting Method)的伪代码如算法3所示.
算法3. IBSM
Input: T和I
Output: 仅包含频繁项的Tsort和Isort
1) Compute Isort from I in frequency-descending order using merge sort technique
2) for each branch Bi in T
3) for each unprocessed path Pj in Bi
4) if Pj contains only frequent items in order according to Isort
5) Process_Branch(Pj)
6) else Sort_path(Pj)
7) Terminate when all the branches are sorted and output Tsort ang Isort.
8) Process_Branch(P){
9) for each branching node nb in P from the leafP node
10) for each sub-path from the leafk with k
11) if item ranks of all nodes betweennb and leafk are greater than that of nb
12) P=sub-path from nb to leafk
13) if P is contains only frequent items in order according to Isort
14) Process_Branch(P)
15) else P=path from the root to leafk
16) Sort_path(P)
17) }
18) Sort_ path(Q){
19) Reduce the count of all node of Q by the value of leafQcount
20) Delete all nodes contains infrequent items and sort remaining nodes in an array according to Isort order
21) Delete all nodes having count zero from Q
22) Insert sorted Q into T at the location from where it was taken
23)}
为了更好地理解改进树重构方法的工作原理, 使用表1给出的样例数据库进行详细说明, 设最小支持度阈值

|
图 2 插入阶段后的I和T |

|
图 3 重排I构造Isort |
新提出的树结构只需对数据库进行一次扫描, 就可以构造出一棵与FP-tree完全相同的树. 新的树结构支持交互式挖掘, 在交互式挖掘中, 用户可以为同一个数据库更改指定的最小支持度阈值. 在这种情况下, 我们可以在插入所有事务后保存树, 然后根据用户指定的最小支持度阈值重构树, 在

|
图 4 移除未排序路径 |

|
图 5 在临时数组中对路径排序 |
3 实验分析
为验证所提方法的有效性, 将改进方法运用到APFT算法中来挖掘频繁模式, 且与原始APFT算法、FP-Growth算法以及Apriori算法进行比较. 本文算法实验平台为: Intel Core i7-4790 CPU 3.6 GHz 处理器和8 GB内存, Windows 10 64位操作系统, 开发软件为Matlab R2014a. 实验所用的数据集有两个, mushroom数据库和T10I4D100K数据库, 均可从http://fimi.ua.ac.be/data/.下载, 数据集的特征如表6所示. 本文分别在这两种数据集上进行对比试验, 每组试验的参数都是不变的, 都是通过改变最小支持度阈值从而记录算法的运行时间, 算法运行的时间越小代表算法的挖掘速度越快.

|
图 6 将排序后的路径插入T中 |
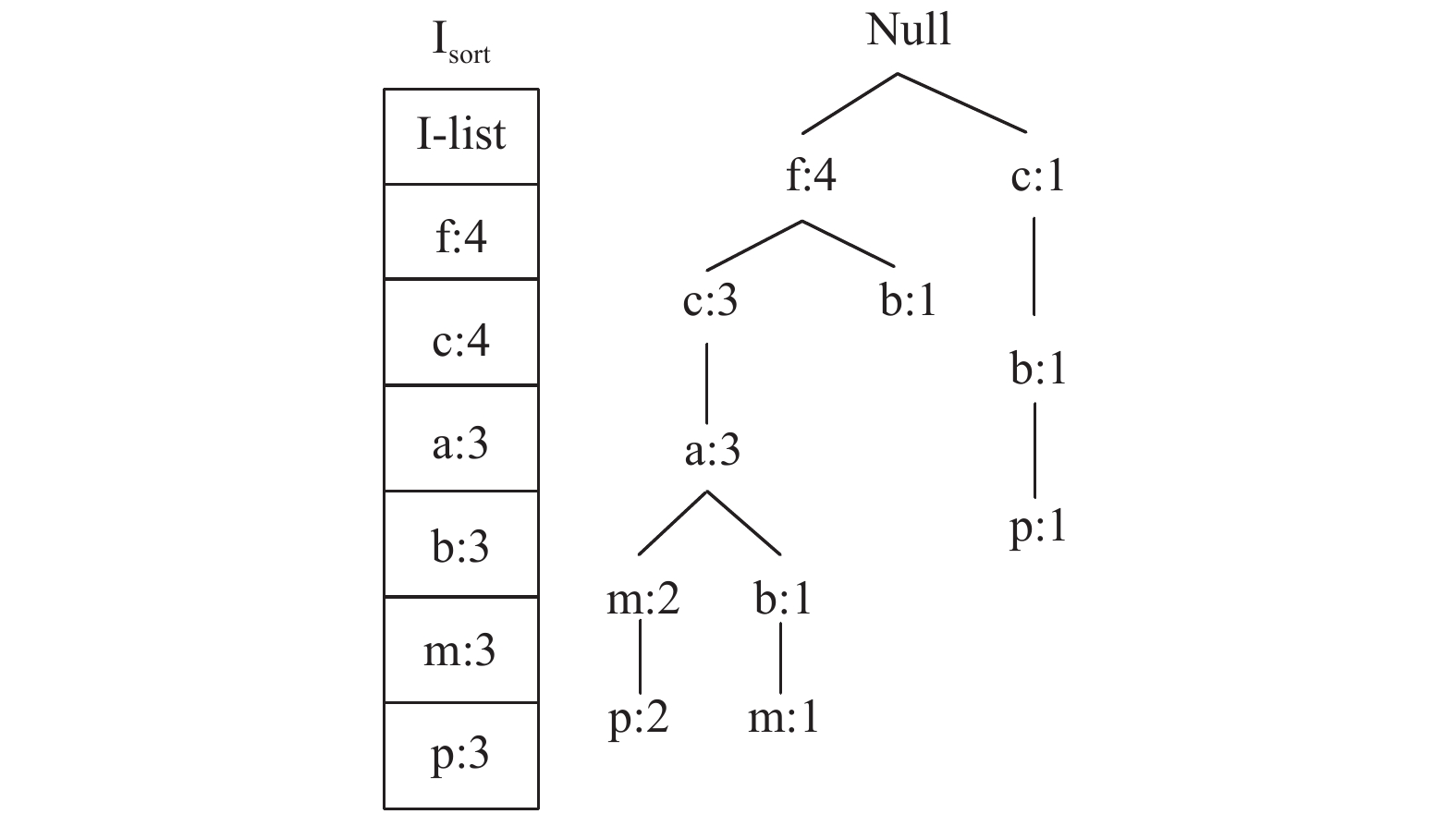
|
图 7 重构后的最终树 |
| 表 6 数据库特征 |
在相同条件下, 算法独立实验10次, 取其运行时间的均值作为算法最终结果. 两个数据集在不同算法和不同最小支持度阈值下的运行时间对比如表7和表8所示, 单位为秒(即, s). 从表中可以看出, 本文改进算法在运行时间上明显优于其他几个算法, 说明本文改进算法有效提高了频繁模式的挖掘速度. 从图8和图9中可以看出本文改进算法比原始APFT算法更高效, 主要原因有两个: 1)在算法的apriori_gen()函数前加入了连接预处理步骤, 对进入连接步的频繁k-项集进行剪枝, 减少了两两频繁项集前(k–1)项的比较次数, 因此减小了连接步的时间消耗, 并且候选项集的数量也减少了, 减小了剪枝步的时间开销; 2)新提出的树构只需对数据库进行一次扫描就可以构造出一颗紧凑的模式树, 虽然增加了树重构过程但这一过程基本上不会花费太多时间, 并且在挖掘过程中不需要额外的空间, 因此本文改进算法具有更好的空间可扩展性.
| 表 7 mushroom上不同算法运行时间对比 |
| 表 8 T10I4D100K上不同算法运行时间对比 |

|
图 8 mushroom上运行时间对比 |

|
图 9 T10I4D100K上运行时间对比 |
4 结束语
本文针对传统频繁模式挖掘算法存在的固有缺陷, 提出了一种基于APFT算法的改进频繁模式挖掘算法. 首先, 在算法的连接步前加入预处理过程, 对参与连接的频繁k-项集进行有效剪枝, 大大减少了连接步与剪枝步的时间开销; 其次, 对CP-tree进行扩展提出了一种新的树结构ECP-tree, 新的树结构是一棵紧凑的前缀模式树; 然后, 再将改进点与APFT算法结合用于频繁模式挖掘; 最后, 利用实验验证了改进算法的有效性.
为了有效对频繁模式进行挖掘, 本文将改进点与APFT算法结合, 由于新提出的连接预处理方法与紧凑树结构具有较好的可移植性, 因此改进点可与其它类似算法结合, 且并不影响挖掘效率, 相应地还能增强原始算法处理数据流问题的能力.
下一步的研究工作包括: 1)继续完善算法, 往并行计算方向扩展; 2)将该算法的思想扩展到最大、闭频繁模式的挖掘领域.
| [1] |
Han JW, Kamber M, Pei J. 数据挖掘: 概念与技术. 范明, 孟小峰, 译. 3版. 北京: 机械工业出版社, 2012.
|
| [2] |
Agrawal R, Imieliński T, Swami A. Mining association rules between sets of items in large databases. ACM SIGMOD Record, 1993, 22(2): 207-216. DOI:10.1145/170036 |
| [3] |
刘步中. 基于频繁项集挖掘算法的改进与研究. 计算机应用研究, 2012, 29(2): 475-477. DOI:10.3969/j.issn.1001-3695.2012.02.019 |
| [4] |
邢长征, 安维国, 王星. 垂直数据格式挖掘频繁项集算法的改进. 计算机工程与科学, 2017, 39(7): 1365-1370. DOI:10.3969/j.issn.1007-130X.2017.07.025 |
| [5] |
于守健, 周羿阳. 基于前缀项集的Apriori算法改进. 计算机应用与软件, 2017, 34(2): 290-294. DOI:10.3969/j.issn.1000-386x.2017.02.052 |
| [6] |
王蒙, 邹书蓉, 方睿. 一种基于矩阵的Apriori改进算法. 信息技术, 2018(3): 150-154. |
| [7] |
Han JW, Pei J, Yin YW. Mining frequent patterns without candidate generation. Proceedings of 2000 ACM SIGMOD International Conference on Management of Data. Dallas, Texas, USA. 2000. 1–12.
|
| [8] |
肖继海, 崔晓红, 陈俊杰. 基于COFI-Tree的N-最有兴趣项目集挖掘算法. 计算机技术与发展, 2012, 22(3): 99-102. DOI:10.3969/j.issn.1673-629X.2012.03.026 |
| [9] |
Yin M, Wang WJ, Liu Y, et al. An improvement of FP-Growth association rule mining algorithm based on adjacency table. MATEC Web of Conferences, 2018, 189(1): 10012. |
| [10] |
Lan QH, Zhang DF, Wu B. A new algorithm for frequent itemsets mining based on apriori and FP-tree. Proceedings of 2009 WRI Global Congress on Intelligent Systems. Xiamen, China. 2009. 360–364.
|
| [11] |
吴倩. 基于压缩FP-tree的频繁项集快速挖掘算法研究[硕士学位论文]. 上海: 华东理工大学, 2015.
|
| [12] |
张宁. 基于FP-tree的Apriori算法的改进. 信息通信, 2015(2): 94-95. DOI:10.3969/j.issn.1673-1131.2015.02.056 |
| [13] |
倪政君, 夏哲雷. 一种基于fp-tree的Apriori算法改进研究. 中国计量大学学报, 2018, 29(1): 50-54. DOI:10.3969/j.issn.2096-2835.2018.01.009 |
| [14] |
吴磊, 程良伦, 王涛. 基于事务映射区间求交的高效频繁模式挖掘算法. 计算机应用研究, 2019, 36(4). DOI:10.19734/j.issn.1001-3695.2017.10.0972. |
| [15] |
Tanbeer SK, Ahmed CF, Jeong BS, et al. Efficient single-pass frequent pattern mining using a prefix-tree. Information Sciences, 2009, 179(5): 559-583. DOI:10.1016/j.ins.2008.10.027 |
 2019, Vol. 28
2019, Vol. 28



