随着科技的进步, 极大的推动了气象行业的信息化建设, 气象数据的获取途径越来越多, 数据量急剧增长, 且其具有的空间复杂性、高维性、不稳定性, 使得传统的基于数值计算和统计分析的方法不能有效的处理, 在挖掘数据各要素之间的内部联系时更为乏力, 已经无法满足人类对高效准确气象服务的需求. 而数据挖掘算法和Hadoop等技术的出现, 为从海量气象数据中挖掘出潜在的规律和模式提供了新途径, 也为提高天气预报准确率, 做好灾害的提前预警提供了新思路[1].
目前, 已经有大量学者将数据挖掘算法应用到气象领域. 文献[2]将SVM方法应用于降水异常的分类预测中, 并利用四川盆地降水数据进行了实验, 结果表明所建立的模型在短期气候预测业务中有较好性能. 文献[3]采用Naïve Bayes算法对介休、运城、丰宁3个站进行了降水概率分级预报, 结果表明该方法可以通过降低数值模式空报率提高单站晴雨、小雨预报效果. 文献[4]选取湿度、温度、大气压、风速等要素为降水因子, 并采用决策树算法对降水进行预报, 实验结果表明改进后的模型有较好的适应性. 文献[5]采用改进的Adaboost算法集成反向传播(BP)神经网络组合分类模型, 通过构造多个神经网络分类器对江苏境内6个站点降水等级进行了预测, 结果表明所提出的模型有较好的预测精度. 但是这些模型所采用的都是较小的数据集, 不适用于较大规模的数据集. 随着气象预报精度、准度要求的提高, 传统的方法已经无法及时准确的处理海量数据.
本文针对以上不足, 采用Hadoop分布式系统处理海量数据, 同时考虑BP神经网络收敛速度慢, 容易陷入局部最小值的问题, 结合遗传算法全局搜索的优势对BP神经网络进行改进, 提出了在Hadoop平台上构建基于遗传神经网络算法的天气预报方法, 为海量气象数据挖掘提供了一个可行的方案.
1 遗传神经网络算法设计BP神经网络算法是大气科学领域的气候分析和气候预测中应用比较广泛的算法, 能够提供更好的预报能力[6–8]. 但BP神经网络算法收敛速度慢, 容易陷入局部最小值, 而遗传算法(Genetic Algorithm, GA)是一种全局优化的搜索迭代算法, 将其与BP神经网络结合, 可以克服BP神经网络的缺点, 加速网络的训练[9–10]. 本文首先利用GA算法优化BP神经网络的连接权和网络结构, 并得到一群全局性较好的个体, 在进一步利用BP神经网络得到最优解, 然后解码得到对应的BP神经网络连接权和网络结构, 最后输入检测样本进行降水等级的预测.
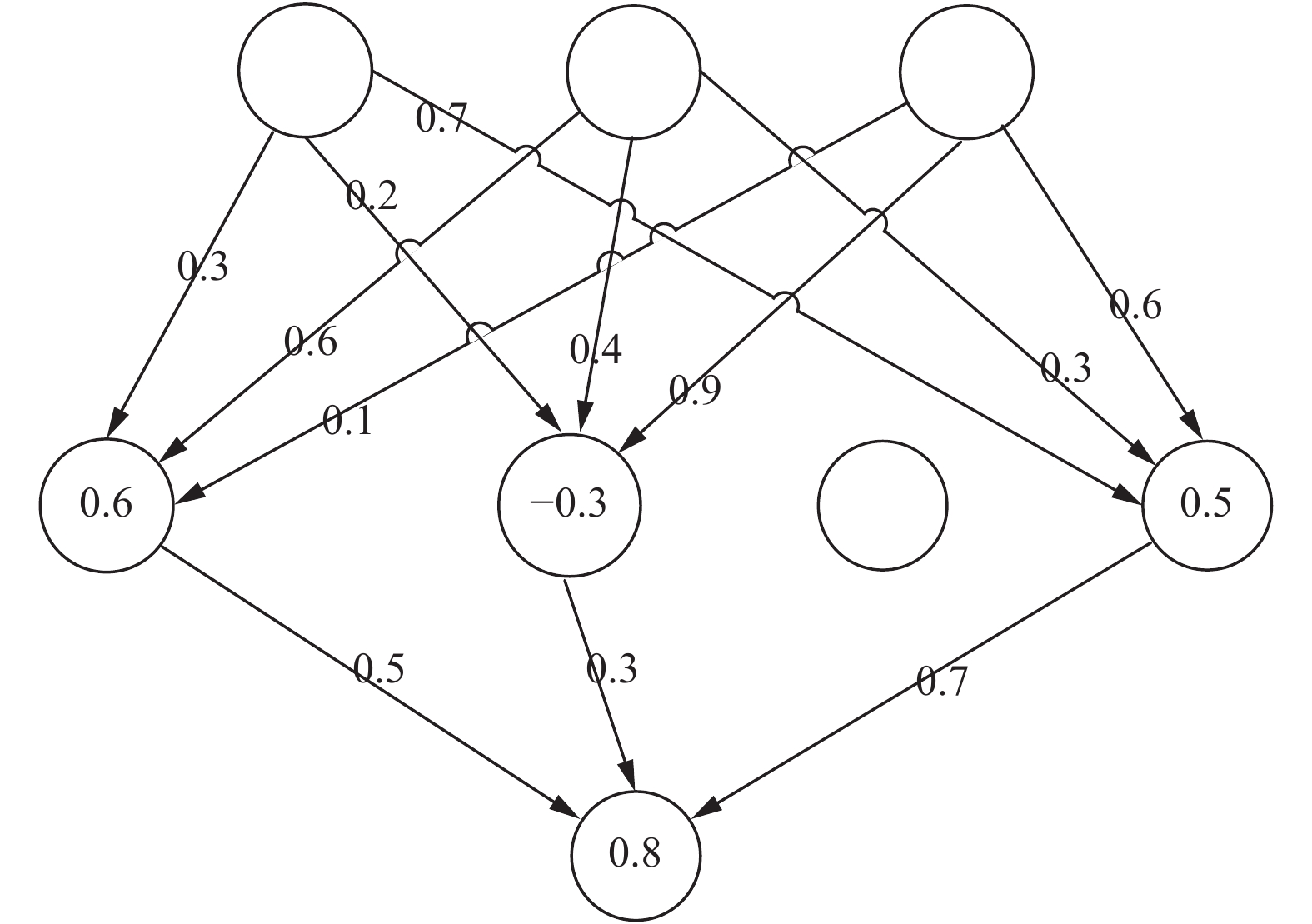
1.1 编码方式编码方式对算法的实现尤为重要, 不同编码方式决定了计算的复杂程度和网络学习的精度, 并且也影响到解空间的大小. 本文采用了实数编码, 另外对隐含层节点增加了一个二进制码用作控制基因, 以确定隐含层节点对输出层的影响关系, 具体编码方法举例如图1所示.
如图1, 隐含层第三个神经元没有连接, 即控制基因为: 1 1 0 1, 当为0时, 表示无连接, 1表示有连接. 神经元输入层到隐含层的权重系数矩阵, 按照一定顺序展开: 0.3, 0.2, 0.7, 0.6, 0.4, 0.3, 0.1, 0.9, 0.6. 隐含层神经元的阀值为: 0.6, –0.3, 0.5. 隐含层到输出层的权重系数为: 0.5, 0.3, 0.7. 输出层神经元的阀值为: 0.8. 整个神经网络的编码为: 1 1 0 1 0.3 0.2 0.7 0.6 0.4 0.3 0.1 0.9 0.6 0.6 –0.3 0.5 0.5 0.3 0.7 0.8.
|
图 1 编码示意图 |
染色体编码基因由控制基因、输入层到隐含层的权重系数、隐含层神经元的阀值、隐含层到输出层的权重系数以及输出层神经元的阀值依次组成, 共h+m*h1+h1+h1+n位(其中h为隐含层节点数, m为输入层节点数, h1为有效隐含层节点数,n为输出层节点数目).
1.2 初始种群的生成初始种群的生成, 本文采用随机数发生器随机生成初始种群.
1.3 适应度函数的建立假设输出层的实际输出结果为dj, 期望输出为yj, 则误差函数如下:
| ${{E}}\left( {{{w}},{{b}}} \right) = \frac{1}{2}\mathop \sum \limits_{j = 0}^{n - 1} {\left( {{y_j} - {d_j}} \right)^2}$ | (1) |
神经网络的目标是网络的期望输出与实际输出结果的误差函数值最小, 因此本文构造的适应度函数为:
| $f = \frac{1}{{{{E}}({{w}},{{b}})}}*{10^{ - 3}}$ | (2) |
选择策略是对当前群体不同适应度个体进行优胜劣汰的过程, 本文采用轮盘赌和最佳保留相结合的方法选择个体.
1.5 交叉算子(crossover operator)交叉算子是用根据选择操作得到的两个染色体个体, 以一定的概率Pc按照一定的方式互换一些基因, 从而得到子代染色体的过程. 交叉概率越大, 子代染色体更新的越快, 然而就更容易破坏优良个体. 交叉概率越小, 算法的收敛速度越慢, 通常Pc=0.5~1.0. 为了尽量不破坏适应度值高的染色体个体, 同时保证群体的多样性, 本文采用自适应的交叉率[11]公式如下:
| $\left\{ {\begin{array}{*{20}{l}} {{P_{c1}} - \dfrac{{\left( {{P_{c1}} - {P_{c2}}} \right)/\left( {{f_{\rm{max}}} - {f_{\rm{avg}}}} \right)}}{{{f_{\rm{max}}} - {f_{\rm{avg}}}}},f' > {f_{\rm{avg}}};}\\ {{P_{c1}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f' < {f_{\rm{avg}}}} \end{array}} \right.$ | (3) |
其中,
本文在进行交叉操作时, 把父代染色体对应基因位的染色体互换, 即控制基因位与对应的控制基因位互换, 权重系数基因位与对应的权重系数基因位互换, 阀值基因位与阀值基因位互换.
1.6 变异算子(mutation operator)变异操作是通过将染色体个体的编码基因中某些位用其它等位基因代替, 从而产生新的个体, 通常Pm=0.001~0.05. 本文采用自适应的变异率, 公式如下:
| $\left\{ {\begin{array}{*{20}{l}} {{P_{m1}} - \dfrac{{\left( {{P_{m1}} - {P_{m2}}} \right)/\left( {{f_{\rm{max}}} - {f_{\rm{avg}}}} \right)}}{{{f_{\rm{max}}} - {f_{\rm{avg}}}}},f' > {f_{\rm{avg}}};}\\ {{P_{m1}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f' < {f_{\rm{avg}}}} \end{array}} \right.$ | (4) |
其中,
以
| $X_j^{t + 1} = X_j^t + {c_j}$ | (5) |
其中,
本文设计的算法终止条件如下:
当算法运行到预先设定的最大的进化代数K0时, 就终止算法, 把得到的结果输出.
1.8 算法框架遗传神经网络算法具体步骤如下:
(1)确定解空间[12], 对解空间进行编码, 每串编码代表解空间的一个解.
(2)在编码的解空间中, 随机生成一个初始群体(不要求一定是可行解).
(3)对群体中的每一个个体进行适应度评价.
(4)根据个体的适应度, 对群体中的个体进行选择、交叉、变异遗传操作.
(5)生成新一代群体.
(6)反复进行(3)、(4)、(5), 每进行一次, 群体进化一代, 直至进化了K0代(K0为预置的进化代数).
(7)从第K0代群体中选择S可能具有全局性的进化解, 选择时要注意避免相似个体.
(8)分别以这些进化解为初始解, 用神经网络求解.
(9)比较S个由神经网络求得的解, 从而获得问题的最优解, 然后输入检测样本进行预测.
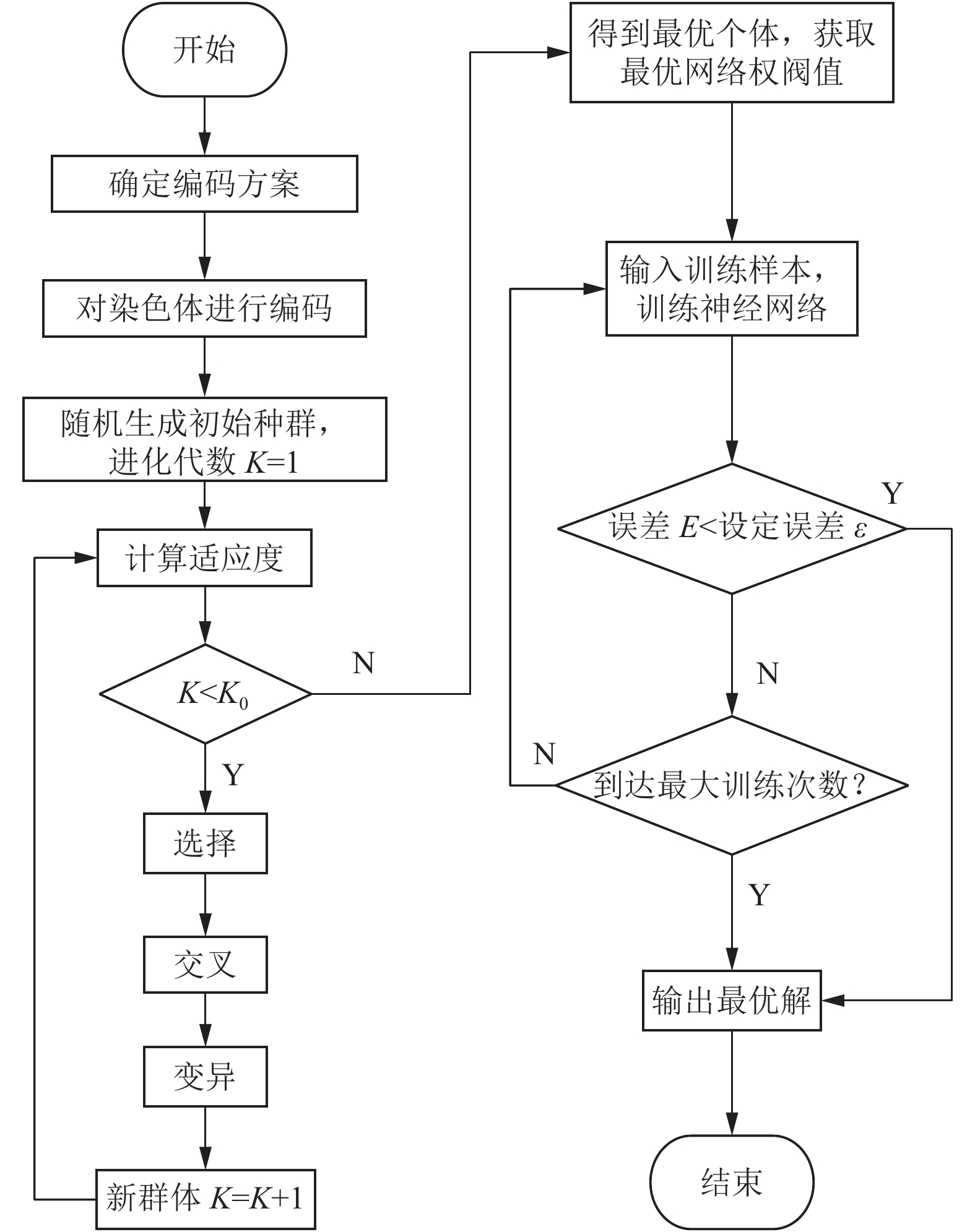
遗传神经网络算法流程图如图2所示.
|
图 2 遗传神经网络算法流程图 |
2 GA-BP算法的并行化
Hadoop下的MapReduce是Google公司提出的用于处理海量数据的分布式计算模型, 其主要由两个阶段组成: Map和Reduce. Map阶段主要负责将输入数据分为多个分片(split), 并将每个split交给一个Map Task, 最终转化为key/value数据结构. Reduce阶段将Map阶段的结果进行归约处理, 输出最终结果. 降水数据规模较大, 利用MapReuce分布式计算的优势, 可以快速的完成对海量气象数据的处理.
2.1 遗传算法的并行化GA算法的并行思想: 首先将整个群体分为m个种群, 然后每一个种群在对应的Map Task上独立完成种群的初始化、选择、交叉、变异等操作, 达到收敛条件后, 将Map得到的最后个体传递给相对应的Reduce Task, 然后将不同Reduce Task得到的个体适应度进行比较, 输出适应度值最大的个体.
Map函数伪代码如下:
Input: key, value
Output: key, best individual set
Public void map (writeable key, value){
InitPopulation();
EvaluateFitness();
Do{
Selection operator();
Crossover operator();
Mutation Operator();
}while (K<=K0)
OutputBestIndividual();}
Reduce函数伪代码如下:
Input: key, best individual set
Output: key, best individual
void reduce(individual, fitness)
{
CompareIndividualFitness();
Output();
}
遗传算法迭代完成后, 得到的结果就是BP神经网络的初始的权值和阀值.
2.2 BP神经网络的并行化神经网络算法的并行思想: 在Map阶段, 根据遗传算法输出的最优解得到神经网络的初始权值和阀值, 然后把训练样本转化为键值对作为输入, 对每个样本进行迭代运算, 计算误差, 并反向传播误差, 输出权值的改变量. 在Reduce阶段, 对Map输出的各个权值的改变量进行累加并求平均值, 对权值进行更新. 重复Map和Reduce阶段, 直到算法收敛.
Map函数伪代码如下:
Input: key, value
Output: key, weight change
Public void map (writeable key, value){
Do{
//For each sample
Error();
WeightChange();
}while (E<Ɛ)
OutputWeightchange();}
Reduce函数伪代码如下:
Input: key, weightchange
Output: key, mean weightchange
void reduce(key, weightchange){
Do{
SumWeightchange();
MeanWeightchange();
}while()
Output();}
3 实验结果及分析 3.1 实验环境实验采用Hadoop分布式集群[13], 选取1台虚拟机作为NameNode节点和JobTracker服务节点, 负责管理分布式数据和分解任务的执行, 其它7台虚拟机作为DataNode和TaskTracker服务节点, 负责分布式存储和任务执行. 虚拟机各项配置及集群的配置信息分别如表1、表2所示.
| 表 1 虚拟机配置信息表 |
| 表 2 集群信息配置 |
由表2我们可以看出Hadoop分布式集群在运行时需要一系列的后台程序, 主要有:
NameNode-负责管理文件系统的Namespace.
DataNode-负责管理各个存储节点.
SecondaryNameNode-NameNode的热备, 负责周期性的合并Namespace image和Edit log.
ResourceManager-负责调度资源.
NodeManager-负责管理slave节点的资源.
3.2 实验数据及预处理实验采用的数据来自于天津市地面气候资料日值数据集, 该数据集以天津市13个站1951年~2006年各月的A0、D、A文件为数据源, 通过统计软件处理转换成日平均气压、日最高气压、日最低气压等气象要素日值资料, 如表3所示.
| 表 3 天津市地面气候资料日值数据集表 |
按照中国气象局的划分, 将20-20时降水量划分为7类, 如表4所示, 实验中不考虑31XXX降雪以及32XXX雾露霜天气.为使网络有良好的收敛性和映射能力, 消除原始数据形式不同所带来的不利, 通常的做法是归一化处理, 将原始目标、输入数据转换到区间内将数据归一化到[0, 1]之间. 归一化公式如下:
| ${x_i} = \frac{{{x_i} - {x_{\rm{min}}}}}{{{x_{\rm{max}}} - {x_{\rm{min}}}}}$ | (6) |
其中,
| 表 4 降水量等级分类标准 |
在实验中, 1951年~2005年的数据作为训练数据, 2006年的数据作为检测数据. 经过数据预处理后13个台站共计214 706个样, 如表5所示.
| 表 5 站点数据表 |
总体样本降水等级分布如图3所示, 从图3中不难看出13个台站无雨的样本数最多, 达到了80.32%, 特大暴雨的样本数最少, 约1.85%.
3.3 降水因子选择天津市地面气候资料日值数据集共包含了27个要素, 去除降水量还有24个要素, 而预测因子的选择很大程度上影响了预测的结果, 本文利用Pearson[14]相关系数法来考察各要素对降雨量的影响力, 公式如下:
| ${\rm{r}} = {r_{xy}}\frac{{\displaystyle\mathop \sum \nolimits_{i = 1}^n ({x_i} - \overline x )({y_i} - \overline y )}}{{\sqrt {\displaystyle\mathop \sum \nolimits_{i = 1}^n {{({x_i} - \overline x )}^2}} \sqrt {\displaystyle\mathop \sum \nolimits_{i = 1}^n {{({y_i} - \overline y )}^2}} }}$ | (7) |
其中, x与y分别为2个变量的观测值.

|
图 3 总体样本降水等级分布图 |
若r>0, 表示2个变量是正相关的; 若r<0, 则表示2个变量是负相关,n为样本数量(本文选100个样本计算相关系数). 其它要素与降雨量之间的相关性初步由Pearson求出之后, 还要经过显著性检验再最后判断. 显著性检验公式为:
| ${\rm{t}} = \frac{{|{r_{xy}}|}}{{\sqrt {(1 - r_{xy}^2)/(n - 2)} }}$ | (8) |
分别计算平均气温、日最低气温、平均水汽压等要素与降雨量的相关系数, 如表6所示.
| 表 6 各要素与降雨量之间的相关系数 |
表6中平均相对湿度、小型蒸发量及大型蒸发量与降雨量的相关性已通过0.01显著性检验, 平均水气压、最小相对湿度、平均本站气压、日最高本站气压、日最低本站气压与降雨量的相关性已通过0.05显著性检验, 最后结合气象专家的意见, 选取了平均气温、日最低气温、平均水汽压、平均相对湿度、最小相对湿度、平均风速、最大风速、最大风速的风向、极大风速、极大风速的风向、日照时数这11个要素作为预测因子. 网络结构为11-h-7三层网络, 其中11为输入层的节点数目, 即11个预测因子作为网络的输入向量, h为隐含层的数目,
对13个站06年降水等级预测结果如表7所示, 由表7可以看出, 本文提出的算法对整体样本降水等级的预测准确度较高, 达到了82.4%.
| 表 7 06年降水等级预测结果 |
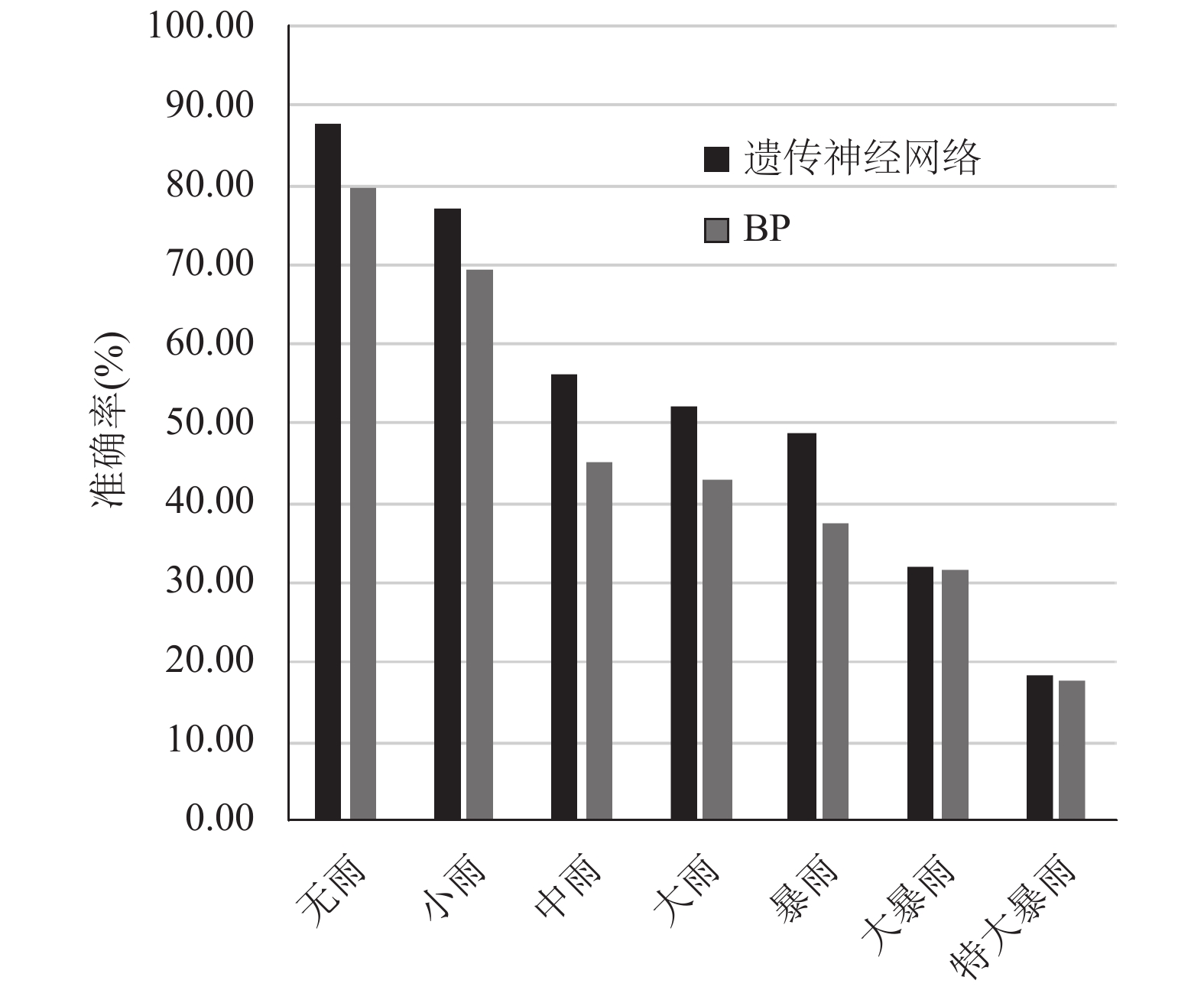
与传统的BP算法对比实验结果如图4所示, 从图中可以看出本文提出的遗传神经网络算法对所有降水等级的预测准确率都要优于传统的BP神经网络算法, 对无雨的预测准确度最高, 约87%, 而对特大暴雨的预测准确度最低, 一方面是因为实验样本中无雨的样本数量占总样本数的80.32%, 远大于其它降水等级的样本数, 所建立的模型更准确, 而特大暴雨样本数量仅占总样本数的1.85%, 对模型的训练不充分, 另一方面是因为特大暴雨的成因很复杂, 我们实验仅仅选取了众多因子中相关性较高的11个因子, 这是远远不够的, 实际情况要复杂的多, 需要结合各种方法综合预测才行.
为了检测所提出方法的扩展性和高效性, 分别在不同的节点数进行了实验, 运行时间结果如图5所示, 由图5我们不难看出, 随着DataNode节点数量的增加, 算法的运行时间明显缩短, 说明本文提出的方法在Hadoop平台上有很高的运行效率和扩展性.
|
图 4 实验结果对比图 |

|
图 5 不同节点运行时间图 |
4 结论与展望
本文基于Hadoop大数据离线分析平台构建了基于遗传神经网络算法的天气预报方法, 并以天津市13个台站1951~2006年的地面气候资料日值数据为基础, 建立了遗传神经网络预测模型, 最后以降雨量等级为决策属性进行了实验. 结果表明:
1)本文提出的方法对降水等级的预测准确率优于传统的BP算法, 整体预测准确率达到82.4%, 其中对于等级R0的预测精度最高, 高达87%.
2)该方法可以有效的处理海量气象数据, 同时具有很高的运行效率和良好的扩展性, 为天气预报提拱了一种全新的思路和方法.
本文的方法对降水因子仅考虑了相关性比较高的11个因子, 对特大暴雨预测准确率很低, 还有一些方面需要进一步研究, 比如可以结合T213数值天气预报, 筛选出一些非常规的气象要素来进行降水等级的预测, 以及寻找更有效的算法来解决这个问题, 这些方面都很有意义, 值得在未来的研究中仔细钻研.
| [1] |
李海涛, 刘云生, 兰长杰. 基于Hadoop的生物质能源工程数据资源管理平台. 计算机系统应用, 2018, 27(5): 80-85. DOI:10.15888/j.cnki.csa.006341 |
| [2] |
杨淑群, 芮景析, 冯汉中. 支持向量机(SVM)方法在降水分类预测中的应用. 西南农业大学学报(自然科学版), 2006, 28(2): 252-257. DOI:10.3969/j.issn.1673-9868.2006.02.020 |
| [3] |
胡邦辉, 刘善亮, 席岩, 等. 一种Bayes降水概率预报的最优子集算法. 应用气象学报, 2015, 26(2): 185-192. DOI:10.11898/1001-7313.20150206 |
| [4] |
Prasad N, Kumar P, Mm N. An approach to prediction of precipitation using gini index in SLIQ decision tree. Proceedings of the 4th International Conference on Intelligent Systems, Modelling and Simulation. Bangkok, Thailand. 2013. 56–60.
|
| [5] |
王军, 费凯, 程勇. 基于改进的Adaboost-BP模型在降水中的预测. 计算机应用, 2017, 37(9): 2689-2693. DOI:10.11772/j.issn.1001-9081.2017.09.2689 |
| [6] |
Wu JS, Long J, Liu MZ. Evolving RBF neural networks for rainfall prediction using hybrid particle swarm optimization and genetic algorithm. Neurocomputing, 2015, 148: 136-142. DOI:10.1016/j.neucom.2012.10.043 |
| [7] |
胡健伟, 周玉良, 金菊良. BP神经网络洪水预报模型在洪水预报系统中的应用. 水文, 2015, 35(1): 20-25. DOI:10.3969/j.issn.1674-9405.2015.01.005 |
| [8] |
赵正佳, 黄洪钟, 陈新. 优化设计求解的遗传-神经网络新算法研究. 西南交通大学学报, 2000, 35(1): 65-68. DOI:10.3969/j.issn.0258-2724.2000.01.016 |
| [9] |
郭强, 朱若函, 张晓萌. 基于遗传禁忌算法优化的模糊神经网络垂直切换算法. 计算机应用研究, 2016, 33(3): 840-842, 847. DOI:10.3969/j.issn.1001-3695.2016.03.045 |
| [10] |
谢建宏. 基于并行量子遗传神经网络的自诊断智能结构传感器的优化配置. 计算机应用研究, 2012, 29(3): 919-922. DOI:10.3969/j.issn.1001-3695.2012.03.033 |
| [11] |
Jajodia S, Samarati P, Sapino ML, et al. Flexible support for multiple access control policies. ACM Transactions on Database Systems, 2001, 26(2): 214-260. DOI:10.1145/383891.383894 |
| [12] |
金龙, 吴建生, 林开平, 等. 基于遗传算法的神经网络短期气候预测模型. 高原气象, 2005, 24(6): 981-987. DOI:10.3321/j.issn:1000-0534.2005.06.019 |
| [13] |
宋连春, 肖风劲, 李威. 我国现代化气候业务现状及未来发展. 应用气象学报, 2013, 24(5): 513-520. DOI:10.3969/j.issn.1001-7313.2013.05.001 |
| [14] |
殷长春, 孙思源, 高秀鹤, 等. 基于局部相关性约束的三维大地电磁数据和重力数据的联合反演. 地球物理学报, 2018, 61(1): 358-367. DOI:10.6038/cjg2018K0765 |
| [15] |
陈闯, Chellali R, 邢尹. 改进遗传算法优化BP神经网络的语音情感识别. 计算机应用研究, 2019, 36(2): 344-346, 361. |
 2019, Vol. 28
2019, Vol. 28


