近年来, 深度学习[1]作为机器学习的分支, 在多个领域均取得了较大的进展. 而卷积神经网络(Convolutional Neural Network, CNN) 作为深度学习的代表算法之一, 其在计算机视觉[2]、自然语言处理[3]等领域有着显著的成果.
因为在深度学习的应用的效果提升的同时, 其网络结构也变得越来越复杂, 使得深度学习对计算资源的要求也越来越高, 传统的计算资源已经不能满足其计算量大的需求. 如在传统的CPU架构 (X86和ARM), 其主要是基于通用的计算而发展应用的, 其基本操作为算术操作和逻辑操作, 而在深度学习的处理中, 单个神经元的处理往往需要成百上千的指令才能完成, 因此其对深度学习的处理效率很低. 如谷歌使用上万个X86的CPU核运行7天来训练识别一个猫脸的深度学习神经网络[4]. 因此, 基于深度学习的加速器的设计应运而生. 在设计加速器的阶段, 除了需要考虑深度学习算法本身的优化外, 还需要考虑如何提高计算资源的利用率, 以提高加速器的性能. 例如中科院设计的DianNao[5], 该架构注重对数据并行方面的优化, 使用三级的流水结构, 使用输入输出队列来保持激活层计算和权重计算参数, 输入的数据根据队列的大小进行分块. 同时因为数据的输入是按块输入的, 得到的输出并非最后的结果, 为了避免数据的重复存取, 其结构中设计寄存器来临时存储, 以减少数据的传输. Dally WJ团队设计的SCNN[6]硬件架构由多个PE组成, 基于7层嵌套的卷积计算算法,并对该循环进行并行加速. 其采用对卷积的激活和权重计算进行分块处理, 首先对权重计算进行分组, 将通道数进行切分到多个PE上, 每个PE上得到部分的输出. 同时基于该输出再对激活层运算进行分块处理, 将计算后的输出以广播的形式广播到每个PE, 来完成乘累加运算. 本文主要考虑CNN的每层计算任务的数据分布特点, 结合BWDSP的众核架构的设计, 对计算任务的划分进行设计, 以此减少其数据的传输量, 从而提升其加速器的效率.
本文的主要工作如下: 基于计算任务的特点, 设计合理计算任务划分的策略. 并基于VGGNet-16网络模型, 测试其优化前后数据的传输量. 本文余下内容由以下部分组成: 第1部分介绍了CNN的结构和BWDSP的众核架构; 第2部分介绍了在众核BWDSP架构下, 将数据并行与卷积计算特点结合设计的数据划分策略; 第3部分展示了本文提出的优化方法在VGGNet-16网络模型的测试实验; 第4部分是总结与展望.
1 CNN网络模型与BWDSP众核架构 1.1 CNN网络模型CNN是一种前馈神经网络 (feed neural networks), 其包含输入层、隐藏层、输出层. 其中隐藏层主要由卷积层、池化层和全连接层三类层次组成. 在较为复杂的CNN模型中, 隐藏层可能会包含多段卷积和池化层. 其中卷积层主要用来实现对输入的数据的特征的提取, 池化层主要是对特征进行选择和信息过滤, 而全连接层一般是作为隐藏层的最后一部分, 并将所包含的信息传递给下一层全连接层. 如图1显示的是较为简单的CNN模型-LeNet5[7], 其是LeCun Y设计用于手写数字识别的卷积神经网络, 具有2个卷积层, 2个池化层和2个全连接层.
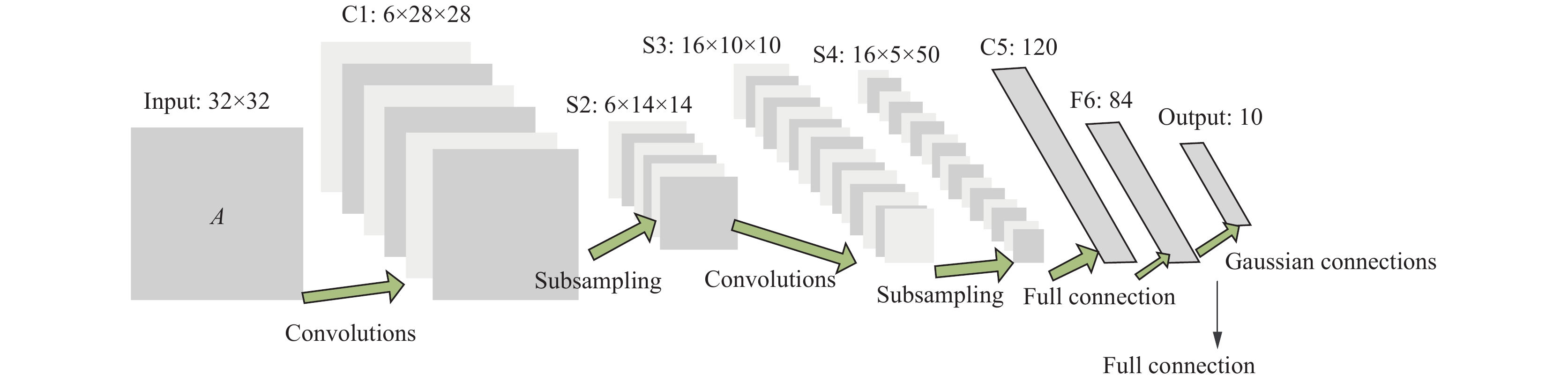
|
图 1 LeNet5网络结构图 |
1.2 BWDSP的众核架构
本文的单核计算单元是由中国电子科技公司第三十八所研制的BWDSP系列处理器, 可广泛应用于各种高性能领域.
BWDSP系列处理器基于分簇式架构, 其指令系统支持VLIW和SIMD类型的操作. 每个处理器上有4个簇, 每个簇上有4个支持MAC操作的乘法器, 其最高可达30 GOPS的运算能力. 其体系结构和计算能力适合处理大数据量和大计算量的深度学习任务. 如图2为BWDSP[8]体系结构图.
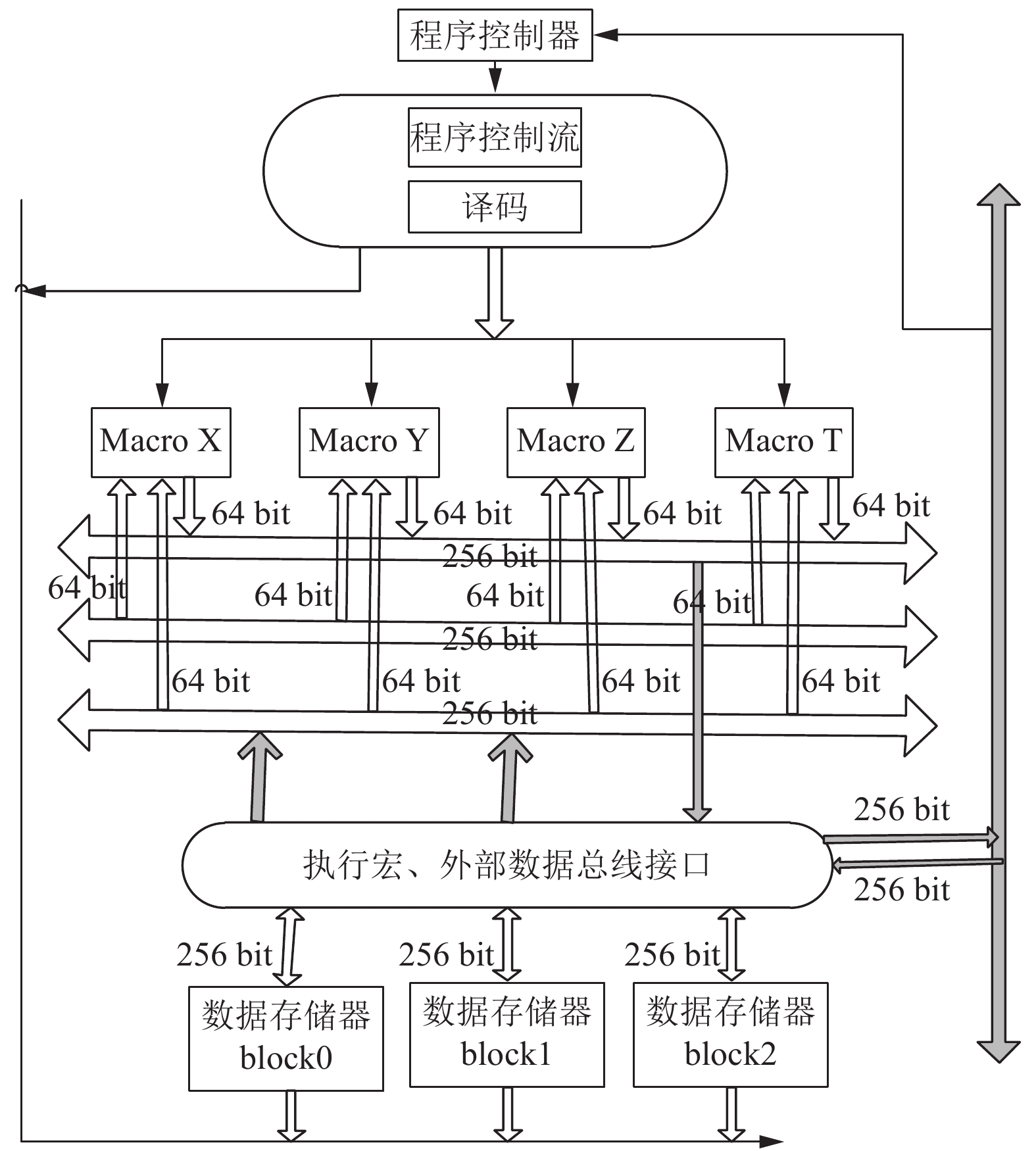
|
图 2 BWDSP体系结构 |
本文主要基于BWDSP的众核架构[9]及该架构所设计的众核计算算法[9]进调度任务的划分及其优化, 其架构如图3所示. 该架构由56个计算核心组成, 其主要考虑到主流的CNN网络, 如VGG, ResNet[10]等, 其卷积层的输入的高和宽的大小都是7的倍数, 故采用56个核心的框架结构, 能够保证大部分的卷积层在进行数据任务的划分时, 可以比较均衡的划分到计算核上, 使得计算核负载比较均衡. 同时, 架构中每个计算核心由三个buffer区组成, 每个buffer设置了连接计算核与片上互连的两个端口, 且设置为同步的. 该架构通过设计多缓冲区的方式来实现数据的传输和计算并行的进行, 并采用轮转三缓冲区的形式来降低片上内存的需求. 其轮转缓冲区的工作方式是: 采用三缓冲区方式来存储中间计算的结果, 三个缓冲区轮流作为输入缓冲区、输出缓冲区和进行下一次计算输入的数据传输的缓冲区.
BWDSP众核架构的计算算法是把单个输出的计算任务分配给单独的核进行计算, 且与输出相关的计算所有的输入加载到计算核的局部内存中. 在单个计算核完成其计算时, 将该核的局部内存的数据输出给其他核, 当所有的核传输完时, 即下一层的输入准备完备后, 开始进行下一层的计算.
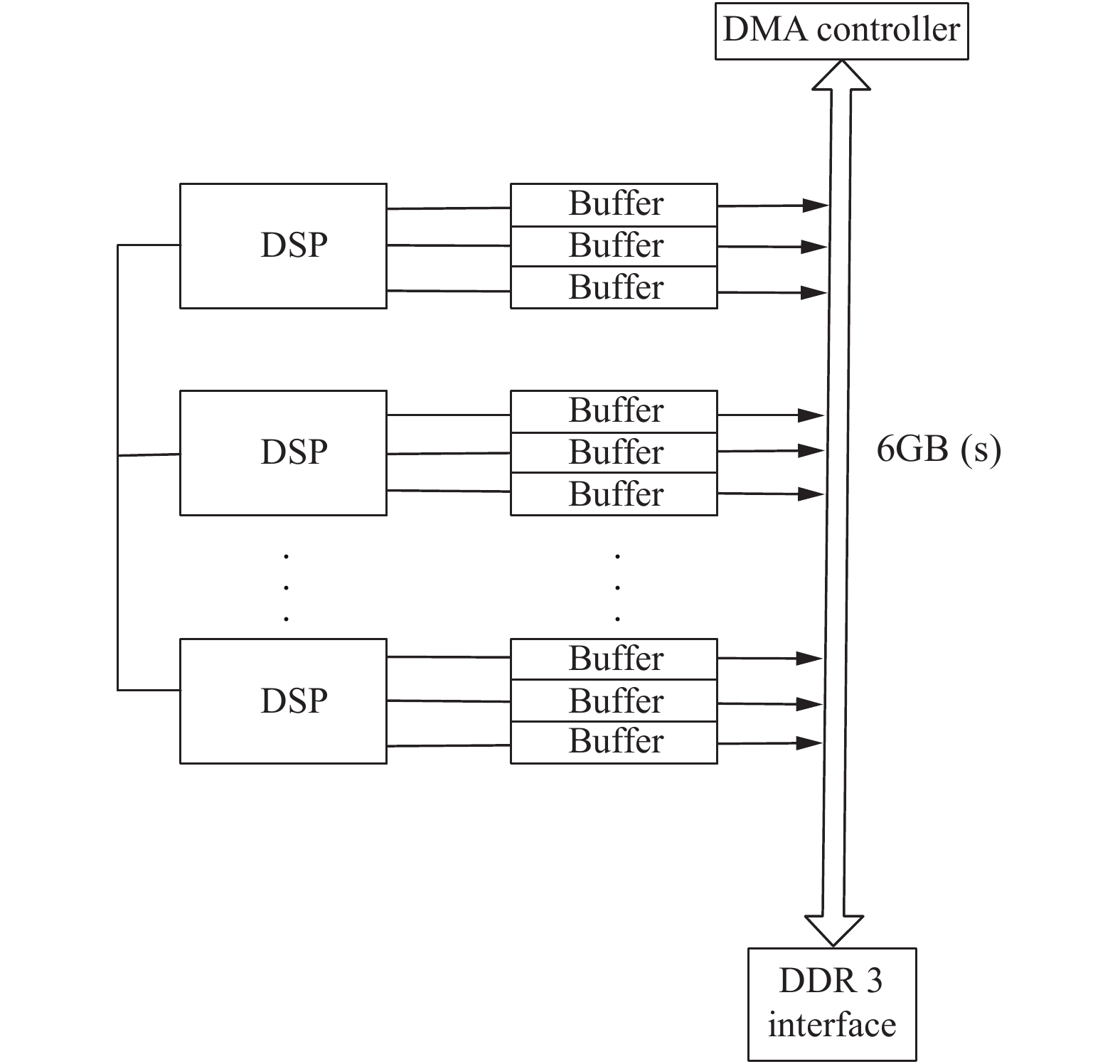
|
图 3 BWDSP众核架构 |
2 计算任务的划分设计
基于BWDSP众核架构和计算算法的设计, 本文设计的计算任务划分设计如图4所示. 因为现有的深度学习框架, 如TensorFlow[11], Caffe[12]等, CNN网络模型均以图的形来定义. 本文也采用了该方案, 即将CNN网络模型定义为有向无环图Graph, 此时CNN网络的输入输出数据等均以图的节点的形式保存, 然后使用Graph Optimizer定义的有向无环图Graph进行优化处理, 通常采用层融合的方式进行优化, 即将卷积操作、激活操作和池化操作进行融合处理, 将三个操作计算融合为为一个操作进行计算. 接着优化后的图模型的节点通过Layer Partition并依据计算核的众核计算算法来对数据的输出进行划分分配, 得到每个核的需要计算的输出数据; 然后Route Generator根据每个计算核的输出数据来反向推出输入的数据, 以此来完成众核间的数据交换并生成路由信息. 最后通过Execution生成执行计划交于计算核去执行.
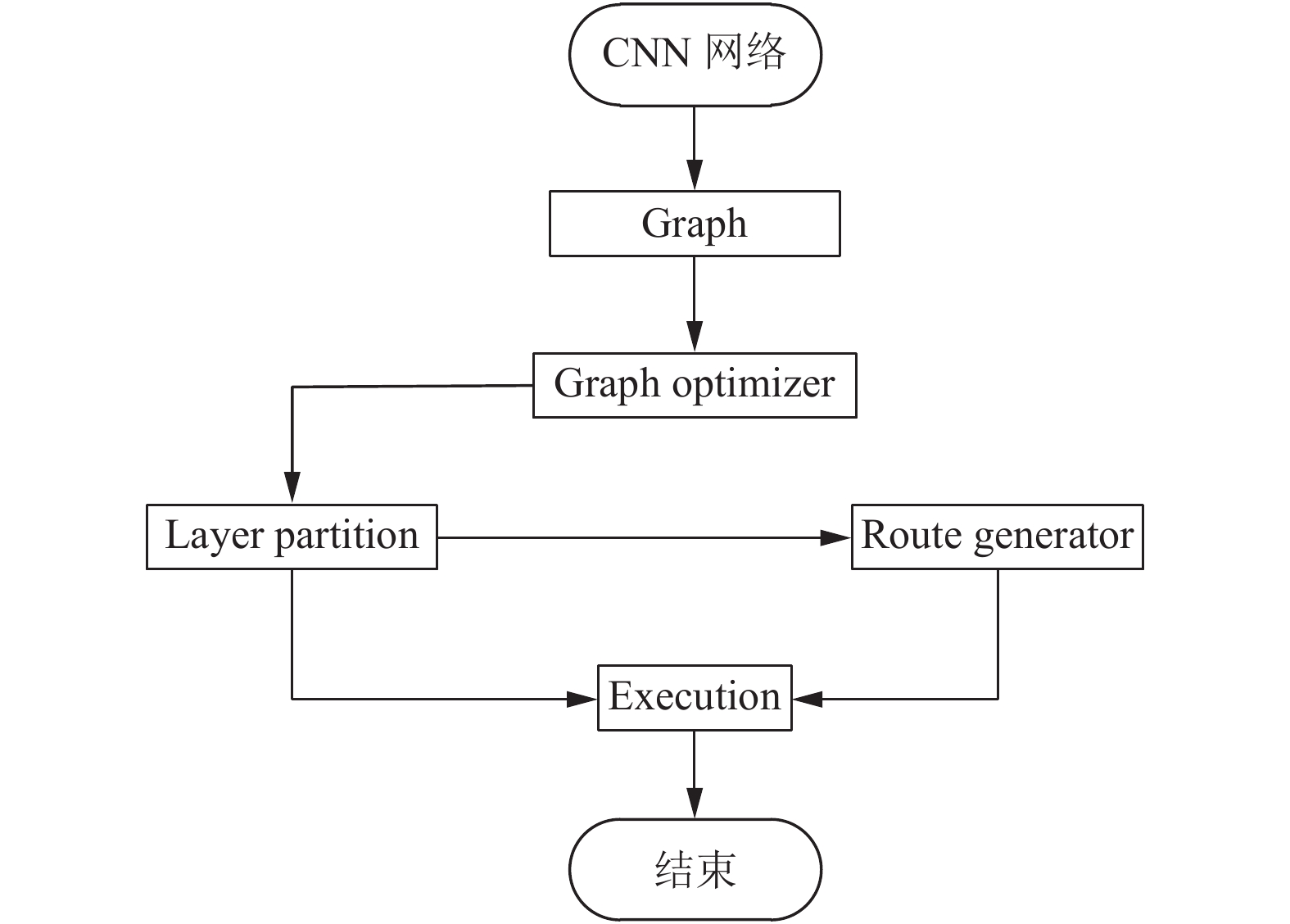
|
图 4 划分策略流程 |
在卷积神经网络中, 每次进行卷积计算后, 输出的数据尺寸会有所缩小, 同时原始图片的边缘部分像素点在输出中采用的较少, 其输出的数据信息会丢失到边缘位置的很多信息, 当网络的层数越深时, 所丢失的边缘位置的数据就越多, 到最后可能无数据信息可用. 因此, 卷积计算采用了填充操作. 一般地, 卷积神经网络采用两种填充方式: 填充和不填充, 分别为“SAME”和“VALID”. 其中, “SAME”方式为数据填充操作, 即对原始的输入数据进行区域补零操作, 其对输入的原始数据在高度和宽度上进行数据填充, 改变了输入数据的尺寸大小, 使得卷积计算后的输出数据的尺寸与计算前的原始输入数据的尺寸相同; “VALID”方式为数据的不填充操作, 即不会改变原始的数据的输入. 两种方式所对应不同的输入数据和输出数据的高和宽的大小关系如下所示. 式(1)为“SAME”方式, 式(2)为“VALID”方式, 具体的参数的含义如表1所示.
| 表 1 计算任务划分参数 |
| $\left\{ \begin{aligned} & {O_H} = \left\lceil {\dfrac{{{I_H}}}{{{F_H}}}} \right\rceil \\ & {O_W} = \left\lceil {\dfrac{{{I_W}}}{{{F_W}}}} \right\rceil \end{aligned} \right.$ | (1) |
| $\left\{ {\begin{split} & {{O_H} = \left\lceil {\dfrac{{{I_H}{\rm{ - }}{F_H} + 1}}{{{F_H}}}} \right\rceil } \\ & {{O_W} = \left\lceil {\dfrac{{{I_W} - {F_W} + 1}}{{{F_W}}}} \right\rceil } \end{split}} \right.$ | (2) |
数据并行(data parallel)计算[13]由hillis提出, 即指的在计算过程中同时对大量数据进行相同或者类似的操作. 该方法是基于负载均衡的划分方式, 但是并未考虑到CNN网络的模型特点, 即只是简单的将数据进行均等的切分到各个计算核上进行计算. 因此, 每个计算核需要计算的输入数据在高度和宽度维度上对应尺寸如式(3)所示.
| $\left\{ {\begin{aligned} & {AV{G_H} = \left\lceil {\frac{{{I_H}}}{N}} \right\rceil } \\ & {AV{G_W} = \left\lceil {{I_W}} \right\rceil } \end{aligned}} \right.$ | (3) |
该方法在对于大数据量的问题时, 可以采用其进行高效的处理. 但是在卷积计算中, 除了具有数据量大的特点, 还具有其填充和数据重叠等特性. 因此本文在考虑数据并行的同时将与卷积计算的特性结合起来, 可以进一步减少数据传输.
2.2 卷积任务的并行化划分设计在CNN网络模型的卷积计算过程中, 会涉及到填充和数据的重叠部分的操作. 本文在众核BWDSP架构下, 结合其特点并与数据的并行性在设计了计算任务的划分方法, 并与并行处理方法.
因为在进行卷积计算时会涉及到填充和数据重叠等操作, 因此当采用数据并行的方法对计算任务进行划分时, 核间还会涉及到大量的数据交换. 为了防止该情况的出现, 卷积层的数据划分策略以输出数据来进行, 即以输出数据的尺寸考虑出发, 反向推出输入的数据的尺寸, 然后将该种尺寸的数据交于计算核去计算.
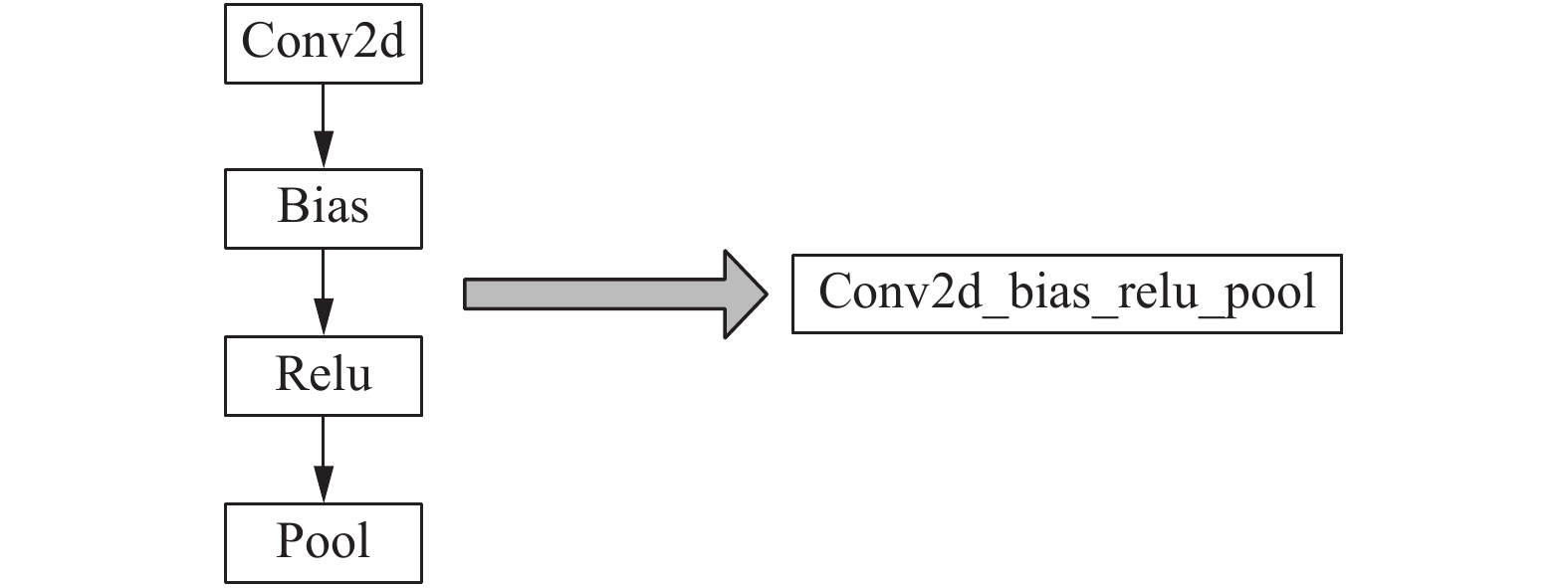
一般卷积在进行计算时, 卷积操作后一般直接是激活操作, 接着是池化层的操作, 本文先对计算任务进行图优化处理, 即进行卷积层计算的融合操作, 将多个操作融合为一个操作计算. 如图5所示. 此时在进行卷积计算后, 可以直接在本地实现激活操作和池化层的操作的计算, 以减少数据量的传输.
优化的数据划分根据CNN网络模型的计算特点, 针对卷积层、池化层的数据分布和计算特点采用了两种不同的划分策略. 一般地, 池化层和卷积层的划分策略相同, 如式(4)所示. 但是当网络结构进一步加深时, 其数据的尺寸会变得越来越小, 当OH<2×N时, 就会存在AVGH为1的情况. 而在池化层一般会采用2×2尺寸大小的池化操作, 此时采用式(4)进行池化层的计算时需要进行核间的数据交换, 因此需要将整行的数据分为两个部分, 即更细粒度的划分, 如式(5)所示, 该方可以有效的减少数据的传输.
|
图 5 卷积层融合 |
| $\left\{ {\begin{aligned} & {AV{G_H} = \left\lceil {\dfrac{{\frac{{{O_H}}}{N} - 1}}{{{S_H}}} + {F_H}} \right\rceil } \\ & {AV{G_W} = \left\lceil {\dfrac{{{O_W} - 1}}{{{S_W}}} + {F_W}} \right\rceil } \end{aligned}} \right.$ | (4) |
| $\left\{ {\begin{aligned} & {AV{G_H} = 4} \\ & {AV{G_W} = \left\lceil {\frac{{\frac{{{O_H} \times {O_W}}}{{2 \times N}} - 1}}{{{S_W}}} + {F_W}} \right\rceil } \end{aligned}} \right.$ | (5) |
在式(4)中对数据的划分, 考虑了计算任务的填充操作, 并对输出的数据进行划分, 该方式在卷积计算完成后可以直接进行数据的激活和池化操作. 但是当数据的尺寸较小时, 存在一种情况, 即单个计算核只计算一行数据时, 但因为池化计算时一般采用2×2的尺寸的数据, 此时式(4)不能满足无数据的传输. 因此在这种情况下, 采用式(5)进行划分, 即在高度和宽度的方向上均进行划分操作, 此时在计算池化层不需要再进行传输. 故为了更好地减少数据传输, 卷积计算任务的划分采用两者相结合的方式.
综上, 对计算任务的划分方式的分析和区别如表2所示.
| 表 2 数据划分方式对比 |
3 实验分析 3.1 实验数据
为了验证该划分策略的有效性, 本文以经典的卷积神经网络模型VGGNet-16[14]为实验数据, 该模型曾取得了ILSVRC2014比赛分类项目的第2名和定位项目的第1名, 其网络结构参数如表3所示.
实验中按照两种不同的数据划分方式对卷积网络层的数据进行划分, 如表4所示网络层的部分数据划分数据, 其数据格式为 (高度开始∶高度结束, 宽度开始∶宽度结束). 表4中在conv1_2和conv2_2中的数据划分中, 基于一般的和优化的数据划分方法, 每个核分配的计算数据量的差别主要在高度的差别, 宽度基本一致. 因为此时的数据的高度在计算完成后的大小尺寸可以满足池化层输入的数据的尺寸的要求, 即池化层的尺寸大多为2×2的大小, 即满足偶数倍的要求, 故可以在卷积计算之后直接进行池化计算, 而不需要进行核间的数据交换, 故这两层的计算量的差距仅限在初始计算时的数据传输量. 而在conv3_3, conv4_3和conv5_3中, 两种数据划分方法使得每个核分配的计算数据量的在高度和宽度方向上均有差别. 因为在这几层卷积层中, 如果按照一般的数据划分方法, 单个计算核只能计算得到高度为1的输出, 如conv3_3中, 一般的划分方法得到的输出是[0∶0, 0∶55], 接着进行卷积计算时, 需要偶数倍的输出, 即输出的数据应该为[0∶1, 0∶55]这种方式, 此时就需要进行核间的数据传输才能满足. 但是在优化的划分方法下, 即考虑了下一层所要进行的计算, 直接将数据划分为[0∶3, 0∶29], 将高度和宽度均进行了划分, 使得其输出结果[0∶1, 0∶27], 此时可以直接进行卷积计算, 而不需要进行数据传输, 降低了数据的传输, 同时又充分利用了计算资源, 单核的计算量也有所降低.
| 表 3 VGGNet-16网络结构 |
| 表 4 VGGNet-16网络的数据划分 |
本文实验通过统计计算各个层在完成计算时, 需要将数据进行传输以进行下一层次的计算, 以此计算各个层之间需要传输的数据量, 并与未优化的数据划分方式进行对比.
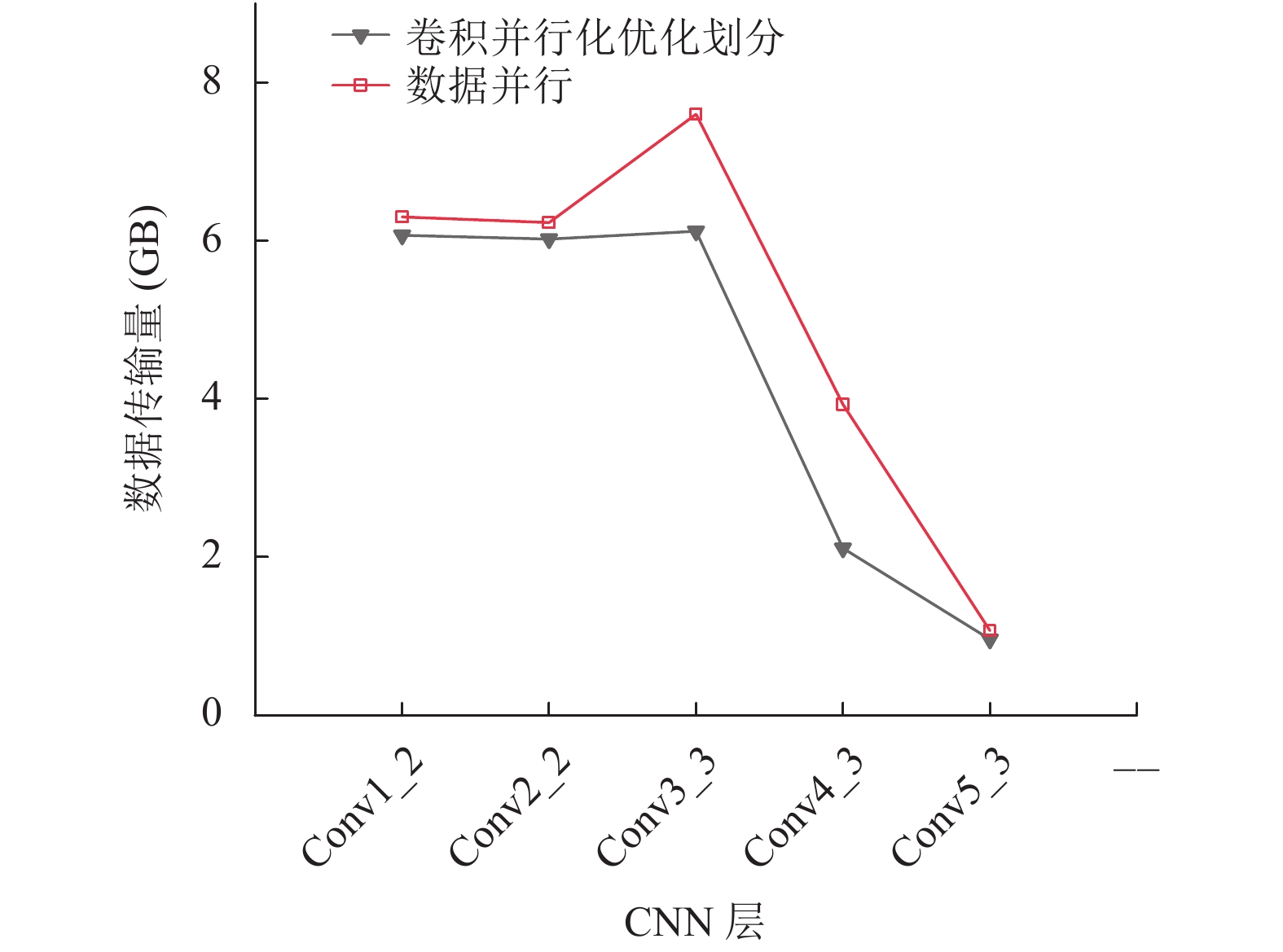
3.2 实验结果与分析本文基于数据并行与卷积操作特性结合的方式进行设计计算的任务划分, 并与只使用数据并行的方式的任务的划分进行对比实验, 通过实验统计两种方式下数据传输量来进行验证比较. 如图6所示为两种计算任务划分方法下数据传输量的比较图.
图6中在下方的黑色实心下三角所显示的折线是优化后的划分方式, 上方的空心方形显示的是仅考虑数据并行的划分方式. 实验结果表明, 优化的划分方式可以有效的减少数据量的传输. 图6显示优化前后的数据划分方法在各个卷积层的数据传输量均有所降低. 其中, 在conv1_2和conv2_2中由于优化前后的数据的划分分布均可以满足本地池化层的计算, 因此优化后的数据传输量只有小幅度的降低. 而在卷积层conv3_3、conv4_3和conv5_3时, 优化的数据划分方式充分考虑了计算核的负载均衡和池化层的特性, 在计算池化层时减少了数据量的传输, 使得优化后的数据传输量有明显的降低, 其中在conv4_3这一卷积层时, 优化后的数据传输量减少的效果比较明显, 其达到46.3%.
|
图 6 数据传输量对比图 |
4 总结与展望
为应对卷积神经网络模型复杂的规模和结构, 本文结合了卷积神经网络的结构特点和数据并行计算方法, 基于BWDSP众核架构对卷积计算任务进行了并行化划分的设计. 实验结果表明该方法相较于数据并行计算, 进一步降低了卷积计算时数据量的传输.
因为在全连接层的计算存在大量的权重参数, 与卷积层相比, 其计算是通信密集型的. 若采用卷积层的划分方式, 核间无法共享权重值, 数据的通信量较大. 因此, 需要对卷积神经网络的划分方法进一步完善和改进, 以降低全连接层计算的数据传输量.
| [1] |
LeCun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [2] |
Russakovsky O, Deng J, Su H, et al. ImageNet large scale visual recognition challenge. International Journal of Computer Vision, 2014, 115(3): 211-252. |
| [3] |
Gu JX, Wang ZH, Kuen J, et al. Recent advances in convolutional neural networks. Pattern Recognition, 2018, 77: 354-377. DOI:10.1016/j.patcog.2017.10.013 |
| [4] |
Le QV. Building high-level features using large scale unsupervised learning. Proceedings of 2013 IEEE International Conference on Acoustics, Speech and Signal Processing. Vancouver, BC, Canada. 2013. 8595-8598.
|
| [5] |
Chen TS, Du ZD, Sun NH, et al. DianNao: A small-footprint high-throughput accelerator for ubiquitous machine-learning. ACM Sigplan Notices, 2014, 49(4): 269-284. |
| [6] |
Parashar A, Rhu M, Mukkara A, et al. SCNN: An accelerator for compressed-sparse convolutional neural networks. ACM SIGARCH Computer Architecture News, 2017, 45(2): 27-40. DOI:10.1145/3140659 |
| [7] |
LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [8] |
CET38. BWDSPl00软件用户手册. 合肥: 中国电子科技集团第三十八研究所, 2011. 181–191.
|
| [9] |
邓文齐. 基于BWDSP的众核深度学习加速器的研究[硕士学位论文]. 合肥: 中国科学技术大学, 2018.
|
| [10] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA. 2016. 770–778.
|
| [11] |
Abadi M, Barham P, Chen JM, et al. Tensorflow: A system for large-scale machine learning. Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation. Savannah, GA, USA. 2016. 265–283.
|
| [12] |
Jia YQ, Shelhamer E, Donahue J, et al. Caffe: Convolutional architecture for fast feature embedding. Proceedings of the 22nd ACM International Conference on Multimedia. Orlando, Florida, USA. 2014. 675–678.
|
| [13] |
Hillis WD, Steele Jr GL. Data parallel algorithms. Communications of the ACM, 1986, 29(12): 1170-1183. DOI:10.1145/7902.7903 |
| [14] |
Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv: 1409. 1556, 2014.
|
 2019, Vol. 28
2019, Vol. 28



