1 引言

随着媒体技术的发展, 摄像设备已经成为我们生活中的一部分, 尤其在安防监控领域. 传统的摄像头采用CCD或者CMOS传感器, 这两类传感器均为在可见光范围内基于人眼的成像特性设计出的成像设备, 能建立与人眼成像特性一致的标准光谱响应函数, 从而使设备所显示色彩与人眼所感知的色彩一致^[1]. 在监控系统使用这类摄像头时, 需要在摄像头传感器前加入可以机械切换的红外滤波片装置, 该装置能够感应光照强度, 白天利用红外滤波片滤除红外光, 从而达到可见光成像; 当光照强度低于某个设置阈值, 系统会移除红外截止滤镜, 利用夜间红外光或红外补光灯成像. 在来回切换过程中会造成滤波片切换系统的磨损, 导致切换装置故障, 不能正确切换到位, 影响正常成像. 随着近几年算法研究的发展, 本文尝试使用算法的方式代替机械切换红外截止滤镜, 来滤除白天的红外光.

根据RGB图像的定义方式, 我们称混入IR近红外光的图像为四带图像(RGB三带和IR近红外带). 目前已有的文献中研究图像偏色的校正算法大多都是针对在可见光范围内的成像^[2], 对于混入IR的四带图像的校正研究中, 李林金^[3]根据四带图像的树木和背景区域之间受850 nm近红外光的影响不同, 提出分区域颜色校正方法. 晏嫚^[4]基于颜色空间特性, 对四带图像的特殊色域分布特性进行系统分析, 对图像的部分区域进行参考白平衡算法原理进行颜色校正算法处理. 但是由于现实中获取的图像多样化, 分区域处理就有很大的局限性. 曾兆斌^[5]提出利用构建三带图像与四带图像之间的线性回归关系, 求解校正矩阵的方法, 在室内四带图像颜色校正方面取得了突破. 但对室外四带图像校正效果不好.

对于四带图像, 本文从相机自身CMOS或CCD传感器的光谱响应特性受近红外光影响, 从而影响图像颜色的分析入手, 根据四带图像偏色的来源, 运用岭回归^[6,7]对相机自身的光谱响应特性进行校正.

2 基于岭回归的相机自身光谱特性校正

相机拍摄彩色图像的过程是拟合人眼对彩色感知的过程. 为了使彩色成像设备成像颜色与人眼感知颜色保持一致, CIE(国际照明委员会)建立了标准光谱响应函数(CIE1931-XYZ系统)用来拟合人眼对物体色彩的标准响应特性^[2]. 如图1所示, 曲线分别表示人眼对三种标准光源刺激值的响应函数曲线. 显然这个曲线只适用于可见光范围内, 对于我们项目中的四带图像而言, 由于在拍摄过程中直接去除了红外截止滤镜, 所以近红外的加入必然会影响相机的标准光谱响应曲线, 使其与人眼对三基色的响应曲线不一致. 所以本文尝试在四带图像校正中, 采用岭回归的彩色定标^[8]方法对相机自身的光谱响应特性进行校正.

2.1 岭回归的提出

岭回归(Ridge Regression)是由Hoerl和Kennard于1970年提出的. 是一种专用于共线性数据分析的有偏估计回归方法^[6–8], 实质上是一种改良的最小二乘估计法, 通过放弃最小二乘法的无偏性, 以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法, 相比于常用的线性回归方法^[9,10], 这种方法使模型均方差最小, 从而保证了模型泛化能力更强. 使用岭回归的方法校正相机光谱特性能使相机拍摄适应于更多的场景.

2.2 岭回归原理

对于相机光谱特性校正, 我们可以看成是基于机器学习的方法——岭回归问题. 其目的是寻找相机标准光谱特性曲线下拍摄的三带图像与加入红外光干扰的相机光谱特性曲线下拍摄的四带图像之间的回归函数关系^[10]. 典型的解决方法是最小二乘法(least square method), 其基本思想是假设标准光谱曲线对应的响应值为Y, 我们的目标就是寻找一个函数 $f(X) = {\beta ^{\rm{T}}}X$ , 存在 $\hat \beta $ , 使目标函数与原响应值之间的误差 $\varepsilon $ 的平方和达到最小, 即:

$ \begin{split} &\hat \beta = \arg \mathop {\min }\limits_\beta \left({\left(Y - f(X)\right)^2}\right) = \arg \mathop {\min }\limits_\beta \left( {\sum\limits_{i = 1}^m {\varepsilon _i^2} } \right) \\ &= \arg \mathop {\min }\limits_\beta \left( {\sum\limits_{i = 1}^m {{{\left({y_i} - {\beta ^{\rm{T}}}{x_i}\right)}^2}} } \right) \\ \end{split} $

(1)

为了使建立的回归模型的均方差最小, 使模型泛化能力更强. 岭回归提出在误差平方和基础上引入 $\lambda $ 来限制 ${\left\| \beta \right\|^2}$ 的大小, 通过加入惩罚项 $\lambda {\left\| \beta \right\|^2}$ , 能够保证 $\beta $ 在一定的范围内波动, 即:

$\hat \beta {\rm{ = }}\arg \mathop {\min }\limits_\beta \left( {\sum\limits_{i = 1}^m {{{\left({y_i} - {\beta ^{\rm{T}}}{x_i}\right)}^2} + \lambda {{\left\| \beta \right\|}^2}} } \right)$

(2)

根据文献[9], 可以求得岭回归系数值:

$\beta = {\left( {{X^{\rm{T}}}X + \lambda I} \right)^{ - 1}}{X^{\rm{T}}}Y$

(3)

其中, I是单位矩阵^[8], $\lambda $ 是控制对于 ${\left\| \beta \right\|^2}$ 增加的惩罚力度大小的调整参数^[7,8]. $\lambda $ 增大, 可以减小模型误差 $\varepsilon $ 的方差 $Var(\varepsilon )$ , 使泛化能力更强, 但是会增加模型误差 $\varepsilon $ 的偏差 $E(\varepsilon )$ ; $\lambda $ 减小, 则会减小模型误差 $\varepsilon $ 的方差 $Var\;(\varepsilon )$ , 增加模型误差 $\varepsilon $ 的偏差 $E\;(\varepsilon )$ ; 因此在岭回归中, 合适的 $\lambda $ 能够控制偏差与方差之间的平衡, 从而使模型泛化能力更强.

2.3 彩色定标

彩色定标^[11]采用颜色丰富的潘通色卡. 实验过程如下:

(1) 首先在实验室黑暗环境中, 使用D65标准光源箱, 并用850 nm的近红外光源直射已经移除红外截止滤镜的摄像头, 在棚中中拍摄潘通色卡的四带图像(RGB三带与IR近红外带), 如图2所示.

(2) 随后关闭近红外光源, 同机位拍摄潘通色卡的三带图像(RGB三带), 如图3所示.

(3) 根据获得的图2、图3的潘通色卡图像获取潘通色卡的三带和四带潘通色卡块, 用于获取校正矩阵. 此处用于实验的色块选取了30 块. 分别如图4、图5所示.

仔细观察图4和图5可以看到图5的最后一列的第三块色块相比于图4的同一块色块颜色明显偏红了, 其他对应序号色块也有不同程度的偏色. 也即是说明近红外光对摄像头响应曲线造成了影响.

假设一组数据样本, 四带图像一个色块的像素值( ${R_i}, {G_i}, {B_i}$ )是我们的观察数据, 三带图像对应色块的像素值 $\left( {{R_{si}},{G_{si}},{B_{si}}} \right)$ 是我们的目标数据, 用回归的方式将观察数据和目标数据进行拟合^[12,13]. 如式(4)所示:

$\left\{\begin{array}{l} {R_{si}} = {a_{11}}{R_i} + {a_{12}}{G_i} + {a_{13}}{B_i} + {a_{14}} \\ {G_{si}} = {a_{21}}{R_i} + {a_{22}}{G_i} + {a_{23}}{B_i} + {a_{24}} \\ {B_{si}} = {a_{31}}{R_i} + {a_{32}}{G_i} + {a_{33}}{B_i} + {a_{34}} \\ \end{array} \right.$

(4)

用矩阵形式^[14]表示, 如式(5)所示:

$Y = X{M^{\rm{T}}}$

(5)

其中,

$\begin{split}& X = \left[ {\begin{array}{*{20}{c}} {{R_1}}&{{G_1}}&{{B_1}}&1 \\ {{R_2}}&{{G_2}}&{{B_2}}&1 \\ \vdots & \vdots & \vdots & \vdots \\ {{R_{30}}}&{{G_{30}}}&{{B_{30}}}&1 \end{array}} \right],\;\;\;Y = \left[ {\begin{array}{*{20}{c}} {{R_{s1}}}&{{G_{s1}}}&{{B_{s1}}} \\ {{R_{s2}}}&{{G_{s2}}}&{{B_{s2}}} \\ \vdots & \vdots & \vdots \\ {{R_{s30}}}&{{G_{s30}}}&{{B_{s30}}} \end{array}} \right],\\ &M = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}&{{a_{14}}} \\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}&{{a_{24}}} \\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}}&{{a_{34}}} \end{array}} \right]\end{split} $

根据岭回归算法求解在RGB色彩空间下的颜色校正系数M.

$M = {({X^{\rm{T}}}X + \lambda I)^{ - 1}}{X^{\rm{T}}}Y$

(6)

这里在求解M的过程中, 涉及到调整参数 $\lambda $ 的确定, 在实验中我们通过获得的岭迹图, 使用广义交叉验证法(Generalized Cross-Validation, GCV)^[15]获得使模型均方差最小的调整参数 $\lambda $ . 以G分量为例, 即:

${Y_g} = {\left[ {\begin{array}{*{20}{c}} {{G_{s1}}}&{{G_{s2}}}& \cdots &{{G_{s30}}} \end{array}} \right]^{\rm{T}}}$

(7)

$X = \left[ {\begin{array}{*{20}{c}} {{R_1}}&{{G_1}}&{{B_1}}&1 \\ {{R_2}}&{{G_2}}&{{B_2}}&1 \\ \vdots & \vdots & \vdots &1 \\ {{R_{30}}}&{{G_{30}}}&{{B_{30}}}&1 \end{array}} \right]$

(8)

回归系数矩阵为 ${M_g} = \left[ {\begin{array}{*{20}{c}} {{a_{21}}}&{{a_{22}}}&{{a_{23}}}&{{a_{24}}} \end{array}} \right]$ .

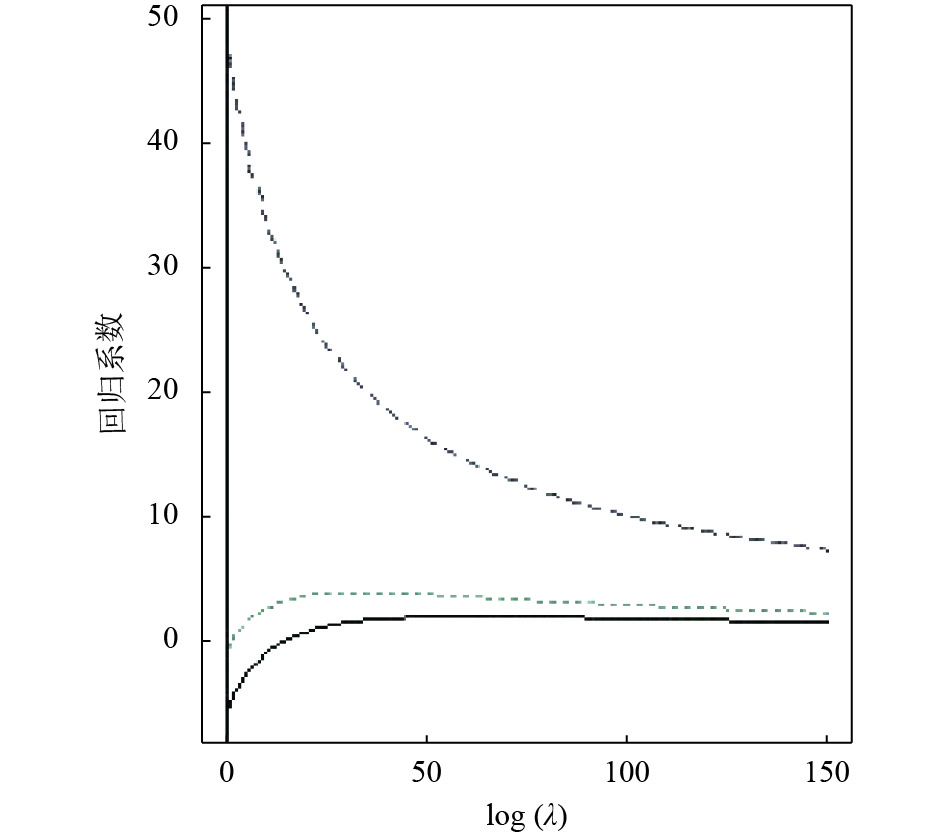
岭回归算法获得的岭迹图如图6所示, 该图绘制出了回归系数和 $\log (\lambda )$ 的关系, 通过交叉验证法, 可以在 $\lambda $ 分布范围中间某处找到使得预测结果最好的 $\lambda $ 值.

通过交叉验证得到在调整参数 $\lambda $ =0.002 603 838时的回归系数, 如表1所示.

同样的方法获得R、B两个分量的校正系数. 从而组成矩阵M.

$M = \left[ {\begin{array}{*{20}{c}} {1.00326}&{0.06593}&{ - 0.03833}&{ - 9.29167} \\ { - 0.04058}&{1.08286}&{ - 0.01184}&{5.27021} \\ { - 0.02370}&{ - 0.02254}&{1.04929}&{ - 2.77302} \end{array}} \right]$

然后我们就可以利用矩阵M对经过850 nm近红外光影响的相机响应函数进行校正. 由于我们难以直接获得相机的响应曲线, 这里我们对相机拍摄的四带图片进行岭回归校正, 根据校正效果反映相机响应函数的拟合程度, 校正结果如图7所示.

从对潘通色卡图校正结果可以看到经过岭回归校正后的四带图像整体上已经滤除了近红外光的影响, 与三带图像颜色的视觉效果更接近了. 也即是说我们通过岭回归获得的校正矩阵完成了与相机启用红外滤波片相似的视觉效果. 那么这个过程也即是完成了对受红外光影响的相机光谱响应曲线的校正.

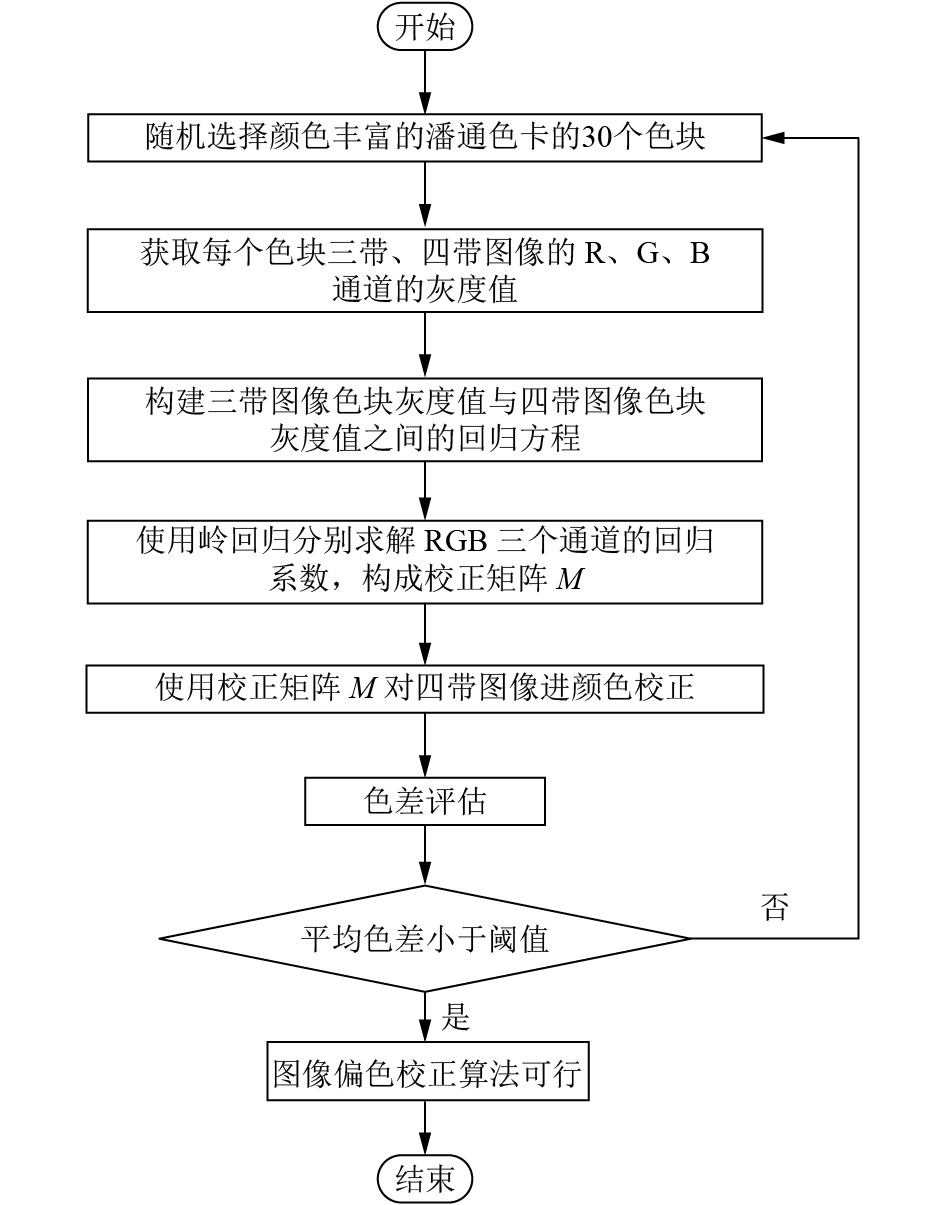
整个基于岭回归的四带图像偏色校正算法的流程如图8所示.

3 实验结果与分析

通过文中提出的岭回归分别对室内和室外四带图像进行校正. 在室内D65+850 nm近红外光情况下, 获取的四带图像经过传统白平衡算法和本文的岭回归算法校正前后结果如图9–图12所示.

对于室外图像, 使用室内岭回归获得的校正矩阵对室外四带图像的校正如图13–图15所示.

从校正前后对比图像可以看出本文的算法对于850 nm近红外光造成的实验室环境物体偏色以及室外色卡偏色有较好的校正结果. 针对室内与室外四带图像的校正结果, 为了便于对比每个色块的校正效果, 本文对分别对室内和室外24色卡三带与四带图像校正前后色差 $\Delta E$ 进行统计分析, 色差公式见式(9).

$\Delta E{\rm{ = }}\sqrt {{{({{{R}}_{\rm{1}}}{\rm{ - }}{{{R}}_{\rm{2}}}{\rm{)}}}^{\rm{2}}}{\rm{ + (}}{{{G}}_{\rm{1}}}{\rm{ - }}{{{G}}_{\rm{2}}}{{\rm{)}}^{\rm{2}}}{\rm{ + (}}{{{B}}_{\rm{1}}}{\rm{ - }}{{{B}}_{\rm{2}}}{{\rm{)}}^{\rm{2}}}} $

(9)

实验结果对比图如图16、图17所示, 其中纵坐标表示R、G、B三个分量在校正前后与标准三带图像色差值, 横坐标表示24色块编号.

从两幅色差曲线图可以看出经过岭回归校正后, 大多数点的色差曲线更接近于0, 也即是表明经过岭回归校正后的图像颜色更接近于三带图像的颜色; 室内24色卡校正后的色差曲线相比于室外24色卡校正后的色差曲线更趋近于0. 说明室内获取的岭回归校正矩阵对同种光源环境获取的四带图像更好的校正效果; 室外24色卡校正后的色差曲线相比于校正前也更趋近于0, 说明室内获取的校正矩阵对室外其他光源环境拍摄的四带图像也有一定的校正效果.

4 结论与展望

针对有近红外光串扰的四带图像的颜色校正问题, 本文在不改变摄像机传感器的情况下, 从850 nm近红外光对传感器响应函数的影响角度考虑, 通过岭回归的彩色定标方法对相机自身的光谱特性进行校正. 实验表明, 该方法获取的校正矩阵, 可以对不同光照环境下的不同四带图像有良好的校正结果. 这对于三带图像受红外光污染的图像颜色校正有一定的参考价值.