引言

支持向量机(Support Vector Machines, SVM)是一种应用广泛的机器学习方法, 具有理论知识清晰完备, 适应性和泛化能力良好的优点, 核心思想是在特征空间中寻找到一个最优超平面将两类样本尽可能大的分开, 能够较好的处理小样本、非线性和克服“维数灾难”问题, 并且表现出优秀的分类能力和泛化能力而被广泛应用于分类和回归等领域. 但是SVM对核函数的参数选取对分类效果影响很大, 不合适的参数可能使得分类器性能大大降低.

针对SVM核参数的选取问题, 目前尚没有统一有效的方法. 传统的参数选择方法如实验法、网格搜索法等由于耗时过长和不必要的验证流程等缺点, 更常用的方法是群智能算法如蚁群算法、遗传算法和粒子群算法等优化支持向量机核参数.

粒子群算法由于算法结构简单、寻优能力相对较好, 近年来选择粒子群算法优化SVM参数成为研究热点之一. 如文献[1]用标准粒子群算法对SVM参数进行优化, 并将该模型应用于聚丙烯腈生产的软测量模型中, 通过与标准SVM比较, 证明了所提方案有效性; 随着研究深入, 标准PSO算法在应用过程中暴露出不少的缺点, 如易陷入局部最优值、后期收敛的速度较慢等缺点, 因此研究者也对其提出不少改进方法, 如文献[2–4]等通过改进惯性权值, 或者改变学习机制等方法以提高粒子群算法性能.

本文通过引入非线性惯性权值递减和异步线性变化的学习因子策略改进粒子群算法, 并且通过机器学习公开数据集UCI数据集的实验数据证明了其有效性.

1 支持向量机基本思想和参数

支持向量机是由Vapnik等人在1995年提出的基于统计学理论和结构风险最小化原理的机器学习方法, 其基本思想是找到一个分类面将两类样本分开. 当线性可分时, 其最优的分类面要求正确地将样本分开且分类间隔最大; 当线性不可分时, 寻找一个多维超平面从而将样本分开.

对于训练样本集: $\left({x_1},{y_1}\right),(x{}_2,{y_2}),\cdots,({x_N},{y_N}),x \in {R^n},$ $y \in \left( { - 1,1} \right) $ 最优分类超平面的二次规划问题如下:

$\left\{ \begin{split} &{min\frac{1}{2}{w^{\rm{T}}} \times w + C\sum\limits_{i = 1}^N {{x_i}} }\\ &{{\rm s.t.}\;\;{y_i}\left({w^{\rm{T}}}{x_i} + b\right) \ge 1 - {\xi _i},\;{\xi _i} \ge 0,\;i = 1,2,\cdots,N} \end{split}\right.$

(1)

其Lagrange函数为:

$\begin{split} L(w,b,l) =& \frac{1}{2}{w^{\rm{T}}} \times w + C\sum\limits_{i = 1}^N {{z_i}} \\ &- \sum\limits_{i = 1}^N {{l_i}\left[{y_i}\left({w^{\rm{T}}}{x_i} + b\right) - 1 + {x_i}\right] - \sum\limits_{i = 1}^N {{a_i}{x_i}} } \end{split}$

(2)

式中, ${\lambda _{\rm{i}}} \geqslant 0,i = 1,2, \cdot \cdot \cdot ,N$ . 式(1)的对偶问题可表示为:

$\left\{ \begin{split} &{\max Q(l) = \sum\limits_{i = 1}^N {{l_i}} - \frac{1}{2}\sum\limits_{i,j = 1}^N {{y_i}{y_j}{\lambda _i}{\lambda _j}\left({x_i}.{x_j}\right)} }\\ &{{\rm s.t.}\sum\limits_{i = 1}^N {{y_i}{\lambda _i} = 0,\;0 \le {\lambda _i} \le C} } \end{split}\right.$

(3)

可得决策函数为:

$f(x,l) = sgn\left(\sum\limits_{SV} {{y_i}{\lambda _i}\left({x_i}.{x_j}\right) + b} \right)$

(4)

对线性不可分的对偶函数为:

$\left\{ \begin{split} &\max Q(\lambda ) = \sum\limits_{i = 1}^N {{\lambda _i}} - \frac{1}{2}\sum\limits_{i,j = 1}^N {{\lambda _i}{y_j}{\lambda _i}{\lambda _j}\left({\phi _{{x_i}}} \times {\phi _{{x_j}}}\right)} \\ &{\rm s.t.}\sum\limits_{i = 1}^N {{y_i}} {\lambda _i} = 0,\;0 \le {\lambda _i} \le C \end{split}\right.$

(5)

式中, ${\varphi _{{x_i}}} \times {\varphi _{{x_j}}} = K({x_i},{x_j})$ 即为核函数, 其决策函数为:

$f(x,l) = sgn\left(\sum\limits_{SV} {{y_i}{\lambda _i}} K\left({x_i},{x_j}\right) + b\right)$

(6)

不同的核函数可以生成不同的支持向量机分类器, SVM中常用的核函数有线性核、多项式核、径向基核和Sigmoid核函数等. 本文选择径向基核函数作为SVM的核函数, 即:

$K({x_i},x) = \exp (\gamma {\left\| {{x_i} - x} \right\|^{_2}})$

(7)

其中, $\gamma = \dfrac{1}{{2{\sigma ^2}}}$ .

影响核函数的参数有惩罚银子C和核函数 $\sigma $ , 惩罚因子C是对错分的样本的惩罚程度的控制, 越大表示惩罚越重, 但其泛化能力也会同时降低. $\sigma $ 是核函数的宽度参数, 表示对径向范围的控制. 惩罚因子C和核函数 $\sigma $ 的选取对SVM分类器影响至关重要, 因此要获得优秀的支持向量机的分类性能, 需要选取合适的C和 $\sigma $ ^[5].

2 改进粒子群算法优化SVM 2.1 粒子群算法概述

粒子群算法是基于对鸟类的捕食过程进行模拟的一种新型智能仿生优化算法. 该算法把群体中的个体视为多维空间中的一个没有质量和体积的点, 且以一定的速度飞行, 在此迭代过程中根据自身的飞行经验和同伴的飞行经验对自身的飞行速度进行动态调整以修正前进方向和速度大小. 粒子群算法就是通过每个粒子由适应度函数调整粒子至较优的区域以搜寻到问题的最优解.

PSO初始化一群随机粒子(粒子不考虑质量和体积), 粒子在N维空间位置表示为矢量 ${x_i} = ({x_1},{x_2}, $ $\cdots,{x_n})$ , 飞行速度表示为矢量 ${v_i} = ({v_1},v{}_2,\cdots,{v_n})$ , 每个粒子都有一个由目标函数确定的适应值(fitness value), 其个体最好位置p_best值和整个群体中发现的最好的位置g_best值以及当前位置, 通过迭代找到最优解, 在每次迭代中粒子通过p_best值和g_best值来更新自己.

$\left\{ \begin{aligned} & {v_i} = w{v_i} + {c_1}{r_1}(p_{{\rm{best}}{i}} - {x_i}) + {c_2}{r_2}(g_{{\rm{best}}{i}} - {x_i}) \\ & {x_i} = {x_i} + {v_i} \end{aligned} \right.$

(8)

式中, p_best表示粒子i是个体最优值, g_best表示粒子群的全局最优值; C₁和C₂是两个常数, 称为学习因子; r₁, r₂是0到1的随机数; w被称为惯性因子, w的值越大, 全局寻优能力越强, 收敛越慢, w值越小, 局部寻优能力越强, 收敛较快.

2.2 粒子群优化算法和支持向量机参数选择

惯性权重是粒子群算法中一个重要的参数之一, 它控制了全局搜索能力和局部搜索能力的平衡. 传统的粒子群算法有一些缺点, 如容易陷入局部最优值和后期震荡和收敛速度慢等, 国内外学者对算法的改进展开了研究. 文献[6]提出惯性权重进行了研究, 提出惯性权重w从0.9至0.4的线性递减的策略能够保证有更好的全局搜索能力和后期的局部搜索能力; 文献^[7]在递减的惯性权值的基础上, 提出了抛物线和指数曲线的非线性的权值递减策略; 文献[8]提出一种惯性权重线性递增的粒子群算法; 文献[9]提出一种惯性权重先增后减的粒子群算法; 文献[10]提出一种非线性递减的惯性权重粒子群算法; 文献[11,12]提出了惯性权重指数递减和余弦递减的粒子群算法; 文献[13]提出了一种惯性权值随粒子的位置和目标函数性质变化的动态改变惯性权重的粒子群算法等.

1) 具有非线性递减惯性权重粒子群算法

本文使用非线性递减权值策略将惯性权值w设置为变量, 通过非线性递减权值实现粒子的调整, (当n=1时, 即Shi提出的线性递减惯性权重策略), 其公式如下:

$w(k) = {w_{\rm{end}}} + {\left(\frac{{{i_{\rm{max}}} - i}}{{{i_{\rm{max}}}}}\right)^n}.\left({w_{\rm{ini}}} - {w_{\rm{end}}}\right)$

(9)

式中, ${w_{\rm{ini}}}$ 、 ${w_{\rm{end}}}$ 分别为 $w$ 的最大值和最小值, $i$ 表示当前迭代次数, ${i_{\rm{max}}}$ 表示最大迭代次数, n是指数值.

2) 异步线性改变学习因子策略

由标准粒子群算法公式(8)可知, C₁控制了“自我认知”部分, 即粒子自身之前的飞行经验对之后飞行方向的影响, C₂控制了“社会认知”部分, 即种群中所有粒子的飞行经验对每个粒子之后飞行方向的影响. 在标准粒子群算法中, Shi等建议C₁和C₂都取值为2, 在其他文献中有学者也提出C₁和C₂可以取不同的值, 其取值也基本在0至4之间.

学习因子在过程中采用不同的变化策略称之为异步变化. A.Ratnawecra等提出了一种异步线性改变学习因子的策略^[14], 该策略是在算法早期阶段C₁取值较大而C₂取值较小, 使粒子能够更多地向自我的学习以此加强全局搜寻能力; 在搜寻的后期阶段C₂取值较大, 使粒子能够快速收敛到全局最优解. 学习因子的更新公式如下:

$\left\{ \begin{gathered} {c_1} = {c_1}_{ini} - ({c_{1ini}} - {c_{1fin}})(t/{T_{max}}) \\ {c_2} = {c_2}_{ini} + ({c_{2fin}} - {c_{2ini}})(t/{T_{max}}) \\ \end{gathered} \right.$

(10)

式中, ${c_{1ini}}$ 、 ${c_{2ini}}$ 分别表示学习因子的初始值; ${c_{1fin}}$ 、 ${c_{2fin}}$ 分别表示学习因子的迭代最终值; t和T_max分别表示当前迭代次数和最大迭代次数.

综上所述, 本文引入非线性递减惯性权重和异步线性改变学习因子的粒子群优化算法, 用以寻找SVM模型中的惩罚因子 $C$ 和核函数参数 $\sigma $ 最优解, 每个粒子的位置代表为( $C$ , $\sigma $ ).

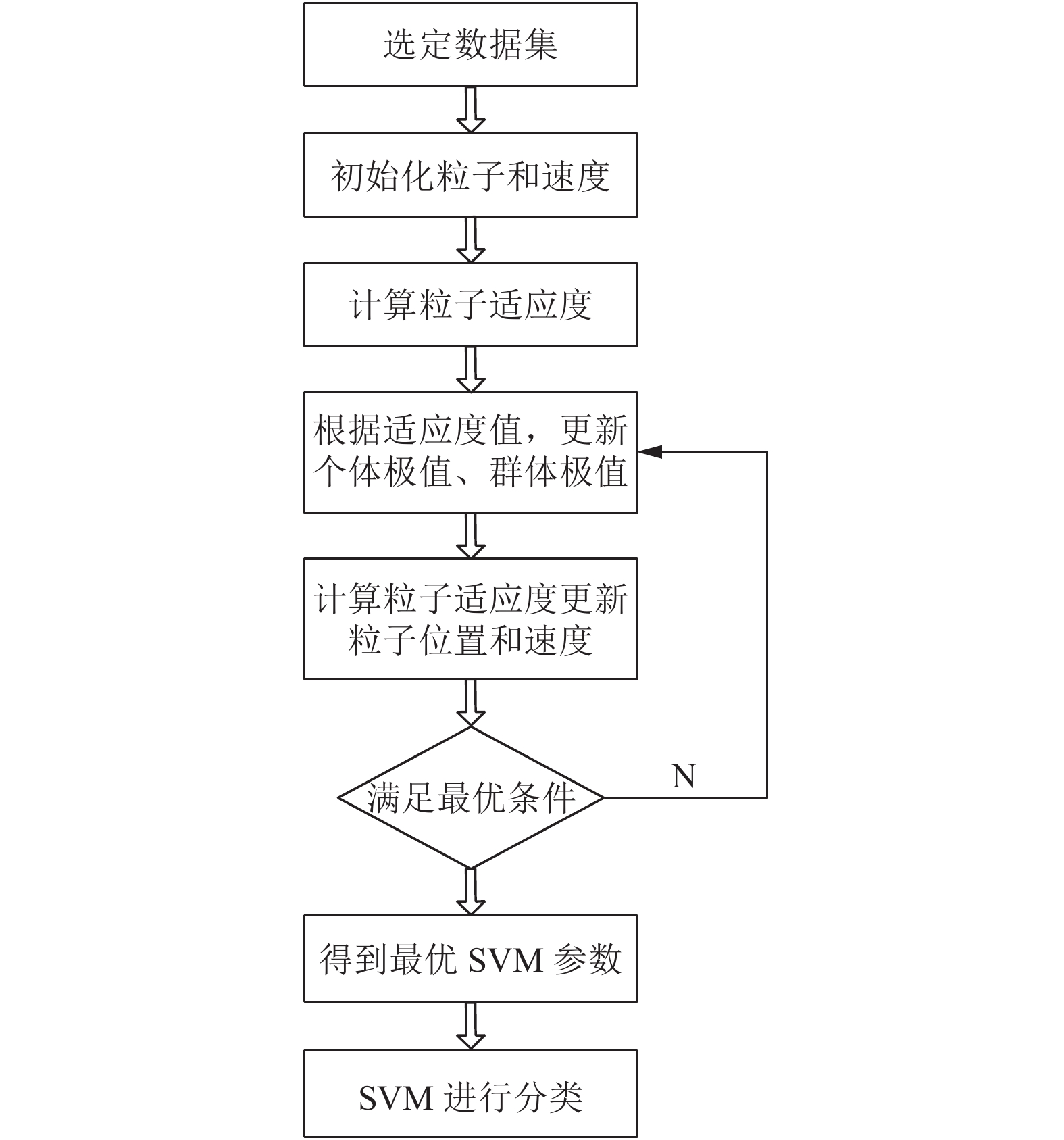
其算法流程如下,

① 初始化参数设置, 包括设置粒子种群规模、粒子维数、最大迭代次数、惯性权重最大值和最小值和指数值、加速因子初始值和迭代最终值、随机产生粒子初始位置和速度、个体极值和全局极值.

② 根据式(8)~式(10) 更新每个粒子的速度和位置.

③ 根据适应度函数计算粒子的适应度值.

④ 将粒子的当前适应度值和粒子个体极值进行比较, 若优于粒子个体极值, 则进行替换.

⑤ 若当前粒子的适应度值优于全局极值的适应度值, 则用当前粒子适应度值替换全局极值.

⑥ 若达到最大迭代次数, 则输出迭代出的最优解( $C$ , $\sigma $ ), 输出; 否则返回至步骤② .

⑦ 将优化后的 $C$ 和 $\sigma $ 利用SVM分类器进行训练, 并用文本测试集进行测试.

本算法优化过程图如图1所示.

3 实验与分析

实验所用硬软件环境信息如下, AMD A6-3420M APU with Radeon (tm), RAM 4 GB (含一2 GB samsung内存条), Windows 8 64位, 平台为Matlab R2014a.

为了验证本文提出的粒子群优化的支持向量机分类模型的有效性, 本文选取了机器学习公开数据集UCI的4组数据进行测试, 下载地址如下: http://archive.ics.uci.edu/ml/datasets.html.

3.1 实验参数设定

在参考大量文献之后^[1,5–7,15], 本文对粒子群参数作出如下合理设置. 种群规模 $N{\rm{ = }}20$ , 最大迭代次数 ${T_{\rm{max}}} = 100$ , 惩罚因子C最小值 ${C_{\rm{min}}} = {2^{ - 5}}$ , 最大值 $ {C_{\rm{max}}} = $ ${2^{15}}$ , 误差阈值为 ${10^{ - 3}}$ , 核参数 $\sigma $ 的最小值 ${\sigma _{{\rm{min}}}} = {2^{ - 15}}$ , 最大值 ${\sigma _{{\rm{max}}}} = {2^3}$ , 惯性因子最小值 ${w_{{\rm{end}}}} = 0.4$ , 惯性因子最大值 ${w_{\rm{ini}}} = 0.9$ , 非线性递减惯性权重粒子群算法中的指数 $n = 1.2$ , ${C_{1\rm{ini}}} = 2$ , ${C_{1\rm{fin}}} = 0.5$ , ${C_{2\rm{ini}}} = 0.5$ , ${C_{2\rm{fin}}} = 2$ ; 标准粒子群算法的 $w = 0.9$ , ${C_1} = {C_2} = 2$ ;

3.2 实验结果

在表1的数据集通过采用K折交叉验证法(K-fold cross validation), 即把表1中的每个样本数据随机地分为K个子样本集, 每次都去一个子样本集作为测试集, 剩余K–1个样本集作为训练集, 以此进行验证.

如下表2所示, 通过标准粒子群优化支持向量机算法^[1]和本文提出粒子群优化算法在UCI数据集上的实验结果, 表中的最大值、最小值和平均值表示经过了10-fold CV交叉验证后的分类准确率的最大值、最小值和平均值. 图2为两种算法在数据集上的准确率平均值对比图.

4 结论

支持向量机模型的分类精确率很大程度上由关键参数的选取决定, 本文引入非线性递减惯性权重和异步线性变化的学习因子策略. 随着迭代次数增加, 学习因子C₁的值减小而C₂值增加, 保证了前期个体最优质影响和后期全局最优解的影响, 加快后期的收敛; 而非线性递减惯性权重在保证粒子在迭代初期对整个搜索空间能进行快速搜索, 随着惯性权重非线性减小能使大部分搜索范围集中于最优值邻域中, 使搜索速度和精度都有提高. 实验结果表明, 非线性递减惯性权重和异步线性改变学习因子粒子群算法优化支持向量机比标准粒子群优化的支持向量机有更高的分类精确度和效率.