互联网的快速发展和电子商务规模的不断扩大, 导致信息过载情况日益严重^[1]. 用户无法在大量的信息中快速找到自己喜欢的信息, 因此推荐系统应运而生. 推荐系统根据用户之前的行为信息发现其信息需求, 从而将用户喜欢的信息进行推送^[2]. 其中, 协同过滤推荐算法是目前应用于各电商最广泛的个性化推荐算法. 由于基于用户的协同过滤算法更能推送新颖的项目, 因此得到更为广泛的应用^[3]. 然而, 基于用户的协同过滤算法仅考虑到用户间评分信息, 很难保证推荐质量, 因此, 新用户的冷启动、数据稀疏性和推荐准确性依旧目前亟待解决的难题.

随着对推荐算法研究的深入, 许多学者提出了新的相似性改进算法来改善传统协同过滤算法的不足. Liu^[4]等基于随机游走技术, 提出来一种用户之间非对称的相似性, 来提高推荐性能, 但这只是一个局部相似性指标, 在信息过滤技术上仍有缺陷. Li^[5]等提出了一种基于信任度的相似性算法, 利用用户的直接信任来改善推荐算法中数据稀疏性问题. Ma^[6]等提出了将用户评级和社会信任评级相结合的算法, 并验证此混合算法能有效提高推荐性能, 但不能改善矩阵稀疏性和冷启动问题. 陈颖^[7]等提出了基于项目属性偏好挖掘的相似性算法, 来缓解矩阵稀疏性. 董立岩^[8]等提出一种将时间融入到评分矩阵中的算法, 以提高推荐准确性.

上述这些研究只专注某一点来提高推荐效果, 以用户项目评分矩阵为主要数据来源, 却忽略了用户本身的属性特点, 有很多局限性. 针对以上分析, 本文提出一种基于用户特征的协同过滤推荐算法. 该算法结合属性特征、兴趣度、信任度和评分矩阵等信息来计算用户间综合相似性, 进而产生推荐. 在利用评分矩阵的基础上, 改进的相似性方法的主要贡献点如下:

(1) 结合属性特征. 属性特征是用户自身的特征信息, 表明了用户的生活状态. 通过分析属性特征的相似性可以改善用户冷启动问题, 并提高推荐准确性.

(2) 结合兴趣度. 兴趣度是推荐系统的推荐依据, 若分析出用户的兴趣, 则可大大的提高推荐准确性.

(3) 结合信任度. 信任度可以分为直接信任度和间接信任度, 直接信任度可以提高推荐准确性, 间接信任度可以填充评分矩阵, 提高准确性的同时还能改善数据稀疏性.

1 传统的基于用户的协同过滤推荐算法

基于用户的协同过滤算法的理论是, 如果不同用户对于某些项目具有相同的兴趣, 那么他们对于其他的项目也有着相似的兴趣^[9]. 该算法首先找出相似用户喜欢的项目, 然后预测目标用户对目标项目的评分, 最后将评分靠前的项目给用户做推荐.

1.1 用户-项目评分矩阵

对于 $m$ 个用户 $n$ 个项目的推荐问题, 可以构建 $m \times n$ 的用户-项目评分矩阵 $R(m, n)$ , 如表1所示. 矩阵中第 $i$ 行第 $j$ 列的 ${R_{i, j}}$ 表示用户 $i$ 对项目 $j$ 的评分.

1.2 相似性计算方法

(1) 余弦相似性. 用户的评分数据可以设为 $n$ 维向量, 那么两用户之间的相似度可看成两用户的评分向量夹角的余弦值. 若用户对某个项目没有评分, 则默认值为0.设两个用户 $x$ 和用户 $y$ 之间的评分向量分别为 $u$ 和 $v$ , 则 $x$ 和 $y$ 之间的余弦相似性 $sim(x, y)$ 如式(1)所示.

$sim(x, y) = \cos (u, v) = \frac{{\vec u \times \vec v}}{{\left\| {{\kern 1pt} \vec u{\kern 1pt} } \right\|\, \left\| {{\kern 1pt} \vec v{\kern 1pt} } \right\|}}$

(1)

(2) 修正的余弦相似性. 综合考虑不同用户间评分的标准不一样的情况. 设 ${R_{uv}}$ 表示用户 $u$ 和用户 $v$ 的共同评分集合, ${R_u}$ 表示用户 $u$ 的评分集合, $\overline {{R_u}} $ 表示用户 $u$ 所有评分的均值, ${R_v}$ 表示用户 $v$ 的评分集合, $\overline {{R_v}} $ 表示用户 $v$ 所有评分项的均值, 则用户 $u$ 和用户 $v$ 的修正余弦相似性 $sim(u, v)$ 如式(2)所示.

$sim(u, v) = \frac{{\displaystyle \sum\limits_{i \in {R_{uv}}} {({R_{u, i}} - \overline {{R_u}} ) \times ({R_{v, i}} - \overline {{R_v}} )} }}{{\sqrt {\displaystyle \sum\limits_{i \in {R_u}} {{{({R_{u, i}} - \overline {{R_u}} )}^2}} } \times \sqrt {\displaystyle \sum\limits_{i \in {R_v}} {{{({R_{v, i}} - \overline {{R_v}} )}^2}} } }}$

(2)

(3) 皮尔逊相关相似性. 设 ${R_{uv}}$ 表示用户 $u$ 和用户 $v$ 的共同评分集合, ${R_{u, i}}$ 表示用户 $u$ 对项目 $i$ 的评分, ${R_{v, i}}$ 表示用户 $v$ 对项目 $i$ 的评分, $\overline {{R_u}} $ 表示用户u所有评分的均值, $\overline {{R_v}} $ 表示用户所有v评分项的均值, 则用户u和用户v的皮尔逊相关相似性 $sim(u, v)$ 如式(3)所示.

$sim(u, v) = \frac{{\displaystyle \sum\limits_{i \in {R_{uv}}} {({R_{u, i}} - \overline {{R_u}} ) \times ({R_{v, i}} - \overline {{R_v}} )} }}{{\sqrt {\displaystyle \sum\limits_{i \in {R_{uv}}} {{{({R_{u, i}} - \overline {{R_u}} )}^2}} } \times \sqrt {\displaystyle \sum\limits_{i \in {R_{uv}}} {{{({R_{v, i}} - \overline {{R_v}} )}^2}} } }}$

(3)

1.3 评分预测

一般在进行评分预测时选取K近邻的方法^[10], 即将相似度最高的前K个用户作为最近邻来进行评分预测. 设集合 ${N_u}$ 为目标用户的邻居集合, ${R_{v, i}}$ 表示用户 $v$ 对项目 $i$ 的评分, 则用户 $u$ 对未评分项 $i$ 的预测评分值 ${P_{u, i}}$ 如式(4)所示.

${P_{u, i}} = \overline {{R_u}} + \frac{{\displaystyle \sum\limits_{v \in {N_u}} {sim(u, v) \times ({R_{v, i}} - \overline {{R_v}} )} }}{{\displaystyle \sum\limits_{v \in {N_u}} {sim(u, v)} }}$

(4)

2 基于用户特征的协同过滤推荐算法

传统的基于用户的相似度计算方法一般只计算评分间相似性, 却忽略了用户其他方面的相似性^[10]. 本文的用户特征综合考虑用户属性、用户兴趣度、用户信任度和用户评分等因素, 可以得到更加准确全面的相似度.

2.1 用户属性特征相似性建模

(1) 性别相似度. 如果用户之间的性别不同, 那么对项目的偏好也会有很大的差异, 比如女性用户选择项目时喜欢货比三家, 更加侧重美观性, 而男性用户却大多关注项目的可用性, 因此本文提取性别来作为属性的一部分. 设用户 $u$ 的性别为 ${S_u}$ , 用户 $v$ 的性别为 ${S_v}$ , 则用户 $u$ 和用户 $v$ 的性别相似度 $S(u, v)$ 如式(5)所示.

$S(u, v) = \left\{ {\begin{array}{*{20}{c}} {0\quad \quad {S_u}{\kern 1pt} \ne {\kern 1pt} {S_v}} \\ {1\quad \quad {S_u}{\kern 1pt} = {\kern 1pt} {S_v}} \end{array}} \right. $

(5)

(2) 年龄相似度. 年龄不同的用户所处环境不同, 看待问题的角度也不尽相同, 因此对项目种类的喜欢也会各有千秋^[11]. 设用户 $u$ 的年龄为 ${A_u}$ , 用户 $v$ 的年龄为 ${A_v}$ , 则用户 $u$ 和用户 $v$ 的年龄相似性 $A(u, v)$ 如式(6)所示.

$A(u, v) = \left\{ {\begin{array}{*{20}{l}} {\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1\quad {\kern 1pt} \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \quad \left| {{A_u} - {A_v}} \right| \leqslant 5} \\ {\dfrac{5}{{\left| {{A_u} - {A_v}} \right|}}\quad \quad \left| {{A_u} - {A_v}} \right| > 5} \end{array}} \right. $

(6)

(3) 职业相似度. 将职业分类描述成一个树形结构, 如图1中两个任意节点的长度设为1, 用 $Height$ 来表示总长度, 职业 $a$ 和职业 $b$ 最近的父节点在职业树中的层数称为它的高度, 记 ${H_{a, b}}$ . 用户 $u$ 和用户 $v$ 的职业分别用职业 $a$ 和职业 $b$ 表示, 则职业相似性 $O(u, v)$ 如式(7)所示.

$ O(u, v) = si{m_o}(a, b) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{H_{a, b}}}}{{Height}}\quad \quad a \ne b} \\ {\quad \;\, 1\;\quad \quad \quad a = b} \end{array}} \right. $

(7)

(4)用户属性相似性. 将上述性别、年龄和职业三个属性综合起来, 则用户 $u$ 和用户 $v$ 的属性相似度 $si{m_a}(u, v)$ 如式(8)所示.

$ si{m_a}(u, v) = {\rm{\alpha}} S(u, v) + {\rm{\beta}} A(u, v) + {\rm{\gamma}} O(u, v) $

(8)

其中, ${\rm{\alpha }}$ 、 ${\rm{\beta}} $ 、 ${\rm{\gamma}} $ 为各个属性的权重系数, 分别影响性别、年龄和职业在用户属性相似度上所起的作用. 其中, ${\rm{\alpha }}$ 、 ${\rm{\beta}} $ 、 ${\rm{\gamma}} \in [0, 1]$ , 且 ${\rm{\alpha }} + {\rm{\beta}} + {\rm{\gamma}} = $ 1, 不同的推荐系统, 可以动态调整其值以达到不同的推荐效果.

融合用户属性相似度 $si{m_a}(u, v)$ 与传统的皮尔逊相似度 $sim(u, v)$ , 得到用户属性综合相似度 $si{m_p}(u, v)$ 如式(9)所示, 其中, ${\rm{\xi}} $ 为调整属性综合相似度的系数, ${\rm{\xi}} \in [0, 1]$ .

$ si{m_p}(u, v) ={\rm{\xi}} si{m_a}(u, v) + (1 - {\rm{\xi}} )sim(u, v) $

(9)

2.2 用户兴趣特征相似性建模

传统的基于用户的相似度计算方法一般只计算评分间相似性, 没有考虑到用户对某类项目的喜好. 若两个用户间评分项目属性比较相近, 则两个用户间也可认为具有较高的相似性, 因此考虑到用户兴趣特征的相似性构建方法如下面的模型.

把用户对某种项目属性的喜好当作用户的兴趣特征, 那么用户对某种项目的评价数目越多, 则对这种项目的兴趣度就越大^[12]. 设 $N{I_{u, i}}$ 表示用户 $u$ 对 $i$ 类项目的评价总数, $N{I_u}$ 表示用户已评价的项目总数, 那么用户 $u$ 对某种项目的兴趣度 ${I_{u, i}}$ 如式(10)所示.

${I_{u, i}} = \frac{{N{I_{u, i}}}}{{N{I_u}}}$

(10)

通过得到用户对每个种类项目的兴趣度, 则可计算出用户之间的兴趣相似度. 设用户 $u$ 的兴趣度用集合 ${I_u} = ({I_{u, 1}}, {I_{u, 2}}, \cdots , {I_{u, i}})$ 表示, ${I_{uv}}$ 表示用户 $u$ 和用户 $v$ 共同评分的项目种类数, $\overline {{I_u}} $ 表示用户 $u$ 对所有项目种类的平均用户兴趣度, 基于式(3), 任意两个用户间的兴趣相似度 $si{m_I}(u, v)$ 如式(11)所示.

$ si{m_I}(u, v) = \frac{{\displaystyle \sum\limits_{i \in {I_{uv}}} {({I_{u, i}} - \overline {{I_u}} ) \times ({I_{v, i}} - \overline {{I_v}} )} }}{{\sqrt {\displaystyle \sum\limits_{i \in {I_{uv}}} {{{({I_{u, i}} - \overline {{I_u}} )}^2}} } \times \sqrt {\displaystyle \sum\limits_{i \in {I_{uv}}} {{{({I_{v, i}} - \overline {{I_v}} )}^2}} } }} $

(11)

最后将用户兴趣相似度 $si{m_I}(u, v)$ 与用户属性综合相似度 $si{m_p}(u, v)$ 通过式(12)来计算属性兴趣相似度 $si{m_z}(u, v)$ , 其中, 动态调整 ${\rm{\delta }} $ 以达到不同的推荐效果, ${\rm{\delta }} \in [0, 1]$ .

$ si{m_z}(u, v) = {\rm{\delta }} si{m_I}(u, v) + (1 - {\rm{\delta }} )si{m_p}(u, v) $

(12)

2.3 用户信任度相似性建模

信任度是指在为用户做项目做推荐时, 其他用户的参考程度, 对一个用户越信任, 其参考程度越大. 考虑到用户间分为有共同评分和没有共同评分两种情况, 则将信任度分为直接信任度和间接信任度. 直接信任度表示有直接关联的用户相似性, 间接信任度表示没有直接关联却可能存在关联的用户相似性^[13].

在用户项目评分矩阵中, 若两用户间有共同评分则矩阵中评分值不为0, 若没有共同评分则矩阵中评分值为0.在引入间接信任度的概念后, 若两用户间没有共同评分, 且间接信任度值不为0, 则可以填充评分矩阵, 在一定程度上缓解了矩阵稀疏性问题.

(1) 直接信任度

在一个用户为另一个用户推荐的项目中, 可以把被推荐用户满意的项目的比例作为初始信任度.

根据式(4)的预测机制, 可得到用户 $u$ 为用户 $v$ 在第 $i$ 个项目上的预测评分值, 设 $\overline {{R_v}} $ 表示目标用户 $v$ 对已经评论项目的平均评分, $\overline {{R_u}} $ 表示目标用户 $u$ 对已经评论项目的平均评分, $R{}_{u, i}$ 表示用户 $u$ 对第 $i$ 个目标项目的评分, 其中 $sim(u, v)$ 使用式(3), 则预测评分公式 ${P_{u, v, i}}$ 如式(13)所示.

$ {P_{u, v, i}} = \overline {{R_v}} + ({R_{u, i}} - \overline {{R_u}} ) \times sim(u, v) $

(13)

如果用户 $u$ 预测用户 $v$ 对于第 $i$ 个项目的评分值 ${P_{u, v, i}}$ 与用户 $v$ 的真实评分 ${R_{v, i}}$ 比较, 得到的差值绝对值小于 ${\rm{\varepsilon }}$ , 则认为推荐成功. 为了提高推荐精度, 在此设定 ${\rm{\varepsilon }} $ =0.1, 如式(14)所示.

$ \left| {{P_{u, v, i}} - {R_{u, i}}} \right| < {\rm{\varepsilon }} $

(14)

用公式 $Correct(u, v, i)$ 表示用户 $u$ 对用户 $v$ 关于项目 $i$ 是否预测成功, 如式(15)所示.

$Correct(u, v, i) = \left\{ {\begin{array}{*{20}{c}} {1\quad \quad \left| {{P_{u, v, i}} - {R_{u, i}}} \right| < {\rm{\varepsilon}} } \\ {0\quad \quad \left| {{P_{u, v, i}} - {R_{u, i}}} \right| > {\rm{\varepsilon}} } \end{array}} \right. $

(15)

设 ${P_u}$ 表示用户 $u$ 为用户 $v$ 推荐的项目集合, 可得到用户 $v$ 对用户 $u$ 的初始信任度 ${T_0}(u, v)$ 如式(16)所示.

$ {T_0}(u, v) = \frac{{\displaystyle \sum\limits_{i \in {P_u}} {Correct(u, v, i)} }}{{\displaystyle \sum {{P_u}} }} $

(16)

以上是通过对项目的预测获取的隐式直接信任度, 下面分析会影响直接信任度的显式因素. 若两个用户对某一个项目的评分都是1, 由于评分范围为1至5, 则可说明这两个用户对这个项目都不感兴趣, 而根据协同过滤算法, 由于这两个用户的评分一致, 会判定有很高的相似性, 事实上只能说明这两个用户不喜欢的项目一致, 并不能说明喜欢的项目一致.

所以在此问题背景下, 再引入兴趣度阈值R, 若两用户u和用户v共同的项目评分值大于等于阈值R, 说明用户u和用户v对这些项目都感兴趣. 若 ${I_{uv}} \geqslant R$ 存在的比例越大, 说明用户的兴趣越相似. 由于评分区间为1至5, 为提高推荐质量, 在此设定阈值R=3.5. 定义兴趣信任度如式(17)所示.

$InterestTrust(u, v) = \frac{{\left| {{I_{uv}} \geqslant R} \right|}}{{{I_{uv}}}}$

(17)

其中, ${I_{uv}}$ 表示用户u和用户v共同评分的项目数, $\left| {{I_{uv}} \geqslant R} \right|$ 表示用户u和v共同评分大于R的项目个数.

综合考虑用户的初始信任度和用户的兴趣信任度, 可得用户u和用户v的直接信任度公式如式(18)所示.

${T_1}(u, v) = InterestTrust(u, v) \times {T_0}(u, v)$

(18)

根据上述方法计算出用户间的直接信任度, 建立信任度矩阵 ${T_1}$ .

(2) 间接信任度

为了改善矩阵稀疏性, 将没有直接信任度的用户连接起来, 需要用到信任度传递. 设用户 $u$ 和用户 $v$ 没有直接信任度, 但用户 $u$ 和用户 ${u_1}$ 有直接信任度, 用户 ${u_1}$ 和用户 $v$ 有直接信任度, 那么就可以说用户 $u$ 和用户 $v$ 通过用户 ${u_1}$ 建立了间接信任关系.

根据小世界思想^[13], 则信任从用户 $u$ 到用户 $v$ 的路经长度超不过6, 由于信任传递路经越长, 得到的信任值越低, 因此设传递中的长度衰减因子 ${\rm{\theta}} $ 如式(19)所示, 其中阈值 $H \leqslant 6$ , 当前路径传递长度为 $N$ .

${\rm{\theta}} = \frac{{H - N + 1}}{H}$

(19)

在一条信任路径中, 会出现许多用户之间不同大小值的信任度. 根据短板理论, 信任度最小的那段传递会拉低整条传递路线的值, 因此将信任度传递中最小的信任度作为整条路径上信任度的重要因素. 若两个用户间的信任度为负数, 则是不信任的, 因此可以终止此条路径上的信任传递. 设 $\mu $ 为信任度阈值, 则用户 $u$ 对用户 $v$ 的间接信任度 ${T_2}(u, v)$ 如式(20)所示, 其中 ${k_1}, \cdots , {k_m}$ 表示中间信任度传递的用户.

$ {T_2}(u, v)\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} min\{ {T_{u, {k_1}}}, \cdots {T_{{k_m}, v}}\} \cdot {\rm{\theta}} , \\ min\{ {T_{u, {k_1}}}, \cdots {T_{{k_m}, v}}\} \cdot {\rm{\theta}} \geqslant \mu \\ \end{array} \\ {0, min\{ {T_{u, {k_1}}}, \cdots {T_{{k_m}, v}}\} \cdot {\rm{\theta}} < \mu } \end{array}} \right. $

(20)

将间接信任度 ${T_2}$ 填充到直接信任度 ${T_1}$ 矩阵中, 构建用户信任度矩阵 $T(u, v)$ .

最后将用户信任度矩阵 $T(u, v)$ 与属性兴趣相似度 $si{m_z}(u, v)$ 结合得到用户特征相似度 $si{m_w}(u, v)$ 如式(21)所示.

$\begin{array}{l} si{m_w}(u, v) = \\ \left\{ {\begin{array}{*{20}{l}} \!\!\!\!{\dfrac{{2\! \times\! si{m_z}(u, v) \!\times \!T\!(u, v)}}{{si{m_z}(u, v) + T(u, v)}}, \;si{m_z}(u, v) \!> \!0, \;T(u, v) \!>\! 0}\!\!\! \\ \!\!\!\!{ T(u, v), \; si{m_z}(u, v) > 0,\; T(u, v) > 0} \\ \!\!\!\!{0, \;T(u, v) > 0} \end{array}} \right. \end{array} $

(21)

2.4 产生推荐

得到用户特征相似度 $si{m_w}(u, v)$ 之后, 选取相似度最高的前 $N$ 个用户, 然后预测目标用户对目标项目的评分, 预测评分公式 ${P_{u, i}}$ 如式(22)所示.

${P_{u, i}} = \overline {{R_u}} + \frac{{\displaystyle \sum\limits_{v \in {N_u}} {si{m_w}(u, v) \times ({R_{v, i}} - \overline {{R_v}} )} }}{{\displaystyle \sum\limits_{v \in {N_u}} {si{m_w}(u, v)} }} $

(22)

其中, ${P_{u, i}}$ 表示目标用户 $u$ 对第 $i$ 个项目的预测评分, ${N_u}$ 表示生成的 $top - N$ 个邻居集合, $\overline {{R_u}} $ 表示目标用户 $u$ 对已评项目的平均评分, $\overline {{R_v}} $ 表示用户 $v$ 对所有已评项目的平均分, ${R_{v, i}}$ 表示用户 $v$ 对第 $i$ 个项目的评分, $si{m_w}(u, v)$ 表示用户特征相似度. 通过上述预测评分公式从大到小排序选取最靠前的 $N$ 个项目作为目标用户 $u$ 的 $top - N$ 个推荐集.

3 实验结果与分析 3.1 实验数据集

为了验证改进算法的有效性, 本实验选取MovieLens站点中的数据集作为实验数据, 它是由美国GroupLens研究小组所建立^[14–16]. 这里采用了MovieLens的100 k数据集, 它是由943个用户对1682部电影的将近100 000个评分所构成, 其中每一个用户都至少要对20部电影进行了评分, 评分区间为1到5. 最终实验根据数据集按80%/20%的比例随机分为训练数据集与测试数据集进行分析比较.

3.2 评价标准

本文实验采用平均绝对误差(MAE)^[17]作为评价标准. MAE越小表明预测越准确、推荐的精度越高. MAE的计算方法如式(23)所示^[18].

$ MAE = \frac{{\displaystyle \sum\limits_{i = 1}^n {\left| {{P_{u, i}} - {R_{u, i}}} \right|} }}{n} $

(23)

3.3 实验结果与分析

实验1. 确定调参的最近邻个数

为了选取合适的最近邻个数以在调参的时候达到较好的推荐结果, 本实验对不同近邻个数的MAE值做分析. 首先选取传统的协同过滤推荐算法, 设定最近邻用户的取值区间为[5, 50], 增量为5, 然后计算MAE, 实验结果如图2所示.

由图2可知, 最近邻用户数的不断增加, MAE值会逐渐降低, 当最近邻用户的值为30时, MAE趋于平稳, 这时的效果比较好, 因此在后面的调参中选取最近邻用户为30.

实验2. 调整用户属性参数

根据式(8), α、β、γ分别表示用户属性中性别、年龄和职业的权重, 通过调整其不同值以达到较好的推荐状态. 根据 ${{\alpha}} + {{\beta}} + {{\gamma}} = 1$ , 设定α、β、γ的取值区间为[0, 1], 增量为0.1, 然后计算不同权重对应的MAE值. 如图3所示, 横坐标为权重 ${\rm{\alpha }}$ 的取值.

由图3可知, 当 ${{\alpha}} =0.5,\;\beta =0.1,\;{{\gamma}} =0.4$ 时, 取得的平均绝对误差(MAE)比其他值都要小, 因此设定 ${{\alpha}} =0.5,\;\beta =0.1,{{\gamma}} =0.4$ 为用户各属性的权重系数.

实验3. 用户属性与皮尔逊相似度的调参

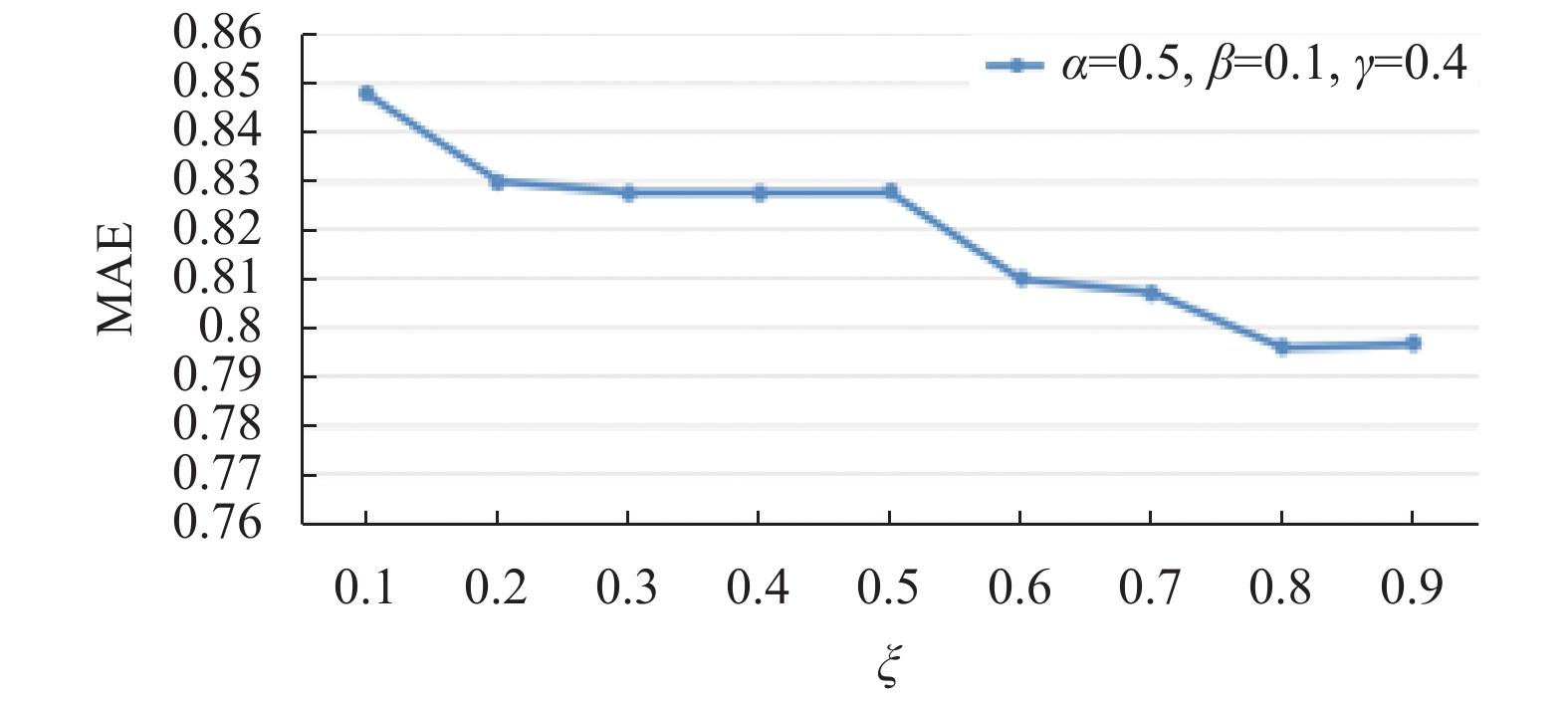
将用户属性相似度与皮尔逊相似度相融合得到用户属性综合相似度 $si{m_p}(u, v)$ . 设权重系数 ${\rm{\xi}} \in [0, 1]$ , 增量为0.1, 然后计算不同权重对应的MAE. 如图4所示, 横坐标为权重 ${\rm{\xi}} $ 的取值.

由图4可知, 当 ${\rm{\xi}} $ =0.8时, 用户属性综合相似度取得的MAE比其他值都要小, 因此设定 ${\rm{\xi}} $ =0.8为用户属性的权重系数.

实验4. 融合兴趣相似度与用户属性相似度

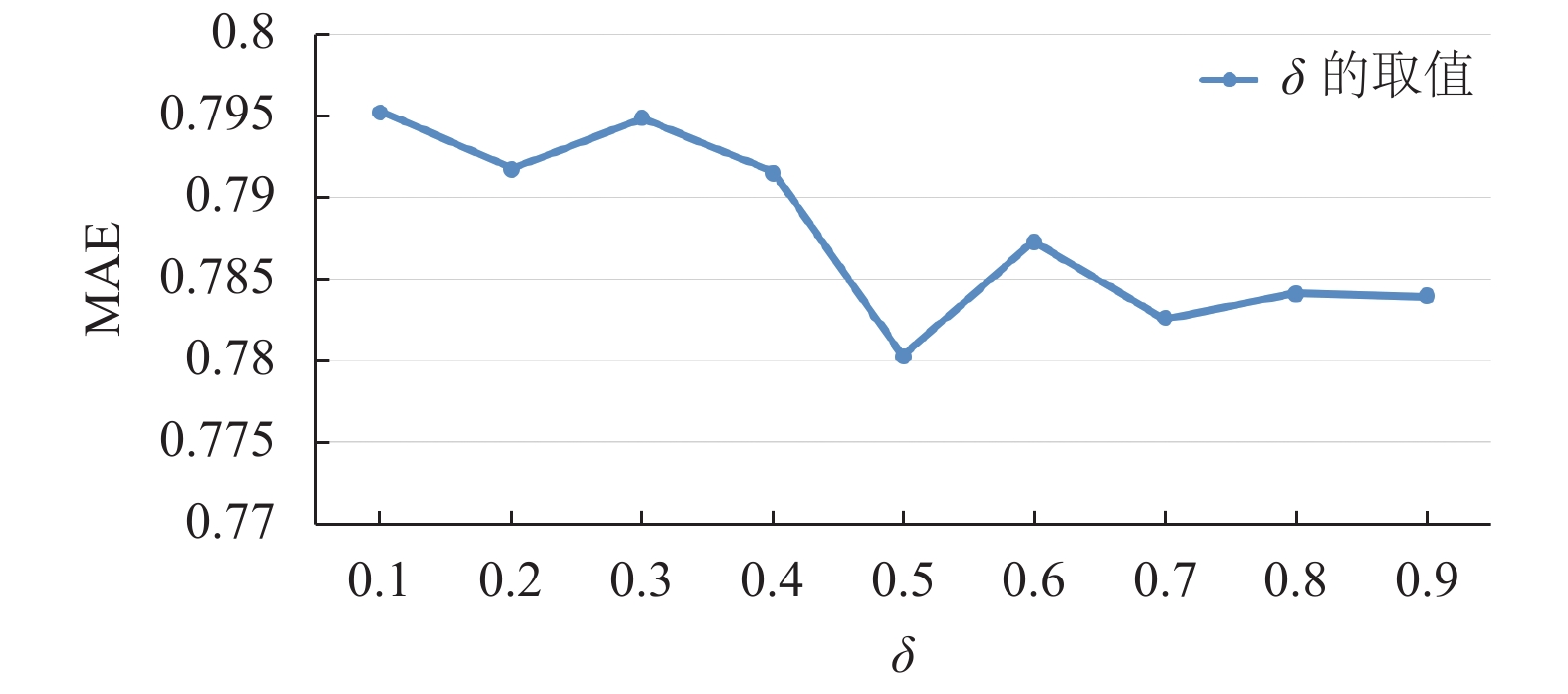
将兴趣相似度和用户属性综合相似度融合得到属性兴趣相似度 $si{m_z}(u, v)$ . 设权重系数 ${\rm{\delta}} \in [0, 1]$ , 增量为0.1, 然后计算不同权重对应的MAE. 如图5所示, 横坐标为权重 ${\rm{\delta}} $ 的取值.

由图5可知, 当 ${\rm{\delta}} $ =0.5时, 属性兴趣相似度取得的MAE比其他值都要小, 因此设定 ${\rm{\delta}} $ =0.5为属性兴趣相似度的权重系数.

实验5. 确定信任度传递的阈值

如果在两用户间信任度很低时再进行信任度传递, 会造成推荐结果的失真. 对于这种情况, 本文设定信任度阈值为 ${\rm{\mu}} \in [0, 1]$ , 增量为0.1, 然后计算不同阈值 ${\rm{\mu}} $ 对应的MAE. 如图6所示, 横坐标为权重 ${\rm{\mu}} $ 的取值.

由图6可知, 当阈值 ${\rm{\mu}} $ =0.8时, 间接信任相似度取得的MAE比其他值都要小, 因此当 ${\rm{\mu}} $ =0.8时进行信任度的传递.

实验6 不同推荐算法的对比实验

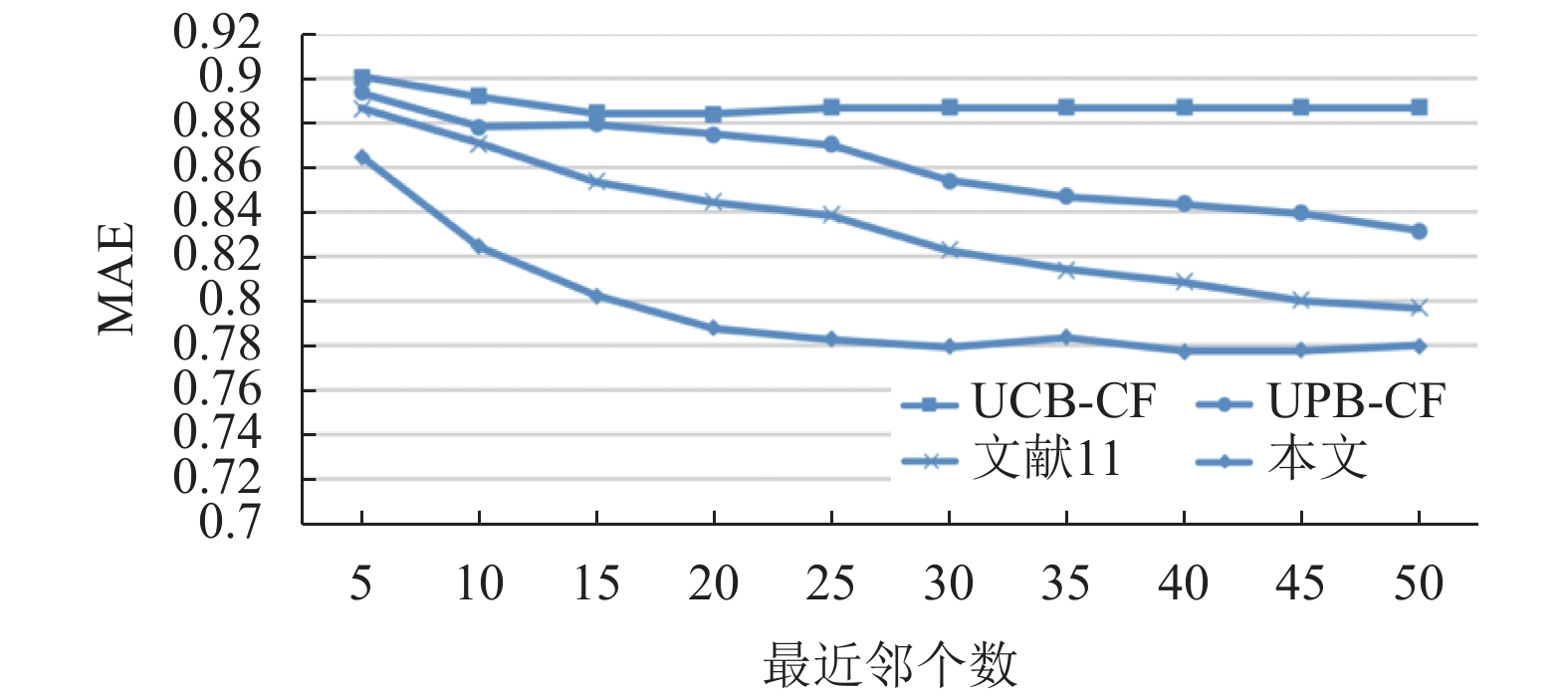
本实验选取传统的基于余弦相似性的协同过滤算法(UCB-CF)、基于皮尔逊相似性的协同过滤算法(UPB-CF)、文献[11]提出的用户特征的协同过滤算法和本文提出的基于用户特征的协同过滤算法做对比, 四种方法的最近邻用户取值区间均为[5, 50], 增量为5, 则MAE的结果如图7所示.

由图7可知, 当用户最近邻个数在[5, 50]之间变化时, 四种推荐算法的MAE都逐渐下降, 但本文提出的基于用户特征的协同过滤算法在融合用户属性、兴趣度和信任度之后, 得到的平均绝对误差都比其他三种算法要小, 推荐质量要好.

4 结论与展望

通过分析传统协同过滤算法的问题, 本文综合考虑提出了一种融合用户属性、用户兴趣度和信任度的基于用户特征的协同过滤推荐算法. 通过分析对比实验证明, 本文提出的算法在一定程度上能改善新用户的冷启动、数据稀疏性和推荐准确性等问题, 有效的提高了推荐质量. 接下来的工作还要研究用户兴趣随时间变化对兴趣度的影响, 此外, 如何获取信任模型中更好的传递规则也是需要继续深入研究的课题.