2. 湖南软件职业学院 软件与信息工程学院, 湘潭 411100
2. School of Software and Information Engineering, Hunan Software Vocational Institute, Xiangtan 411100, China
边缘是像素灰度值发生剧烈变化的像素的集合, 图像大部分的信息存在于边缘中. 边缘检测是图像处理领域中研究最广泛最重要的课题之一, 也是图像分割、图像重建、特征提取和目标识别的基础.
当从图像中提取边缘时, 通常会出现一些错误, 比如曲线不连接、缺失边缘和假边. 因此, 构建一种能够精确检测图像边缘的方法是至关重要的. 目前为止, 已经有许多不同的方法成功的应用到图像边缘检测中[1–6]. 文献[1]提出一种在边缘检测过程中加入边缘曲度算子进行噪声衰减的边缘检测方法. 此方法可以抑制噪声得到较高的定位精度, 但耗时比传统Canny方法有一定的增加. 文献[2]是采用小波变换和改进的自适应中值滤波器代替Canny方法中使用的高斯滤波器对图像进行平滑处理, 具有较高的定位精度, 但时间复杂性有所增加. 文献[3]提出了一种基于灰度关联的自适应边缘检测方法, 该方法可以自适应的计算阈值, 使边缘更加完整, 但有时没有设置阈值精度高. 文献[4]提出了一种基于估计理论的边缘检测方法, 该方法在局部细节上具有一定的优势, 但检测完整性不具有优势. 文献[5]提出一种Canny算子与智能路由算法相结合的边缘检测方法, 该方法对边缘映射效果要求很高. 文献[6]提出一种基于多级形态学的模糊边缘检测方法, 该方法可以得到较准确的边缘检测结果, 此方法适用于有多目标而不是单一目标.
目前已有的边缘检测方法除了对传统边缘检测算子进行改进之外, 随着人工智能的发展, 又出现一些新的边缘检测方法[7–10].
传统边缘检测方法包括Roberts, Sobel, Prewitt, Laplace, LOG和Canny等方法, 有很多研究人员在此基础上继续研究[11–19]. Roberts算子、Sobel算子、Prewitt算子属于一阶微分算子, 一阶微分算子在图像边缘提取过程中均会产生比较宽的边缘响应, 需要进一步细化边缘, 而且对噪声比较敏感. Laplace算子、LOG算子属于二阶微分算子, 对边缘点有很好的定位能力, 但抗噪能力也不是很高. 在这几种边缘检测方法中, Canny边缘检测方法比其他边缘检测方法性能更好[15,16]. Canny方法通过使用高斯滤波器对图像进行光滑处理来提高抑制噪声的能力, 但也很容易丢失一些细节.
从数学角度分析, 微分要求函数曲线具有一定的光滑度, 但积分对函数曲线的光滑度要求不高. 因此, 本文从积分的角度, 提出一种基于局部能量的边缘检测方法. 此方法是在以一个像素点为中心的对称区域中, 计算区域内所有像素的灰度值与中心像素的灰度值之间的差值, 差值平方的总和作为中心像素点所对应的局部能量. 这个局部能量是一种积分形式的. 通过局部能量的大小来判断此积分区域内是否存在边缘. 一般地, 边缘点对应的局部能量较大, 而光滑区域内的像素点对应的局部能量是比较小的. 因此, 根据局部能量函数的大小, 就可以快速有效地找到边缘点所在的位置.
1 基于局部能量的边缘检测方法 1.1 局部能量方法图1(a)是一个理想的阶跃曲线, 灰度值的跃变表明图像中边缘点的存在. 图1(b)是阶跃曲线的导数. 图1(b)中的峰值点对应图像的边缘点. 如图2所示, 假设有一条线段L, 长度是2r, 线段的中心点是x. 让线段L的中心点沿着曲线移动. 运动过程如图2所示. 中心点x在曲线上移动过程中相对应点的像素灰度值都称为f(x), 而线段与曲线所围对称区域内所有像素点构成一个集合, 像素点

|
图 1 阶跃曲线及其导数 |

|
图 2 水平线段L的中心点沿曲线运动时, 曲线与水平线段L的中点的差值示意图 |
根据以上的分析, 局部能量函数定义如下:
| $E\left( x \right) = {\int_{{\Omega _x}} {\left( {f\left( y \right) - f\left( x \right)} \right)} ^2}dy$ | (1) |
考虑到高斯核函数K(x)具有紧支撑性和加权的特性, 式(1)可以改写成:
| $E\left( x \right) = {\int_{{\Omega _x}} {K\left( {x - y} \right)\left( {f\left( y \right) - f\left( x \right)} \right)} ^2}dy$ | (2) |
本文选择的高斯核函数是式(3).
| $ K(x) = \frac{1}{{\sqrt {2\pi } }}{e^{ - \frac{{{x^2}}}{2}}} $ | (3) |
基于上述对图2的分析, 可以得到如下的结论:
结论: 线段L的中心点沿着曲线移动, 局部能量值是不断变化的, 当线段的中心点与边缘点重合时, 局部能量达到最大值.
证明. 在图2中, 局部能量函数在边缘点x=0处达到最大值.
| $ \begin{split} E(x) = &{\int_{{\Omega _x}} {K(x - y)(f(y) - f(x))} ^2}dy \\ = &{\int_{x - r}^{x + r} {K(x - y)(f(y) - f(x))} ^2}dy \\ \end{split} $ | (4) |
假设
| $ \begin{split} E(x) = &\int_r^{ - r} { - K(\tau ){{(f(x - \tau ) - f(x))}^2}} d\tau \\ =& \int_0^r {K(\tau )(({f^2}(x + \tau ) + ({f^2}(x - \tau ))}\\ &- 2f(x)(f(x + \tau ) + f(x - \tau )) + 2{f^2}(x))d\tau \end{split} $ | (5) |
对式(5)求导数得:
| $\begin{split} E'(x) =& 2\int_0^r {K(\tau )} ((f(x + \tau )f'(x + \tau ))\\ & -(f(x - \tau )f'(x - \tau ){\rm{))d}}\tau\\ &- 2\int_0^r {K(\tau )} (f'(x)(f(x + \tau ) - f(x - \tau ))\\ & + f(x)(f'(x + \tau ) + f'(x - \tau )))d\tau\\ & +4\int_0^r {K(\tau )} f(x)f'(x)d\tau\\ = & {\rm{2}}\int_0^r {K(\tau )} ((f(x + \tau ) - f(x))(f'(x + \tau ) - f'(x)) \\ & +(f(x) - f(x - \tau ))(f'(x) - f'(x - \tau )))d\tau \\ \end{split} $ | (6) |
当x=0时
| $\begin{split} E'(0) =& 2\int_0^r {K(\tau )} ((f(\tau ) - f(0))(f'(\tau ) - f'(0))\\ &+ (f(0) - f( - \tau ))(f'(0) - f'( - \tau )))d\tau\\ = & 2\int_0^r {K(\tau )} (f(\tau )(f'(\tau ) - f'(0))\\ & +f(\tau )(f'(0) - f'( - \tau )))d\tau\\ = & 0 \end{split} $ | (7) |
如图1所示, 函数f(x)是奇函数, f(x)的导数是偶函数.
因为,
(1)当
(2)当
综上所述, 只要满足x>0,E′(x)的值是恒小于零的, 因此, 当x>0时局部能量函数E(x)是一个单调递减函数.
同样的, 根据f′(x)的对称性, 当x<0时, 局部能量函数E(x)是单调递增函数. 因此, 局部能量函数在边缘点x=0取得大值. 在实验中, 我们通过调整阈值得到边缘点.
例如, 如图3(a)所示, x=0处的跳变点为边缘点. 如图3(b)所示, 局部能量最大值点也在x=0处.

|
图 3 阶跃曲线及其各点对应的局部能量示意图 |
本文提出了一种基于局部能量的边缘检测方法, 当中心点位于对称区域中的光滑区域时, 局部能量值比较小, 当位于边缘点时, 局部能量达到最大值. 因此, 可以通过局部能量的最大值来快速准确的确定边缘点位置.
本文方法的算法步骤如下:
步骤1. 输入图像;
步骤2. 使用高斯核函数对图像进行预处理;
步骤3. 边缘检测响应采用式(2)的局部能量函数;
步骤4. 选择适当的阈值进行处理;
步骤5. 输出边缘映射图.
2 数值实验在本节中, 通过一系列的实验验证了该方法的有效性. 实验中使用的图像包括正常图像、合成图像、医学图像以及Berkeley分割数据集(BSDS)中图像. 本节分两部分进行实验: 1) 与常用边缘检测方法的对比; 2) 通过Baddeley误差度量(BEM)[20]方法进行的数值比较.
2.1 与常用边缘检测方法对比实验本文方法与常用边缘检测方法对合成图像和医学图像的边缘检测结果对比如图4、图5、图6所示.
|
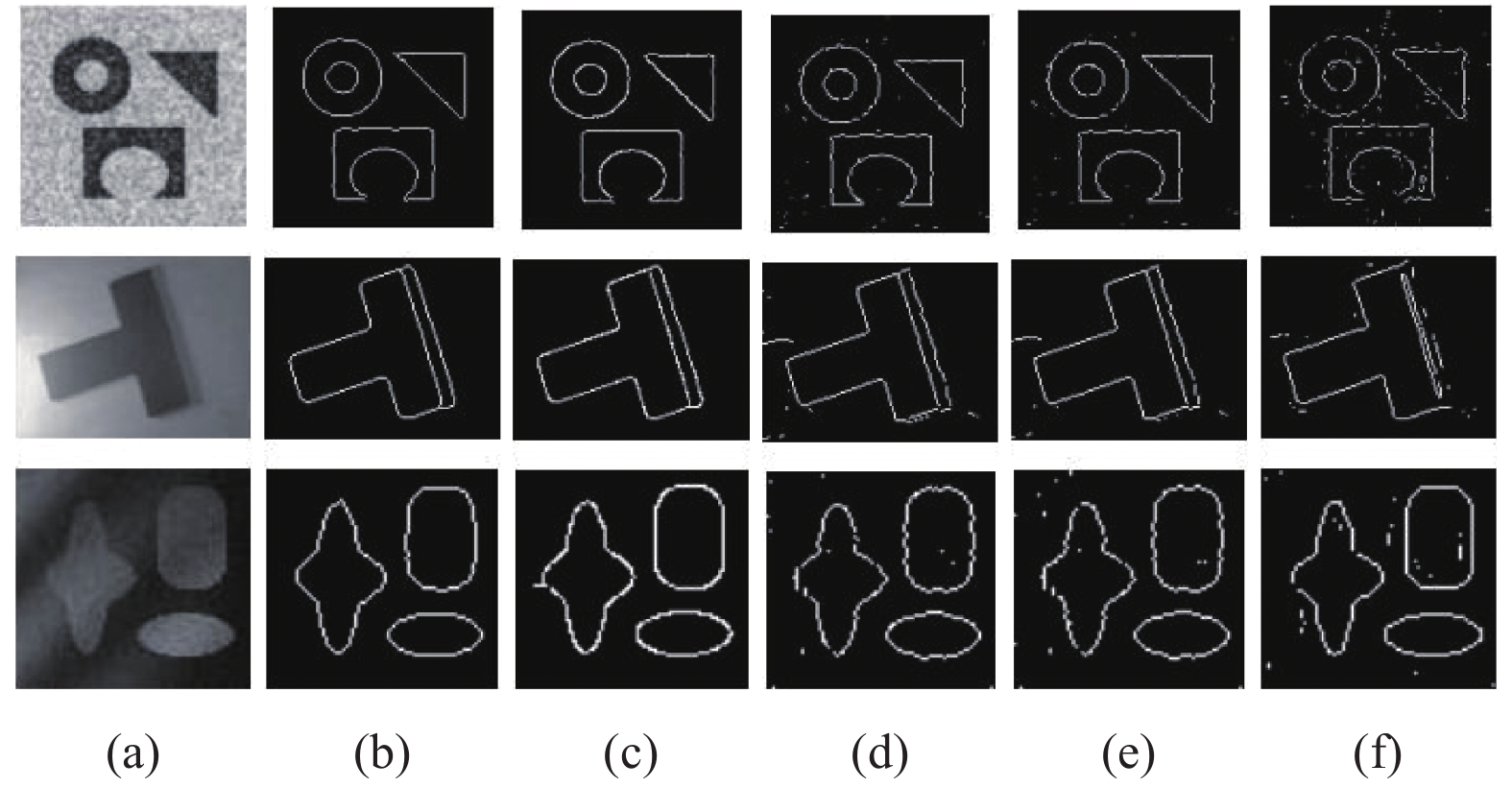
图 4 本文方法与常用边缘检测方法对合成图像的边缘检测结果示意图(括号中数值为从上到下阈值). (a)原图; (b) 本文方法(0.4, 0.15, 0.27); (c) Canny (0.8, 0.35, 0.45); (d) Sobel (30, 5, 9); (e) Prewitt (30, 5, 8); (f) LoG (3, 0.5, 0.7) |
其中, 图4和图5的第(a)列是原图, 第(b)–(f)列分别是采用本文方法、Canny方法、Sobel方法、Prewitt方法和LoG方法的边缘检测结果. 从图片效果上看, 本文方法的检测结果要优于其它方法.
图6的第二行图像是在第一行原图的基础上加了标准差为0.05的高斯噪声图像, 第四行图像是在第三行原图的基础上加了标准差为0.1的高斯噪声图像. 实验结果表明, 本文方法能得到更好的检测结果.
图7为本文方法与其他文献所提方法的比较, 从实验结果来看, 本文方法能得到较好的边缘检测结果.

|
图 5 本文方法与常用边缘检测方法对医学图像的边缘检测结果示意图(括号中数值为从上到下阈值). (a)原图; (b)本文方法(0.25, 0.26); (c)Canny (0.3, 0.45); (d) Sobel (17, 5); (e) Prewitt(12, 5); (f) LoG (0.2, 0.4) |

|
图 6 本文方法与常用边缘检测方法对原图与添加了高斯噪声图像的边缘检测结果示意图(括号中数值为从上到下阈值). (a)原图; (b)本文方法(0.19, 0.19, 0.2, 0.3); (c) Canny (0.19, 0.17, 0.3, 0.5); (d) Sobel (15, 19, 15, 30); (e) Prewitt (15, 18, 15, 30); (f) LoG (1.5, 1.5, 1.2, 1.8) |

|
图 7 本文方法与其他文献检测方法的对比 |
2.2 BEM对比试验
在本节中, 通过对不同条件下的相同图像进行实验来比较本文方法和其他方法. 为了进行定量比较, 本文使用 Baddeley误差度量(BEM)[20]方法进行实验验证. 两个二进制图像的不同之处是由BEM计算的. 这些实验是在不同类型的Berkeley分割数据集(BSDS)[21,22]图像上进行的. 在本节实验中使用了很多不同场景下的图像.
因为边缘映射图像通常是以二进制的形式显示, 因此, 它可以使用BEM方法进行比较研究.
| ${\Delta ^k}({I_1}, {I_2}) = {\left[\frac{1}{{\left| p \right|}}{\sum\nolimits_{p \in P} {\left| {\omega \left(d\left(p, {I_1}\right)\right) - \omega \left(d\left(p, {I_2}\right)\right)} \right|} ^k}\right]^{{1 / k}}}$ | (8) |
其中,
BEM方法是用来比较两幅二进制图像之间的差异性的. 所以, 通过BEM方法得到的实验结果越小, 说明两幅图像间的差异性越小, 也就意味着边缘检测得到的结果越接近BSDS数据库中给出的真实边缘图像.
将本文方法和其他方法应用到Berkeley分割数据集(BSDS)的10个测试图像中, 把不同方法得到的二进制图像与BSDS中给出的真实边缘图像使用BEM方法计算不同之处, 并将本文方法与其他方法得到的实验结果进行比较. 实验中用到的图像分为两类: 原图像和添加高斯噪声图像.
使用边缘检测方法来处理图像时, 选择不同的阈值进行实验, 通过对阈值大小的不断调整, 选择一个最接近实际边缘的二进制图像进行比较. 这样得到的实验结果是比较合理的.
| 表 1 本文方法与其他方法对原图使用BEM方法得到的实验结果 |
表1为采用本文方法与其他算法针对原图进行边缘检测的BEM值对照表. 表1中第一列为BSDS数据库中的图像编号, 第2–9列分别为Canny0.75、Canny1.5、Prewitt、Sobel、LoG、Ant算法[23]、GED-T[24]、GED-EA[25]和本文方法的BEM值(其中, Canny0.75表示Canny方法采用阈值为0.75的情形). 表1中的最后一行的sum项为各种方法处理数据库图例的各项BEM值的总和. 从表1可以看出, 本文方法的检测结果中至少有6幅图像的结果是优于其他几种方法方法. 例如, BSDS数据库中图像编号为69015的图像, 本文方法的BEM值比其他几种方法的BEM值都要小, 也就是说, 本文方法与其他几种边缘检测方法相比, 边缘检测得到的结果更接近BSDS数据库中给出的真实边缘图像. 但也有几幅图像的实验结果并不都是最小的, 如图像编号为54082的图像, 本文方法检测到的结果并不是最好的, 但与其他方法相比也是可以接受的, 而且表1中所有图例的BEM总和也是最小的.
表2为采用本文方法与其他算法针对添加噪声的图像进行边缘检测的BEM值对照表. 噪声图像是在原图像的基础上, 添加了标准差为0.1的高斯噪声得到的. 表2中的数据显示, 本文方法针对含噪声图像的边缘检测结果中至少有6幅图像的结果是比其他几种方法得到的结果都要小, 说明针对噪声图像, 本文方法得到的检测结果也是比较接近BSDS数据库中给出的真实边缘图像. 因此, 本文方法对含有少量噪声的图像的边缘检测也是有效的.
| 表 2 本文方法与其他方法在添加噪声的图像中使用BEM方法得到的实验结果 |
表1和表2给出的数据中, 本文方法无论是对原图还是对添加了高斯噪声后的图像的检测结果都有超过半数是比其他方法检测到的数值要小. 根据BEM方法的理论知, 数值越小, 检测到的结果越接近数据库中给出的边缘图, 说明检测结果的准确性越高. 因此, 本文方法的优势在于检测结果相对于其他几种方法来说是比较好的.
3 结论本文提出了一种新的基于局部能量的图像边缘检测方法. 局部能量最大的点对应于边缘点. 通过局部能量, 可以有效地找到边缘点. 通过大量的实验验证, 本文方法无论是从视觉效果上还是BEM定量结果上, 与其他方法相比, 都能得到比较好的检测结果.
| [1] |
郑子华, 陈家祯, 叶锋. 基于曲率估计的Canny边缘检测算法. 计算机系统应用, 2017, 26(12): 148-154. DOI:10.15888/j.cnki.csa.006139 |
| [2] |
李俊山, 马颖, 赵方舟, 等. 改进的Canny图像边缘检测算法. 光子学报, 2011, 40(S1): 50-54. |
| [3] |
Qiao BM, Jin L, Yang YF. An adaptive algorithm for grey image edge detection based on grey correlation analysis. Proceedings of the 12th International Conference on Computational Intelligence and Security (CIS). Wuxi, China. 2016. 470–474.
|
| [4] |
Borse S, Bora PK. A novel approach to image edge detection using Kalman filtering. Proceedings of the 7th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON). Vancouver, BC, Canada. 2016. 1–5.
|
| [5] |
Akinlar C, Chome E. CannySR: Using smart routing of edge drawing to convert Canny binary edge maps to edge segments. Proceedings of 2015 International Symposium on Innovations in Intelligent Systems and Applications (INISTA). Madrid, Spain. 2015. 1–6.
|
| [6] |
Perumal E, Arulandhu P. Multilevel morphological fuzzy edge detection for color images (MMFED). Proceedings of 2017 International Conference on Electrical, Electronics, Communication, Computer, and Optimization Techniques (ICEECCOT). Mysuru, India. 2017. 269–273.
|
| [7] |
Azeroual A, Afdel K. Fast image edge detection based on Faber Schauder wavelet and Otsu threshold. Heliyon, 2017, 3(12): e00485. DOI:10.1016/j.heliyon.2017.e00485 |
| [8] |
Kim J, Chun CY, Cho BH. Evaluation of noise reduction in experimental battery pack voltage using discrete wavelet transform and wavelet packet transform. Proceedings of 2015 IEEE International Telecommunications Energy Conference (INTELEC). Osaka, Japan. 2015. 1–5.
|
| [9] |
Li XF, Zhang YH. Digital image edge detection based on LVQ neural network. Proceedings of the 11th Conference on Industrial Electronics and Applications (ICIEA). Hefei, China. 2016. 1251–1255.
|
| [10] |
Jin RJ, Yin JJ, Zhou W, et al. Improved multiscale edge detection method for polarimetric SAR images. IEEE Geoscience and Remote Sensing Letters, 2016, 13(8): 1104-1108. DOI:10.1109/LGRS.2016.2569534 |
| [11] |
Rosenfeld A. The max Roberts operator is a hueckel-type edge detector. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1981, PAMI-3(1): 101-103. DOI:10.1109/TPAMI.1981.4767056 |
| [12] |
Gonzalez CI, Melin P, Castro JR, et al. An improved sobel edge detection method based on generalized type-2 fuzzy logic. Soft Computing, 2016, 20(2): 773-784. DOI:10.1007/s00500-014-1541-0 |
| [13] |
Nguyen PML, Cho JH, Cho SB. An architecture for real-time hardware co-simulation of edge detection in image processing using Prewitt edge operator. Proceedings of 2014 International Conference on Electronics, Information and Communications (ICEIC). Kota Kinabalu, Malaysia. 2014. 1–2.
|
| [14] |
Wang X. Laplacian operator-based edge detectors. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(5): 886-890. DOI:10.1109/TPAMI.2007.1027 |
| [15] |
Singh R, Vashisht M, Qamar S. Role of linguistic quantifier and digitally approximated Laplace operator in infrared based ship detection. International Journal of System Assurance Engineering and Management, 2017, 8(S2): 1336-1342. DOI:10.1007/s13198-017-0604-x |
| [16] |
Mallick A, Roy S, Chaudhuri SS, et al. Optimization of Laplace of Gaussian (LoG) filter for enhanced edge detection: A new approach. Proceedings of 2014 International Conference on Control, Instrumentation, Energy and Communication (CIEC). Calcutta, India. 2014. 658–661.
|
| [17] |
Biswas R, Sil J. An improved canny edge detection algorithm based on type-2 fuzzy sets. Procedia Technology, 2012, 4: 820-824. DOI:10.1016/j.protcy.2012.05.134 |
| [18] |
Sangeetha D, Deepa P. FPGA implementation of cost-effective robust Canny edge detection algorithm. Journal of Real-Time Image Processing, 2016, 1-14. DOI:10.1007/s11554-016-0582-2 |
| [19] |
Kelefouras V, Kritikakou A, Goutis C. A methodology for speeding up edge and line detection algorithms focusing on memory architecture utilization. The Journal of Supercomputing, 2014, 68(1): 459-487. DOI:10.1007/s11227-013-1049-x |
| [20] |
Baddeley AJ. An error metric for binary images. Proceedings of International Workshop on Robust Computer Vision: Quality of Vision Algorithms. Karlsruhe. 1992. 59–78.
|
| [21] |
Martin D, Fowlkes C, Tal D, et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. Proceedings of the Eighth IEEE International Conference on Computer Vision. Vancouver, BC, Canada. 2001. 416–423.
|
| [22] |
Martin DR, Fowlkes CC, Malik J. Learning to detect natural image boundaries using local brightness, color, and texture cues. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(5): 530-549. DOI:10.1109/TPAMI.2004.1273918 |
| [23] |
Nezamabadi-pour H, Saryazdi S, Rashedi E. Edge detection using ant algorithms. Soft Computing, 2006, 10(7): 623-628. DOI:10.1007/s00500-005-0511-y |
| [24] |
Lopez-Molina C, Bustince H, Fernandez J, et al. A gravitational approach to edge detection based on triangular norms. Pattern Recognition, 2010, 43(11): 3730-3741. DOI:10.1016/j.patcog.2010.05.035 |
| [25] |
Deregeh F, Nezamabadi-pour H. A new gravitational image edge detection method using edge explorer agents. Natural Computing, 2014, 13(1): 65-78. DOI:10.1007/s11047-013-9382-9 |
 2019, Vol. 28
2019, Vol. 28



