1 引言

作为一种重要的降维技术, 特征选择是一个热门的研究课题, 现有的特征选择方法可以分为两大类:过滤法和封装法. 过滤法先对数据集进行特征选择, 然后再训练学习器, 特征选择过程与后续学习器无关. 与过滤法不同, 封装法直接把最终要使用的学习器的性能作为特征子集的评价准则. 换言之, 封装法的目的就是为给定的学习器选择最有利于其性能的特征子集. 封装法的性能常依赖于具体的分类器, 而过滤法的性能通常无此依赖性, 由于过滤法的较好适应性, 相比封装法, 过滤法得到了更多的关注.

Relief是一种广泛应用的过滤型方法, 在文献[1]中首次被提出用于二类数据的特征选择, 虽然Relief算法比较简单, 运行效率高, 并且结果也比较令人满意, 但是其局限性在于只能处理二类数据, Kononenko将其扩展到多类情况, 提出ReliefF算法, 并在文献[2]中对ReliefF算法做了深入探讨. 虽然Relief已经得到较广泛的应用, 但它依然存在一些不足之处^[3], 例如, 该类算法的数学形式依然没有得到很好的定义, 故它的特点和性质还难以得到深入的研究, 此外, 它依然缺乏强大的处理异常数据点的机制, 以及需要提高在噪音环境下的鲁棒性. 目前, 已有许多改进Relief算法的文献, 如迭代Relief算法I-RELIEF^[4], I-RELIEF算法基于间隔最大化构造优化目标函数, 并以类EM算法的迭代策略来导出权重向量的学习规则. 另外, 文献[5]中提出了类依赖特征权重Relief算法, 由于不同类别数据点的各个特征重要性可能存在很大不同, 类依赖特征权重Relief算法为每个类别数据点单独训练一个权重, 以克服使用全局权重时不同类别数据点间特征重要性不同带来的影响.

另外, 已有许多结合实例选择和特征选择的研究. 有研究通过进化计算同时进行实例和特征选择以及加权^[6], 提出了组合这四项任务的一般框架, 并对15种可能的组合的有用性进行了全面研究. 还有基于动态不完整数据粗糙集的增量特征选择^[7], 提出了一种增量的特征选择方法, 可以加速动态不完整数据中的特征选择过程. 还有研究提出结合实例选择的三种策略进行基于实例的学习^[8], 首先, 它使用CHC遗传算法的框架. 其次, 它包含了多次选择每个实例的可能性. 最后, 它使用的本地k值取决于每个测试实例的最近邻居, 这三种组合策略能够比以前的方法实现更好的减少, 同时保持与k近邻规则相同的分类性能. 目前已经有多个实例加权方案用于改进Relief算法的准确率, 如Iterative Relief, I-RELIEF, 和SWRF, 这些方法应用不同的实例加权方案并且有不错的效果.

为了克服类依赖特征权重的不足, 提高类依赖特征权重Relief算法准确率. 本文从局部特征权重数据分类的角度修改权重训练过程并引入实例权重来提高对边界点的敏感性. 本文第2部分先介绍Relief和类依赖Relief, 并分析类依赖Relief的不足之处, 第3部分提出本文算法, 第4部分采用8个UCI数据集进行实验. 第5部分对文章内容进行总结.

2 Relief和类依赖Relief

Relief算法中使用全局权重, 但是因为全局距离度量使用的特征权重没有区别不同的类别, 所以当一些特征对于不同的类表现得不同时会导致分类性能不佳. 相比全局权重, 局部特征权重更能反映不同类中相同特征的不同重要性, 因此, CDRELIEF通过学习局部权重来提高权重关于类别的相关性, 目前, 已有许多方法^[9,10]用于在局部区域上学习距离度量, 也有局部和全局相结合的距离度量^[11]. 对于不同的类别来说特征权重是不一样的. 最有代表性的方法是类依赖加权距离度量(CDW), 该距离与原型的类标签相关:

$ {d_{CDW}}(x,y) = \sqrt {\sum\limits_{j = 1}^D {w_{c,j}^2{{({x_j} - {y_j})}^2}} } $

(1)

式中 ${d_{CDW}}\left( {x,y} \right)$ 是点x和点y的类依赖加权距离, D表示数据维度, c是点x的类标签, ${w_{c,j}}$ 表示类别c第j个特征的权重.

2.1 Relief

Relief特征加权^[1]的核心思想是根据每一个特征区分不同类实例的能力来估计特征权值及其重要性, 给定一个包含N个实例的二类数据集X, C是类标签集合, x是X中的一个实例, 每个实例 $x = ({x_1},{x_2}, \cdots, {x_D})$ 是一个维度为D的实值向量. Relief进行如下迭代学习: 随机的选取一个实例x, 然后寻找同类最近实例 $NH\left( x \right)$ 和异类最近实例 $NM\left( x \right)$ , 接着利用如下规则更新权值:

$ {w_j} = {w_j} + \frac{1}{T} \cdot |{x_j} - NM{(x)_j}| - \frac{1}{T}|{x_j} - NH{(x)_j}| $

(2)

其中, $\left| {{x_j} - {y_j}} \right|$ 是用来计算两个实例第j维特征值的差异程度, 即特征差值向量的绝对值向量. 具体地, Relief算法如算法1所示.

算法1. Relief算法

① 给定一个包含N个实例和D个特征的二类数据集X, 设置初始权值 ${w_j} = 0\;(1 \le j \le D)$ 以及最大迭代次数T, 并且设置迭代初始值t=1.

② 从数据集X中随机选取一个实例x并计算该实例的同类最近实例 $NH\left( x \right)$ 和异类最近实例 $NM\left( x \right)$ .

③ 对于每一维权值, 利用式(2)更新权值.

④ 若t=T, 算法结束, 否则t=t+1返回步骤②.

⑤ 输出更新以后的权值向量w.

从最近邻居Relief发展出了考虑K个邻居的变体, 它的权重更新公式为:

$ \begin{aligned} {w_j} = & {w_j} + \sum\nolimits_{z \in KNN(x,l),l \ne c} {|{x_j} - {z_j}|/T } \\ & - {\sum\nolimits_{z \in KNN(x,c)} {|{x_j} - {z_j}|} } /T \end{aligned} $

(3)

$KNN(x,c)$ 是x在 ${X_c}$ 中通过欧氏距离求得的K个最近邻居的集合.

2.2 类依赖Relief

Elena Marchiori^[5]研究将Relief分解为类依赖特征权重, 并表示使用全局特征权重时将同一特征在不同类中的权重相加会抵消彼此关于单个类别的相关性, 导致特征关于单个类别的相关性可能不会被检测到, 因此他们提出将原来的所有数据共用一个特征权重改为一个类别一个特征权重, 类c的特征权重为 ${w_c}$ , 这样可以保留特征关于单个类别的相关性. 计算类别权重 ${w_c}$ 时只选取类别为c的实例x, 然后找该实例邻居, 对类别权重进行更新. 权重更新公式为:

$ {w_c} = \sum\nolimits_{x \in {X_c}} {\sum\nolimits_{z \in KNN(x,c)} { - |x - z|} /T + \sum\nolimits_{z \in \mathop {KNN}\limits_{l \ne c} (x,l)} {|x - z|} } /T $

(4)

${w_c}$ 被看做类别c的特征权重, ${X_c}$ 是类别为c的数据点集合, $KNN\left( {x,c} \right)$ 是x的同标签k近邻, $\mathop {KNN}\limits_{l \ne c} (x,l)$ 是x的标签不为c的k近邻. 根据式(4)可以为数据集中每个类别数据求得一个特征权重.

3 实例加权类依赖Relief

然而, 存在如下问题:在训练权重 ${w_c}$ 过程中, 对属于类c的数据点 ${x^1}$ 和不属于类c的数据点 ${x^2}$ , 目的是使 ${x^1}$ 和 ${x^2}$ 在 ${w_c}$ 下的加权距离比 ${x^1}$ 和同属于类c的数据点 ${x^3}$ 在 ${w_c}$ 下的加权距离要大. 即 $||{x^1} - {x^2}|{|_{{w_c}}} \ge ||{x^1} - {x^3}|{|_{{w_c}}}$ .

但是在分类过程中, 与权重训练过程中使不同类数据点在同一个权重下比较距离大小的思想不同, 现有一个属于类别c的数据点 ${x^1}$ , 一个属于类别l的数据点 ${x^2}$ . 要正确分类一个属于类c的数据点y, 需要满足条件: $||y - {x^2}|{|_{{w_l}}} \ge ||y - {x^1}|{|_{{w_c}}}$ , 即点y与点 ${x^2}$ 在 ${w_l}$ 下的加权距离要比y与点 ${x^1}$ 在 ${w_c}$ 下的加权距离要大. 点y和类c数据点 ${x^1}$ 间的距离用 ${w_c}$ 计算, $d(y,{x^1}) = ||y - {x^1}|{|_{{w_c}}}$ 和类l数据点 ${x^2}$ 的距离用 ${w_l}$ 计算, $d(y,{x^2}) = ||y - {x^2}|{|_{{w_l}}}$ . 另外, 为了提高训练出的特征权重的分类精度, 本文将参与权重训练的实例限制在分类边界附近的点.

3.1 实例权重

本文中设置实例权重是一方面由于难分类的点是位于类边界的点, 那些远离类边界的点不容易分类错误. 当类边界处的点能够正确分类时远离类边界的点也能分类正确. 另一方面由于远离类边界的点在参与特征权重更新公式中对特征权重值造成的变化量较大, 而类边界处点对特征权重值造成的变化量较小, 因此远离类边界点的参与容易使得训练出的分类边界不能够正确分类类边界点. 因此只需要选取类边界附近的点参与分类边界的确定, 从而避免了远离类边界的点对特征权重的影响, 进而提高了分类准确率.

在权重更新过程中通过令远离类边界的数据点实例权重值为0, 来排除远离类边界的数据点对特征权重更新的影响, 同时也排除了离群点的影响, 进而提高训练出的特征权重具有更高的分类精度. 实例权重公式如下:

$ IW(x) = \left\{ {\begin{array}{*{20}{c}} {1,\;\quad {\rm{if}}(\;\min ({d_1}/{d_2},{d_2}/{d_1})\; > threshold)}\\ {0,\,\quad {\rm{if}}(\;\min ({d_1}/{d_2},{d_2}/{d_1})\; < threshold)} \end{array}} \right. $

(5)

其中, threshold是设定的阈值, 取值为0到1之间的值. d₁是x到k个同类邻居的距离和, d₂是x到k个异类邻居的距离和, 如果当前实例到同类邻居的距离之和d₁与到异类邻居的距离之和d₂的比值 ${d_1}/{d_2} < threshold$ 说明当前实例点远离类边界, 实例点权重设为0, 从而不影响特征权重更新. 另一方面, 当 ${d_2}/{d_1} < threshold$ 时, 该实例点是离群点, 权重值也应该为0, 从而排除了离群点对特征权重的影响.

3.2 新的特征权重更新公式

本文结合实例权重提出新的类依赖特征权重更新过程如下:

输入: 最大迭代次数T, 以及一个包含N个实例的D维二类数据集: $X = \{ ({x^n},l({x^n}))\} _{n = 1}^N$ , C是数据的类别标签集合, 因为算法用于二类数据集分类, 所以C只包含两个元素.

Step1. 为每个类别的特征权重设置初始权值 ${w_{c,j}} = 0(c \in C,1 \le j \le D)$ .

Step2. 从集合C中取出一个类标签c.

Step3. 从数据集X中随机选取一个类别为c的实例x. 根据如下过程更新权重:

Step3.1. 找出x的k个同类最近邻居集合 $KNN(x,c)$ , 还有k个异类最近邻居集合 $\mathop {KNN}\limits_{l \ne c} (x,l)$ , 以及到 $KNN(x,c)$ 中k个点的距离之和d₁. 到 $\mathop {KNN}\limits_{l \ne c} (x,l)$ 的k个点距离之和d₂.

Step3.2. 将d₁, d₂代入式(5)计算x的实例权重 $IW(x)$ .

Step3.3. c为x的类标签, l为不同于c的类标签, 即集合C中的另一个类. 对两个类别的特征权重 ${w_{c,j}}(j \in D)$ , ${w_{l,j}}(j \in D)$ 进行更新:

$ \begin{array}{l} {\rm{If}}\;\;\;\sum\nolimits_{z \in KNN(x,l),l \ne c} {||x - z|| - \sum\nolimits_{z \in KNN(x,c)} {||x - z|| > 0} } \;:\\ \;\;\;{w_{c,j}} = {w_{c,j}} + IW(x)*(\sum\nolimits_{z \in KNN(x,l),l \ne c} {|{x_j} - {z_j}} | - \sum\nolimits_{z \in KNN(x,c),} {|{x_j} - {z_j}} |)/(T*k)\\ {\rm{else}}:\\ \;\;\;{w_{l,j}} = {w_{l,j}} + IW(x)*(\sum\nolimits_{z \in KNN(x,l),l \ne c} {|{x_j} - {z_j}} | - \sum\nolimits_{z \in KNN(x,c),} {|{x_j} - {z_j}} |)/(T*k) \end{array} $

||x–z||表示点x和点z的欧式距离.

Step4. t=T, 则执行Step5, t<T则返回Step3.

Step5. 若C中所有值都取出, 算法结束, 输出 ${w_c}(c \in C)$ 否则返回Step2.

本文提出的新特征权重更新公式中由于引入了实例权重避免远离类边界的点大幅度影响特征权重值而导致分类边界不能正确分类类边界点. 另一方面从局部权重分类的角度出发修改特征权重更新过程:当异类邻居的特征差值小于与同类邻居的特征差值时减小同类特征权重值, 当异类邻居的特征差值大于与同类邻居的特征差值时增大异类特征权重值.

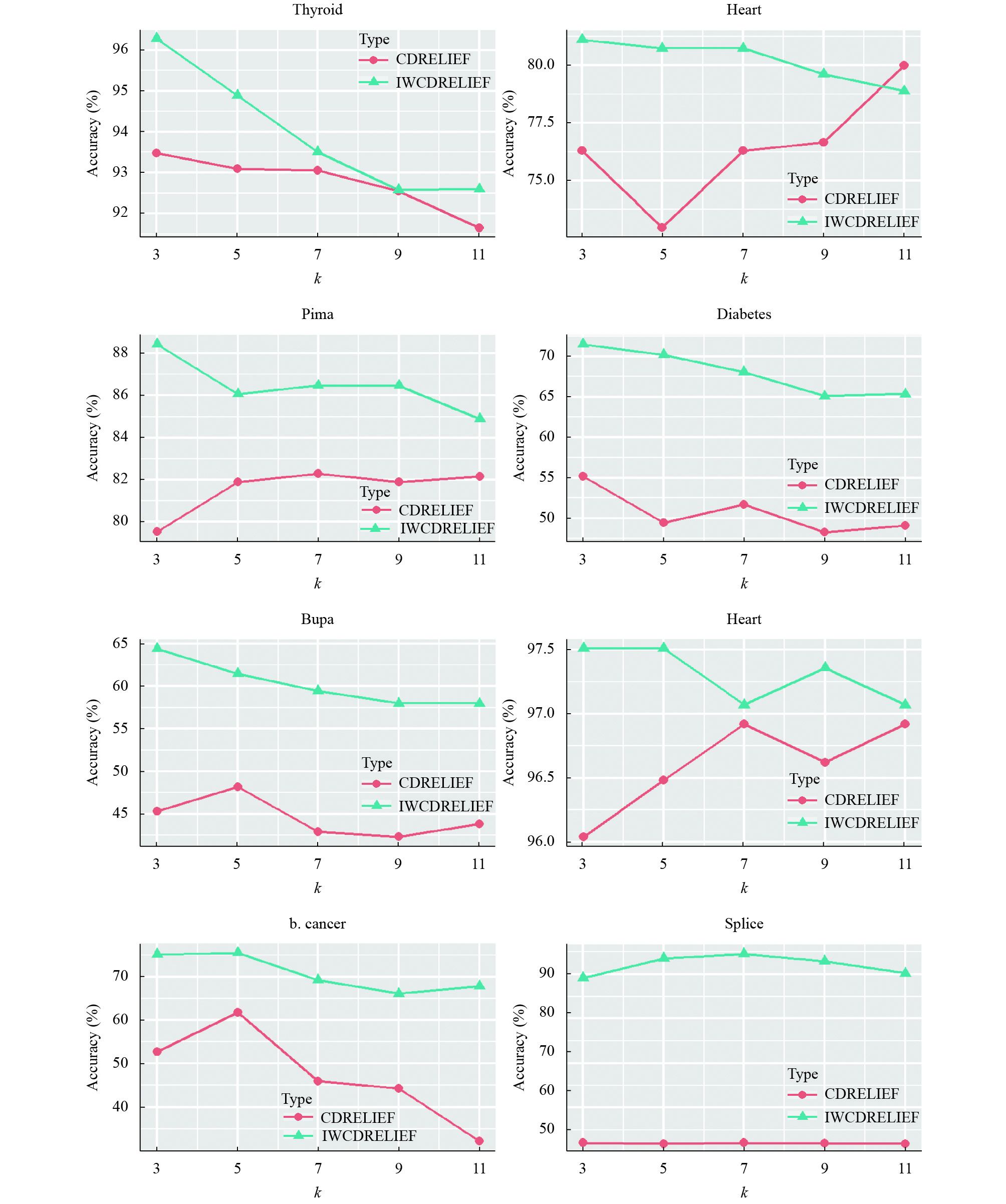
4 实验与分析

实验中采用了8个二类UCI数据集(见表1). 所有数据都用z-score标准化进行预处理. 对每个数据集都进行了10折交叉验证, 取10折交叉准确率的平均值作为最后的准确率. 实验中阈值threshold取值范围从0.1到0.9, 以0.1为间隔一共9个取值, 对每个数据集选择效果最好的那个. 为了验证本文方法的实际效果. 实验中取k=5, 对比了本文提出的算法和类依赖Relief的准确率, 表2显示了两个算法的平均准确度以及标准差. 可以看到本文提出的算法对数据集的分类准确率有很明显的提高, 并且从图一可以看出相比CDRELIEF, 当k取不同值时分类准确率更加稳定且明显高于CDRELIEF.

5 结语

本文通过应用实例权重到类依赖Relief特征权重更新公式中, 提出了具有更好鲁棒性的实例加权类依赖Relief算法, 提出的新算法在8个二类UCI数据集上验证了其有效性. 未来的工作中, 研究如何进一步提出更精确有效的实例加权方案以及如何结合快速学习理论加快算法执行速度, 减小算法时间复杂度是重点方向.