实现机器人自主移动的基础是构建环境地图和定位机器人位置. 在各种研究文献中把机器人环境地图构建和位置定位问题定义成即时定位与地图生成(SLAM)^[1,2], 该问题的复杂性主要在于定位机器人的位置需要获得一个环境特征地图, 而在构建环境特征地图时又估计机器人此刻的位置状态. 地图评估特征估计与机器人位姿估计之间的高度依赖使解决SLAM问题变得十分困难. 早期解决SLAM问题的方法是在卡尔曼滤波器(Kalman Filter, KF)^[3]基础上发展而来, 后来随着粒子滤波(Particle Filters, PF)^[4]理论的提出, Montemerlo^[5]和Paskin^[6]等人提出RBPF算法作为解决SLAM问题的有效方法, 该算法主要根据建立环境地图所需的粒子数量来衡量算法的复杂度, . 因此使用较少的粒子构建较为精确地图是该算法解决的主要问题, 此外重采样步骤可能潜在剔除有效粒子, 从而造成粒子耗散^[7]问题.

在传统的RBPF-SLAM算法实现中需要粒子数量十分巨大, 主要原因在于计算建议分布时只把运动模型数据考虑在内, 造成建议分布与目标分布差距较大, 需要大量的粒子进行拟合. 因此通过把运动模型数据和观测数据两者相结合来优化建议分布, 使之更加接近目标位姿的后验概率分布. 基于优化的建议分布进行粒子采样, 可以显著减少粒子数目. 在传统算法实现中频繁的重采样操作会导致粒子数量枯竭, 通过引入自适应重采样方法来解决该问题, 该方法通过计算当前有效粒子数目来决定是否进行重采样操作, 避免过度的重采样造成粒子数量枯竭现象.

为了随着时间的推移能够高效的更新粒子, 本文引用了二叉树来组织栅格地图^[8]特征, 这种树形结构使得粒子的更新时间复杂度从线性级降低到对数级, 使粒子之间共享相同的地图部分, 从一定程度上节省内存消耗.

1 基于粒子滤波的RBPF算法原理

在RBPF算法中用 $p({x_{1:t}}|{z_{1:t}},{u_{1:t}},{c_{1:t}})$ 表示机器人路径后验分布, 其中X表示机器人位姿, Z表示传感器观测数据, U表示运动数据, C是一致性变量. 用一定数量的粒子来拟合后验分布, 每个粒子表示机器人在真实环境中的一种位姿假设. 采样粒子集 ${Y_t}$ 表示为:

${Y_t} = \{ x_{1:t}^1,x_{1:t}^2,x_{1:t}^3, \cdot \cdot \cdot ,x_{1:t}^m\} $

(1)

其中, 每个粒子 $x_{1:t}^k$ $(1 \leqslant k \leqslant m)$ 都是在t时刻机器人位姿的一个假设状态, k代表粒子集中的第k个粒子, M是代表粒子总数. 每个粒子 $x_{1:t}^k$ 形式表示为:

$ x_{1:t}^k = \{ {(x,y,\theta )^T},(\mu _1^k,\Sigma _1^k),(\mu _2^k,\Sigma _2^k), \cdot \cdot \cdot ,(\mu _N^k,\Sigma _N^k)\} $

(2)

每个粒子包含一个机器人的位姿估计 ${(x,y,\theta )^T}$ , 而且包含一个具有均值 $\mu _j^k$ 和协方差 $\Sigma _j^k$ 的卡尔曼滤波集合, 这个集合表示每个粒子对于地图中出现特征的估计和机器人位姿的状态, 用 $\mu _j^k$ 和 $\Sigma _j^k$ 表示出现在地图中的每个特征位置估计的均值和方差.

RBPF粒子滤波器可以表示为如下因式分解:

$\begin{gathered} p({x_{1:t}},m|{z_{1:t}},{u_{1:t - 1}}) = \\ p(m|{x_{1:t}},{z_{1:t}}) \bullet p({x_{1:t}}|{z_{1:t}},{u_{1:t - 1}}) \\ \end{gathered} $

(3)

该公式用两个独立的后验概率乘积表示SLAM问题: $p({x_{1:t}}|{z_{1:t}},{u_{1:t - 1}})$ 表示机器人路径轨迹的后验概率, $p(m|{x_{1:t}}, $ ${z_{1:t}})$ 表示机器人的环境地图后验概率. 这种概率分解在解决SLAM问题时可以先计算机器人的位姿轨迹, 然后在已知机器人位姿情况下的计算更新当前环境地图.

算法步骤描述如下:

1)采样: 根据建议分布从t–1时刻粒子集合 $\scriptstyle {Y_{t - 1}}$ 采样获取t时刻粒子的先验分布集合 $\scriptstyle Y_t^ - $ , 建议分布使用运动模型 $\scriptstyle p({x_t}|{x_{t - 1}},{u_t})$ .

2)计算权重: 计算每个粒子的权重, 权重w反映了建议分布与目标后验分布的差距.

3)重采样: 根据每个粒子的权重进行重采样, 从临时粒子集合 $\scriptstyle Y_t^ - $ 中抽取更换M个粒子, 结果产生的M个粒子形成新的最终粒子集 $\scriptstyle {Y_t}$ .

4)更新地图: 对于每个粒子根据传感器观测数据 $\scriptstyle {z_{1:t}}$ 和机器人当前位姿 $\scriptstyle {x_t}$ 更新地图中的每个特征 $\scriptstyle m_t^i$ .

$\qquad\qquad\;\;\;\;\;\;\;\;\qquad\scriptstyle {m^i} \sim p({m^i}|{x_t},{z_{1:t}})\quad\quad\qquad\;\;\;\;\;\qquad\qquad(4)$

2 RBPF-SLAM的改进算法

在传统的RBPF算法实现中, 在进行粒子采样时, 粒子滤波器使用机器人的远动模型计算建议分布, 使用传感器观测模型计算采样粒子的权重, 权重更新公式为:

$w_t^i \propto p({z_t}|x_t^i,m_{t - 1}^i) \cdot w_{t - 1}^i$

(5)

如果距离传感器的精度比里程计的精度高, 采用上述的建议分布会导致粒子之间的权重差距比较大, 具有较高权重的粒子分布在观测后验高概率区域. 而且在传统的算法实现中每一步都要进行重采样操作, 频繁的重采样会潜在的提出有效粒子导致粒子耗散, 以及降低算法的计算效率, 影响实时性.

2.1 改进建议分布

解决传统算法的建议分布的不足, 一种普遍的解决方法, 尤其是在定位方面, 是使用一个平滑的似然函数, 避免粒子在观测似然函数分布之外的区域权值较低. 但是这种方法会丢弃一部分距离传感器采集到的信息, 会导致建立的地图不准确. 解决该问题的一种改进方案, 在采集下一代粒子时把最近的观测数据 ${z_t}$ 考虑进来. 通过把观测数据 ${z_t}$ 结合到建议分布中, 从而在采样时, 只采集分布在观测概率函数区域内的粒子. 此改进的建议分布如下:

$\begin{gathered} p({x_t}|m_{t - 1}^i,x_{t - 1}^i,{z_t},{u_{t - 1}}) = \frac{{p({z_t}|m_{t - 1}^i,{x_t}) \cdot p({x_t}|x_{t - 1}^i,{u_{t - 1}})}}{{p({z_t}|m_{t - 1}^i,x_{t - 1}^i,{u_{t - 1}})}} \\ \end{gathered} $

(6)

使用该建议分布在计算权重时, 公式为:

$w_t^i \propto w_{t - 1}^i \cdot p({z_t}|m_{t - 1}^i,x_{t - 1}^i,{u_{t - 1}})$

(7)

在实际的实现中无法通过公式(6)直接采样下一代临时粒子样本集. 解决办法是在建议分布的峰值附近区域内的求取一个近似的正态分布函数, 并用该函数进行采样.

首先, 使用t–1时刻的粒子位姿 $x_{t - 1}^i$ , 计算期望粒子位姿 $x_t^{i - }$ :

$x_t^{i - } = g(x_{t - 1}^i,{u_t})$

(8)

然后, 根据距离传感器采集到的数据计算具有最大观测概率的机器人目标位姿 $\overset{\sim }{\mathop{x}}_{t}^{i}$

$\overset{\sim }{\mathop{x}}_{t}^{i} = \arg {\max _x}p(x|m_{t - 1}^i,{z_t},x_t^{i - })$

(9)

然后在目标位姿附近选取K个样本点, 依据以下公式进行采样:

$ {x_k}\sim\{ {x_j}|\;\;\; |{x_j} - \overset{\sim }{\mathop{x}}_{t}^{i}|\;\;\; < \;\;\; \Delta \} $

(10)

然后使用采集的K个样本点 $\{ {x_1},{x_2}, \cdots ,{x_k}\} $ , 使用蒙特卡洛计算正态分布函数的参数 ${ N}(\mu _t^i,\Sigma _t^i)$ .

另 $ {x_j} \in \{ {x_1},{x_2}, \cdots ,{x_k}\} $ , 则

$\eta _t^i = \sum\limits_{j = 1}^k {p({z_t}} |m_{t - 1}^i,{x_j}) \cdot p({x_j}|x_{t - 1}^i,{u_{t - 1}})$

(11)

$\mu _t^i = \frac{1}{{\eta _t^i}}\sum\limits_{j = 1}^k {{x_j}} \cdot p({z_t}|m_{t - 1}^i,{x_j}) \cdot p({x_j}|x_{t - 1}^i,{u_{t - 1}})$

(12)

$\begin{gathered} \Sigma _t^i = \frac{1}{{\eta _t^i}}\sum\limits_{j = 1}^k {({x_j}} - u_t^i) \cdot {({x_j} - u_t^i)^T} \cdot \\ p({z_t}|m_{t - 1}^i,{x_j}) \cdot p({x_j}|x_{t - 1}^i,{u_{t - 1}}) \\ \end{gathered} $

(13)

通过此方法, 我们可以获得此改进建议分布的近似公式, 在此公式中融合了机器人的里程计数据 ${u_{t - 1}}$ 和最新的观测数据 ${z_t}$ , 可以更加有效准确获取采样粒子.

2.2 自适应重采样

在重采样时, 权值 ${w^i}$ 小于阈值的粒子会被从高权值区域附近采样的粒子所替代. 一方面重采样是必须的, 因为只需要有限的粒子来近似目标分布; 另一方面重采样可能剔除有效粒子导致粒子数量枯竭. 在本文中根据当前的有效粒子数目来决定是否要执行从采样操作. 有效粒子数目 ${N_{eff}}$ 表示粒子集的退化程度, 值越小退化越严重, 需要进行重采样. ${N_{eff}}$ 如下定义:

${N_{eff}} = \frac{1}{{\sum\nolimits_{i = 1}^M {{{\mathop {(w}\limits^ \sim }^i}{)^2}} }}$

(14)

其中, M为粒子数目, ${{\overset{\sim }{\mathop{w}}}^{i}}$ 是粒子 ${x_i}$ 的归一化化权重. ${N_{eff}}$ 越大说明粒子集的多样性越好, 不需要重采样, 只有 ${N_{eff}}$ < N/2时才需要重采样.

2.3 改进算法流程描述

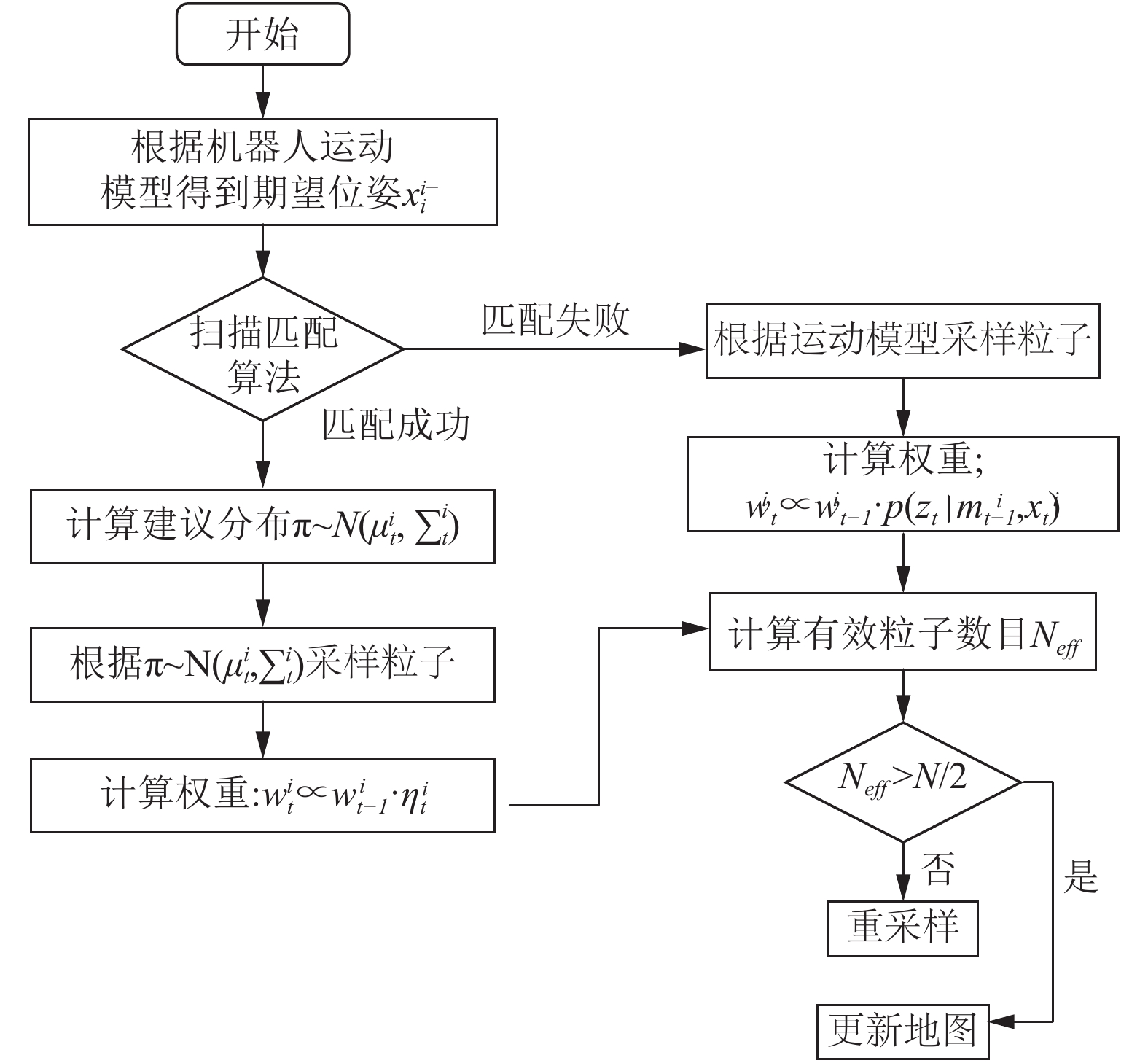
1)使用机器人运动模型计算粒子的期望位姿 $x_t^{i - }$ .

2)根据扫描匹配算法估计具有最大观测后验概率的机器人目标位姿 $\overset{\sim }{\mathop{x}}\,_{t}^{i}$ .

3)计算建议分布: 根据公式(11)~(13)计算建议分布 $\pi \sim N(\mu _t^i,\Sigma _t^i)$ .

4)采样: 根据所求的建议分布进行粒子采样.

5)计算权重: 根据公式 $w_t^i \propto w_{t - 1}^i \cdot \eta _t^i$ 计算粒子权重.

6)依据公式(14)计算当前粒子集的有效数目, 当 ${N_{eff}}$ <N/2时需要重采样.

7)根据传感器观测数据更新地图.

算法流程图见图1.

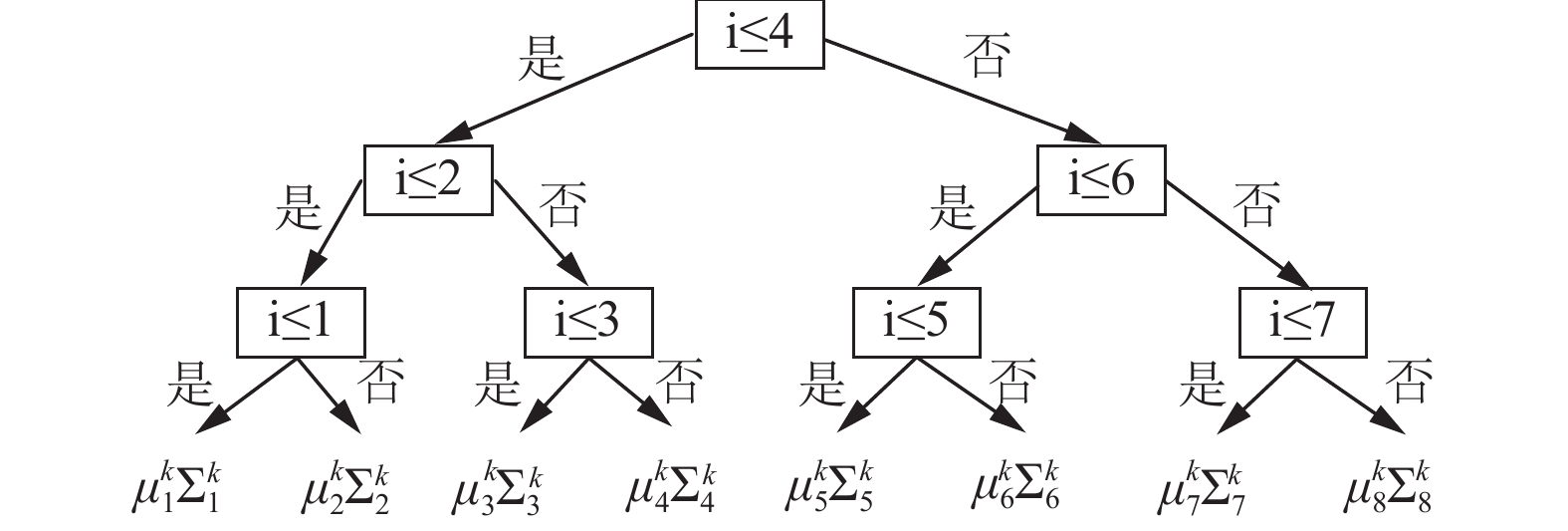
3 算法的高效实现

在RBPF-SLAM算法的实现中每一步地图更新好像均需要时间O(MN), 其中, M表示粒子数目, N表示地图中的特征数量. 每次更新必须处理M个粒子, M的线性复杂度是必须的. N的线性复杂度是重采样的结果, 当粒子在重采样步骤中不止一次被抽中时, 在一般的实现中会复制属于该粒子的整个地图. 通过引入更多选择性更新的数据结构来表示粒子, 可以避免线性复制的开销. 其基本思想是将地图组织为平衡二叉树, 如图2所示.

假设在t时刻合并了一个新的控制 ${u_t}$ 和新的测量 ${z_t}$ , ${Y_t}$ 里的每个新粒子与 ${Y_{t - 1}}$ 里对应的粒子主要存在两点不同: 第一, 得到不同的位姿估计; 第二, 观察到的特征的高斯参数 $\mu _i^k$ 和 $\Sigma _i^k$ 会被更新, 所有的其它特征的参数不变. 因此, 在复制粒子时, 在代表所有特征的树里, 只有一个路径被修改, 所以可以在对数时间内完成更新. 对于树节点的内存释放, 是通过给每个节点分配一个指针计数器. 新创建的节点计数器初始化为1, 当其它粒子创建指针指向该节点时, 计数器增加, 指针移除时计数器减少, 当计数器为零时释放该节点. 实验表明使用树形结构组织地图可以大量节省内存, 加快地图更新速度.

4 实验结果

实验的硬件平台配置包括TurtleBot机器人、里程计和激光雷达, TurtleBot机器人是一款基于ROS操作系统的机器人配备用里程计和二维激光雷达. 软件平台配置采用ROS的kinetic版本, 运行平台为Ubuntu操作系统, 并采用Python作为脚本编程语言. ROS自带3维可视化工具RVIZ(如图3所示) , 可进行人机交互.

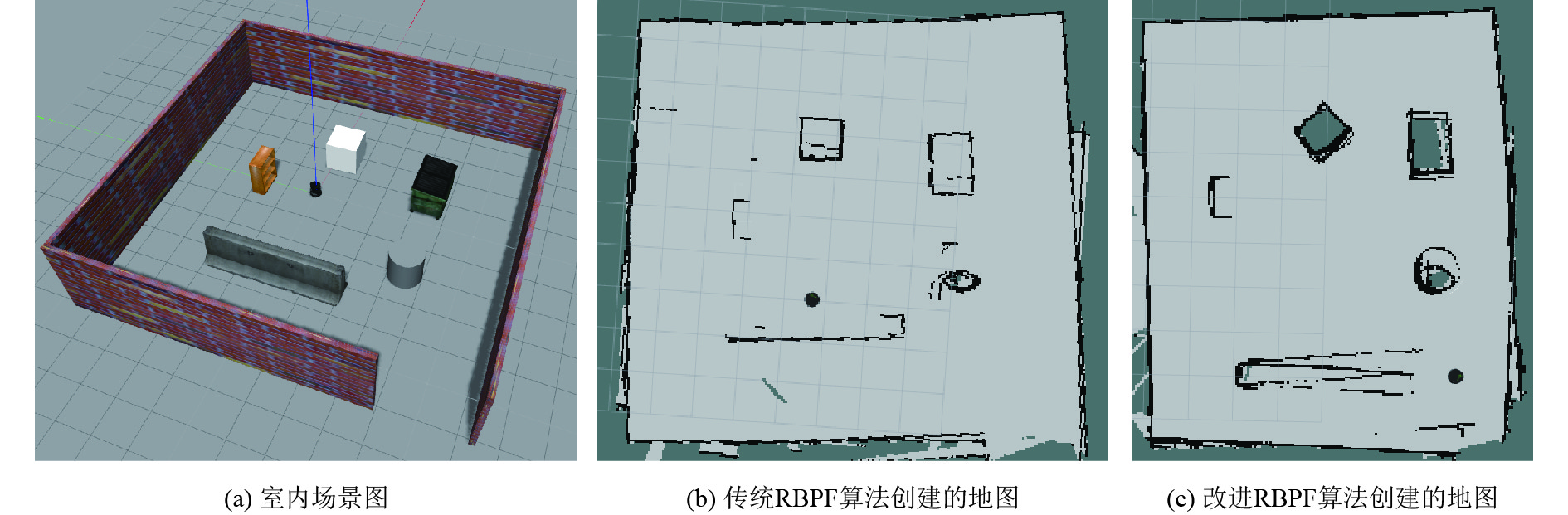
在图4中分别展示了由传统RBPF-SLAM算法和改进算法创建的室内地图. 在图中深灰色表示未探测区域, 浅灰色表示已扫描区域, 其中被包围的深灰色区域表示扫描到的地图特征(障碍物). 本实验的地图大小为10米 $ \times $ 10米. 图4(a)是用传统算法创建的二维栅格地图, 采用了20个采样粒子; 图4(c)是由改进算法创建的地图, 只采用了10个采样粒子, 从效果来看创建的地图更加清晰精确.

从图4的对比实验效果来看, 相比于传统的RBPF-SLAM算法, 改进的算法使用更少的粒子数目, 更少的计算资源以及更少的存储资源可以创建出精确度更高, 效果更好的环境地图. 在改进算法中结合传感器观测数据优化建议分布, 使得建议分布更加接近于机器人真实位姿的目标分布. 粒子数量是衡量RBPF算法性能的主要指标, 因此改进的算法可以显著降低粒子数目, 节省计算资源.

而且在改进算法的实现时采用了树形数据结构来表示粒子, 这样可以大量节省内存的消耗. 在图5中给出传统RBPF算法与该进算法消耗内存的对比. 纵坐标表示粒子数, 横坐标表示内存消耗. 通过引用树形结构可以有效减小内存使用情况.

分析比较改进算法的运行时间, 在表1和表2中记录了在不同的粒子数目下, 改进算法和传统算法主要步骤执行时间. 能够看到, 建立环境地图所需时间和粒子数量近似成正比关系. 改进算法所需的计算时间明显少于传统算法所需的计算时间, 这是由于改进算法的采样准确度高, 从而大大减少了所需的粒子数目, 而且在算法实现时通过引入树形结构减少了粒子的查找与更新时间, 大大提高了算法的计算效率.

5 总结

在本文中通过对传统RBPF-SLAM算法优化改进, 在计算时把运动模型与观测信息相结合优化建议分布, 可以显著减少采样的粒子数量; 引入自适应的重采样策略, 避免不必要的从采样操作, 避免粒子耗散, 根据 ${N_{eff}}$ 适时的采样随机粒子维持粒子集的多样性. 通过引入更多选择性更新的数据结构来表示粒子, 可以避免线性复制的开销. 其基本思想是将地图组织为平衡二叉树, 减少了粒子的查找与更新时间, 提高了算法性能. 从实验结果来看对算法的优化改进从计算效率, 地图精度以及存储消耗等方面都要优于传统算法.