膜计算(membrane computing)是自然计算中最年轻的一个分支, 是从细胞的结构、器官和组织等细胞群的信息处理协作方式中抽象出的一种计算模型. 膜计算自提出以来, 受到了众多学者的广泛关注[1]. 研究表明: 理论上膜计算模型具有与图灵机同等的计算能力, 甚至有可能突破图灵机的局限性[2–4]. 目前, 膜计算的研究主要在理论、应用和实现三个方面[5]. 在膜计算应用方面, 它已经成功地应用在优化领域[6], 故障诊断[7], 移动机器人控制[8], 计算机图形学与语言学[9]等领域.
移动机器人膜控制器(membrane controller)是利用膜系统设计的一种移动机器人认知、行为控制器, 是膜计算在机器人控制方面的一种典型应用. 利用膜系统设计机器人控制器主要优势在其天然的并行性和分布式. 膜系统各层膜上的运算可以分布在机器人不同的微处理器上, 各层膜的计算是并行的[10]. 因此, 在设计过程中, 不需要额外考虑控制器并行性、分布性的实现, 可以专注于膜控制器功能的实现. 膜控制器最早由罗马尼亚布加勒斯特大学自然计算团队的Buiu提出[11]. 2011年, Buiu等人首次将数值膜系统(Numerical P Systems, NPS)应用于机器人控制, 并在Epuck机器人和Khepera3机器人上设计实现了机器人的避障行为、随墙行为以及跟随行为膜控制器, 证明了膜控制器的可行性[8]. 随后, Cristian等人将膜控制器应用于Koala机器人, 进一步验证了其可行性[12]. 由于数值膜系统膜内规则数的限制, 导致了需要大量的膜来存放规则. 为了提高膜控制器设计效率, Pavel和Buiu在此基础上提出了酶数值膜系统(Enzymatic Numerical P Systems, ENPS), 并将酶数值膜系统应用于控制移动机器人的避障行为[13].
目前, 绝大多数基于膜系统进行避障的机器人其膜控制器参数固定, 使移动机器人无法同时兼顾避障效果和无障碍物时的巡航速度. 针对该问题, 本文提出了一种基于酶数值膜系统的移动机器人避障控制方法. 该方法采用酶数值膜系统结构, 利用膜之间的信息交流, 实现多个膜融合多个传感器的距离信息, 根据融合的距离信息调节巡航速度, 从而兼顾移动机器人的避障效果和行走速度, 实现了更优的避障控制.
1 避障行为控制律分析避障控制律是膜控制器的设计基础, 移动机器人避障行为的依据. 目前, 避障行为膜控制器主要基于式(1)(2)的控制律设计[8,12,13]. 该控制律通过传感器获得的机器人与障碍物之间的距离信息, 计算避障所需的左右轮速度, 用于控制机器人两轮速度, 实现机器人差速避障.
| $ l{\rm{e}}ftSpeed = CruiseSpeed + \sum {{s_i}*weightLef{t_i}} $ | (1) |
| $ rightSpeed = CruiseSpeed + \sum {{s_i}*weightRigh{t_i}} $ | (2) |
其中, leftSpeed和rightSpeed分别为左右轮的速度; CruiseSpeed为巡航速度; si为第i个传感器的值, 障碍物距离移动机器人越近, 该值需越大, 未检测到障碍物时, 该值为0; weightLefti和weightRighti分别为第i个传感器对应左右轮速度的权重.
控制律中巡航速度CruiseSpeed为定值, 取值为(0, Vmax), Vmax为移动机器人最大行走速度. 传感器权值weightLefti和weightRighti用于表示不同位置的传感器对左右轮速度的影响, 取值规律一般为:
位于机器人左前侧的传感器对应的weightLefti为正, weightRighti为负;
位于机器人右前侧的传感器对应的weightLefti为负, weightRighti为正;
位于机器人后侧的传感器对应的weightLefti、weightRighti为0;
左右侧传感器对应的权值weightLefti(weightRighti)互为相反数;
传感器位置越靠近机器人正前方, 对应权值的绝对值越大.
该种取值方式使得移动机器人探测到左侧障碍物时, 左轮速度增加, 右轮速度减少, 向右避开障碍物; 右侧障碍物同理. 且障碍物越靠近机器人正前方, 左右轮速度差越大. 本文之后的讨论均在该取值规律下进行.
从移动机器人运动学分析, 两轮差速驱动移动机器人的运动学方程为[14]:
| $v = \frac{{{v_r} + {v_l}}}{2}$ | (3) |
| $w = \frac{{{v_r} - {v_l}}}{l}$ | (4) |
其中, v为机器人质心处的线速度, 即机器人前进速度; w为机器人的转向角速度, 即机器人旋转角速度; vl和vr分别为机器人的左右轮线速度; l为机器人两驱动轮的轮距.
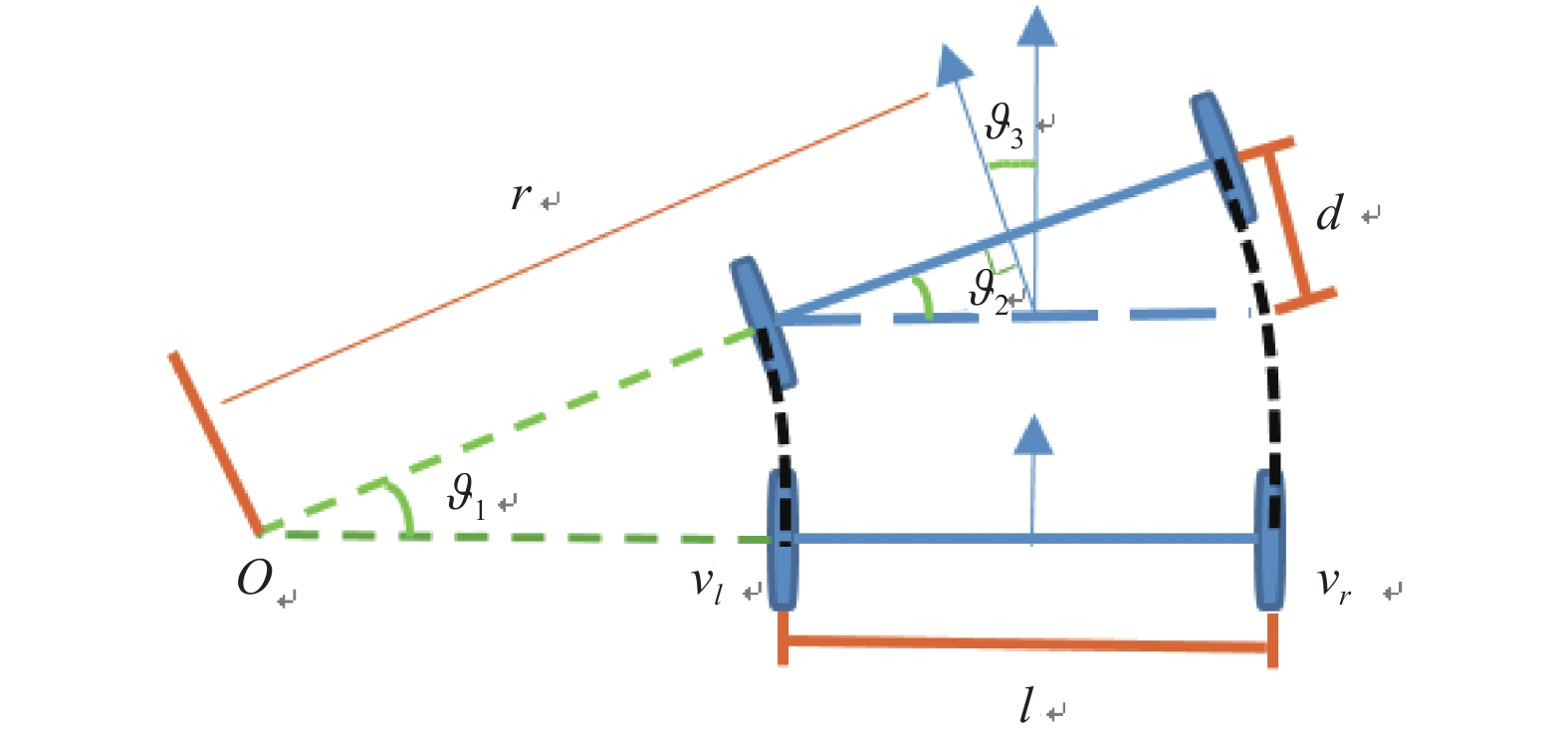
由文献[15]可知: 移动机器人左右轮速度恒定, 但取值不同时, 机器人运动轨迹为圆形. 轨迹半径为r, 如图1所示.
|
图 1 双轮差速机器人运动学模型 |
| $r = \frac{v}{w}$ | (5) |
其中, r为移动机器人圆周运动半径.
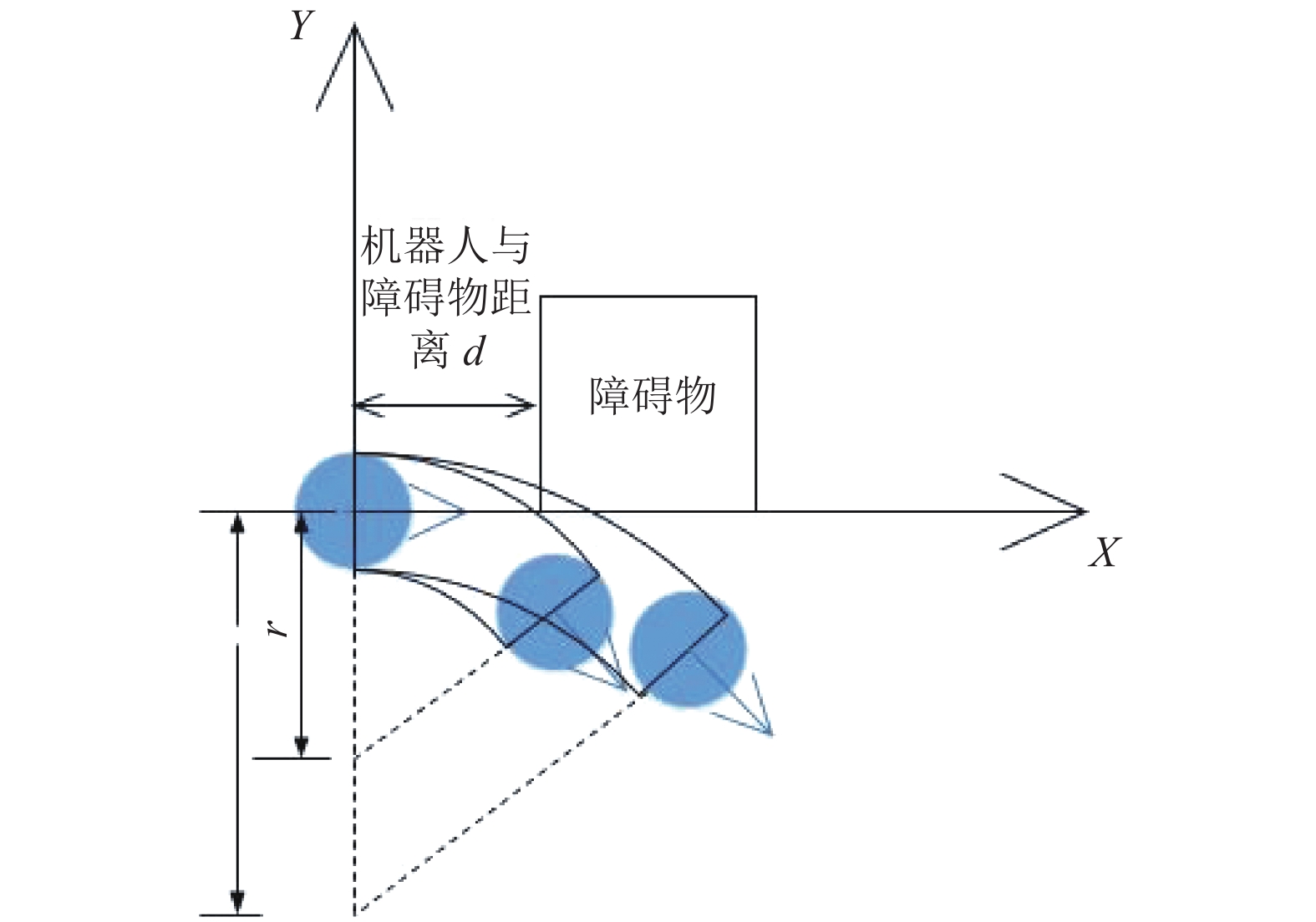
移动机器人行走过程中, 障碍物环境十分常见, 在如图2所示的障碍物场景中, 分析移动机器人前进速度v, 旋转角速度w对机器人避障距离d的影响.
|
图 2 移动机器人避障距离分析 |
假设移动机器人避障过程中前进速度v, 旋转角速度w恒定. 机器人恰好避开相距d的障碍物, 机器人轨迹运动半径为r.
当旋转角速度w一定时, 前进速度v增大, 由式(5)可知: 机器人轨迹运动半径r增大, 避障距离d增大, 如图2所示.
当前进速度v一定时, 旋转角速度w增大, 由式(5)可知: 机器人轨迹运动半径r减小, 避障距离d减小.
分析控制律中巡航速度对避障距离的影响. 将式(1)、式(2)代入式(3)、式(4)得:
| $v = CruiseS\!\!peed + \frac{1}{2}\sum {{s_i}*(weightLef{t_i} + weightRigh{t_i})} $ |
| $w = \frac{{\sum {{s_i}*(weightRigh{t_i} - weightLef{t_i})} }}{l}$ |
按照权值取值规律, weightLefti、weightRighti为相反数. 上述公式简化为:
| $v = CruiseSpeed$ | (6) |
| $w = \frac{{\sum {{s_i}*(weightRigh{t_i} - weightLef{t_i})} }}{l}$ | (7) |
由式(6)和式(7)可知, 巡航速度CruiseSpeed等于机器人前进速度v. 结合前述分析可得: 避障距离与控制律中巡航速度成正相关.
由于控制律中巡航速度为固定值, 移动机器人初始巡航速度大, 机器人避障效果差, 初始巡航速度小, 行走速度慢. 机器人无法兼顾避障效果和无障碍物时的行走速度.
2 自适应巡航速度的酶数值膜控制器移动机器人避障过程中, 控制器计算速度对避障效果有着很大的影响. 膜系统具有分布式、并行性的特点, 有助于提高控制器的计算速度, 适合机器人控制器的设计. 酶数值膜系统能够处理数值变量、每个膜内可以允许存在多条规则, 广泛应用于移动机器人膜控制器设计中.
2.1 避障控制律的改进由第1节分析可知: 传统膜控制方法存在移动机器人前进速度和避障效果之间的矛盾. 为了兼顾移动机器人无障碍物时的前进速度和有障碍物时的避障效果, 本文对传统避障控制律进行改进, 如式(8), 使巡航速度随障碍物与机器人间的距离自适应变化. 当障碍物距离移动机器人近时(si大), 巡航速度减小; 当障碍物距离移动机器人大或无障碍物时(si小), 巡航速度大.
| $ CruiseS\!\!peed = {C_0}*{a^{\sum {{s_i}*{w_i}} }} $ | (8) |
其中, CruiseSpeed为巡航速度; C0为设定速度, 无障碍物时, C0=CruiseSpeed; si为第i个传感器的值, 机器人与障碍物距离越近, si越大; wi为第i个传感器值的权重; a为底数(0<a<1),a值小, CruiseSpeed下降幅度大.
式(8)中,
(1) x=0时, y=1;
(2) 函数单调递减, 且当x大于0时, y在(0, 1)间取值.
因此, 障碍物距离衡量值越大, 即障碍物离机器人越近时, CruiseSpeed越小且CruiseSpeed不会因为距离衡量值过大, 出现负值(机器人向后运动). 衡量值为0(无障碍物或已避开障碍物)时, CruiseSpeed=C0, 机器人以设定速度前进.
2.2 酶数值膜控制器的设计依据避障控制律, 即式(1)、式(2)、式(8), 本文设计了酶数值膜控制器, 如图3所示. 膜控制器的输入变量为传感器值si, 权重weightLefti和weightRighti, 底数a, 设定速度C0; 输出变量为左右轮速度leftSpeed、rightSpeed. 控制律的计算可分为权值乘累加(即

|
图 3 移动机器人避障行为的酶数值膜控制器 |
(1)第一次循环执行步骤如下:
Sensori膜中的3条规则和CruiseSpeed膜中的规则1激活(值产生规则中存在变量的值小于酶变量);
Sensori膜中规则1、2、3将传感器值和权值累加给变量SWL、SWR、SW(权值乘累加部分, 其中变量SWL为左轮权值乘累加值, SWR为右轮权值乘累加值, SW为障碍物距离衡量值);
CruiseSpeed膜中规则1将变量f赋值1, e赋值2. 确保变量f始终为1以及酶变量e在第二次循环中起作用(激活规则). 值产生规则中的0*e用于防止酶变量e的值不断累积.
(2)第二次循环执行步骤如下:
CruiseSpeed膜中的规则2-5激活(值产生规则中存在变量的值小于酶变量);
CruiseSpeed膜中规则2将酶变量e0赋值2. 确保酶变量e0在第三次循环中起作用. 值产生规则中的0*e0用于防止酶变量e0的值不断累积;
CruiseSpeed膜中规则3将设定速度C0和指数相乘赋给变量Cruise_Speed(自适应巡航速度计算);
CruiseSpeed膜中规则4、5分别将变量SWL、SWR值赋给变量SWL_temp、SWR_temp. 用于保存SWL、SWR的值.
(3)第三次循环执行步骤如下:
Avoid膜中的规则1、2激活(值产生规则中存在变量的值小于酶变量);
Avoid膜中规则1、2分别将巡航速度Cruise_Speed和SWL_temp、SWR_temp相加赋给变量leftSpeed、rightSpeed(左右轮速度计算). 完成控制律的计算.
3 实验结果与分析为了验证酶数值膜控制器的避障控制效果, 本文分别在Pioneer3-DX机器人仿真平台和实物上进行测试. Pioneer3-DX具有16个环形分布传感器, 如图4所示, 故酶数值膜控制器中存在16个 Sensori膜(i取1–16).

|
图 4 移动机器人声呐传感器分布图 |
设计如图5所示的固定巡航速度酶数值膜控制器作为对比实验. 在以下实验中, 膜控制器1表示固定巡航速度的酶数值膜控制器, 膜控制器2表示本文自适应巡航速度的酶数值膜控制器.

|
图 5 固定巡航速度酶数值膜控制器 |
表1为两种膜控制器的默认参数取值(特殊说明除外). 其中, 膜控制器1巡航速度及膜控制器2设定速度取为500 mm/s, 使无障碍时移动机器人能够较快移动. 权重weightLeft (Right), wi根据前述取值规律及移动机器人巡航速度确定. 底数a根据速度下降需求取定, a越小, 巡航速度下降越快. 表中横杠表示相应控制器中不存在该变量.
为了方便实验, 设置机器人传感器的检测范围为1000 mm. 在检测范围内, 对Pioneer机器人声呐传感器所获距离数据xi进行线性变换, 使其满足控制律要求.
| ${s_i} = - {x_i} + 1000$ |
其中, xi为第i个声呐传感器检测的机器人与障碍物的距离(单位: mm), si为线性变换后的传感器值, xi的变化从0到1000 mm, 线性变换后, si从1000到0. 处理后的声呐传感器值si作为2种酶数值膜控制器的输入.
| 表 1 两种膜控制器的参数值 |
3.1 仿真实验
为了验证本文设计的酶数值膜控制器的有效性, 在机器人仿真平台上进行最小避障距离实验以及复杂环境实验. 仿真实验所用的计算机为联想G470 2.3 GHz, 6 G RAM, 操作系统为Window7, 仿真平台为MobileSim, 仿真机器人为Pioneer3-DX, 机器人尺寸52×40 cm.
(1) 最小避障距离实验
为了验证第1节得出的传统膜控制器巡航速度CruiseSpeed对移动机器人最小避障距离的影响规律, 进行最小避障距离实验. 通过改变膜控制器1中巡航速度CruiseSpeed, 测量移动机器人最小避障距离. 本文使用的避障测量场景如图6, 障碍物尺寸为40×40 cm. 移动机器人初始速度达到巡航速度, 测量移动机器人避开障碍物所需的最小距离. 注: 本文测量间隔为5 cm, 该距离相对移动机器人尺寸已足够小.
实验结果如表2: 随着CruiseSpeed的增大, 移动机器人避障所需的最小距离越大, 避障效果越差.
在该测量场景下, 膜控制器2的最小避障距离为50 cm, 相当于巡航速度CruiseSpeed为320 mm/s的膜控制器1的避障距离, 而其无障碍物时的速度为500 mm/s, 兼顾了避障效果和无障碍物行走速度, 控制效果更佳.

|
图 6 避障距离测量场景 |
| 表 2 不同巡航速度所需的最小避障距离 |
(2) 复杂环境实验
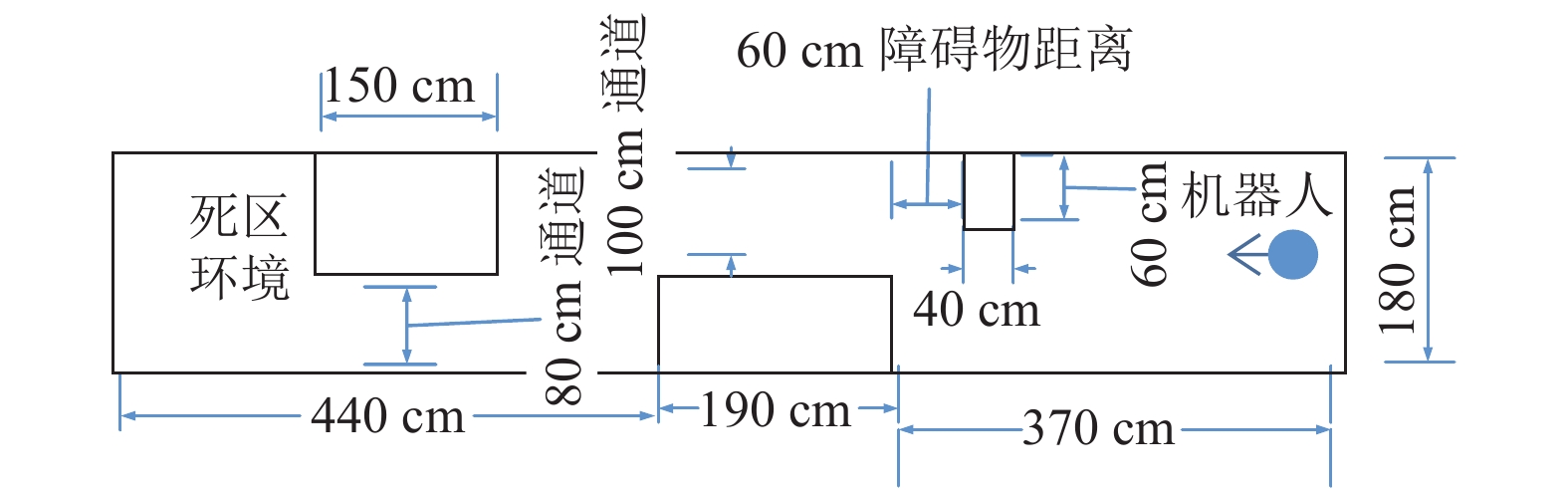
为了验证本文设计的自适应膜控制器在复杂环境的有效性, 设计如图7所示的复杂环境进行实验. 环境中包括死区、100 cm通道、80 cm通道、间隔60 cm的两障碍物. 将移动机器人置于此环境中, 分别在膜控制器1和膜控制器2的控制下进行行走. 比较膜控制器的避障效果, 并采集行走过程中移动机器人左右轮速度、前进速度、旋转角速度、巡航速度及障碍物距离衡量值, 进行比较分析.
|
图 7 复杂环境场景 |
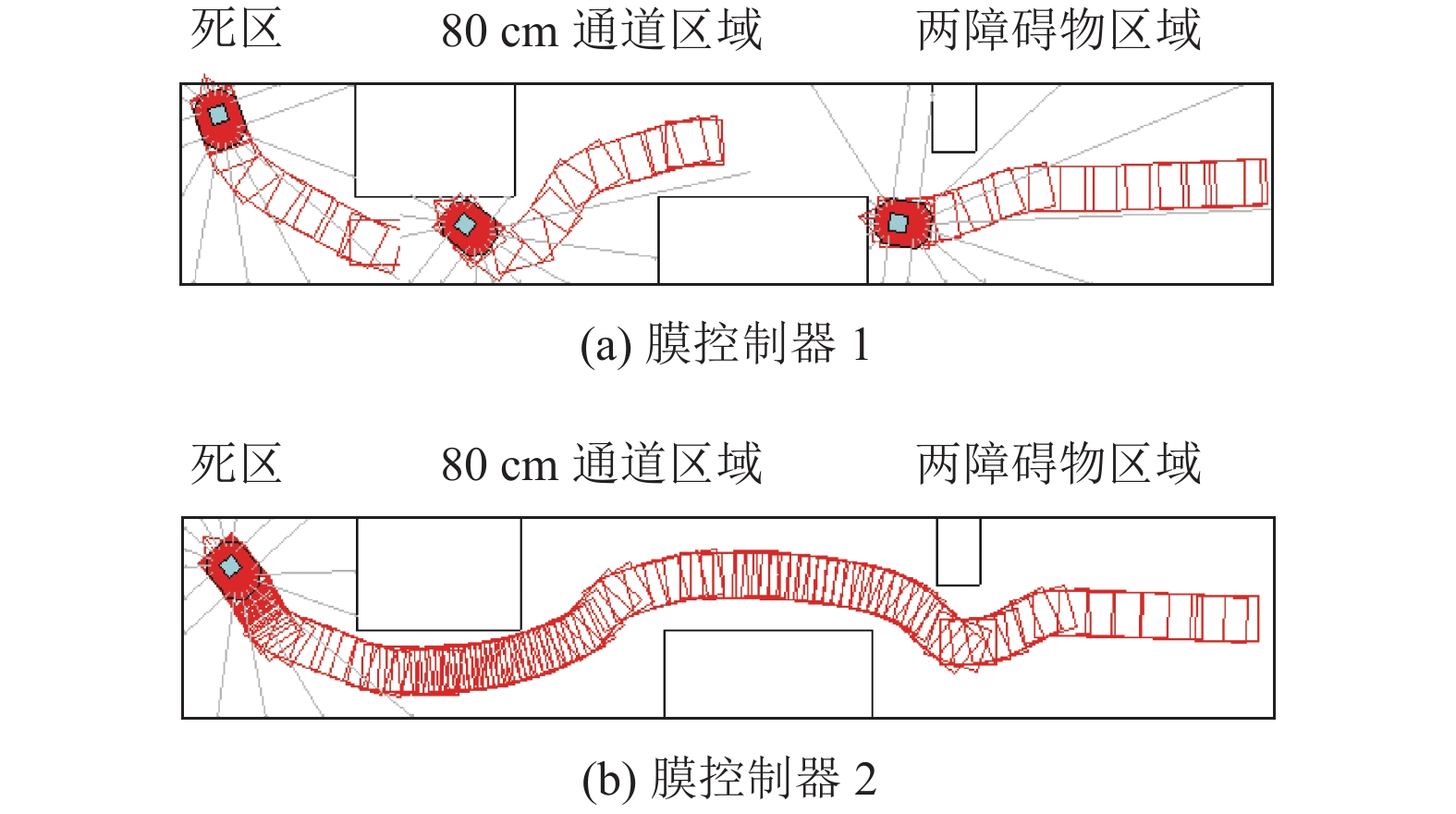
实验结果如图8所示, 图8(a)为膜控制器1控制下的移动机器人仿真结果: 机器人在2个相隔60 cm的障碍物处发生碰撞; 将其手动放置到100 cm通道中, 继续实验, 其在80 cm通道处发生碰撞; 将其放置到死区环境中, 其与死区环境相撞. 图8(b)为膜控制器2的仿真结果: 机器人顺利避开障碍物, 通过通道, 最终在死区环境中停下. 通过实验结果可以看出固定巡航速度的膜控制器机器人容易因反应时间短、角度调整不及时, 发生碰撞; 而自适应巡航速度机器人可随着障碍物的距离而改变速度, 进而有效避开障碍物.
对比图9、10的速度值, 可以进一步看出: 避障过程中, 由于膜控制器1的巡航速度、前进速度不变, 为500 mm/s, 在两障碍物区域和80 cm通道区域, 机器人反应时间短, 约为36、30个执行次数(膜控制器1平均每个执行次数耗时0.157 s), 发生碰撞; 死区环境由于左右侧传感器同时检测到障碍物且传感器值相近, 造成控制律中权值乘累加部分小, 旋转角速度小, 导致碰撞. 而膜控制器2巡航速度随着障碍物的接近而减小, 在障碍物区域速度降至150 mm/s, 80 cm通道区域降到100 mm/s, 机器人前进速度变化情况与巡航速度相同, 从而使移动机器人有更长的避障反应时间, 分别约为70、180个执行次数(膜控制器2的平均每个执行次数耗时0.122 s); 在死区环境下速度降为0, 避免发生碰撞.
|
图 8 复杂环境实验结果 |

|
图 9 膜控制器1控制下的移动机器人速度 |
3.2 实物实验
由于仿真实验条件理想, 不存在声呐传感器探测不到障碍物、机器人打滑等情况. 为了验证膜控制器在实物中的控制效果, 分别使用膜控制器1和膜控制器2在如图11场景中进行实验. 场景中包括间隔50 cm的3个障碍物, 110 cm的通道、80 cm通道以及死区环境. 实物机器人使用Adept MobileRobots公司制造的Pioneer3-DX双轮移动机器人, 该机器人摆动半径为26 cm, 重9 kg, 16个环形分布声呐传感器, 2个高扭矩马达, 配有Window7系统、i5处理器的工控机.

|
图 10 膜控制器2控制下的移动机器人速度 |

|
图 11 实物场景 |
膜控制器1控制下的实验结果如图12所示: 图12(a)–12(h)为移动机器人在多障碍物区域的实验结果, 图12(i)–12(l)为通道区域的实验结果, 图12(m)– 12(p)为死区的实验结果. 膜控制器1作用下的移动机器人在相隔50 cm的多障碍物区域、通道区域、死区均发生碰撞.
从移动机器人速度图13进一步看出: 膜控制器1作用下的移动机器人巡航速度不随障碍物距离变化, 固定为500 mm/s, 使得机器人前进速度不变(500 mm/s), 在障碍物区域和通道区域, 前进速度快, 机器人反应时间短(分别约为110、120个执行次数, 平均每个执行次数耗时: 0.072 s), 造成碰撞. 死区环境由于左右侧传感器检测值相近, 造成控制律中权值乘累加部分小, 旋转角速度小(最大约正负20度/s), 导致碰撞.

|
图 12 膜控制器1控制下的移动机器人实物结果 |
膜控制器2控制下的实验结果如图14所示: 图14(a)–14(h)为移动机器人通过多障碍物区域的过程, 图14(i)–14(l)为通过通道区域的过程, 图14(m)– 14(p)为避开死区的过程. 从图中可以看出, 膜控制器2控制下的移动机器人顺利避开场景中相隔50 cm的障碍物, 通过80 cm的狭窄通道并避免了与死区环境的碰撞.
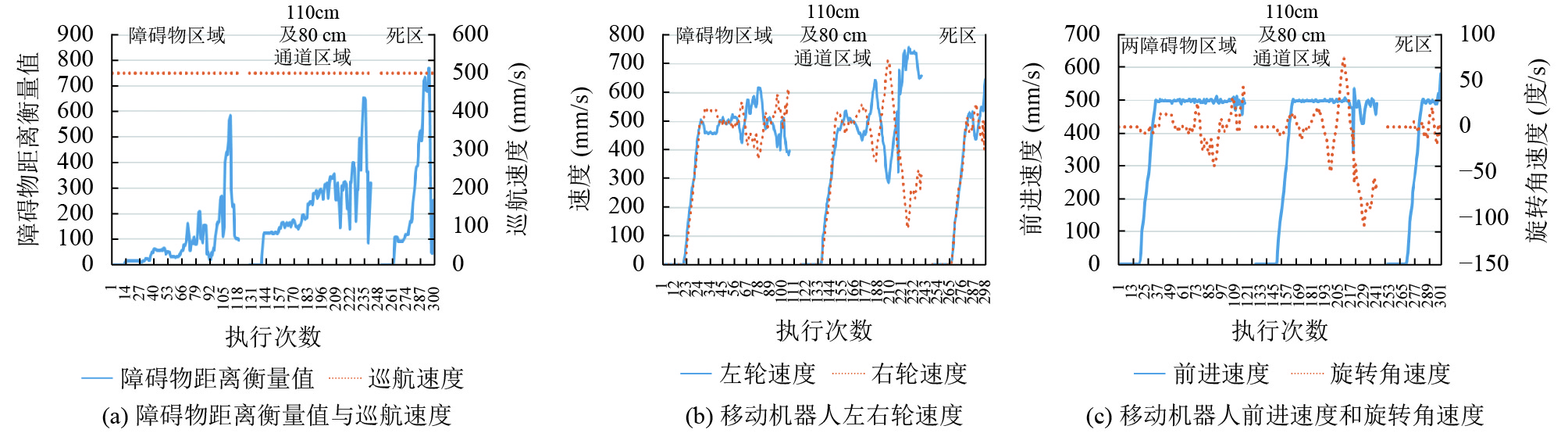
从速度图15可进一步看出: 膜控制器2控制下的移动机器人巡航速度随着障碍物距离的减小而减小, 前进速度变化规律相同. 障碍物区域前进速度降至200 mm/s左右, 通道区域降至100 mm/s左右, 死区降至50 mm/s左右, 使得移动机器人有足够的时间调整姿态(分别约为140、280、160个执行次数, 平均每个执行次数耗时: 0.087 s), 防止与环境相撞.
|
图 13 膜控制器1控制下的移动机器人速度 |

|
图 14 膜控制器2控制下的移动机器人实物结果 |
从上述的仿真和实物实验可以得出: 膜控制器2控制的移动机器人能够随着障碍物与机器人间的距离自适应调节速度, 兼顾了避障效果和速度, 避障控制效果更优.
4 结论本文对基于膜系统的移动机器人避障控制方法进行详细的分析, 总结了一般的参数取法, 分析了传统方法的不足. 针对传统方法无法兼顾避障效果和无障碍物时移动机器人的行走速度, 本文通过使巡航速度随着障碍物与机器人之间的距离自适应改变, 使移动机器人在障碍物近时, 巡航速度降低, 提高避障效果; 障碍物远或无障碍物时, 巡航速度增大, 兼顾了避障效果和移动机器人行走速度. 采用酶数值膜系统设计控制器, 利用多个膜融合多传感器的信息, 根据融合的距离信息调节巡航速度. 仿真实验和实物实验表明: 本文设计的酶数值膜控制器可行且避障控制效果更优.

|
图 15 膜控制器2控制下的移动机器人速度 |
| [1] |
张葛祥, 程吉祥, 王涛, 等. 膜计算: 理论与应用. 北京: 科学出版社, 2015.
|
| [2] |
Pǎun G, Suzuki Y, Tanaka H, et al. On the power of membrane division in P systems. Theoretical Computer Science, 2004, 324(1): 61-85. DOI:10.1016/j.tcs.2004.03.053 |
| [3] |
Bernardini F, Gheorghe M. Cell communication in tissue P systems: Universality results. Soft Computing, 2005, 9(9): 640-649. DOI:10.1007/s00500-004-0393-4 |
| [4] |
Krishna SN. Universality results for P systems based on brane calculi operations. Theoretical Computer Science, 2007, 371(1-2): 83-105. DOI:10.1016/j.tcs.2006.10.016 |
| [5] |
张葛祥, 潘林强. 自然计算的新分支—膜计算. 计算机学报, 2010, 33(2): 208-214. |
| [6] |
Zhang GX, Gheorghe M, Pan LQ, et al. Evolutionary membrane computing: A comprehensive survey and new results. Information Sciences, 2014, 279: 528-551. DOI:10.1016/j.ins.2014.04.007 |
| [7] |
Wang T, Zhang GX, Zhao JB, et al. Fault diagnosis of electric power systems based on fuzzy reasoning spiking neural P systems. IEEE Transactions on Power Systems, 2015, 30(3): 1182-1194. DOI:10.1109/TPWRS.2014.2347699 |
| [8] |
Buiu C, Vasile C, Arsene O. Development of membrane controllers for mobile robots. Information Sciences, 2012, 187: 33-51. DOI:10.1016/j.ins.2011.10.007 |
| [9] |
Ciobanu G, Păun G, Pérez-Jiménez MJ. Applications of membrane computing. Berlin Heidelberg: Springer-Verlag, 2006.
|
| [10] |
Pavel AB, Vasile CI, Dumitrache I. Membrane computing in robotics. Kelemen J, Romportl J, Zackova E. Beyond Artificial Intelligence: Contemplations, Expectations, Applications. Berlin: Springer, 2013. 125-135.
|
| [11] |
Buiu C, Pavel AB, Vasile CI, et al. Perspectives of using membrane computing in the control of mobile robots. Proceedings of Beyond AI-Interdisciplinary Aspect of Artificial Intelligence Conference. Pilsen, Czech Republic. 2011. 22-26.
|
| [12] |
Vasile CI, Pavel AB, Dumitrache I, et al. Implementing obstacle avoidance and follower behaviors on koala robots using numerical P systems. Proceedings of the Tenth Brainstorming Week on Membrane Computing. Sevilla, Spain. 2012. 215-227.
|
| [13] |
Pavel AB, Buiu C. Using enzymatic numerical P systems for modeling mobile robot controllers. Natural Computing, 2012, 11(3): 387-393. DOI:10.1007/s11047-011-9286-5 |
| [14] |
马勤勇. 两轮差速驱动移动机器人运动模型研究[硕士学位论文]. 重庆: 重庆大学, 2013.
|
| [15] |
Lucas GW. A tutorial and elementary trajectory model for the differential steering system of robot wheel actuators. http://rossum.sourceforge.net/papers/DiffSteer/, 2001.
|
 2019, Vol. 28
2019, Vol. 28


