分布式光纤传感周界系统是一种利用光纤随振动后相位变化所引起的一系列物理特性的变化, 进而实现对光路上干扰信号的振动监测, 具有比较高的可靠性. 并且光纤本身也具有抗电磁干扰、抗腐蚀性等优点, 光纤传感已经成为整个周界领域的研究热门方向之一[1].
目前光纤周界方面主要研究的系统结构为Sagnac、OTDR、FB以及单M-Z等, 其中, 研究M-Z结构的特点由于较简易、整体系统硬件成本低、定位算法比较容易实现等优点, 使得该结构在周界领域得到了广泛的应用, 本文通过自己搭建整个实验平台进行数据的采集以及干扰信号的模拟, 再采用LabVIEW软件实现对所采集数据的模拟识别处理以及传感臂和参考臂双路信号的相关性仿真, 根据两路信号时延差信息及相关性强度等实验处理, 进而确定干扰信号类型及外界信号的入侵位置等关键性问题.
1 双M-Z分布式光纤传感周界系统文章主要是利用基于光纤干涉仪原理的光纤传感周界预警和定位系统, 这样的传感系统通常是相位调制型的传感器整个周界系统利用M-Z干涉仪的原理进行实验操作, 该系统主要结构包括光源、光耦合器、光环形器、光电探测器、单模传感光纤等器件组合而成.
在光纤传感系统中, 搭建系统的结构主要采用干涉仪的结构, 具体结构如图1, 其中C1为1×2, C2、C3、C4为2×2的光纤耦合器, 在整个光路中干涉臂的长度大致一样. 光源为长相干光, 光源出来之后经过C1后, 被1: 1的分为两路, 接着其中一路经过2×2的耦合器C2后又被均分为两路, 并且这两路光最后在耦合器C4处发送干涉现象, 这个干涉后的信号通过传感光纤到达耦合器C3处, 其中一路经过光电探测模块D2后, 再通过数据采集卡进入PC; 另外一路光通过耦合器C3进入延时光纤, 然后又通过耦合器C4被分为两路光, 最终在耦合器C2处发生干涉现象, 干涉信号通过其中的一个支路进入光电探测模块D1, 进而通过数据采集卡进入PC. 两个干涉信号最后再PC端进行相应的数据分析处理、模拟识别定位等.

|
图 1 M-Z结构的光纤周界系统原理图 |
2 周界系统的调制原理
整个光纤传感周界系统在没有外界干扰的情况下, 从S发出的光源经过耦合器、传感光纤后在两个光电探测模块D1, D2都能够探测到稳定的干涉信号. 在不考虑外界温度及环境因素的前提下, 我们使用窄带光源, 经过耦合器、干涉仪结构后, 在光电探测模块同样可以检测到比较稳定的光功率.
由于光在传播的过程中相位的变化会和光所传播的距离有关系, 其中单色光的波长为φ, 并且光波通过长为L的传感光纤后会产生相位的延迟, 其中两者之间的关系式如下[2]:
| $ \varphi {\rm{ = }}\frac{{{\rm{2}}\pi n}}{{{\lambda _{\rm{0}}}}}L = \frac{{2\pi }}{\lambda }L = \beta L $ | (1) |
式中, λ0表示光在真空中传播时的波长; β表示光纤的传播系数.
如果在光波传播的过程中外界有干扰, 则干扰行为会直接影响传感光纤的长度、折射率等固定参量的变化, 进而所引起的相位变化关系如下:
| $ \Delta \varphi = \beta \Delta L + L\Delta \beta = \beta L\frac{{\Delta L}}{L} + L\frac{{\partial \beta }}{{\partial n}}\Delta n + L\frac{{\Delta \beta }}{{\Delta r}}\Delta r $ | (2) |
式中, Δφ表示光传播过程中相位的变化, r表示光纤的纤芯半径, n表示光纤纤芯的折射率.
式(2)表示了光波相位发生变化主要是由下述三部分组成[3]: (1) 由于外界因素导致光纤的长度发生变化, 进而造成相位也跟着变化, 这种现象通常称为光纤的应变效应[4]. (2) 这部分主要是因为光纤的折射率的变化所引起的相位变化. 这种变化现象称为光纤的弹光效应[5]. (3) 最后一部分主要是由于光纤的半径变化所引起的相位的变化, 这种现象称为光纤的泊松效应. 最后一部分和前两部分相比而言, 整个光纤的半径、直径的变化是非常微小的, 所以导致的相位变化也是很渺小, 进而可以直接忽略不计[6]. 则外界因素影响下的相位关系式可以简化如下:
| $ \Delta \varphi = \beta \Delta L + L\Delta \beta = \beta L\frac{{\Delta L}}{L} + L\frac{{\partial \beta }}{{\partial n}}\Delta n $ | (3) |
假设耦合器C2到C4之间的两个支路, 支路长为L1, 上面的为传感光纤, 对应的下面支路为参考光纤, C3、C4之间的长度为L2, 若干扰信号在距离耦合器C2的X处, 则两路光波信号从光源到光电探测模块的距离是不同的, 参考光路与传感光路的光路程差为2X, 那么若在D1、D2两端同时进行信号的采集, 则两个信号之间会有一个时间差T, 而造成产生时间差的主要原因就是和外界干扰信号的确切位置有着直接的关系, 所以对光纤传感周界系统的信息分析处理, 应当首先确定干扰信号所发生的位置, 通过计算两路信号所产生的时间差T, 在实际操作中, 对于干扰信号的位置确定主要实现过程如下所述[7]:
即X=(t1c)/n; 则干扰信号距离耦合器C4的距离为:L1−X=(t2c)/n; 耦合器C3、C4之间的距离为: L2=(t3c)/n; 上述各式中c为真空中的光速, n为光纤纤芯的折射率.
因此在光电探测模块D1处所检测到的电信号为:
| $ {y_1}(t) = {I_1}[1 + {Q_1}\cos (\varphi (t - {t_1}) + {\varphi _0}] $ | (4) |
同样在光电探测模块D2处所检测到的电信号为:
| $ {y_2}(t) = {I_2}[1 + {Q_2}\cos (\varphi (t - {t_2} - {t_3}) + {\varphi _0}] $ | (5) |
上述式子中I1和I2分别表示A、B两方向的干涉仪输入光强, Q1和Q2则表示对应的干涉信号的对比度, φ0则为初始相位, 通常情况下默认为π/2, 这个时候整个周界系统的灵敏度是最高的. 而上述y1(t)与y2(t)两者间存在一定的时间差T, 则[8–10]:
| $ T = {t_2} + {t_3} - {t_1} = \frac{{({L_1} + {L_2} - 2X)n}}{c} $ | (6) |
则外界干扰信号的位置为:
| $ X = \frac{{(L1 + L2 - cT/n)}}{2} $ | (7) |
因此只要计算出两路之间信号的时间差T, 就可以准确掌握外界干扰信号的具体位置[11,12]. 两者之间不仅存在时间差, 理论上探测模块D1、D2所接收的信号波形应该基本一致, 因此两个光路信号具有极强的相关性, 我们可以对所得到的两路信号进行一定的相关性计算, 就会得出一个最大值, 此刻便是两个光支路信号相关性信号最强的时候, 将此时所得到的最大值与零时刻的值进行比较, 就会得出两路的信号时间差T, 通过这样的方法也可以判断出外界干扰信号的具体位置.
4 实验的结果及分析 4.1 正交调制的选择提高采用虚拟仪器LabVIEW对系统所采集的数据进行分析处理, 由光纤干涉的条件可以断定, 当两臂信号的相位差为π/2时, 光的干涉效应才能达到最佳状态, 因此进行正交偏置的调制仿真. 如图2.
由该图可以验证, 左下角的图为零偏置和正交偏置两种方式进行的仿真图, 可以明确看出当处于正交偏置状态时, 信号的灵敏度及幅值都有很大程度的提升, 对整个系统测量动态多范围信号具有较好的使用价值.
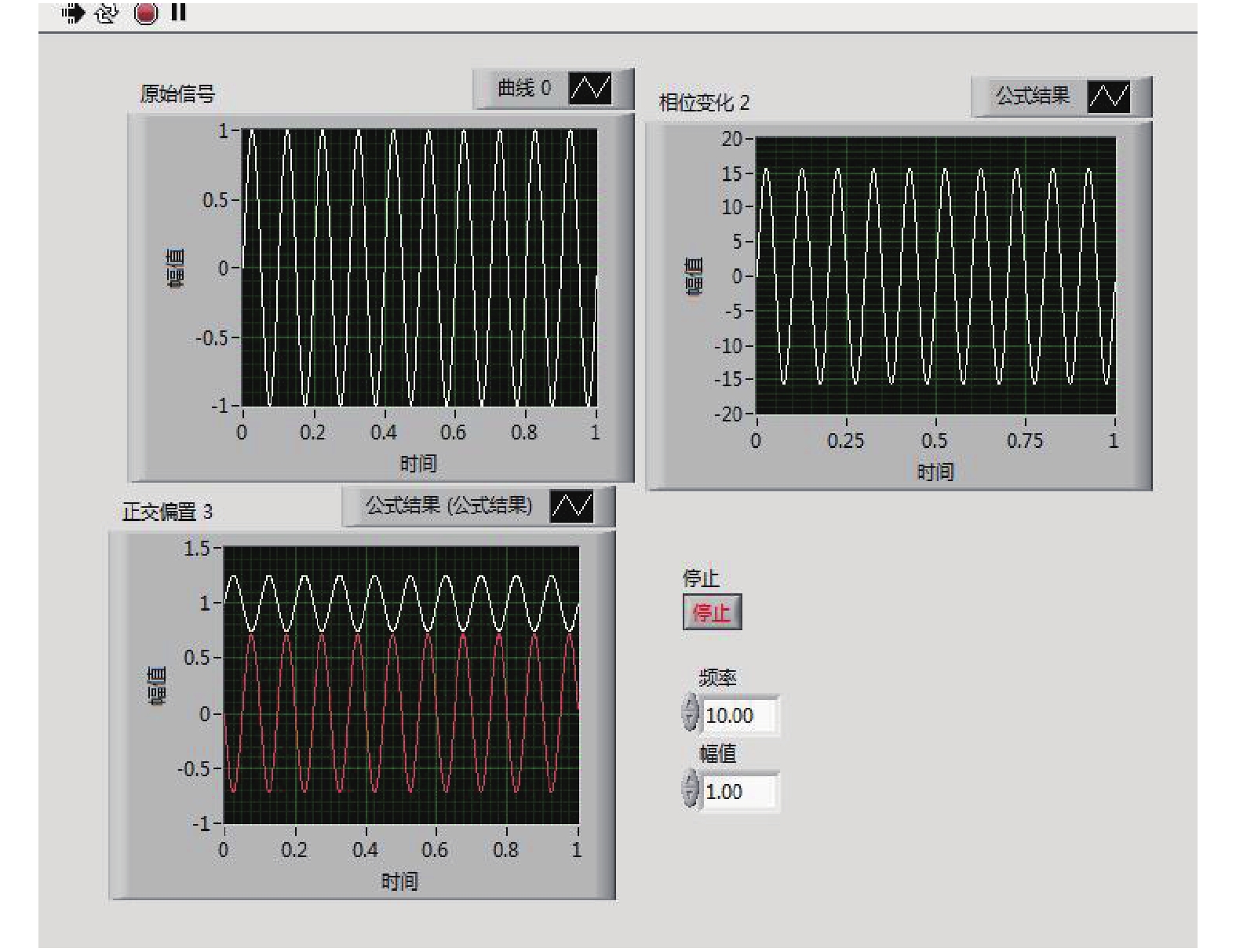
|
图 2 正交偏置仿真 |
4.2 采集信号的模式识别
采用阈值法对干扰信号进行有效的识别处理, 由于整个系统对数据的实时性要求较高, 并且在对外界情况进行监测过程中会产生大量数据, 若对全部数据进行分析, 则会造成较大的运算量, 可能会拖慢系统的进程. 所以采用阈值法对采集信号进行筛选, 进而只对判断为入侵信号的数据进行相关性处理, 有效的提高了系统的运算能力. 具体仿真图如图3至图5所示.
根据阈值法对干扰信号进行信号类型区分辨别, 依据采集的20多组数据的准确分析可以确定常见的几种干扰信号的阈值区间(人为干扰: ≥310; 雨声: 200~310; 风声: 100~200).
针对仿真结果图显示, 阈值法可以准确的判断出干扰信号的类型, 由图3程序的前面板图可以明确看出测量数据的最大值为21.8257, 波形图所显示的时间段波形基本稳定, 类似一般的生活噪声, 所以程序给出正常状态的效应提示. 而图4则是文件路径添加实验环境在有风的情况下测量的数据, 根据软件分析可以在前面板明确看出最大值为146.6, 符合100~200范围内, 所以判断的效应为有风状态. 由图可知所获取的波形图不稳定, 将幅值低于10的基本视为生活噪音, 会存在个别尖峰波形, 是由于外界吹风的原因导致波形突变, 但峰值范围基本稳定, 由于实验环境并不完全隔离, 所以测量范围也比较大, 从而会导致波形的原始正弦信号被淹没, 致使最终波形中看不到原正弦波. 图5所分析的数据集幅值为330.56, 符合之前的人为干扰阈值范围, 所以程序的最终判断效应为人为击打, 从而产生报警响应.

|
图 3 模式识别(正常状态) |

|
图 4 模式识别(有风状态) |

|
图 5 模式识别(人为入侵) |
通过实验的验证, 可以将该周界系统应用到一些区域安防中, 准确率较高, 具有一定的可行性.
4.3 周界系统的定位研究利用采集卡的采集程序进行周界环境的外界信号采集, 并利用软件编程, 实现对外界信号的模式识别后, 进而准确的得出干扰信号的位置信息, 对整个安防事业全能高效的工作起到较高的作用.
由图6可以准确看出右边的图为为被测外界干扰原始信号, 左边为利用软件进行原始信号的解调还原, 进而根据解调得到的信号进行定位确定. 图中也显示了部分位置的一些振幅情况. 图7则是利用双路信号的相关性进行仿真运算, 当噪声水平较低时, 才能实现对相关极大值的索引值得到准确的计算. 两路信号的延时分别为200和800, 即两路信号的时延差为600, 取得互相关函数最大值索引减去采样值得599, 及求得 时间差与信号的真实事件相差一个单位, 因此认为采用此方法进行干扰定位比较可靠.

|
图 6 干扰信号定位程序 |

|
图 7 双路信号互相关程序 |
5 结论
通过实验结果的分析, 可以验证通过使用阈值设定的方法进行干扰信号类型的确定, 这不仅可以提高整体系统的使用效率及运算速度, 还能够减少复杂运算对系统硬件本身的损耗, 节约成本. 同时利用互相关理论实现了对两路信号时延差的准确提取, 进而确定侵入信号的准确位置具有一定的可行性[13–16], 而且通过对系统的改进, 可以将信号的定位误差确定在较小的范围内, 这样一来, 整体的结构设计及研究对实际工程中应用所采用的监测系统, 能够满足其所需的基本干扰识别及侵入定位. 因此, 这样的分布式光纤周界系统在实际应用中对判断干扰异常等事物具有一定的可行性和很大程度的应用价值.
| [1] |
Hu AZ, Rao YJ, Nie ZL, et al. Characteristics of the etched long-period fiber gratings. Acta Photonica Sinica, 2004, 33(8): 916-919. |
| [2] |
Juarez JC, Maier EW, Choi KN, et al. Distributed fiber-optic intrusion sensor system. Journal of Lightwave Technology, 2005, 23(6): 2081-2087. DOI:10.1109/JLT.2005.849924 |
| [3] |
周琰, 靳世久, 曾周末, 等. 分布式光纤管道安全检测定位技术研究. 光电子∙激光, 2008, 19(7): 922-924. |
| [4] |
孙琪真. 分布式光纤传感与信息处理技术的研究及应用[博士学位论文]. 武汉: 华中科技大学, 2008. 33.
|
| [5] |
Hong XB, Wu J, Zuo C, et al. Dual Michelson inter-ferometers for distributed vibration detection. Applied Optics, 2011, 50(22): 4333-4338. DOI:10.1364/AO.50.004333 |
| [6] |
罗光明, 张春熹, 马宗峰, 等. 分布式光纤安防系统传感和定位技术研究. 压电与声光, 2009, 31(3): 327-329, 333. DOI:10.3969/j.issn.1004-2474.2009.03.009 |
| [7] |
姜长东. 连续分布式光纤传感安防系统定位算法的研究[硕士学位论文]. 大连: 大连海事大学, 2013.
|
| [8] |
万遂人, 彭丽成. 安防系统光纤信号特征提取与分类算法研究. 科技导报, 2012, 30(36): 24-28. DOI:10.3981/j.issn.1000-7857.2012.36.002 |
| [9] |
Chen QM, Jin C, Bao Y, et al. A distributed fiber vibration sensor utilizing dispersion induced walk-off effect in a unidirectional Mach-Zehnder interferometer. Optics Express, 2014, 22(3): 2167-2173. DOI:10.1364/OE.22.002167 |
| [10] |
Kim JH, Kwon WS, Lee H, et al. Double-looped Mach-Zehnder interferometer for achieving multiple ring-down interferograms. Optics Express, 2014, 22(23): 28353-28362. DOI:10.1364/OE.22.028353 |
| [11] |
蒋立辉, 张峰, 刘向明. Mach-Zehnder干涉型长周界预警系统入侵目标定位. 传感器与微系统, 2011, 30(4): 48-50. DOI:10.3969/j.issn.1000-9787.2011.04.015 |
| [12] |
聂文伟. 基于LabVIEW的光纤干涉传感信号解调和定位研究[硕士学位论文]. 北京: 北京交通大学, 2008.
|
| [13] |
曾周末, 张溪默, 封皓, 等. 双Mach-Zehnder光纤干涉传感系统中的偏振衰落控制. 光学 精密工程, 2012, 20(3): 468-476. |
| [14] |
仲伟博. 基于典型光纤振动传感器的研究. 内江师范学院学报, 2010, 25(4): 30-33. DOI:10.3969/j.issn.1671-1785.2010.04.008 |
| [15] |
胡晓东, 刘文晖, 胡小唐. 分布式光纤传感技术的特点与研究现状. 航空机密制造技术, 1999, 35(1): 28-31. |
| [16] |
张诚, 王金海, 陈才和, 等. 基于数字信号处理的干涉型光纤传感器检测系统的研究与设计. 传感技术学报, 2007, 20(1): 64-67. DOI:10.3969/j.issn.1004-1699.2007.01.015 |
 2019, Vol. 28
2019, Vol. 28



