1 引言

贝叶斯网络源于概率统计学, 作为数据挖掘和机器学习的重要方法之一, 被人们广泛的应用. 朴素贝叶斯(Naive Bayes)分类方法是贝叶斯网络的简化, 具有坚实的理论基础, 和其他分类方法相比, 展现出高速度和高效率, 被广泛应用于模式识别, 数据挖掘以及机器学习中^[1]. 朴素贝叶斯分类方法基于条件独立性假设, 即假设一个变量对分类的影响独立于其他变量. 当独立性假设成立时, 与其它分类方法相比, 朴素贝叶斯方法理论上具有最小的误分类率. 在实际的应用中, 对于连续变量的数据. 我们通常假设变量服从高斯分布, 通过EM算法求得各个变量所服从高斯分布的均值和方差, 从而可以得到变量不同取值的概率作为后验概率. 再根据贝叶斯定理, 构造朴素贝叶斯分类器, 从而实现对数据分类的结果. 而混合高斯模型GMM是指多个高斯分布函数的线性组合. 理论上, GMM模型可以拟合出任意变量的分布. 使用混合高斯模型代替原有的高斯分布作为变量的概率密度函数, 可以提升连续变量的概率密度拟合效果, 从而改进了朴素贝叶斯分类器对连续型数据的分类能力.

2 朴素贝叶斯 2.1 贝叶斯方法

贝叶斯方法提供了一种通过概率进行推理的手段. 它假定待考查的变量遵循某种概率分布, 且可根据这些概率以及已经观察到的数据进行推理, 从而做出最优的决策^[2–5]. 我们通过贝叶斯定理的公式来介绍这一方法:

$P(h|D) = \frac{{P(h)P(D|h)}}{{P(D)}}$

(1)

当给定训练集合D, 假设空间H中的最有可能假设可以通过贝叶斯公式来计算.

其中, $P(h)$ 表示还没有进行训练前, 假设h拥有的初始概率, 即 $h$ 的先验概率, 它通常根据关于h是一正确假设的概率的背景知识. 在没有先验知识的情况下, 通常可以认为候选假设服从均匀分布, 即把每一个候选假设赋予相同的概率. $P(D)$ 表示将要观察的训练实例集D的先验概率, 即在没有确定某一假设成立时D的概率, 通常可以用全概率公式求出. $P(h|D)$ 表示给定训练实例集D时h成立的概率, 即 $h$ 的后验概率, 通常理解为在看到训练实例集D后, $h$ 成立的置信度.

当变量属性是离散型时, 类的先验概率 $P(h)$ 可以通过训练集的各类样本出现的次数来估计. 当变量属性是连续型时, 有两种方法来估计属性的后验概率 $P(h|D)$ . 第一种方法是把每一个连续的变量属性离散化, 然后用相应的离散区间替换连续属性值, 但这种方法不好控制离散区间划分的粒度. 第二种方法是, 可以假设连续变量服从某种概率分布, 然后使用训练数据估计分布的参数, 高斯分布通常被用来表示连续属性的类条件概率分布.

2.2 朴素贝叶斯

朴素贝叶斯, 简单来说就是对于给出的待分类项, 假设各个属性之间是相对独立的, 求解在此项出现的条件下各个类别的概率最大值. 然后将其归类于所求解出的最大值所属的类别. 在属性相对独立的假设下, 朴素贝叶斯分类器具有简单的星型结构. 每个属性结点只有唯一的父类结点, 这意味着, 当类给定时, 属性之间条件独立^[6].

$P(c|x) = \frac{{P(c)P(x|c)}}{{P(x)}} = \frac{{P(c)}}{{P(x)}}\prod\limits_{i = 1}^d {P({x_i}|c)} $

(2)

其中, $d$ 为属性数目, ${x_i}$ 为 $x$ 在第 $i$ 个属性上的取值.

对于所讨论的所有类别来说, $P(x)$ 都是相同的, 故所得判别准则如下:

$h(x) = \arg \max P(c)\prod\limits_{i = 1}^d {P({x_i}|c)} $

(3)

即, 所判类别为属于赋予先验概率为权重的概率乘积的最大值.

在分类器中, 我们对每个属性条件概率 $ {{P}}\left( {{x_i}|c} \right) $ 的估计是首要的计算部分, 只有求出条件概率才能进行贝叶斯分类的判别^[7]. 在本文中, 我们分别用高斯模型和混合高斯模型来进行概率密度估计, 再构造朴素贝叶斯分类器进行对比.

3 概率密度估计 3.1 高斯混合模型

当贝叶斯分类器选取连续变量的时候, 需要知道各个变量的概率密度函数. 一般情况下, 我们通常假设各个变量服从高斯概率分布. 然而, 测井数据中的各个变量通常不能完全服从高斯概率分布, 拟合效果误差较大. 针对这种情况, 本文考虑使用混合高斯概率模型(GMM)来拟合各个测井数据的概率密度分布.

混合高斯模型的数学模型为:

$f(x) = \sum\limits_{i = 1}^m {{\varepsilon _i} * Guass({\mu _i},{\sigma _i})} $

(4)

其中, ${\varepsilon _i}$ 是表示第 $i$ 个高斯项的权重或者称为混合系数, 且 $\sum\limits_{i = 1}^m {{\varepsilon _i} = 1} $ . $Guass({\mu _i},{\sigma _i})$ 表示高斯密度函数, ${\mu _i}$ 和 ${\sigma _i}$ 分别为高斯密度函数的均值和方差. GMM模型使用的高斯模型的个数称为GMM高斯模型的阶数^[7,8]. 通常情况下, GMM模型进行概率密度估计的阶数不易过大或者过小. 阶数过大会导致参数估计过程难以收敛, 阶数过小会导致参数估计误差较大. 本文考虑选取五阶GMM模型进行概率密度估计.

3.2 EM算法

采用GMM模型进行概率密度估计, 便要对GMM模型中进行参数估计, 通常可以采用极大似然估计法获得参数, 然而极大似然估计需要知道观测数据由哪个高斯分模型产生. 如果不清楚观测数据由哪个分模型产生, 即不确定每个数据所属的分类. 这就意味着需要使用隐变量来进行参数估计, 针对这种情况选取EM算法解决GMM模型的参数估计问题. 本文选取的测井数据并不知道每个数据所属的分类, 所以选取EM算法来估计GMM模型的参数.

EM算法以极大似然估计为基本思想, 采用迭代的方法进行参数估计. EM算法的流程可以分为E步骤和M步骤. 首先要初始化分布参数 $\theta $ ；然后重复E、M步骤直到收敛^[9–11]:

E步骤: 根据参数 $\theta $ 初始值或上一次迭代所得参数值来计算出隐性变量的后验概率(即隐性变量的期望), 作为隐性变量的估计值:

${Q_i}({{\rm{z}}^{(i)}}): = p({z^{(i)}}|{x^{(i)}};\theta ).$

(5)

M步骤: 将似然函数最大化以获得新的参数值:

$\theta : = \arg \mathop {\max }\limits_\theta \sum\limits_i {\sum\limits_{{z^{(i)}}} {{Q_i}({z^{(i)}})\log \frac{{p({x^{(i)}},{z^{(i)}};\theta )}}{{{Q_i}({z^{(i)}})}}} } $

(6)

4 实例分析

研究数据来自苏里格气田41-33区块下古气井的测井曲线. 该地区岩性为复杂的碳酸盐, 主要有7种岩性, 分别是石灰岩、白云质石灰岩、泥质石灰岩、白云岩、灰质白云岩、泥质白云岩和泥岩. 根不同的测井参数及其不同的组合形式可以识别不同的岩性. 选取的测井参数不同, 岩性识别的效果具有很大的差异. 因此, 根据不同测井参数区分不同岩性的敏感性分析^[12,13], 结合人工判别岩性的经验, 最终确定自然伽马(GR), 补偿中子(CNL)、密度(DEN)、声波时差(AC)、光电吸收截面指数(PE)和深侧向电阻率(RLLD)六个测井参数作为朴素贝叶斯分类器的分类属性.

分别选取石灰岩、白云质石灰岩、泥质石灰岩、白云岩、灰质白云岩、泥质白云岩和泥岩各200个样本, 共1400条样本作为测试集. 其中深侧向电阻参数取值范围过大, 结合先前的处理经验, 对其进行对数处理(log10). 对六个测井曲线参数进行量纲化, 避免不同量纲对实验结果造成不良影响. 经过上述处理过的数据, 作为实验的训练集.

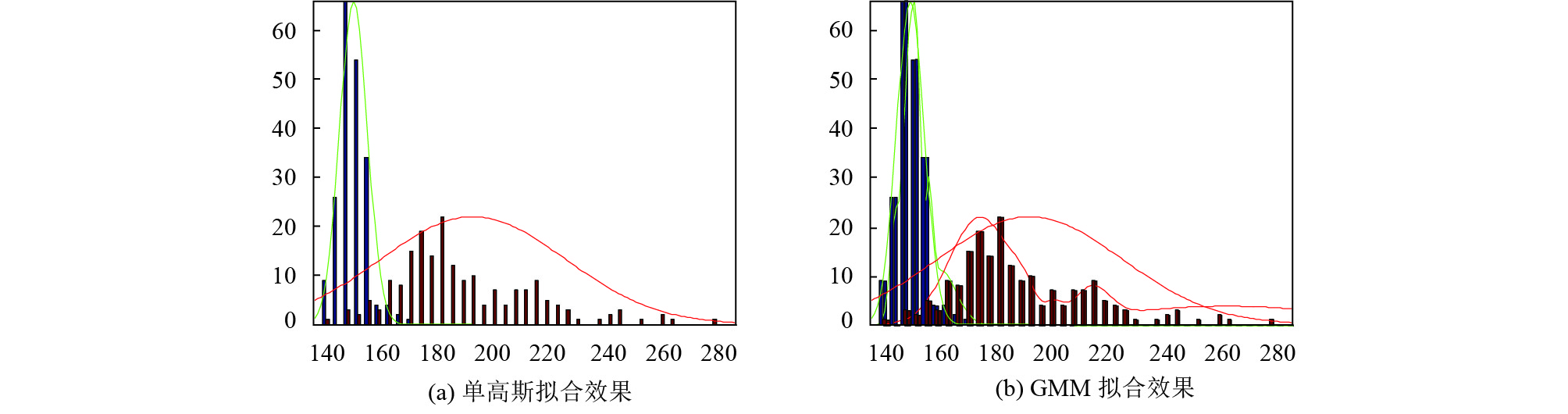
针对实验选用的训练集, 首先分别用高斯模型和混合高斯模型对选取的6个测井参数进行概率密度估计, 然后对比概率密度估计效果. 高斯模型主要是对每种岩性的不同测井参数的均值和方差进行EM算法迭代估计, 得到每种岩性的不同测井参数的均值和方差, 从而得到高斯模型的参数, 以此作为先验信息构造朴素贝叶斯分类器. 而混合高斯模型是用EM算法迭代每种岩性的不同测井参数的均值, 方差以及每个高斯模型的权重, 从而得到混合高斯模型的参数, 并以此作为先验信息构造朴素贝叶斯分类器. 当朴素贝叶斯分类器处理连续属性时, 通常假设连续属性服从某种分布, 这里分别用高斯分布和混合高斯分布作为连续属性的概率密度分布函数. 同时对不同概率密度模型作用下的朴素贝叶斯分类器分类效果作对比, 选训练集中的白云岩和泥岩中的AC测井参数, 来对两种不同的概率密度函数估计效果进行分析, 并根据两种概率密度函数的曲线分析分类器的分类效果. 概率密度估计效果如图1所示.

在图1中, 根据所选取的数据, 左边蓝色直方图和右边红色直方图分别代表了白云岩、泥岩数据真实的分布, 图中绿色和红色的线分别代表白云岩和泥岩的拟合的概率密度曲线, 图1(a)和图1(b)分别为高斯模型拟合效果图和混合高斯模型拟合效果图.

为了更好地比较高斯模型和混合高斯模型的概率密度拟合效果, 引入“误判区”这个概念. 图2给出两个等概率类别的例子, 同时给出了最简单情况下 $x$ 的函数 $p(x|{\omega _i})$ , i=1,2的变化情况. ${x_0}$ 处的虚线是将特征空间分为 ${{R}_1}$ , ${{R}_2}$ 两个区域. 根据贝叶斯决策规则, 对于 ${{R}_1}$ 区域的所有 $x$ 值, 分类器都判定属于 ${\omega _1}$ , 而对于 ${{R}_2}$ 区域的所有 $x$ 值, 都判定属于 ${\omega _2}$ . 但是, 从图中可以判定错误是避免的. 错误率 ${{P}_{\text{e}}}$ 的计算公式为:

$2{P_e} = \int\limits_{ - \infty }^{{x_0}} {p(x|{\omega _2})dx + } \int\limits_{{x_0}}^{ + \infty } {p(x|{\omega _1})dx} $

(7)

式(7)和图2中的阴影部分的面积相等. 因此, 我们把两条概率密度曲线交汇的阴影部分的面积称为误判区^[14].

根据图1, 从概率密度函数的拟合效果上来看, 混合高斯模型拟合的概率密度曲线比高斯模型拟合的概率密度曲线更贴近代表真实分布的直方图. 所以混合高斯模型拟合出来的概率密度曲线更符合测试集数据的真实分布情况. 其次, 两种岩性的测井参数概率密度曲线与坐标轴所围的面积, 分别代表根据AC属性来判断属于白云岩和泥岩的样本. 两条概率密度曲线交汇部分与横轴所围面积代表误判区. 误判区的面积越小, 代表两种岩性基于当前样本的分离度越高. 因此为了提高朴素贝叶斯分类器的分类的准确率, 在选取不同的分布模型拟合样本的真实分布时, 应该选择误判区的面积小的分布模型. 从图1中可以看出, 混合高斯模型中, 绿色和红色两种岩性的概率密度曲线交汇处与坐标轴围成的面积相比于高斯模型来说更小, 因此选用混合高斯模型作为朴素贝叶斯分类器连续属性的分布函数时, 往往能取得更好的分类效果.

对于1400条训练样本, 我们分别采用高斯模型和混合高斯模型的概率密度估计方法对训练集数据进行概率密度估计. 根据EM算法得到的高斯模型均值和方差, 混合高斯模型的均值、方差和权重, 做出不同测井参数的概率密度曲线. 针对估计出的6个测井曲线属性概率密度函数, 构造朴素贝叶斯分类器, 记录训练样本分类的准确率.

图3(a)–图3(f)从左向右分别依次为假设AC、CNL、DEN、PE、GR、RLLD服从高斯概率分布, 采用EM算法迭代估计出来的概率密度函数的均值和方差, 从而做出的概率密度函数的图像.

图4(a)–图4(f)从左向右分别依次为假设AC、CNL、DEN、PE、GR、RLLD服从混合高斯概率分布, 采用EM算法迭代估计出来的概率密度函数的均值、方差以及每个高斯模型的权重, 从而做出的概率密度函数图像.

对比两个图像可以看出, 采用混合高斯概率密度模型估计出的函数模型更符合实际测井曲线资料的真实分布, 具有更好的拟合效果, 不同岩性的测井参数的概率密度曲线交汇部分与横轴所围成的面积更小, 即分类的误判区面积更小. 因此基于GMM模型的朴素贝叶斯分类器分类效果应该更好.

根据估计出来的6个属性的概率密度函数, 构造朴素贝叶斯分类器. 针对1400条训练样本进行训练, 统计分类的正确率, 即岩性识别的正确率, 根据单高斯模型得到的分类正确的样本数为1106, 分类准确率为79%, 根据混合高斯模型得到的分类正确的样本数为1176, 准确率为84%. 可见, 混合高斯拟合的变量概率密度对于朴素贝叶斯分类器的分类准确性有一定的提升.

选取41-33区块下井号为44-45的古气井测井曲线作为测试样本. 选取44-45井的557条测井曲线数据, 同样选取自然伽马(GR), 补偿中子(CNL)、密度(DEN)、声波时差(AC)、光电吸收截面指数(PE)和深侧向电阻率(RLLD)六个属性作为分类指标属性, 其中电阻率仍然进行对数处理(log10). 测试集的岩性识别效果如图5所示.

从图5可以看出, 本次测试使用三种方法进行岩性识别, 钻井岩性代表数据真实的岩性, 7种岩性分别用不同的颜色表示出来, 通过和钻井岩性一列的颜色进行对比, 可以看出岩性识别效果的优劣. 分别采用中心距离判别法, 高斯模型的朴素贝叶斯和GMM模型的朴素贝叶斯三种方法进行测试. 根据钻井岩性对比三种方法的识别结果, 通过对比三种方法识别结果和钻井岩性的颜色可以看出, 采用中心距离判别法进行岩性识别的效果较差, 因为只根据测井数据的均值来进行分类, 选择距离均值距离最近的类别作为分类的类别, 误判区较大. 而传统朴素贝叶斯岩性识别效果要远优于中心距离判别法, 主要是因为在概率密度曲线拟合的过程中, 考虑了均值和方差共同的影响效果, 因而岩性识别效率得到了提升. 基于混合高斯模型的朴素贝叶斯分类器分类效果比传统朴素贝叶斯效果分类更好, 主要因为在概率密度拟合的过程中, 相比于高斯模型, 混合高斯模型能够更好地拟合测井数据的实际分布, 减小分类的误判区, 因而所得到的岩性识别效率最高.

5 总结

本文提出了一种基于EM和GMM的朴素贝叶斯分类器模型用于岩性识别. 通过对测井曲线参数对不同岩性的敏感度分析, 选取了AC, CNL, DEN, PE, GR, RLLD六个参数作为朴素贝叶斯的分类变量. 通过EM算法进行参数迭代, 使用混合高斯模型来拟合每个分类变量的真实概率分布, 构建贝叶斯分类器, 从而实现岩性识别. 相比于传统朴素贝叶斯分类器, 混合高斯模型比高斯模型具有更好的拟合效果, 不同岩性之间的误判区也更小. 在训练集样本中基于混合高斯模型的朴素贝叶斯分类器岩性识别准确率为84%, 传统朴素贝叶斯分类器的准确率为79%, 因此基于混合高斯模型的朴素贝叶斯分类器可以提升分类器的分类效果. 但是, 用于构建朴素贝叶斯分类器的变量现实中并不是完全独立的, 这会影响分类器的分类效果. 若想得到更好的分类效果, 可以借助一些专家经验, 预估各个分类变量之间的条件依赖, 或者通过贝叶斯网络结构学习算法构建贝叶斯网络, 用贝叶斯网络进行分类, 这样岩性识别的准确率会进一步提升.