2. 河南思维信息技术有限公司, 郑州 450000;
3. 株洲中车时代电气股份有限公司, 株洲 412001;
4. 成都运达科技股份有限公司, 成都 611731
2. Henan Thinking Information Technology Co. Ltd., Zhengzhou 450000, China;
3. Zhuzhou CRRC Times Electric Co. Ltd., Zhuzhou 412000, China;
4. Chengdu Yunda Technology Co. Ltd., Chengdu 611731, China
北斗定位技术结合GIS (Geographic Information System, 地理信息系统)电子地图是一种对机车实现远程跟踪和定位的新手段, 目前铁路机务管理信息系统中的核心基础子系统—中国机车远程监测与诊断系统(Chinese locomotive remote Monitoring and Diagnosis system, CMD系统)即基于机车实时下发的北斗数据, 利用GIS技术实现了对机车的远程跟踪和定位, 对机务人员实时掌控机车位置、安全指挥调度都具有十分重要的意义.
目前CMD系统中已注册和谐型机车近7000台, 覆盖全路18个铁路局集团公司, 每台机车均配备机车车载综合信息监测装置(简称LDP), LDP实时向地面发送机车当前的北斗数据, 大量的北斗数据为实现新建铁路线的绘制提供了必要的条件. 目前国内在利用GPS(Global Positioning System, 全球定位系统)及北斗定位数据生成轨道电子地图方面已有许多研究, 如文献[1]提出一种带关键点约束条件的多轨迹求径算法, 利用车站中很多固定的POI点(Points of Interest), 如信号机、道岔、转辙机等, 结合低精度的GPS数据来生成精度较高的站内数字电子地图; 文献[2]提出一种在地图多尺度分层结构的基础上, 采用多点加权检验和Kalman估计差值检验进行错误数据剔除, 利用三次B样条曲线拟合反算生成轨道电子地图; 文献[3]提出一种改进的多轨迹融合算法, 利用两个固定的高精度端点, 从起点到终点不断画圆, 利用局部非线性优化的方法来生成高精度的轨迹. 以上算法研究虽具备一定的参考价值, 但考虑到CMD系统中北斗数据下发的特殊性且并无固定的高精度点, 造成部分机车定位偏移或定位成孤点的现象, 因此以上研究并不能满足CMD系统生成新建铁路地图数据的需求, 为此我们提出一种基于Kalman滤波算法和分段曲线拟合方法对经纬度数据进行处理的思想, 用于提高铁路线绘制的准确性, 精确定位机车位置和轨迹具有重要的现实意义.
1 北斗卫星定位技术介绍北斗技术作为我国独立自主研发的全球定位与导航技术, 不仅对国防安全意义重大, 在民用领域的应用也越来越得到广泛的使用. 据统计, 2017年卫星导航与位置服务产业总产值达到2550亿元, 较2016年增长约20.4%. 并且随着北斗组网建设和北斗二号区域的稳定运行, 预计2023年北斗相关产业规模将达到4600亿元[4].
考虑到铁路运输在国家安全方面的战略地位, 从保证国家信息安全角度出发, CMD系统使用北斗技术而非GPS技术. 北斗技术在CMD系统中的应用主要有两个方面. 一是利用北斗导航技术全天候、全天时定位机车位置, 实时掌握全路机车运行动态, 为故障机车救援提供精确定位. 二是由于北斗链路具备抗干扰能力强、抗衰落能力强、支持高速移动设备、保密性强等优点, 使用北斗短报文通信技术将机车关键业务数据发送到地面, 作为无线通信链路的重要数据补充.
CMD系统车载子系统通过北斗模块获取到机车实时定位信息, 通过CMD系统的4G通道和北斗短报文通道将机车定位信息发送到地面系统中, 为实现机车轨道电子地图生成提供数据支撑. 车载子系统经纬度获取和短报文发送流程如图1所示.
2 研究方法 2.1 基于Kalman滤波法的野值数据剔除数据滤波是去除噪声还原真实数据的一种数据处理技术, Kalman滤波在测量方差已知的情况下能够从一系列存在测量噪声的数据中, 估计动态系统的状态. 由于它便于计算机编程实现, 并能够对现场采集的数据进行实时的更新和处理, 因此Kalman滤波是目前应用最为广泛的滤波方法, 在通信、导航、制导与控制等多领域得到了较好的应用[5,6]. 下面我们基于CMD数据库中导出的经纬度数据集研究利用Kalman滤波进行数据处理的程序算法实现[7].
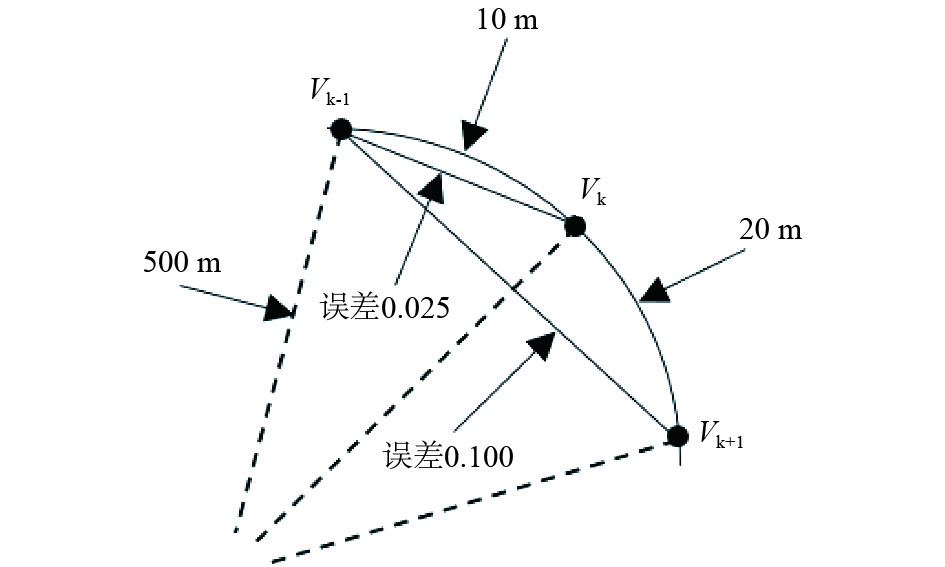
铁路线路的平面由直线、圆曲线及缓和曲线等规则曲线组成, 且曲线半径比较大, 当2个定位点距离较近时, 曲线路段可以近似视为1条直线[8]. 例如图2示, 在曲线半径为500 m的弯股路段, 利用直线近似曲线的原理, 机车从Vk−1运行至Vk, 运行距离约10 m时产生的最大误差为0.025 m; 列车从Vk−1运行至Vk+1, 运行距离约20 m时产生的最大误差为0.100 m. 由此可见, 直线、圆曲线和缓和曲线均可由相邻定位点的位置预测下一个定位点的位置. 因此, 利用Kalman滤波算法, 建立基于轨道几何特征的Kalman预测方程, 可以实现对北斗数据集中野值数据的判断和剔除.
假设机车当前的定位点为Vk, 根据系统模型, 可以基于上一定位点Vk−1的位置预测定位点Vk的位置, 即:
| $ {{{X}}_{\left( {{{k}}|{{k}} - 1} \right)}} = {{A}}{{{X}}_{\left( {{{k}} - 1|{{k}} - 1} \right)}} + {{B}} $ | (1) |

|
图 1 经纬度获取发送流程 |
|
图 2 曲线段近似直线段示意图 |
式中, X(k|k−1)为先验估计值, 表示定位点Vk的位置预测值; X(k−1|k−1)为后验估计值, 表示定位点Vk−1的位置最优值; A和B为由定位点Vk−1和Vk−2的位置最优值获得的线性方程的参数.
用P表示协方差, 则X(k|k−1)的协方差可以表示为:
| $ {{{P}}_{\left( {{{k|k}} - 1} \right)}} = {{A}}{{{P}}_{\left( {{{k}} - 1{{|k}} - 1} \right)}}{{{A}}^{{\rm{T}}}} + {{Q}} $ | (2) |
式中, P(k−1|k−1)为X(k−1|k−1)对应的协方差; Q为经验值, 表示过程噪声的方差, 本文取Q=0.1.
令Zk为利用机车下发的GPS经纬度实际值, 再结合系统预测值即可得到定位点Vk的位置最优估计值X(k|k)为:
| $ {{{X}}_{\left( {{{k|k}}} \right)}} = {{{X}}_{\left( {{{k|k}} - 1} \right)}} + {{{K}}_{{{{g}}_{\left( {{k}} \right)}}}}\left( {{{{Z}}_{\left( {{k}} \right)}} + {{{X}}_{\left( {{{k|k}} - 1} \right)}}} \right) $ | (3) |
其中,
| $ {{{K}}_{{{{g}}_{\left( {{k}} \right)}}}} = \frac{{{{{P}}_{\left( {{{k|k}} - 1} \right)}}}}{{{{{P}}_{\left( {{{k|k}} - 1} \right)}} + {{R}}}} $ | (4) |
式中, Kgk为Kalman增益; R为经验值, 表示测量噪声的方差, 本文取R=0.1.
更新X(k|k)对应的协方差为
| $ {{{P}}_{\left( {{{k|k}}} \right)}} = \left( {1 - {{{K}}_{{{{g}}_{\left( {{k}} \right)}}}}} \right){{{P}}_{\left( {{{k|k}} - 1} \right)}} $ | (5) |
根据以上Kalman滤波算法, 运用式(1)可以由上一定位点Vk–1的位置估算出当前定位点Vk的位置, 结合当前定位点Vk位置的实际测量值Z(k), 再运用式(3)可得到当前定位点Vk位置的最优估值X(k|k). 当实际测量值Z(k)偏差很大, 通过最优估值X(k|k)可以修正偏差, 剔除野值Z(k). 对式(1)至式(5)编写计算机程序, 通过程序的自回归运算可以实现对整条线路定位点中野值的剔除.
2.2 基于分段曲线拟合的轨道地图绘制经过Kalman滤波处理后得到的经纬度数据集, 剔除了部分野值数据, 提升了铁路线绘制的准确性, 为了进一步逼近真实铁路线, 我们对处理后的经纬度数据进行分段曲线拟合, 然后对每一分段计算经纬度点到拟合曲线的垂直距离, 实现经纬度数据集的进一步处理, 最后再将处理后的数据集与地图线路数据集进行融合, 完成地图线路图层数据的添加.
前面提到铁路线是由直线、圆曲线和缓和曲线组成, 要实现铁路线路的曲线拟合, 就需要对Kalman滤波后的数据进行分段并确定相应的拟合类型, 为此我们采用角度差法进行处理, 具体做法是通过建立线路直角坐标系, 利用等间隔算法对Kalman滤波后的数据进行采样, 将采样的经纬度坐标点转换为直角坐标系下的点并在坐标系中标出, 计算采样点i与采样点i+1连成的直线与横轴的夹角θi, 如果采样点落在直线上, 则夹角θi保持不变, 如果采样点落在圆曲线上, 则θi值的变化值∆θi保持不变, 其他的点可认为落在缓和曲线上, 利用这一性质可实现对待拟合的铁路线进行分段并确定相应的拟合曲线类型, 下面分别针对直线、圆曲线和缓和曲线拟合的最小二乘法进行介绍说明.
2.2.1 直线拟合设直线方程为: y=ax+b, 根据直线上的经纬度点数据集(x1, y1), (x2, y2), …, (xk, yk), 由最小二乘原理, 可求得a、b的值分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {{{a}} = \dfrac{{\mathop \sum \nolimits_{{i}} {{x}}_{{i}}^2\mathop \sum \nolimits_{{i}} {{{y}}_{{i}}} - \mathop \sum \nolimits_{{i}} {{{x}}_{{i}}}{{{y}}_{{i}}}\mathop \sum \nolimits_{{i}} {{{x}}_{{i}}}}}{{{{k}}\mathop \sum \nolimits_{{i}} {{x}}_{{i}}^2 - {{\left( {\mathop \sum \nolimits_{{i}} {{{x}}_{{i}}}} \right)}^2}}} = {{\bar y}} - {{b\bar x}}}\\ {{{b}} = \dfrac{{{{k}}\mathop \sum \nolimits_{{i}} {{{x}}_{{i}}}{{{y}}_{{i}}} - \mathop \sum \nolimits_{{i}} {{{x}}_{{i}}}\mathop \sum \nolimits_{{i}} {{{y}}_{{i}}}}}{{{{k}}\mathop \sum \nolimits_{{i}} {{x}}_{{i}}^2 - {{\left( {\mathop \sum \nolimits_{{i}} {{{x}}_{{i}}}} \right)}^2}}} = \dfrac{{\overline {{{xy}}} - {{\bar x\bar y}}}}{{\overline {{{{x}}^2}} - {{{{\bar x}}}^2}}}} \end{array}} \right. $ |
根据上式对各点坐标值进行一次计算就可求出a、b, 即可得到目标直线方程.
2.2.2 圆曲线拟合根据圆曲线上的经纬度点(x1, y1), (x2, y2), …, (xk, yk), 设r为圆曲线半径, (x0, y0)为圆心点坐标, 运用最小二乘法进行圆曲线拟合, 各经纬度点残差平方和函数为:
| $ {{Q}} = \mathop \sum \limits_{{{i}} = 1}^{{k}} {\left[ {{{\left( {{{{x}}_{{i}}} - {{{x}}_0}} \right)}^2} + {{\left( {{{{y}}_{{i}}} - {{{y}}_0}} \right)}^2} - {{{r}}^2}} \right]^2} $ |
根据最小二乘原理有:
| $ \dfrac{\partial Q}{\partial x_0}= \dfrac{\partial Q}{\partial y_0}= \dfrac{\partial Q}{\partial r}=0 $ |
由以上两式可得:
| $ \left\{ \begin{array}{l} {{r}} = \sqrt {{{{x}}_0}^2 - 2{{\bar x}}{{{x}}_0} + {{{y}}_0}^2 - 2{{\bar y}}{{{y}}_0} + \overline {{{{x}}^2}} + \overline {{{{y}}^2}} } \\ {{{x}}_0} = \dfrac{{\left( {\overline {{{{x}}^2}} {{\bar x}} + {{\bar x}}\overline {{{{y}}^2}} - \overline {{{{x}}^3}} - \overline {{{x}}{{{y}}^2}} } \right)\left( {{{{{\bar y}}}^2} - \overline {{{{y}}^2}} } \right) - \left( {\overline {{{{x}}^2}} {{\bar y}} + {{\bar y}}\overline {{{{y}}^2}} - \overline {{{{y}}^3}} - \overline {{{{x}}^2}{\rm{y}}} } \right)\left( {{{\bar x\bar y}} - \overline {{{xy}}} } \right)}}{{2\left( {{{{{\bar x}}}^2} - \overline {{{{x}}^2}} } \right)\left( {{{{{\bar y}}}^2} - \overline {{{{y}}^2}} } \right) - 2{{\left( {{{\bar x\bar y}} - \overline {{{xy}}} } \right)}^2}}}\\ {{{y}}_0} = \dfrac{{\left( {\overline {{{{x}}^2}} {{\bar y}} + {{\bar y}}\overline {{{{y}}^2}} - \overline {{{{y}}^3}} - \overline {{{{x}}^2}{{y}}} } \right)\left( {{{{{\bar x}}}^2} - \overline {{{{x}}^2}} } \right) - \left( {\overline {{{{x}}^2}} {{\bar x}} + {{\bar x}}\overline {{{{y}}^2}} - \overline {{{{x}}^3}} - \overline {{{x}}{{{y}}^2}} } \right)\left( {{{\bar x\bar y}} - \overline {{{xy}}} } \right)}}{{2\left( {{{{{\bar x}}}^2} - \overline {{{{x}}^2}} } \right)\left( {{{{{\bar y}}}^2} - \overline {{{{y}}^2}} } \right) - 2{{\left( {{{\bar x\bar y}} - \overline {{{xy}}} } \right)}^2}}} \end{array} \right. $ |
其中,
常用的缓和曲线方程属于三次抛物线型, 其表达式为:
| $ {{y}} = \frac{{{{{x}}^3}}}{{6{{R}}{{{l}}_0}}} $ |
其中, (x, y)为缓和曲线上任意一点坐标, R为圆曲线半径, l0为缓和曲线的长度. 该方程的坐标原点是直缓点. 对缓和曲线采用三次多项式拟合, 足以保证轨道地图的精度要求. 根据缓和曲线上的经纬度点(x1, y1), (x2,y2), …, (xk, yk), 拟合方程为:
只需要4个数据点的值就可确定上式中的 a、b、c、d 参数的值.
通过编写程序很容易根据经纬度数据集获取到以上三类拟合曲线的参数值, 得到拟合曲线方程后对每一分段计算由定位点到拟合曲线的垂直距离, 可进一步将偏离较远的经纬度点去除, 最后将处理后的经纬度点集追加到地图线路图层数据集中, 利用地图部署工具对相应区域进行切图发布即完成地图的更新.
2.3 基于CMD系统中北斗定位数据的列车轨道电子地图绘制过程由2.1和2.2节中提出的列车轨道电子地图生成算法, 可以将绘制过程概括为5步:
(1)数据采集, 从CMD数据库中导出缺失铁路线路的经纬度数据集;
(2)数据处理, 利用Kalman滤波算法对导出的数据集进行滤波处理, 剔除数据野值;
(3)曲线拟合, 对滤波处理后的数据集等间隔采样、分段, 确定曲线拟合类型, 利用最小二乘法编制Matlab曲线拟合程序进行分段曲线拟合, 得到曲线拟合参数;
(4)数据融合, 根据拟合曲线对滤波后的数据集进行二次处理, 去除偏离拟合曲线较远的离散点, 将处理后的数据集与地图中的线路图层数据集进行融合;
(5)地图发布, 利用地图部署工具对地图重新发布, 完成地图数据的更新.
3 实例分析为了验证基于Kalman滤波算法和分段曲线拟合方法对数据处理的合理性和有效性, 我们采取陇海铁路线上巩义站至上街站区间内的一段铁路线进行实例说明. 系统硬件环境为云存储服务器, 操作系统为Windows Server 2008, 北斗定位数据存储在MongoDB数据库中, 保存至少6个月的机车定位信息.
图3是根据从CMD系统数据库中导出原始经纬度数据在地图中的打点情况显示. 可以看出, 由于机车下发的经纬度数据存在位置浮动, 造成数据点在地图中定位后呈现出局部比较杂乱的状态, 如果不进行数据处理, 那么绘制出来的铁路线必然存在较大的误差.

|
图 3 原始经纬度点集定位显示 |
基于本文中介绍的Kalman滤波算法和分段曲线拟合方法, 通过编写Matlab滤波程序对原始经纬度点集进行Kalman滤波处理, 选取某一段包含直线、圆曲线和缓和曲线的路段作算例, 测量点数据按50 m等间隔采样, 共选取测量点248个, 通过角度差法对路段进行分段, 利用Matlab拟合程序对以上3种线形进行拟合, 计算得到圆曲线半径和缓和曲线长度等曲线参数, 对同一组数据多次分段拟合处理, 对拟合结果进行误差计算结果显示, 拟合出的线路参数不存在较大的偶然误差和系统误差, 符合精度需求. 将经过Kalman滤波和分段曲线拟合处理后的点集在地图中定位如图4所示,数据呈现出较为平滑的状态.

|
图 4 经过Kalman滤波和分段曲线拟合处理后的点集定位显示 |
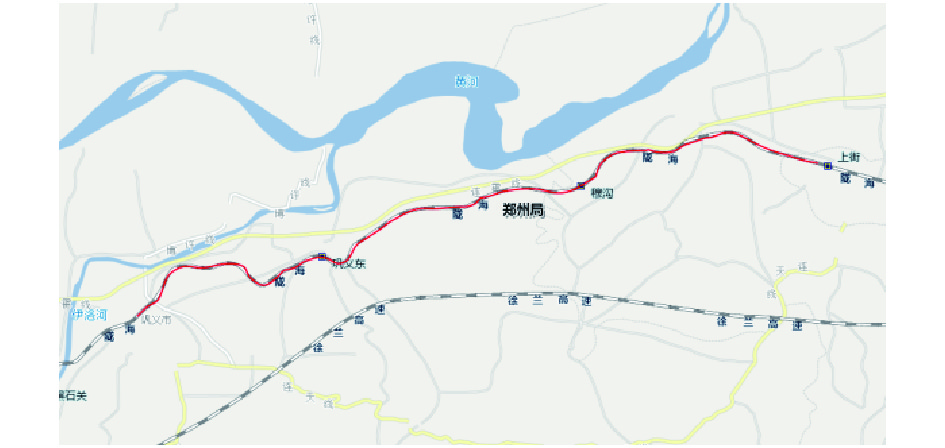
图5是基于Kalman滤波和分段曲线拟合处理后的经纬度数据绘制的铁路线, 可以看出, 生成的线路走势与真实的铁路线基本吻合, 精度较高, 准确性较好, 满足实际应用的需求.
|
图 5 最终生成的轨道线路走势 |
利用本文卡尔曼滤波和分段曲线拟合方法进行地图铁路线生成, 与文献[9]提出的基于稳定估计的几何距离准则拟合铁路线参数的方法进行比较, 后者利用每一次拟合之后的改正数大小来确定权值, 从而逐步减小粗差对拟合精度的影响. 基于上述陇海线巩义站至上街站间机车记录的原始北斗定位数据进行拟合误差计算, 其中离差和为各个数据点的纵坐标与拟合结果的差值的平方和, RMS为该误差的均方根, 它们从统计规律上体现了数据拟合结果的质量. 如表1所示.
| 表 1 方法对比分析结果 |
由表1可知, 本文的Kalman滤波法相比文献[9]的稳定估计加权法对异常定位数据处理效果上更优越, 剔除的异常数据点更多, 处理后的定位点分布趋势更平滑. 本文利用角度差法对定位数据进行分段, 同样比文献[9]利用几何距离法分段更精细, 直线分段数较少, 拟合误差更小, 更逼近真实铁路线走势.
4 结束语本文基于CMD系统中机车下发的北斗定位数据, 提出利用Kalman滤波和分段曲线拟合的方法来生成机车轨道电子地图, 有效地提高了地图线路绘制的准确性, 该方法利用计算机程序对数据实现自动处理, 速度快、效率高、人工参与少, 能够较为准确的实现地图缺失铁路线的绘制, 具备一定的应用价值.
| [1] |
刘嘉, 穆建成, 蔡伯根. 多轨迹GPS数据生成高精度列车控制用数字电子地图的方法. 铁道通信信号, 2007, 43(5): 52-55. DOI:10.3969/j.issn.1000-7458.2007.05.023 |
| [2] |
刘江, 蔡伯根, 唐涛, 等. 基于GPS的列控轨道地图数据生成方法研究. 测绘学报, 2011, 40(1): 111-117. |
| [3] |
杨诗颖, 陈德旺, 曾翔宇. 基于局部优化的多轨迹信息融合算法研究. 第十一届中国不确定系统年会、第十五届中国青年信息与管理学者大会论文集. 邯郸, 中国. 2013. 5.
|
| [4] |
曲向芳. 北斗卫星导航定位系统全球组网产业链迎来新发展机遇——《2018中国卫星导航与位置服务产业发展白皮书》发布. 卫星应用, 2018(8): 65-71. |
| [5] |
Huang YL, Zhang YG, Wang XD. Kalman-filtering-based in-motion coarse alignment for odometer-aided SINS. IEEE Transactions on Instrumentation and Measurement, 2017, 66(12): 3364-3377. DOI:10.1109/TIM.2017.2737840 |
| [6] |
Wang DJ, Lv HF, Wu J. In-flight initial alignment for small UAV MEMS-based navigation via adaptive unscented Kalman filtering approach. Aerospace Science and Technology, 2017, 61: 73-84. DOI:10.1016/j.ast.2016.11.014 |
| [7] |
董绪荣, 陶大欣. 一个快速Kalman滤波方法及其在GPS动态数据处理中的应用. 测绘学报, 1997, 26(3): 221-227, 267. |
| [8] |
倪晓林, 杨妮, 张东. 列控数字轨道地图自动生成算法研究. 铁路运营技术, 2010, 16(1): 24-27. |
| [9] |
朱文华, 覃爱丽. 基于几何距离准则拟合铁路线路参数的研究. 铁路计算机应用, 2010, 19(5): 14-16. DOI:10.3969/j.issn.1005-8451.2010.05.005 |
 2019, Vol. 28
2019, Vol. 28



