燃气负荷数据的预测是燃气系统项目决策的重要指标, 国内外许多学者在这方面做了大量的研究[1–9]. 从文章中可以看出, 神经网络算法是目前运用最为广泛的短期燃气负荷预测方法, 神经网络算法从结构上可以分为前馈型和反馈型神经网络两种. 虽然, 前馈型神经网络包括BP神经网络、RBF神经网络等在短期燃气负荷预测上取得了良好的效果[3,6], 但是, 由于燃气负荷数据受历史负荷数据的影响较大, 要求预测算法可以保存之前的训练结果, 前馈型神经网络不能解决该类问题. 反馈型神经网络RNN (Hopfield网络、Elman神经网络以及Jordan神经网络), 因其反馈之前状态的结构, 具有一定的记忆能力, 能够更好地提取燃气数据的特征. 学者们将反馈型神经网络用于负荷预测上, 并与前馈型网络进行了大量的实验对比研究[8–11], 这奠定了反馈型神经网络处理短期燃气负荷预测的基础.
上述神经网络在结构上都是浅层结构, 浅层结构算法具对于复杂问题, 其泛化能力较差, 存在梯度消失的问题. 2006年Hinton G等人提出了深度学习的框架, 表达了多隐层的人工神经网络与浅层神经网络相比具有优异的特征学习能力, 学习得到的特征对数据有更本质的刻画, 从而有利于可视化或分类. 文献[12]分析了浅层结构在处理电力负荷预测问题时的不足, 对于多维时间序列预测, 将RNN扩展到深度学习中在目前的研究中得到了较好的实验结果[13–15]. 然而, 对于序列很长的数据, RNNs存在梯度消失的问题. 为了解决这个问题, 学者们提出了一些改进的RNNs模型, LSTM和GRU神经网络是目前较为常见的两种. 它们在结构上增加了忘记单元, 比RNNs多了选择记忆的能力, 有效地改善了RNNs梯度消失的问题. LSTM算法是1997年被提出, 用于语言处理方面的研究, 近年, 在电力负荷预测方面运用较多[13,16]. 但因其复杂的网络结构, 需要训练很长时间[14], 为了减少训练时间, 本文选择以GRU神经网络作为燃气负荷预测算法, 将LSTM与GRU进行仿真实验, 证明GRU在燃气负荷预测上的先进性.
由于燃气负荷数据随极端天气与节假日的影响, 这些特殊的日负荷值与相邻时刻的负荷相差较大, 在这些点的预测误差较大. 学者们尝试将数据进行信号分解, 将数据按频率分成若干分量来解决这个问题. 文献[17,18]以LMD算法与RNN结合处理时间序列预测, 证明LMD算法与反馈神经网络结合的可行性与优越性. LMD算法是一种新型的具有自适应性的信号分解方法, 它将原始数据分解为一系列的PF分量, 这些分量是由纯调频信号与包络信号相乘得到, 可以保证其瞬时频率是正的、连续的, 具有一定的物理意义. 为了提高预测精度, 本文采用LMD算法与GRU神经网络结合来预测短期燃气负荷值.
LMD算法利用滑动平均法得到局部均值函数与包络函数, 相比于其它方法, 滑动平均法的端点效应不明显, 但是同样会有过平滑的问题. 文献[18]用Akima插值方法优化LMD算法, 成功的解决了LMD过平滑的问题, 依照这样的思路, 在本文中, 同样对LMD算法的插值方法做改进. 文献[19]详细比较了几种常用的插值方法, 可以看出牛顿插值法计算较为简单, 且在处理过平滑方面优于其它几种插值方法, 本文将利用牛顿插值法代替LMD的滑动平均值法来获得局部均值函数和包络估计函数, 改善传统LMD方法存在的过平滑问题.
负荷数据在采集过程中需要人工参与和调整, 负荷值不可避免的存在一部分噪声数据. 噪声数据一般处于数据的高频部分, 对预测精度影响较高, 本文使用小波阈值去噪方法对PF分量进行处理, 对高频与低频数据分别处理, 可以有效提高了去噪能力. 文献[20–23]分析了小波阈值去噪的阈值选择问题以及阈值函数的改进方法, 本文将根据实际数据实验情况选择合适的阈值函数, 用改进后的小波阈值去噪方法对LMD的PF分量去噪. 文献[24]中提出利用小波阈值去噪方法对LMD的PF分量进行去噪处理, 通过实验证明了对PF分量去噪的优越性. 综上所述, 本文首先使用牛顿插值方法改进LMD算法同时对LMD分量进行小波阈值去噪处理, 之后将改进的LMD算法(WT-LMD)与GRU神经网络结合作为短期燃气负荷预测的方法.
1 改进的LMD算法 1.1 LMD算法局部均值分解(Local Mean Decomposition, LMD)算法是一种自适应时频分析方法, 它将非平稳信号分解成若干个不同频率的PF分量和一个余量, 每个PF分量的瞬时频率和频幅可以很好的反映信号的时频特征. 对于任意的非平稳信号X(t), 具体分解步骤如下:
(1) 找出X(t)的所有局部极值点, 包括极大极小值点, 对两个相邻的极值点ni, ni+1求平均值.
(2) 将所有的平均值点连接起来, 利用滑动平均法得到局部均值函数m11(t), 并将m11(t)从X(t)中分离: h11(t)=X(t)–m11(t).
(3) 求出相邻极值点的包络估计值ai:
| ${{{a}}_i} = \frac{{\left| {{n_i} - {n_{i + 1}}} \right|}}{2}$ |
同样将所有的ai连接起来, 利用滑动平均法进行平滑处理得到包络估计函数a11(t).
(4)对h11(t)解调得到:
判断s11(t)是否为纯调频信号, 即满足|s11(t)|≤1; 若不是, 将s11(t)作为新的原始信号重复上述步骤, 迭代n次, 直至s1n(t)为纯调频信号, 即其包络估计函数a1(n+1)(t)=1.
(5)将迭代过程中的a11(t), …, a1n(t)相乘得到包络信号a1(t), 将a1(t)与s1n(t)相乘即为第一个PF分量PF1(t). PF1(t)是信号中频率最高的部分, 它的瞬时频幅就是a1(t), 瞬时相位为φ(t)=arccos(s1n(t)), 瞬时频率f1(t):
(6)从X(t)中分离出PF1(t)得到: μ1(t)=X(t)–PF1(t), 将μ1(t)作为新的原始信号重复上述步骤, 得到相应的PF2(t)和μ2(t). 如此, 迭代n次, 直到μn(t)是一个单调函数, 结束循环.
(7)原始信号X(t)可表示为这n个PF分量的和加上μn(t):
| $X\left( {\rm{t}} \right) = \sum\limits_{i = 1}^n {P{F_i}\left( t \right) + {\mu _n}\left( t \right)} $ |
通过局部均值分解(LMD)方法将燃气负荷数据分解为不同频域下的分量, 上述计算这些分量过程中, 由于分量的瞬时频幅和频率都可以通过计算获得, 使得分量具有一定的物理意义, 可以很好的看出燃气负荷的潜在特征. 但是, 在实际操作过程中, LMD算法在处理序列较长的数据时, 若滑动跨度选择不当, 会引起函数不收敛导致过平滑问题, 或者表现为分解的分量过多, 使得分量失去价值. 为了解决这一问题, 本文提出利用牛顿插值法代替滑动平均法优化LMD算法.
1.2.1 牛顿插值法对于一组数据:
n0(x0, f(x0)), n1(x1, f(x1)), …, nk(xk, f(xk))构建牛顿插值多项式:
N(x)=f(x0)+(x–x0)f(x0, x1)+…+f(x0, x1, …, xk)Пik−1(x–xi)
式中f(x0, x1, …, xk)是函数f(x)的k阶差商, 即:
| ${f}\left( {{x_0}, {x_1}} \right) = \frac{{f\left( {{x_0}} \right) - f\left( {{x_1}} \right)}}{{{x_0} - {x_1}}}$ | (1) |
| ${f}\left( {{x_0}, {x_1}, {x_2}} \right) = \frac{{f\left( {{x_0}, {x_1}} \right) - f\left( {{x_1}, {x_2}} \right)}}{{{x_0} - {x_2}}}$ | (2) |
| $ {f}\left( {{x_0}, {x_1}, \cdots, {x_k}} \right) = \frac{{f\left( {{x_0}, \cdots, {x_{k - 1}}} \right) - f\left( {{x_0}, \cdots, {x_k}} \right)}}{{{x_0} - {x_k}}} $ | (3) |
由式(3)可以看出每阶差商都可由前一阶差商推出, 得到各阶差商, 按照插值多项式就可以计算出插值点的值.
1.2.2 小波阈值去噪小波阈值去噪的原理就是原始信号进行小波变换后得到的含有噪声的小波系数w, 有效信号在空间或时间上具有连续性, 所以幅值较大. 而噪声信号是随机的, 往往处于高频区域, 所以设置合适的阈值, 就可以将含噪声的小波系数去除留下有效系数w’. 去噪过程如图1.

|
图 1 小波阈值去噪 |
燃气负荷数据在采集过程中由于人为调整或者管网系统的故障问题不可避免地会产生一些异常数据即噪声数据, 针对这个问题, 通常使用小波阈值去噪方法对原始燃气负荷数据进行去噪处理. 但是, 燃气负荷数据具有随机性, 数据波动较大, 很难选择合适阈值, 从而影响去噪效果和预测精度.
1.2.3 改进的LMD算法在1.1介绍了传统局部均值分解算法的过程, LMD算法利用滑动平均法确定局部均值函数和包络估计函数, 从而计算出PF分量. 实验过程中, 为了解决这个问题, 采用牛顿插值法代替滑动平均法对LMD算法进行改进. 牛顿插值法与其它插值法相比, 结构简单, 且敏感度相对较低, 平滑效果相比滑动平均法较差, 可以有效解决过平滑问题[19].
原始数据通过局部均值分解得到一系列的由高频到低频的PF分量, 这些分量存在一定的噪声数据, 高频区噪声较多, 影响预测效果. 本文利用小波阈值去噪方法对这些PF分量数据进行去噪处理, 相比于对直接原始负荷数据直接去噪, 在不同频域内分别选择适当的阈值, 进行小波阈值去噪可以有效地提高去噪能力. 流程如图2所示.

|
图 2 改进的LMD算法 |
2 GRU神经网络 2.1 GRU网络结构
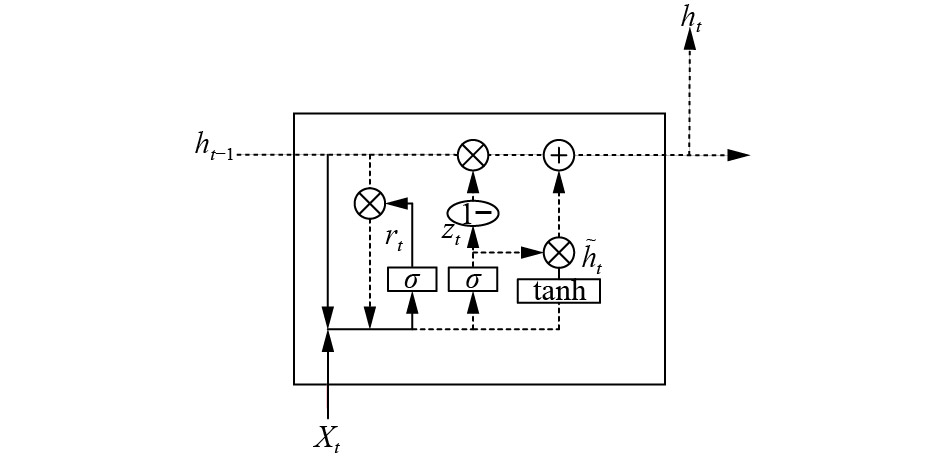
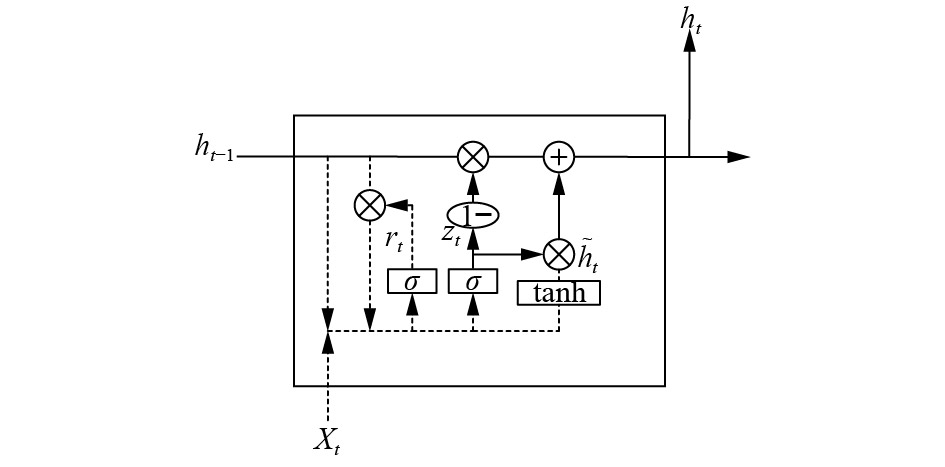
GRU神经网络包含两个门单元(更新门z和重置门r), 结构如图3所示. 更新门控制上一时刻的信息用到当前时刻中的程度, 更新门的值越大表示上一时刻对当前时刻的影响越高. 重置门控制忘记上一时刻信息的程度, 重置门的值越小表示上一时刻对当前时刻的影响越少.

|
图 3 GRU神经网络 |
隐藏状态h利用更新门控制之前时刻隐藏状态与当前时刻的候选隐藏状态结合更新的程度. 如果, 在时间t1到t2之间的状态一直近似1. 那么, t1到t2之间的信息几乎没有输入到当前时刻的隐藏状态. 这个设计有利于更好地捕捉时间序列中时间间隔较长数据对当前时刻的影响程度.
候选隐藏状态
上图中状态与输出的计算如下:
| $ {{z}_t} = \sigma ({W_z} \cdot \left[ {{h_{t - 1}},{x_t}} \right]) $ | (4) |
| $ {{r}_t} = \sigma ({W_r} \cdot \left[ {{h_{t - 1}},{x_t}} \right]) $ | (5) |
| $ {{\tilde h}_t} = \tanh (W \cdot \left[ {{r_t} \cdot {h_{t - 1}},{x_t}} \right]) $ | (6) |
| $ {{h}_t} = \left( {1 - {z_t}} \right) * {h_{t - 1}} + {z_t} * {\tilde h_t} $ | (7) |

|
图 4 zt |
|
图 5 rt |

|
图 6 |
|
图 7 ht |
2.2 LMD与GRU网络组合算法
本文提出一种将LMD算法与GRU神经网络组合的方法, 用于预测短期燃气负荷值. 由于燃气数据的波动性较大, 本文选取2013年的燃气负荷值, 进行局部均值分解可以得到9个PF分量, 如图8和图9所示. 再将这些分量进行小波阈值去噪(图10显示PF1的去噪结果)之后, 分别以各分量作为输入数据构建GRU网络分别进行预测. 最后, 将所有预测结果相加得到负荷的预测值, 具体流程如图11.
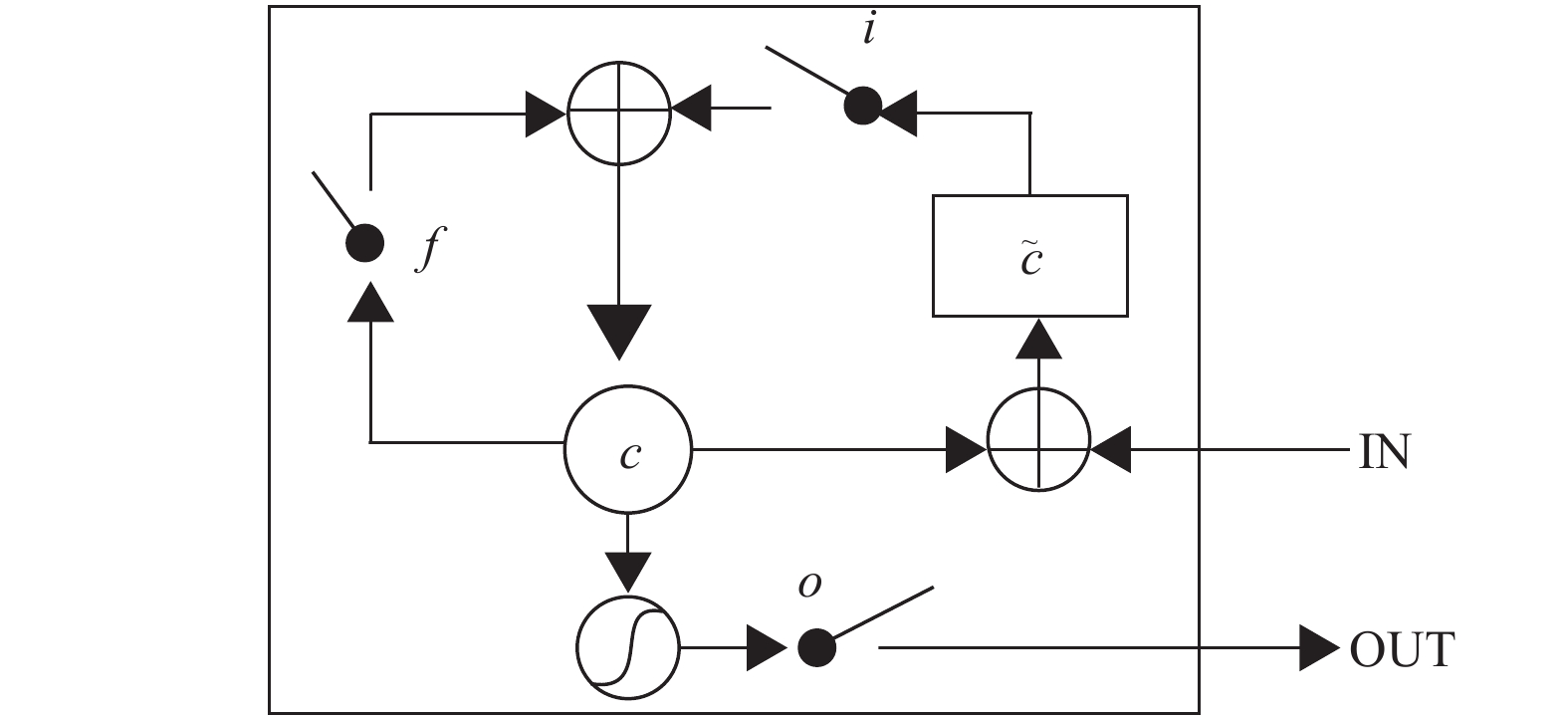
3 GRU与LSTM神经网络GRU与LSTM在结构上十分的相似, 都是为了解决RNN的长期依赖问题设计的门控单元结构. LSTM包含三个门函数(输入门、忘记门和输出门), 如图12所示, 而GRU模型仅仅包含两个门函数(重置门和更新门). 如果将重置门全部设置为1, 并且更新门设置为0, 就退化为RNN模型. 显而易见, 由于少了输出门的计算, GRU网络参数更少, 训练速度更快. 而当实验数据较多时, LSTM网络效果更好.
GRU神经网络与LSTM在实验结果上相差不大, 需根据实际数据选择适当的模型[18]. 本文将2005年到2014年的燃气负荷作为输入数据(数据未处理), 选取2000个数据做训练数据, 1000个作为测试数据. 分别以GRU和LSTM两个模型进行预测, 结果如图13和图14为两种模型的误差曲线以及预测值曲线. 可以看出预测精度两者相差不大, MAPE分别为0.0217和0.1988,
GRU神经网络的收敛速度更快. 为了减少训练时间, 本文选用GRU神经网络作为负荷的预测算法.
4 实验对比为了验证本方法的先进性, 以上海实际燃气2010-2013每年的真实负荷值作为实验数据, 将其划分成300个训练数据和65个测试数据. 在进行预测之前, 对数据采用LMD算法进行信号分解, 得到图8和图9所示的9个分量, 提高了数据的平滑性.
之后, 对这些PF分量进行小波阈值去噪处理得到有效的分量数据. 将这些分量数据归一化到(0, 1)之间, 并将它们进行划分. 本文采用MATLAB与python两种编程语言实现模型的构建. 用MATLAB实现局部均值分解以及小波阈值去噪部分的处理, 之后将得到的数据导入python进行预测操作, 调用Keras里的深度学习包对神经网络进行建模. 为了检验本方法的预测效果, 将该方法与单一的GRU神经网络以及未进行去噪处理的组合算法进行对比, 采用平均绝对误差MAE、平均绝对百分比误差MAPE以及均方根误差RMSE作为评价指标.
分别采用GRU、LMD-GRU、WT-LMD-GRU方法对测试数据进行预测, 预测结果见图15. 其中, 虚线表示真实负荷, 其它曲线分别表示利用上述3种预测模型预测得到的负荷预测值曲线. 图中可以看出:
(1) LMD-GRU算法的拟合度高于单GRU网络;
(2) WT-LMD-GRU网络的拟合度高于LMD-GRU算法.

|
图 8 原始负荷曲线 |

|
图 9 PF分量 |
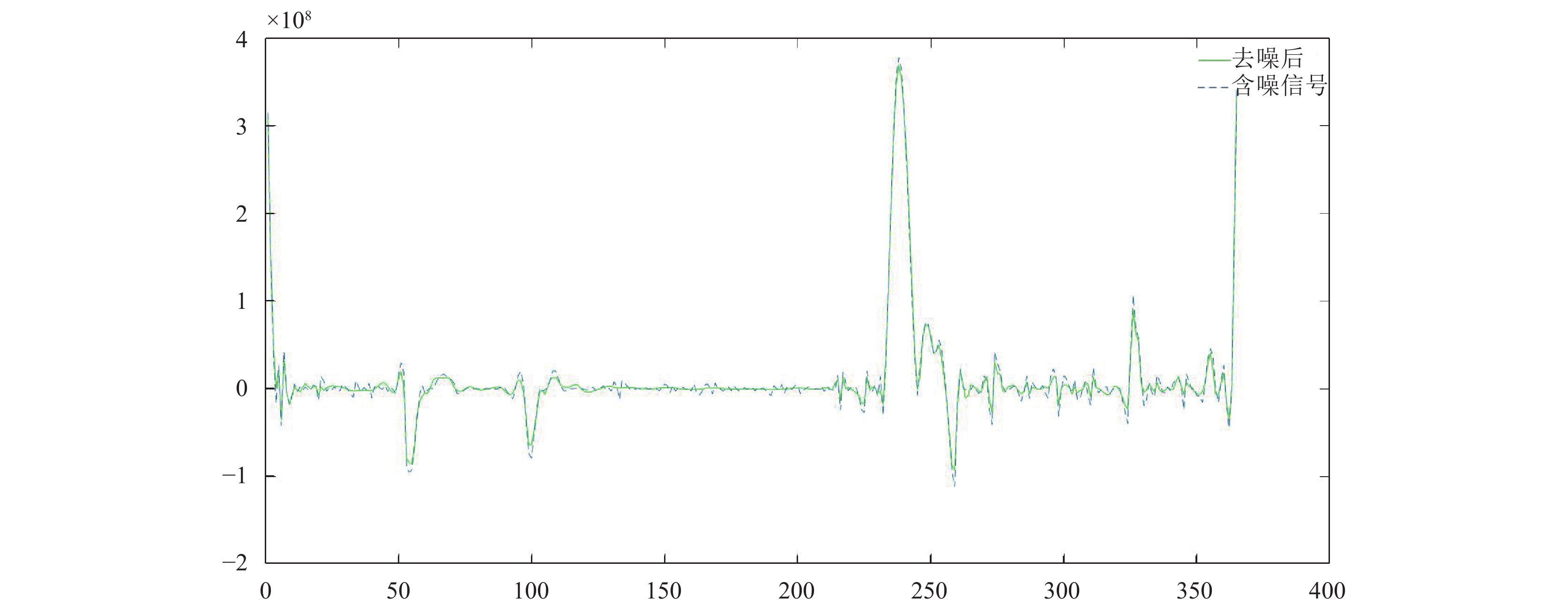
|
图 10 小波去噪 |
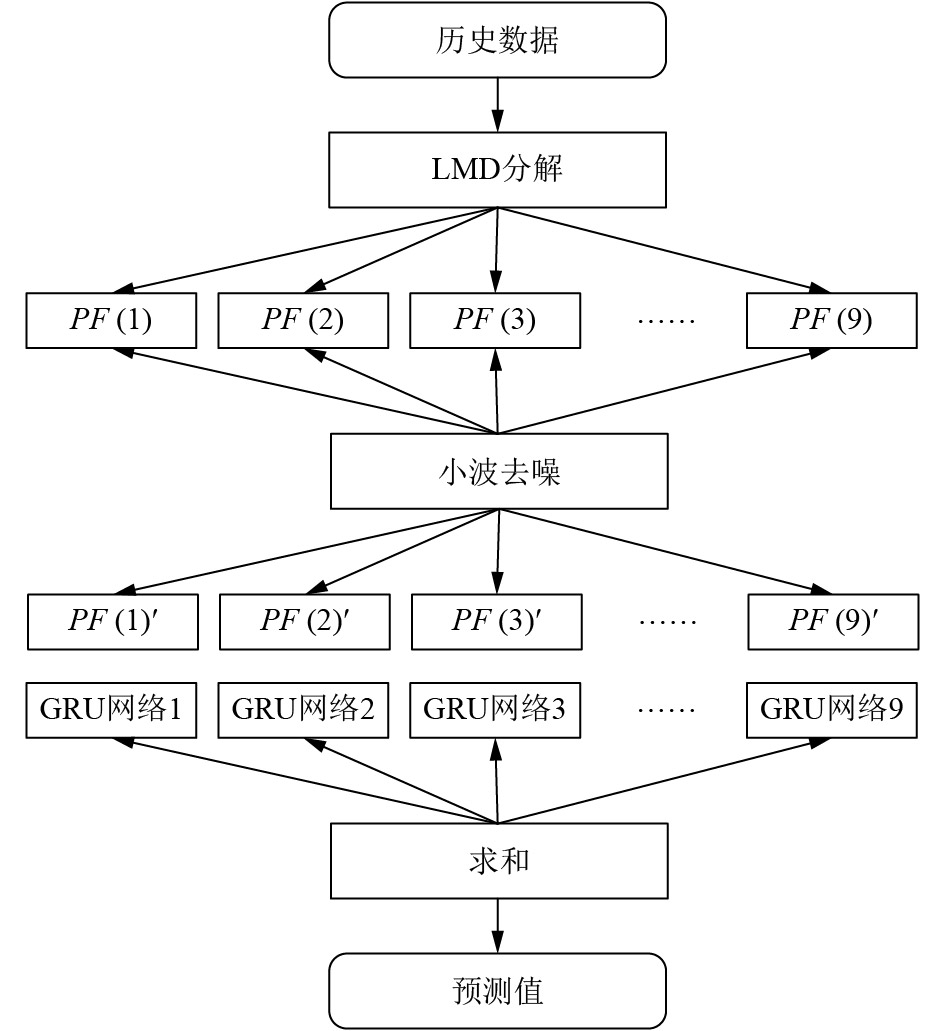
|
图 11 LMD与GRU组合模型 |
在运算时间上, 由于单独对各个PF分量分别构建网络进行训练, 训练时间相比单一的GRU网络直接预测负荷较长. 在算法复杂度方面, 改进的LMD算法和小波阈值去噪计算简单, 对于整个预测模型来说影响不大.
将三种方法的预测值与实际值的误差根据评价指标, 如表1所示: 表中可以看出本文提出的方法在预测精度上高于传统算法. 表中将LMD算法与GRU神经网络结合比单一的GRU网络预测精度更好, 图8中可以看出LMD算法将原始数据从高频到低频的信号分解处理, 让数据更加平滑, 更容易学习数据的潜在特征. 然而, 由于噪声数据的影响, 导致数据在高频去的预测效果较差, 影响整体预测精度, 利用小波阈值去噪对PF分量进行处理, 使得阈值的确定较为容易, 有效数据含量更高, 预测效果更好.
|
图 12 LSTM结构 |
5 结论与展望
本文提出一种改进的LMD算法与GRU神经网络结合的短期燃气负荷预测方法, 该方法利用牛顿插值法代替滑动平均法改进LMD算法, 对负荷数据进行分解, 避免了传统算法过平滑的问题. 之后, 利用小波阈值去噪对分解出的PF分量进行去噪处理, 研究表明, 在分解后去噪比分解去噪的效果更好, 阈值函数的确定更为简单. 最后, 将处理后的PF分量分别输入GRU网络中进行预测, 将所有预测结果相加得到最终预测值.

|
图 13 LSTM与GRU的收敛速度对比 |

|
图 14 LSTM与GRU精度对比 |

|
图 15 3种模型对比 |
| 表 1 预测误差指标 |
通过实验对比分析, 本文提出的方法较传统方法具有优越性, 预测精度更高. 但是, 该方法同样存在训练时间长, 参数多的问题. 在之后的研究中, 重点将放在网络参数优化以及多维输入可行性方向.
| [1] |
Qu SL, Ma F. Prediction of macro city gas load on BP neural network theory. Proceedings of the 5th International Conference on Computer Science & Education. Hefei, China. 2010. 538–542.
|
| [2] |
Chen HL, Wang ZY, Yu P. Study on combination forecasting of gas daily load based on the generalized dynamic fuzzy neural network. Proceedings of the 33rd Chinese Control Conference. Nanjing, China. 2014. 6235–6239.
|
| [3] |
Yu F, Xu XZ. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Applied Energy, 2014, 134: 102-113. DOI:10.1016/j.apenergy.2014.07.104 |
| [4] |
Yang Z, Liu Y, Miao ZB, et al. Application of neural-network in natural gas load forecasting. Gas & Heat, 2003, 23(6): 331-332, 336. |
| [5] |
杨昭, 金国民, 苗志彬. 基于模糊-RBF BP神经网络的天然气负荷预测. 暖通空调, 2005, 35(3): 96-99. |
| [6] |
Ding ZQ. Application of RBF neural network to gas load forecasting. Gas & Heat, 2013, 33(5): 43-46. |
| [7] |
Wang JS, Zhu QW. Short-term electricity load forecast performance comparison based on four neural network models. Proceedings of the 27th Chinese Control and Decision Conference. Qingdao, China. 2015. 2928–2932.
|
| [8] |
Musilek P, pelikán E, Brabec T, et al. Recurrent neural network based gating for natural gas load prediction system. Proceedings of 2006 IEEE International Joint Conference on Neural Network Proceedings. Vancouver, BC, Canada. 2006. 3736–3741.
|
| [9] |
宋超, 宋娟, 任军. 基于Elman神经网络的短期天然气负荷预测建模与仿真. 工业控制计算机, 2016, 29(4): 87-88. DOI:10.3969/j.issn.1001-182X.2016.04.040 |
| [10] |
Zhang ZS, Gong WJ. Short-term load forecasting model based on quantum Elman neural networks. Mathematical Problems in Engineering, 2016, 2016: 7910971. |
| [11] |
陈亚, 李萍. 基于神经网络的短期电力负荷预测仿真研究. 电气技术, 2017, 18(1): 26-29. DOI:10.3969/j.issn.1673-3800.2017.01.006 |
| [12] |
董浩, 程鹏, 李玲玲. 深度学习算法在电力系统短期负荷预测中的应用. 电气时代, 2017(2): 82-84. |
| [13] |
陈亮, 王震, 王刚. 深度学习框架下LSTM网络在短期电力负荷预测中的应用. 电力信息与通信技术, 2017, 15(5): 8-11. |
| [14] |
Fu R, Zhang Z, Li L. Using LSTM and GRU neural network methods for traffic flow prediction. Proceedings of the 31st Youth Academic Annual Conference of Chinese Association of Automation. Wuhan, China. 2016. 324–328.
|
| [15] |
Shao HX, Soong BH. Traffic flow prediction with long short-term memory networks (LSTMs). Proceedings of 2016 IEEE Region 10 Conference. Singapore. 2016. 2986–2989.
|
| [16] |
Chen Z, Sun LX. Short-term electrical load forecasting based on deep learning LSTM networks. Electronic Technology, 2018, 47(1): 39-41. |
| [17] |
雷庆坤, 李生虎, 陈曦鸣, 等. 基于改进的LMD和GRNN组合风速预测. 合肥工业大学学报(自然科学版), 2015, 38(7): 891-896. DOI:10.3969/j.issn.1003-5060.2015.07.006 |
| [18] |
邹红波, 伏春林, 喻圣. 基于Akima-LMD和GRNN的短期负荷预测. 电工电能新技术, 2018, 37(1): 51-56. |
| [19] |
俞海军, 陈瑾怡. 三种插值方法的研究与比较. 河南科技, 2013(20): 210-211. |
| [20] |
刘卫东, 刘尚合, 胡小锋, 等. 小波阈值去噪函数的改进方法分析. 高电压技术, 2007, 33(10): 59-63. DOI:10.3969/j.issn.1003-6520.2007.10.014 |
| [21] |
唐圣学, 付滔, 李志刚. 基于自适应小波阈值去噪和HT-LMD的电能质量扰动检测方法. 电测与仪表, 2017, 54(17): 70-76. DOI:10.3969/j.issn.1001-1390.2017.17.013 |
| [22] |
王旭. 改进小波阈值法在变形监测数据处理中的应用. 测绘与空间地理信息, 2018, 41(1): 83-85. DOI:10.3969/j.issn.1672-5867.2018.01.022 |
| [23] |
郑尊凯, 文畅, 谢凯, 等. ELMD联合粒子群优化小波阈值的语音去噪研究. 长江大学学报(自科版), 2018, 15(1): 33-38. DOI:10.3969/j.issn.1673-1409.2018.01.007 |
| [24] |
刘涛涛, 潘宏侠. 应用改进的LMD和小波降噪于滚动轴承故障诊断. 噪声与振动控制, 2014, 34(2): 152-157. DOI:10.3969/j.issn.1006-1335.2014.02.035 |
 2019, Vol. 28
2019, Vol. 28



