在工业生产中, 集成电路芯片的制造包括生产、探测、装配和测试环节[1–3]. 在测试过程中, 需要将半导体芯片置于高温烤箱中进行耐温测试以检测出潜在的风险. 为了提高测试效率, 芯片被分成不同的批次集中放在烤箱中处理. 这里, 半导体芯片就类似于工件, 烤箱类似于机器. 这是一个典型的批处理机调度的例子.
批调度问题不同于传统的机器加工问题,一个批处理机能同时加工处理多个工件, 从而有效提高资源的利用率. 研究批调度问题, 通过优化调度有效提高生产效率, 降低生产成本, 对于提高生产管理水平、获取更高的经济效益有着重要的现实意义[4].
人们对批调度问题的研究由来已久. Gimple和Ikura[5]最先研究了工件尺寸相同、到达时间和交货期相一致的单机批调度问题. Lee和Uzsoy[6]提出了动态规划的方法来解决此类调度问题, 优化目标是最小化最大延迟时间和最小化延迟工件数, 局限性在于这种基于动态规划的精确求解方式需要较长的计算时间. Uzsoy[7]首次将工件尺寸相同的性质扩展到差异工件. 在此基础上, Zhou[8]融入了工件动态到达的限制, 并结合距离矩阵提出了构造性启发式算法, 这些一次性启发式算法在处理大规模工件问题时虽然在运行时间上占优, 但解的质量并不太好.
在实际生活中, 工厂往往采用多台机器并行处理的方式来提高生产效率. Chang[9]、Damodaran和Chang[10]等考察了并行批处理机调度问题, 优化目标是最小化制造跨度. 其中Chang采用模拟退火算法, 通过交换初始解中不同批中的工件生成邻域解, 这导致初始解的质量对最终解的质量有很大影响, 从而影响算法的性能. Chen[11]在并行机基础上纳入了动态到达的约束, 并结合蚁群算法和遗传算法以及ERT-LPT规则来优化完工时间, 并且取得了不错的效果.
元启发式算法也被越来越多的学者应用到调度问题中. 例如基于构建性的蚁群算法[12], 基于邻域搜索的模拟退火算法[3,9]和进化算法,其中进化算法包含但不限于遗传算法[13]、粒子群算法[14]、差分进化算法[15]等. 分布式估计算法作为一种较新的基于种群的进化算法, 在求解组合优化问题方面具有良好的表现, 比如置换流水车间问题[16], 护士排班问题[17], 但是在并行机调度方面的应用研究却很有限. 因此, 本论文采用分布式估计算法求解考虑差异工件的并行批处理机调度问题.
论文组织如下: 第1章节为问题描述; 第2章节详细介绍分布式估计算法在考虑差异工件的并行批处理机调度中的应用; 第3章节为仿真实验; 第4章节为结论与展望.
1 问题描述 1.1 数学模型论文考虑包含差异工件的并行批处理机调度问题, 相关假设如下:
(1) 将n个工件分配到m个批处理机加工;
(2) 工件具有不同的尺寸和加工时间;
(3) 各台机器容量一致, 工件j只需在其中一台机器上加工, 且它在所有机器上加工时间相同;
(4) 工件集中分批, 按照批次顺序安排在机器上加工;
(5) 批的尺寸等于批中所有工件尺寸之和, 且不能超过机器容量限制, 批的加工时间等于批中工件最大加工时间;
(6) 一旦某个批次开始加工, 加工过程不能中断且不能有新的工件加入到当前批中;
(7) 优化目标是makespan, 也就是使最后离开加工 系统的批次的完工时间最小;
该问题采用调度理论中的三元组法[18]可表示为Pm|batch, B, sj|Cmax, 以下给出相关参数定义及混合整数规划模型:
① 集合
工件集合:
批集合:
机器集合:
② 参数
sj: 工件j尺寸;
pj: 工件j加工时间;
B: 机器容量;
③ 决策变量
PTbk: 在机器k上加工的批b的加工时间;
CTbk: 批b在机器k上的完工时间;
Cmax: 最终完工时间;
xjbk: 工件j分在批b中安排在机器k上加工时为1, 否则为0;
数学模型如下:
| $ Minimise\;\;\;\;\;\;\;\;\;{C_{\max }} $ | (1) |
| $ {\rm{s.t.}}\;\;\sum\limits_{b = 1}^n {\sum\limits_{k = 1}^m {{x_{jbk}}} } = 1,\;\;\;\;j = 1,\cdots,n $ | (2) |
| $ \sum\limits_{j = 1}^n {{s_j}} {x_{jbk}} \le B,\;\;\;\;b \le n;\;k = 1,\cdots,m $ | (3) |
| $ P{T_{bk}} \ge {p_j}{x_{jbk}},\;\;\;\;j = 1,\cdots,n;b \le n;\;k = 1,\cdots,m $ | (4) |
| $ C{T_{bk}} = C{T_{b - 1,k}} + P{T_{bk}},\;\;\;\;b \le n;\;k = 1,\cdots,m $ | (5) |
| $ {C_{\max }} \ge C{T_{bk}},\;\;\;\;b \le n;\;k = 1,\cdots,m $ | (6) |
| $ {x_{jbk}} = \{ 0,\;1\} ,\;\;\;\;j = 1,\cdots,n;\;b \le \;n;\;k = 1,\cdots,m $ | (7) |
式(1)为优化目标; 式(2)保证一个工件只能分配在一个批中只能在一个机器上加工; 式(3)保证批的容量不超过机器的容量限制; 式(4)说明批的加工时间为批中最长加工时间; 式(5)表明前后批完工时间之间的关系; 式(6)为Cmax的计算方法; 式(7)是对变量xjbk的取值约束.
1.2 问题下界为了能更有效评估后续算法中解的质量, 我们考虑这样一个下界: 假设存在某种单位工件ej具有单位尺寸单位工时, 一个尺寸为sj、加工时间为pj的普通工件可表示为sj*pj个ej, 此时问题转化成若干个性质相同的单位工件的并行机调度问题. 理想状态下所有单位工件能完美分配到批中, 即批中所有工件尺寸之和恰好等于批的容量, 然后均匀分配到各台机器上加工, 可得:
| $ LB\; = \;\sum\limits_{i = 1}^n {{s_i}{p_i}} /(m*B) $ |
显然这样计算得出的结果是一个有效的下界, 其中批的利用率达到最高.
2 分布式估计算法在考虑差异工件的并行批处理机调度中的应用 2.1 分布式估计算法分布式估计算法是一种基于概率模型的进化算法, 最早于1996年由Mühlenbein, Bendisch[19]等人提出, 是当前国际进化计算领域的研究热点. 根据变量之间的相关性, 算法可分为三类: 变量无关、双变量相关和多变量相关; 按照变量的类型可分为离散变量的分布式估计算法和连续域上的分布式估计算法.
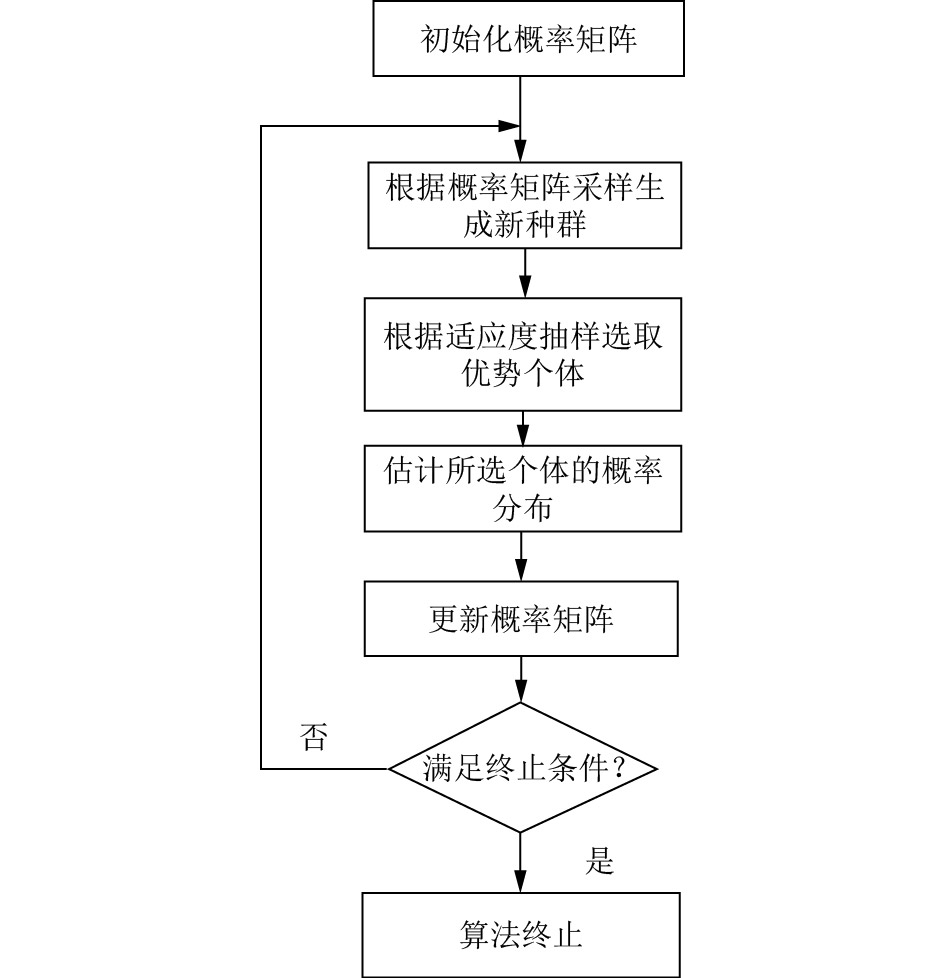
分布式估计算法不同于经典的遗传算法, 它摒弃了遗传算法中采用选择、交叉、变异的方式生成子代种群的策略, 转而采用概率模型来更新下一代种群, 通过收集统计全局信息, 学习优势个体特征来更新概率模型进行采样, 然后生成新的个体. 该算法基本流程如图1所示.
2.2 编码与解码论文采用基于工件序列的编码方式, 每个工件有相应的序列编号, 根据不同的排列可得到不同的调度方案.
|
图 1 EDA基本流程图 |
给定一个工件序列, 首先我们采用FF (First-Fit)规则进行分批, 然后根据LPT (Longerst Processing Time)方法选择当前处于空闲状态的机器进行调度. FF规则如下:
步骤1: 选择工件序列中第一个工件加入到当前批中, 若违反机器容量约束, 考虑下一个工件;
步骤2: 每当工件完成分批, 则从序列中去除该工件; 若当前批容量已满或不能容纳其它任何工件, 则新建一个批;
步骤3: 重复步骤1~2, 直到所有工件完成分批;
分批完成后, 按批次的加工时间由长到短重新排列, 并根据此排列顺序选择非加工状态的机器进行加工, 若存在多台非加工状态的机器, 则任选其中之一进行加工.
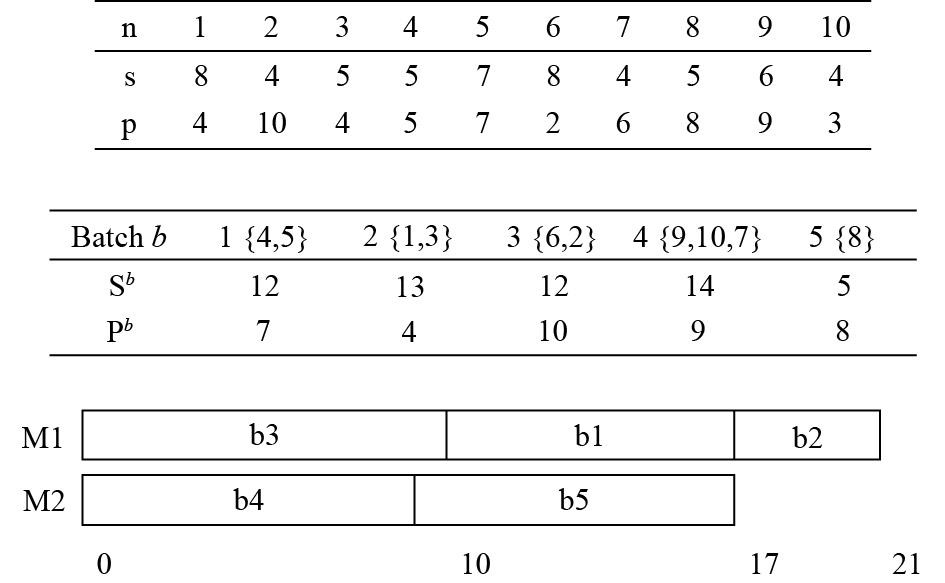
考虑10个工件在两台机器上加工, 假设各台机器容量均为15, 工件序列为[4, 5,1,3,6,2,9,10,7,8], 工件属性及分批调度结果如图2所示.
2.3 概率模型与更新机制算法采用概率矩阵P来表征分布估计模型, Pij(t)表示第t代中工件i出现在位置j周围的概率, 这里用“周围”是因为我们考虑了几种不同的更新策略来计算工件i在位置j左右的概率,而不是仅仅在固定位置j上.
|
图 2 10工件调度示意图 |
| $ {{{P}}_{ij}}(t)\; = \;\left\{ {\begin{array}{*{20}{l}} {{p_{11}}(t)}& \cdots &{{p_{1n}}(t)}\\ {\;\; \vdots }& \ddots &{\;\; \vdots }\\ {{p_{n1}}(t)}& \cdots &{{p_{nn}}(t)} \end{array}} \right\} $ |
算法初始阶段所有概率值均设为1/n, 以保证工件能被均匀抽样. 对于每一代种群, 设种群规模为Q, 我们根据个体的Cmax值计算适应度值(fitness), 然后挑选最优SP_Size个个体估计其概率分布, 通过对其学习来更新概率矩阵. 这里的fitness及SP_Size计算如下:
| $ \begin{array}{l} fitness(i)\; = \;1.1\;*\max \{ {C_{\max }}(1),\cdots,{C_{\max }}(Q)\} \;{\rm{ - }}\;{C_{\max }}(i);\\ SP\_Size\;{\rm{ = }}\;\alpha \;{\rm{*}}\;Q \end{array} $ |
其中, α为优势个体选择比例, 0<α<1.
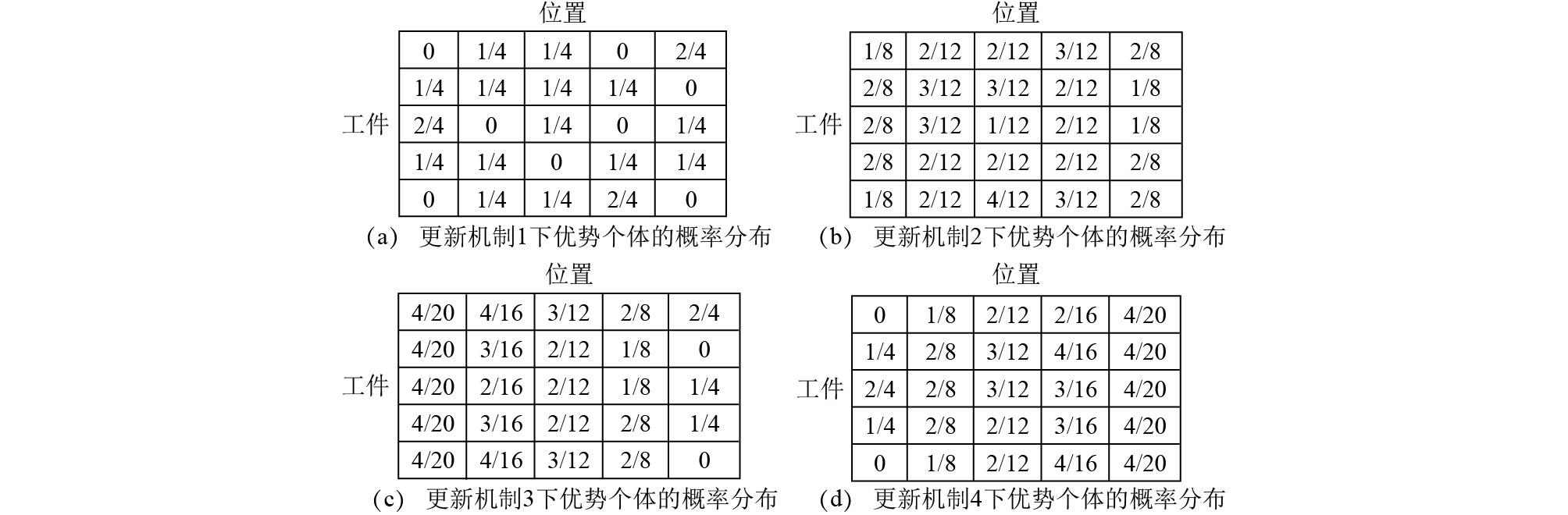
论文中采用FF-LPT规则解码, 因此工件的位置对于批的形成有很大影响, 相邻位置的工件就越有可能分配到同一个批中. 我们考虑4种更新机制来完善概率矩阵, 第一种更新机制学习优势个体中当前位置工件的概率分布; 第二种更新机制学习当前位置及其之前位置工件的概率分布; 第三种更新机制与第二种相反, 通过学习优势个体中当前位置及其之后位置工件的概率分布; 第四种更新机制考虑当前位置及其邻域内工件的概率分布. 具体更新方式如下:
| $ \begin{split} (1)\;&{p_{ij}}(t + 1) = (1 - \beta ){p_{ij}}(t) + \dfrac{\beta }{{SP\_Size}}\displaystyle\sum\limits_{k = 1}^{SP\_Size} {I_{ij}^k} \quad\quad\quad\quad\;\\ &I_{ij}^k = \left\{ \begin{array}{*{20}{l}} {1,\;\;\;\;\;\;\;\;if\text{工件}i\;\text{放在位置}j\;\text{上}}\\ {0,\;\;\;\;\;\;\;\;{\rm{otherwise}}} \end{array}\right. \end{split} $ |
| $ \begin{split} (2)\;&{p_{ij}}(t + 1) = (1 - \beta ){p_{ij}}(t) + \dfrac{\beta }{{j*SP\_Size}}\displaystyle\sum\limits_{k = 1}^{SP\_Size} {I_{ij}^k}\quad\;\;\;\;\;\quad \\ &I_{ij}^k = \left\{ \begin{array}{*{20}{l}} {1,\;\;\;\;\;\;\;if\text{工件}i\;\text{放在位置}j\;\text{或之前位置}}\\ {0,\;\;\;\;\;\;{\rm{otherwise}}} \end{array}\right. \end{split} $ |
| $ \begin{split} (3)\;&{p_{ij}}\left( {t + 1} \right) = \left( {1 - \beta } \right){p_{ij}}\left( t \right) + \dfrac{\beta }{{\left( {n - j + 1} \right)*SP\_Size}}\displaystyle\sum\limits_{k = 1}^{SP\_Size} {I_{ij}^k}\\ &I_{ij}^k = \left\{ \begin{array}{*{20}{l}} {1,\;\;\;\;\;\;\;\;if\text{工件}i\;\text{放在位置}j\;\text{或之后位置}}\\ {0,\;\;\;\;\;\;\;{\rm{otherwise}}} \end{array}\right. \end{split} $ |
| $ \begin{split} (4)\;&{p_{ij}}(t + 1) = (1 - \beta ){p_{ij}}(t) + \dfrac{\beta }{{SP\_Size}}\displaystyle\sum\limits_{k = 1}^{SP\_Size} {\dfrac{{I_{ij}^k}}{{{\rm{|}}{v_j}{\rm{|}}}}} \quad\quad\quad\quad\\ &I_{ij}^k = \left\{ \begin{array}{*{20}{l}} {1,\;\;\;\;\;\;\;if\text{工件}i\;\text{放在位置}j\;\text{邻域范围内},}\\ \;\;\;\;\;\;\;\;\;\;{\text{邻域大小为}{\rm{|}}{v_j}{\rm{|}}}\\ {0,\;\;\;\;\;\;{\rm{otherwise}}} \end{array}\right. \end{split} $ |
其中, β为学习率, 0<β<1;vj为单边邻域大小, 例如当vj= 2时, 位置5的邻域为位置3, 4, 5, 6, 7, |v5|为5; 位置1的邻域为位置1, 2, 3, |v1|为3.
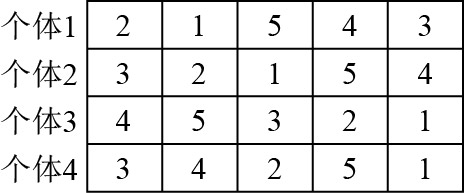
为了阐明概率矩阵更新过程, 我们用一个包含5个工件的算例示范. 假设挑选4个优势个体, 如图3所示. 设vj为1, 根据4种更新机制统计各个位置的工件信息, 构建优势个体的概率分布矩阵, 结果如图4所示. 通过学习优势个体的概率分布特征来更新概率矩阵P, 然后基于比例选择采用轮盘赌的方式依次决定各个位置上工件编号, 即可获得新的个体.
|
图 3 挑选的4个优势个体 |
2.4 面向差异工件的并行批处理机调度问题的分布式估计算法
综上, 面向差异工件的并行批处理机调度问题的分布式估计算法如算法1所示.
算法1. 面向差异工件的并行批处理机调度问题的分布式估计算法
初始化参数Q, α, β, gen(迭代次数), 随机生成初始种群;
t = 0 ;
While t < gen
采用FF-LPT规则对种群中个体进行解码, 计算适应度值;
根据适应度值选取最优的SP_Size个个体, 并估计其概率分布;
选取2.3中的更新策略对概率矩阵进行更新;
根据新的概率矩阵采样生成新的种群;
令t = t+1;
end
输出最优调度方案及makespan.
3 实验设计与结果分析 3.1 实验设计本实验根据文献[9]提出的方法生成随机算例, 算例规模按3个标准划分: 工件数量n, 工件尺寸s, 加工时间p; 其中s、p均服从离散均匀分布; 机器数量m为2或4, 容量均为20. 具体参数见表1.
每类算例提供一个编号. 例如包含50个工件, 工件尺寸服从[1, 10]分布, 加工时间满足[1, 20], 在两台机器上加工的一类算例编号为J2S3P2M1. 每类算例随机生成10个子算例, 每个算例计算10次.
|
图 4 不同更新机制下优势个体概率矩阵计算结果 |
| 表 1 算例规模 |
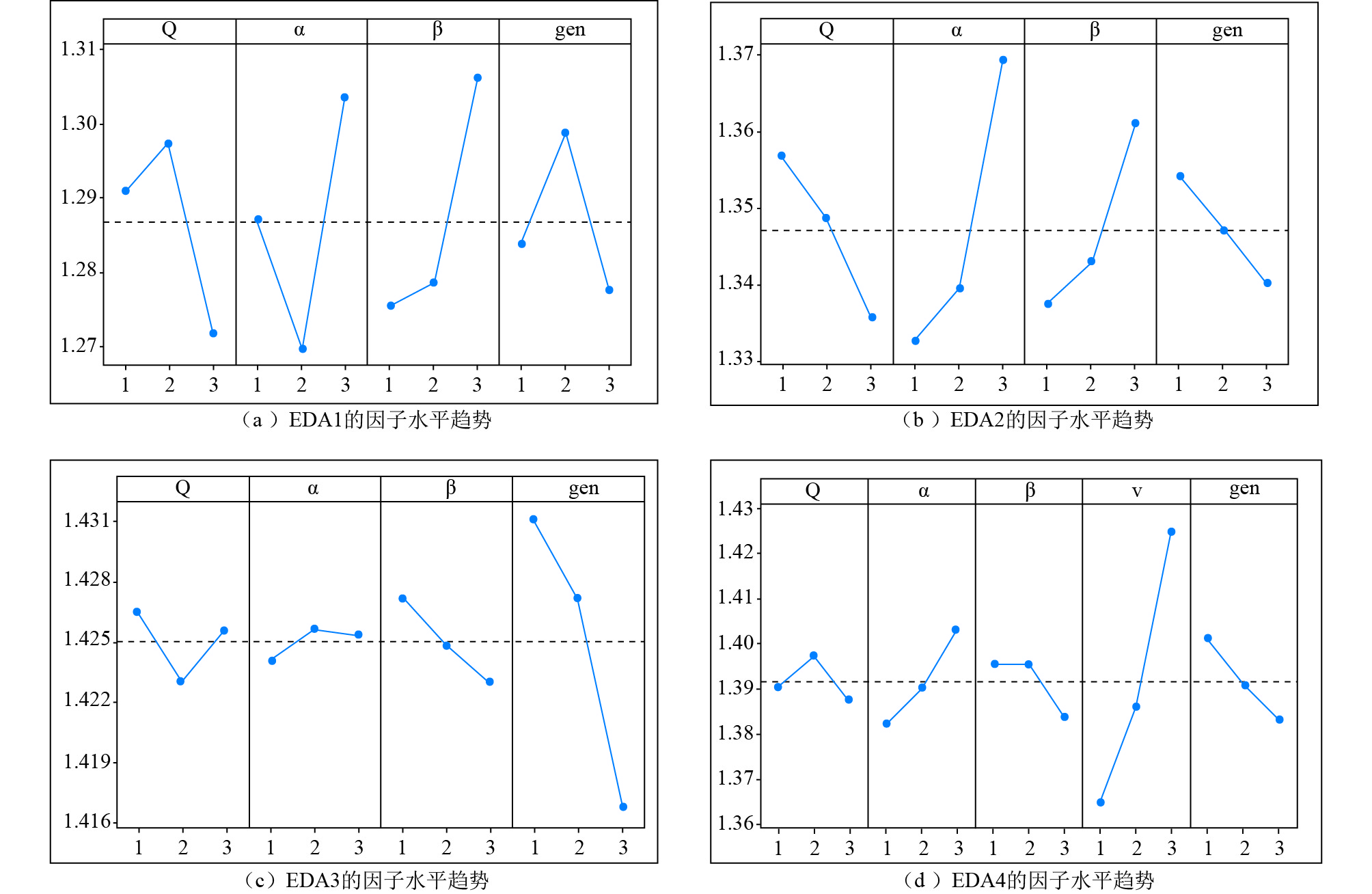
影响EDA性能的参数主要有4个: Q, α, β, gen. 其中, 优势个体的选择比例 α对概率矩阵的更新有很大影响, 若比例选择过小, 子代种群与当代个体相似度较高, 则容易陷入局部最优; 若比例选择过大, 个体的优势特征弱化, 导致概率矩阵的学习效果差. 为此, 论文考虑3种不同的 α值进行预实验. 为了选取合适的参数值展开后续实验, 我们采用田口方法对不同水平的参数进行评估, 将参数作为因子, 并对每个因子设置3水平的参考值, 具体的参数设置见表2 .
| 表 2 参数设置 |
算法提供了4种更新策略, 为方便表述, 依次记为EDA1, EDA2, EDA3, EDA4, 其中EDA3表示采取第三种更新策略. 由于EDA4中需要考虑单边邻域v, 因此为EDA4单独设立5因素3水平的实验, 参数顺序为Q, α, β, v, gen. v具有3水平, 分别是[2,3,5], 其余因素同表2 .
根据实验参数和因子水平,选取正交阵列L9(34)和L27(35), 其中L9(34)表示针对3因素4水平的问题设计9种实验. 我们针对50规模的工件, 生成12(3×2×2) 个算例, 每个算例采取9次试验, 算5次, 一共计算12×9×5次; 对于EDA4, 需要计算12×27×5次. 最后的平均响应变量值(ARV)计算方式如下:
| $ {\rm{ARV}} = \dfrac{{\displaystyle\sum\limits_{i = 1}^n {{C_{\max }}(i)/LB(i)} }}{n} $ |
其中, n为算例个数. 显然, ARV越小越好.
图5中各子图横坐标为因子水平值, 纵坐标为ARV, 分析可知, EDA1最优参数组合为: Q=60, α=0.2, β=0.1, gen=500; EDA2最优组合为: Q=60, α=0.1, β=0.1, gen=500; EDA3最优组合为:Q=50, α=0.1, β=0.3, gen=500; EDA4最优组合为: Q=60, α=0.1, β=0.3, ν=2, gen=500.
3.2 实验结果及分析为了评估算法的性能, 我们将和文献[9]提出的模拟退火算法(SA) 以及经典的遗传算法(GA)作对比. SA中各项参数与原文献一致, GA中种群规模和迭代次数同EDA一样, 变异概率设为0.1. 所有的算法均由Matlab实现, 实验环境为4核3.4 GHz、8 GB RAM的Windows10系统.
表3、表4分别给出了2台和4台机器环境下所有算例的结果. 实验中分别统计了各个算法运行得到的最优值、平均值、最差值及运行时间等, 这里只给出了比值ratio,计算公式为:
| $ ratio\;{\rm{ = }}\;ave({C_{\max }})/LB $ |
ratio越小, 说明结果越接近下界, 所得到的解越接近最优解.
|
图 5 不同更新机制下EDA的因子水平趋势 |
从表3、表4中可以看出, 对于绝大部分算例, 我们提出的4种EDA得到的解均是要优于SA算法的. 对于2台机器, EDA1的ratio均值为1.24, GA为1.27, SA为1.44. 随着工件规模的增加, 算法的解的质量也越来越好, 尤其是在较多并行机的情况下.
值得注意的是, 4种EDA算法中, EDA1的性能是最好的, 其次是EDA2, EDA3的性能最差. EDA2与EDA3的更新机制是截然相反的, EDA3考虑当前位置及其之后位置工件的概率, 但是由于采样时我们是按照顺位比例选择的方式依次决定各个位置的工件, 这导致EDA3效率较低. 而EDA1只考虑当前位置的工件的概率分布, 使得概率分布极为“精纯”, 所以性能较好.
另外, GA的性能比想象中好很多, 对于小规模算例, GA的解甚至比EDA1还要占优; 但对于大规模工件, EDA1得到的解的质量要优于GA.
| 表 3 M1类算例结果 |
| 表 4 M2类算例结果 |
运行时间方面, 4种EDA均是要长于GA、SA的. 这是由于EDA生成下一代种群需要反复对概率矩阵采样生成新的个体, 这一过程相对于SA中邻域搜索或GA中交叉、变异要繁杂很多,因此造成时间上的冗余.
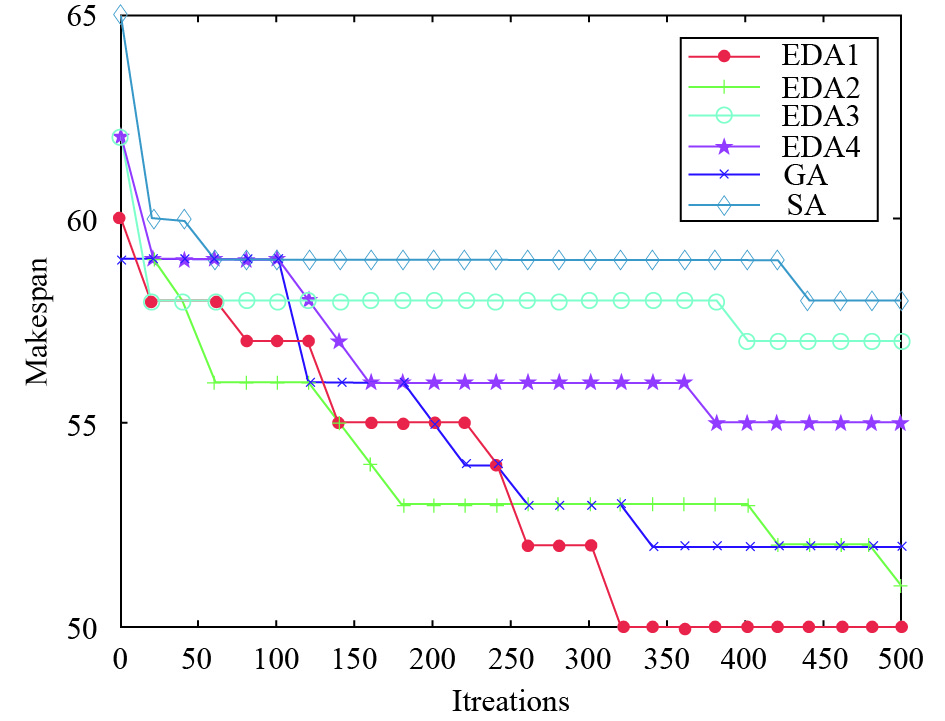
图6给出了J2S2P1M1类典型算例的收敛趋势图. 从中可以看出EDA1的收敛性更好. 其他类算例的收敛趋势与此类似.
|
图 6 J2S2P1M1类典型算例收敛趋势图 |
4 结论与展望
本文研究了分布式估计算法在考虑差异工件的并行批处理机调度中的应用问题. 首先提出了一个混合整数规划模型和一个下界, 然后采用FF-LPT规则实现对工件的分批和排序; 对于基于概率矩阵的分布式估算法, 提出了4种不同的更新机制, 并通过仿真实验和SA、GA对比, 验证了算法的有效性. 经比较知, 对于采取不同更新机制的EDA, EDA1的性能最好, EDA2次之, EDA3性能最差.
未来的研究可考虑通过局部优化来进一步优化算法的性能, 以及考虑多阶段并行机调度问题或不同的优化目标等.
| [1] |
Uzsoy R, Lee CY, Martin-Vega LA. A review of production planning and scheduling models in the semiconductor industry part Ⅱ: Shop-floor control. IIE Transactions, 1994, 26(5): 44-55. DOI:10.1080/07408179408966627 |
| [2] |
Ghazvini FJ, Dupont L. Minimizing mean flow times criteria on a single batch processing machine with non-identical jobs sizes. International Journal of Production Economics, 1998, 55(3): 273-280. DOI:10.1016/S0925-5273(98)00067-X |
| [3] |
Melouk S, Damodaran P, Chang PY. Minimizing makespan for single machine batch processing with non-identical job sizes using simulated annealing. International Journal of Production Economics, 2004, 87(2): 141-147. DOI:10.1016/S0925-5273(03)00092-6 |
| [4] |
周盛超. 差异工件机器批调度若干问题研究[博士学位论文]. 合肥: 中国科学技术大学, 2016.
|
| [5] |
Ikura Y, Gimple M. Efficient scheduling algorithms for a single batch processing machine. Operations Research Letters, 1986, 5(2): 61-65. DOI:10.1016/0167-6377(86)90104-5 |
| [6] |
Lee CY, Uzsoy R, Martin-Vega LA. Efficient algorithms for scheduling semiconductor burn-in operations. Operations Research, 1992, 40(4): 764-775. DOI:10.1287/opre.40.4.764 |
| [7] |
Uzsoy R. Scheduling a single batch processing machine with non-identical job sizes. International Journal of Production Research, 1994, 32(7): 1615-1635. DOI:10.1080/00207549408957026 |
| [8] |
Zhou SC, Chen HP, Xu R, et al. Minimising makespan on a single batch processing machine with dynamic job arrivals and non-identical job sizes. International Journal of Production Research, 2014, 52(8): 2258-2274. DOI:10.1080/00207543.2013.854937 |
| [9] |
Chang PY, Damodaran P, Melouk S. Minimizing makespan on parallel batch processing machines. International Journal of Production Research, 2004, 42(19): 4211-4220. DOI:10.1080/00207540410001711863 |
| [10] |
Damodaran P, Chang PY. Heuristics to minimize makespan of parallel batch processing machines. The International Journal of Advanced Manufacturing Technology, 2008, 37(9–10): 1005-1013. |
| [11] |
Chen HP, Du B, Huang GQ. Metaheuristics to minimise makespan on parallel batch processing machines with dynamic job arrivals. International Journal of Computer Integrated Manufacturing, 2010, 23(10): 942-956. DOI:10.1080/0951192X.2010.495137 |
| [12] |
Xu R, Chen HP, Li XP. Makespan minimization on single batch-processing machine via ant colony optimization. Computers & Operations Research, 2012, 39(3): 582-593. |
| [13] |
Xu SB, Bean JC. A genetic algorithm for scheduling parallel non-identical batch processing machines. Proceedings of 2007 IEEE Symposium on Computational Intelligence in Scheduling. Honolulu, HI, USA. 2007. 143–150.
|
| [14] |
Damodaran P, Diyadawagamage DA, Ghrayeb O, et al. A particle swarm optimization algorithm for minimizing makespan of nonidentical parallel batch processing machines. The International Journal of Advanced Manufacturing Technology, 2012, 58(9–12): 1131-1140. |
| [15] |
Zhou SC, Liu M, Chen HP, et al. An effective discrete differential evolution algorithm for scheduling uniform parallel batch processing machines with non-identical capacities and arbitrary job sizes. International Journal of Production Economics, 2016, 179: 1-11. DOI:10.1016/j.ijpe.2016.05.014 |
| [16] |
Zhou SC, Li XP, Chen HP, et al. Minimizing makespan in a no-wait flowshop with two batch processing machines using estimation of distribution algorithm. International Journal of Production Research, 2016, 54(16): 4919-4937. DOI:10.1080/00207543.2016.1140920 |
| [17] |
Aickelin U, Burke EK, Li J. An estimation of distribution algorithm with intelligent local search for rule-based nurse rostering. Journal of the Operational Research Society, 2007, 58(12): 1574-1585. DOI:10.1057/palgrave.jors.2602308 |
| [18] |
Pinedo ML. Scheduling: Theory, Algorithms, and Systems. 5th ed. Cham: Springer, 2016.
|
| [19] |
Mühlenbein H, Paaß G. From recombination of genes to the estimation of distributions I. Binary parameters. Proceedings of the 4th International Conference on Parallel Problem Solving from Nature. Berlin, Germany. 1996. 178–187.
|
 2019, Vol. 28
2019, Vol. 28



